A Generalized Loss Function for Crowd Counting and Localization阅读笔记
简单来说,就是用了UOT来解决人群计数问题
代码:https://github.com/jia-wan/GeneralizedLoss-Counting-Pytorch.git
我改了一点的:https://github.com/Nightmare4214/GeneralizedLoss-Counting-Pytorch.git
loss
设density map为 A = { ( a i , x i ) } i = 1 n \mathcal{A} =\left\{\left(a_i, \mathbf{x}_i\right)\right\}_{i=1}^{n} A={(ai,xi)}i=1n
其中 a i a_i ai为预测density, x i ∈ R n \mathbf{x}_i\in\mathbb{R}^n xi∈Rn为坐标, n n n为像素个数
令 a = [ a i ] i \mathbf{a} = \left[a_i\right]_i a=[ai]i,也就是density map转成列向量
真实点图为 B = { ( b j , y j ) } j = 1 m \mathcal{B}=\left\{\left(b_j,\mathbb{y}_j\right)\right\}_{j=1}^m B={(bj,yj)}j=1m
其中 y j \mathbf{y}_j yj为坐标, m m m为标注点个数, b j b_j bj为这个点代表的人群数量
这个论文假设 b = [ b j ] j = 1 m \mathbf{b}=\left[b_j\right]_j = \mathbf{1}_m b=[bj]j=1m,也就是说每个点只有一个人
熵正则化的UOT为
L C τ ( A , B ) = min P ∈ R + n × m ⟨ C , P ⟩ − ϵ H ( P ) + τ D 1 ( P 1 m ∣ a ) + τ D 2 ( P T 1 n ∣ b ) \mathcal{L}_{\mathbf{C}}^{\tau}\left(\mathcal{A},\mathcal{B}\right) = \min_{\mathbf{P}\in\mathbb{R}_+^{n\times m}} \left\langle \mathbf{C},\mathbf{P}\right\rangle -\epsilon H\left(\mathbf{P}\right) + \tau D_1\left(\mathbf{P}\mathbf{1}_m|\mathbf{a}\right) +\tau D_2\left(\mathbf{P}^T\mathbf{1}_n|\mathbf{b}\right) LCτ(A,B)=P∈R+n×mmin⟨C,P⟩−ϵH(P)+τD1(P1m∣a)+τD2(PT1n∣b)
其中 C ∈ R + n × m \mathbf{C}\in\mathbb{R}_+^{n\times m} C∈R+n×m是传输代价矩阵, C i , j C_{i,j} Ci,j为将density从 x i \mathbf{x}_i xi搬运到 y j \mathbf{y}_j yj的距离
P \mathbf{P} P为传输矩阵
令 a ^ = P 1 m , b ^ = P T 1 n \hat{\mathbf{a}} = \mathbf{P}\mathbf{1}_m, \hat{\mathbf{b}}=\mathbf{P}^T\mathbf{1}_n a^=P1m,b^=PT1n
这个loss有4个部分
第一部分是传输的loss,目的是将预测的density map往真实标注靠
第二部分是熵 H ( P ) = − ∑ i , j P i , j log P i , j H\left(\mathbf{P}\right) = -\sum_{i,j}P_{i,j}\log P_{i,j} H(P)=−∑i,jPi,jlogPi,j是熵正则化项,用来控制稀疏程度,越大越稀疏(会趋于均匀分布),反之亦然
第三部分就是希望 a ^ \hat{\mathbf{a}} a^靠近 a \mathbf{a} a
第四部分就是希望 b ^ \hat{\mathbf{b}} b^靠近 b \mathbf{b} b
论文里, D 1 D_1 D1取 L 2 L_2 L2的平方
D 2 D_2 D2取 L 1 L_1 L1
代价矩阵
C i , j = e 1 η ( x i , y j ) ∥ x i − y j ∥ 2 C_{i,j} = e^{\frac{1}{\eta\left(x_i,y_j\right)}\|\mathbf{x}_i-\mathbf{y}_j\|_2} Ci,j=eη(xi,yj)1∥xi−yj∥2
这里的 x i , y j \mathbf{x}_i,\mathbf{y}_j xi,yj是经过归一化的
不过要注意,代码里这个 η ( x i , y j ) \eta\left(x_i,y_j\right) η(xi,yj)是常数,默认是 0.6 0.6 0.6
求解
采用的是sinkhorn
P = diag ( u ) K diag ( v ) , K = exp ( − C / ε ) \mathbf{P}=\operatorname{diag}(\mathbf{u}) \mathbf{K} \operatorname{diag}(\mathbf{v}), \quad \mathbf{K}=\exp (-\mathbf{C} / \varepsilon) P=diag(u)Kdiag(v),K=exp(−C/ε)
这里近似 D 1 , D 2 D_1,D_2 D1,D2为KL散度,这样的话有高效的解法
u ( ℓ + 1 ) = ( a K v ( ℓ ) ) τ τ + ϵ , v ( ℓ + 1 ) = ( b K ⊤ u ( ℓ + 1 ) ) τ τ + ϵ \mathbf{u}^{(\ell+1)}=\left(\frac{\boldsymbol{a}}{\mathbf{K} \mathbf{v}^{(\ell)}}\right)^{\frac{\tau}{\tau+\epsilon}}, \quad \mathbf{v}^{(\ell+1)}=\left(\frac{\boldsymbol{b}}{\mathbf{K}^{\top} \mathbf{u}^{(\ell+1)}}\right)^{\frac{\tau}{\tau+\epsilon}} u(ℓ+1)=(Kv(ℓ)a)τ+ϵτ,v(ℓ+1)=(K⊤u(ℓ+1)b)τ+ϵτ
(其实即使是 K L KL KL散度,他代码似乎也不能这么写)
代码
数据集
预处理
用的是UCF-QNRF
预处理:
1.让 h , w h,w h,w中较小的那个,处于 [ 512 , 2048 ] \left[512,2048\right] [512,2048]的范围,另一个按照缩放比例调整
2.过滤不在图片中的点
3.额外计算每个点到其他点的一个距离,具体地
P = ( p 1 T p 2 T ⋮ p m T ) , p i ∈ R 2 \mathbf{P} = \begin{pmatrix} \mathbf{p}_1^T\\ \mathbf{p}_2^T\\ \vdots\\ \mathbf{p}_m^T \end{pmatrix},\quad \mathbf{p}_i\in\mathbb{R}^2 P= p1Tp2T⋮pmT ,pi∈R2
d i s = [ ∥ p i − p j ∥ ] i , j \mathbf{dis} = \left[\|\mathbf{p}_i-\mathbf{p}_j\|\right]_{i,j} dis=[∥pi−pj∥]i,j
最后对每一行进行快排的那个选择哨兵的过程,找到第3个(从0开始数)
对第 1 , 2 , 3 1,2,3 1,2,3个元素取平均(从0开始数)
def find_dis(point):a = point[:, None, :]b = point[None, ...]dis = np.linalg.norm(a - b, ord=2, axis=-1) # dis_{i,j} = ||p_i - p_j||# mean(4th_min, 2 of the [1st_min, 2nd_min, 3rd_min])dis = np.mean(np.partition(dis, 3, axis=1)[:, 1:4], axis=1, keepdims=True)return dis
因此得到的标签为
P = [ ( x i , y i , d i s i ) ] i ∈ R m × 3 \mathbf{P}=\left[\left(x_i,y_i,dis_i\right)\right]_i\in\mathbb{R}^{m\times 3} P=[(xi,yi,disi)]i∈Rm×3
读取数据
随机裁剪图片,到 ( 512 , 512 ) \left(512,512\right) (512,512)
设 i , j i,j i,j为裁剪的左上角坐标, h = w = 512 h=w=512 h=w=512
接着读取标签
根据 d i s dis dis来设定一个小矩形
计算这个矩形在裁剪范围的面积,和矩形面积的 1 4 \frac{1}{4} 41
如果这个比例大于0.3,就选择这个点,否则舍弃
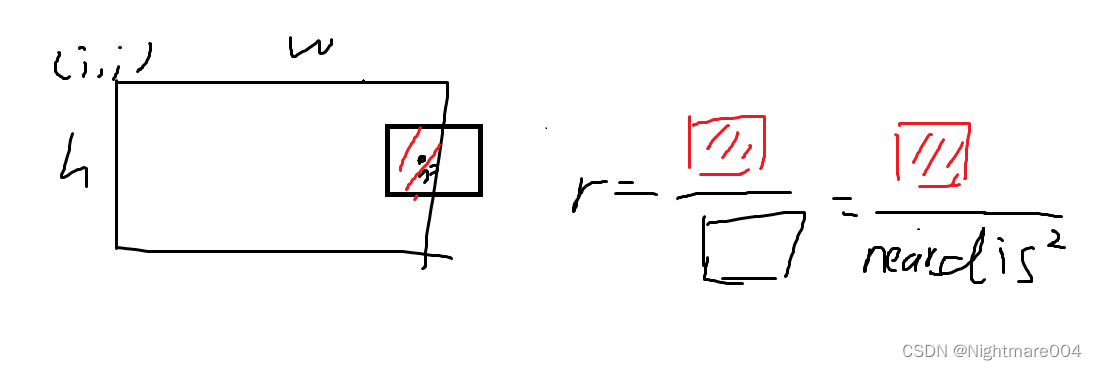
然后其他的就是随机水平翻转
模型
vgg19+上采样+两层卷积+abs
训练
注意这里sinkhorn是有 ϵ − scaling heuristic \epsilon-\text{scaling heuristic} ϵ−scaling heuristic的这样可以做到20轮以内收敛
为了数值稳定,还用了 log-domain \text{log-domain} log-domain
结果
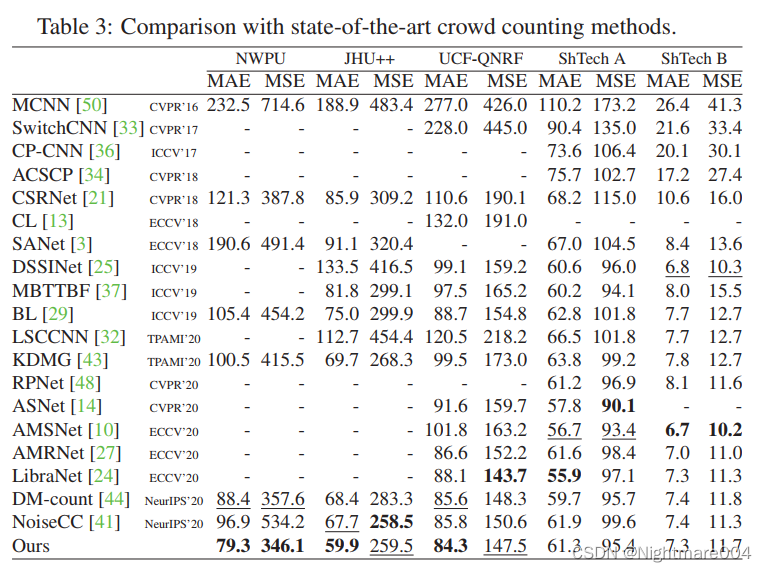
作者的提供的模型的结果:mae 85.09911092883813, mse 150.88815648865386
我在UCF-QNRF跑的结果:mae:85.69232401590861, mse:155.30853159819492
相关文章:

A Generalized Loss Function for Crowd Counting and Localization阅读笔记
简单来说,就是用了UOT来解决人群计数问题 代码:https://github.com/jia-wan/GeneralizedLoss-Counting-Pytorch.git 我改了一点的:https://github.com/Nightmare4214/GeneralizedLoss-Counting-Pytorch.git loss 设density map为 A { ( a…...

SocketD协议单链接双向RPC模式怎么实现
SocketD是一个基于Socket的通信框架,支持单链接双向RPC模式。在实现单链接双向RPC模式时,需要按照一定的协议进行通信,以下是一个简单的实现示例: 定义通信协议:首先,需要定义客户端和服务端之间的通信协议…...

apache poi 设置背景颜色
apache poi 设置背景颜色 要设置 Apache POI 中 HSSFCellStyle 的背景颜色,你可以按照以下步骤进行操作: 首先,创建一个 HSSFWorkbook 对象来表示你的 Excel 工作簿: HSSFWorkbook workbook new HSSFWorkbook();然后ÿ…...

Vue2-Vue3组件间通信-EventBus方式-函数封装
Vue3中采用EventBus方式进行组件间通信与Vue2有一定区别 1.创建EventBus 在Vue2中,我们可以在main.js中创建一个全局的EventBus,代码如下: // EventBus.js import Vue from vue const EventBus new Vue() export default EventBus// main.…...

【SpringBoot】| SpringBoot 和 web组件
目录 一:SpringBoot 和 web组件 1. SpringBoot中使用拦截器(重点) 2. SpringBoot中使用Servlet 3. SpringBoot中使用过滤器(重点) 4. 字符集过滤器的应用 一:SpringBoot 和 web组件 1. SpringBoot中使…...
dflow工作流使用1——架构和基本概念
对于容器技术、工作流等概念完全不懂的情况下理解dflow的工作方式会很吃力,这里记录一下个人理解。 dflow涉及的基本概念 工作流的概念很好理解,即某个项目可以分为多个步骤,每个步骤可以实现独立运行,只保留输入输出接口&#x…...
python小游戏课程设计报告,python游戏课程设计报告
大家好,给大家分享一下python2048游戏课程设计报告,很多人还不知道这一点。下面详细解释一下。现在让我们来看看!...
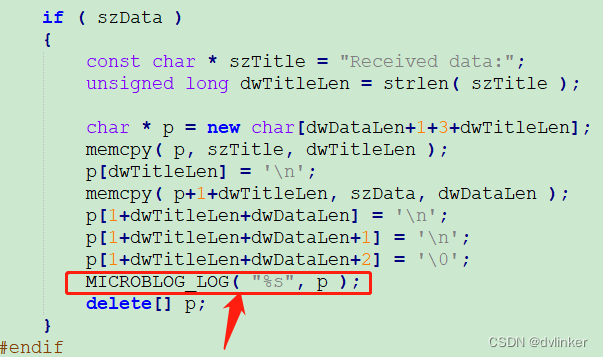
使用Windbg分析从系统应用程序日志中找到的系统自动生成的dump文件去排查问题
目录 1、尝试将Windbg附加到目标进程上进行动态调试,但Windbg并没有捕获到 2、在系统应用程序日志中找到了系统在程序发生异常时自动生成的dump文件 2.1、查看应用程序日志的入口 2.2、在应用程序日志中找到系统自动生成的dump文件 3、使用Windbg静态分析dump文…...

后端技术趋势指南|如何选择自己的技术方向
编程多条路,条条通罗马 后台大佬 后台路线都是面对后台服务器业务,比如web后台服务器,视频后台服务器,搜索后台服务器,游戏后台服务器,直播后台服务器,社交IM后台服务器等等,大部分…...

Delphi XE的原生JSONObject如何判断键值是否存在?
【问题现象】 Delphi XE的原生JSONObject,取出键值的时候如下: //json是传入的参数,里面包括"food_name"等之类的键值,没有food_type键值 procedure XXXXFunciton(json:TJSONObject) var strFoodName,strFoodType:S…...

Go Runtime功能初探
以下内容,是对 运行时 runtime的神奇用法[1] 的学习与记录 目录: 1.获取GOROOT环境变量 2.获取GO的版本号 3.获取本机CPU个数 4.设置最大可同时执行的最大CPU数 5.设置cup profile 记录的速录 6.查看cup profile 下一次堆栈跟踪数据 7.立即执行一次垃圾回收 8.给变量…...
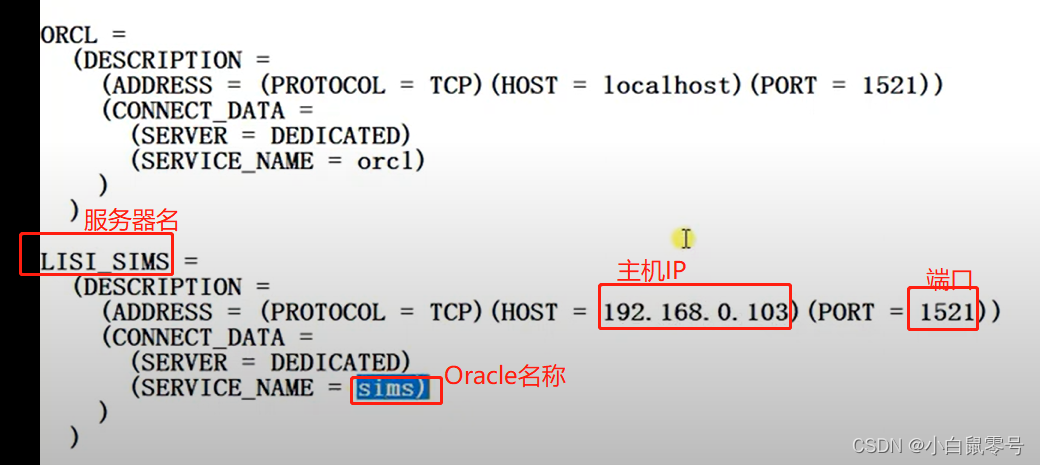
01|Oracle学习(监听程序、管理工具、PL/SQL Developer、本地网络服务介绍)
基础概念 监听程序:运行在Oracle服务器端用于侦听客户端请求的程序。 相当于保安,你来找人,他会拦你,问你找谁。他去帮你叫人过来。 配置监听程序应用场景 Oracle数据库软件安装之后没有监听程序(服务)…...
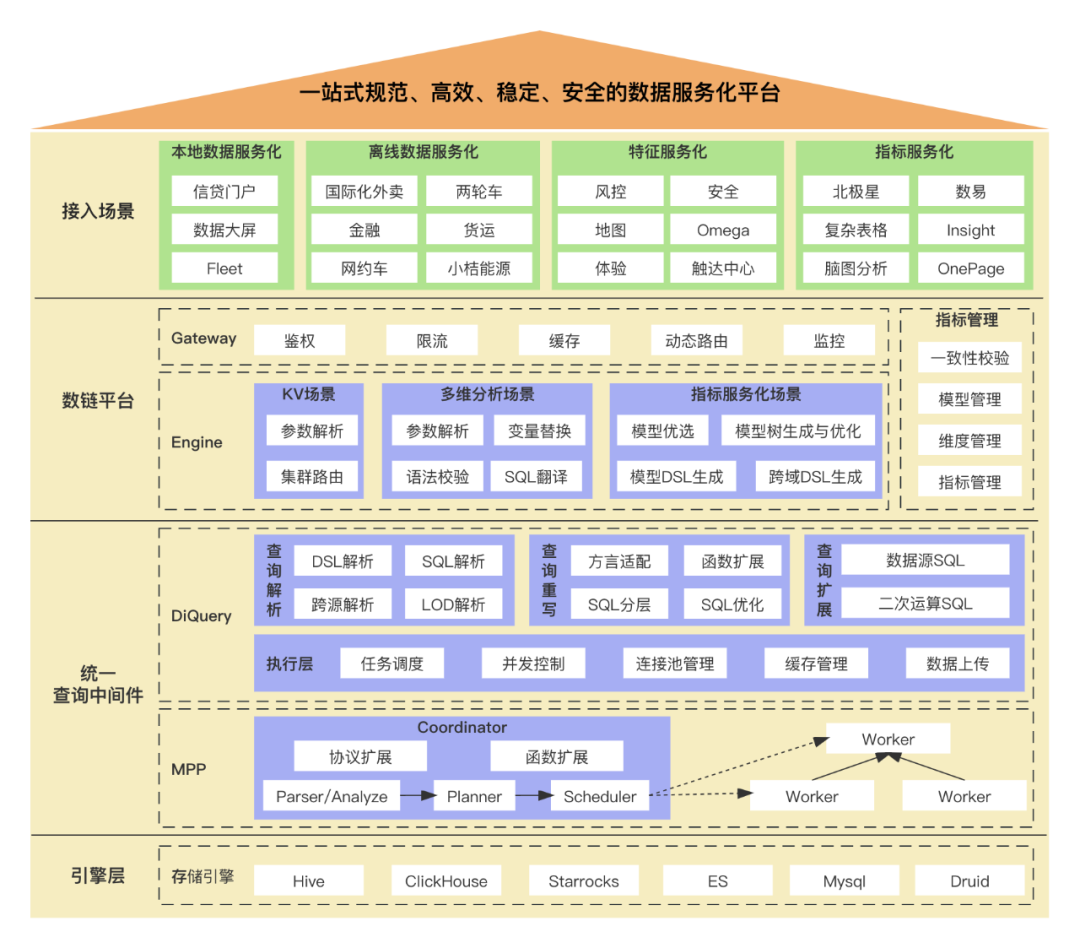
滴滴数据服务体系建设实践
什么是数据服务化 大数据开发的主要流程分为数据集成、数据开发、数据生产和数据回流四个阶段。数据集成打通了业务系统数据进入大数据环境的通道,通常包含周期性导入离线表、实时采集并清洗导入离线表和实时写入对应数据源三种方式,当前滴滴内部同步中心…...

VBA技术资料MF36:VBA_在Excel中排序
【分享成果,随喜正能量】一个人的气质,并不在容颜和身材,而是所经历过的往事,是内在留下的印迹,令人深沉而安谧。所以,优雅是一种阅历的凝聚;淡然是一段人生的沉淀。时间会让一颗灵魂࿰…...

Shell脚本学习3
文章目录 Shell脚本学习3函数函数定义及使用函数参数获取函数返回值 重定向输入输出重定向 其他Here Document/dev/null 文件Shell文件包含获取当前正在执行脚本的绝对路径按特定字符串截取字符串 Shell脚本学习3 函数 函数定义及使用 函数可以让我们将一个复杂功能划分成若…...

代理模式--静态代理和动态代理
1.代理模式 定义:代理模式就是代替对象具备真实对象的功能,并代替真实对象完成相应的操作并且在不改变真实对象源代码的情况下扩展其功能,在某些情况下,⼀个对象不适合或者不能直接引⽤另⼀个对象,⽽代理对象可以在客户…...
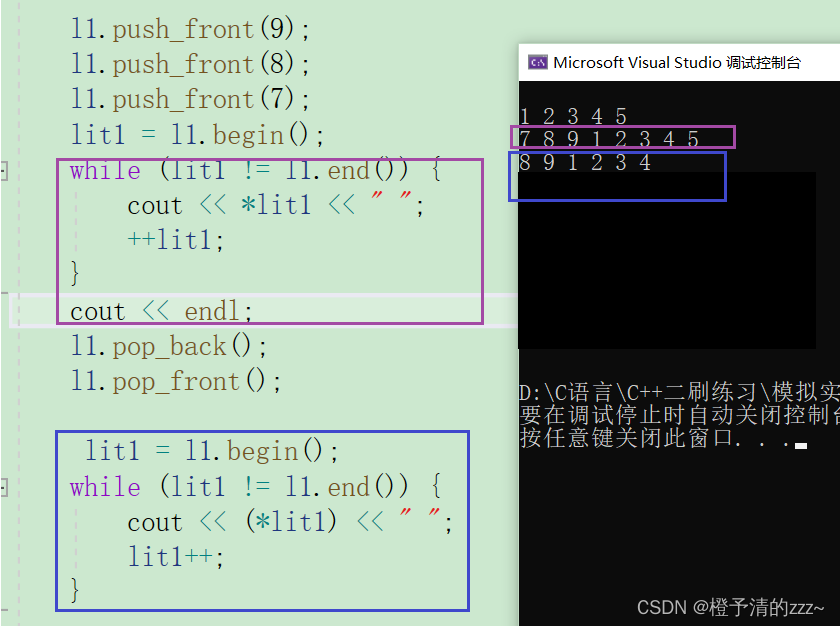
C++容器——list的模拟实现
目录 一.list的基本结构 二. 接下来就是对list类构造函数的设计了: 三.链表数据的增加: 四.接下来就是迭代器的创建了: 四.简单函数的实现: 五.构造与析构 六.拷贝构造和赋值重载 传统写法: 现代写法: 七.迭…...

VUE3 祖孙组件传值调用方法
1.在 Vue 3 中,你可以使用 provide/inject 来实现祖孙组件之间的传值和调用方法。 首先,在祖组件中使用 provide 来提供数据或方法,例如: // 祖组件 import { provide } from vue;export default {setup() {const data Hello;c…...

我的网安之路
机缘 我目前从事网安工作,一转眼我从发布的第一篇文章到现在已经过去了4年了,感慨时间过得很快 曾经我是一名Java开发工程师所以我的第一篇文章是跟开发相关的那个时候还是实习生被安排 一个很难的工作是完成地图实时定位以及根据GPS信息模拟海上追捕,这对刚入职的我来说很难 …...

langchain-ChatGLM源码阅读:webui.py
样式定制 使用gradio设置页面的视觉组件和交互逻辑 import gradio as gr import shutilfrom chains.local_doc_qa import LocalDocQA from configs.model_config import * import nltk import models.shared as shared from models.loader.args import parser from models.load…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
