B. Binary Cafe(二进制的妙用)
题目:Problem - B - Codeforces



总结:
对于该题最简单的方法为使用二进制的数表示状态
例如:
对于一个数7的二进制:111
它的每一位都可表示两种状态我们可以理解为取或者不取
对于7这个数字它可以表示一种状态即在三个位置都取,它们的和为7
对于7(二进制是111)从0(二进制是000)加一来的
每一个数都表示一种状态 过程如下
0(二进制是000)
1(二进制是001)
2(二进制是010)
3(二进制是011)
4(二进制是100)
5(二进制是101)
6(二进制是110)
7(二进制是111)
所以7在二进制中也有另一种理解:
在1 2 4 8 16 32.·······等二进制数组中
子数组之和为7的子数组个数为7+1(这里的加一是空数组的情况)
代码献上(二进制妙用):
#include<iostream>using namespace std;int main()
{int t; cin >> t;while (t--) {int n; //硬币数量int k; //甜品数量cin >> n >> k;k = min(k, 30); //在这里作限制的原因是对于2的30次方远超硬币的数量ncout << min(n + 1, 1 << k) << endl; //前者为花完金币的情况 后者为甜品有限金币花不完}return 0;
}相关文章:

B. Binary Cafe(二进制的妙用)
题目:Problem - B - Codeforces 总结: 对于该题最简单的方法为使用二进制的数表示状态 例如: 对于一个数7的二进制:111 它的每一位都可表示两种状态我们可以理解为取或者不取 对于7这个数字它可以表示一种状态即在三个位置都…...
SpringBoot单元测试
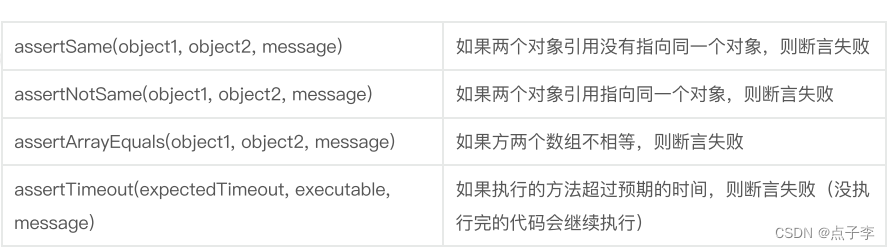
目录 1.什么是单元测试? 2.单元测试有哪些好处? 3.Spring Boot单元测试使⽤ 单元测试的实现步骤 1. ⽣成单元测试类 2. 添加单元测试代码 2.1 .添加Spring Boot框架测试注解:SpringBootTest 2.2 添加单元测试业务逻辑 简单的断⾔说明 1.什么是单元测试? 单元测试(un…...

刷题 41-45
四十一、移除元素 示例 1: 输入:nums [3,2,2,3], val 3 输出:2, nums [2,2] 解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 …...

Centos时间同步
前言 在 Linux 操作系统中,正确的时间同步是非常重要的,因为它对于很多应用程序都是必需的。本文将介绍两种在 Centos 系统中同步当前时间的方式。 方法一:使用 ntpdate 命令同步当前时间 ntpdate 命令是一种简单快捷的同步当前时间的方式&a…...
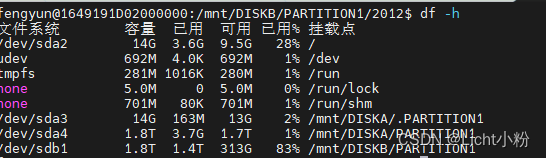
Linux 查看磁盘空间
1 查看当前目录的总大小 :du -sh ps:du(disk usage) 2 查看某个目录的总大小:du -sh 目录名 3 查找出/目录下占用空间最大的前10个文件或者文件夹:sudo du -a / | sort -n -r | head -n 10 4 查看磁盘信息:df -h...
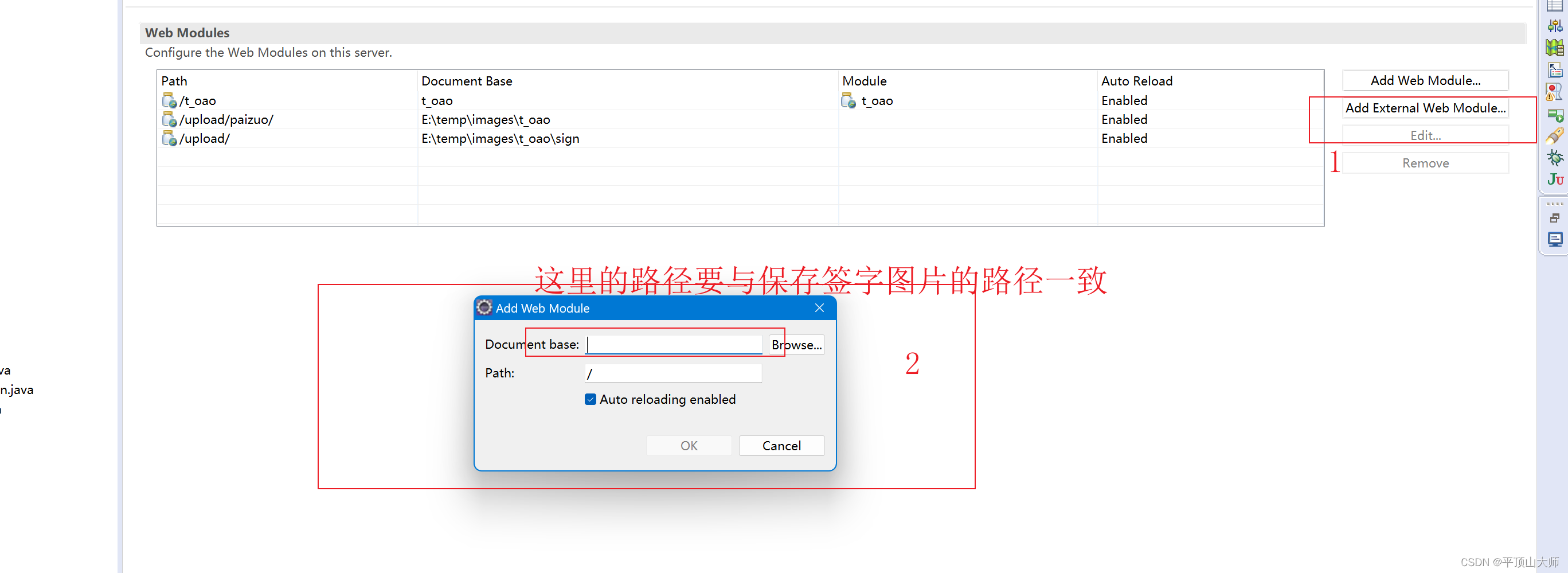
我的会议(我的审批,会议签字附源码)
目录 前言: 3.我的审批: 3.1实现的特色功能: 3.2显示的效果 3.3思路: 3.4寻找相关的案例或者自己使用JavaScript去写一个类似的功能 3.5具体的步骤: 3.5.1添加静态的jsp代码(我的审批数据的显示&…...

Python 装饰器该如何理解?
哈喽大家好,今天带大家了解下在Python中装饰器的使用 定义 首先我们先来了解下装饰器的定义。顾名思义,在Python中,装饰器本质上就是一个函数,它可以接收一个函数作为参数,然后返回一个新的函数。这个新的函数可以在…...
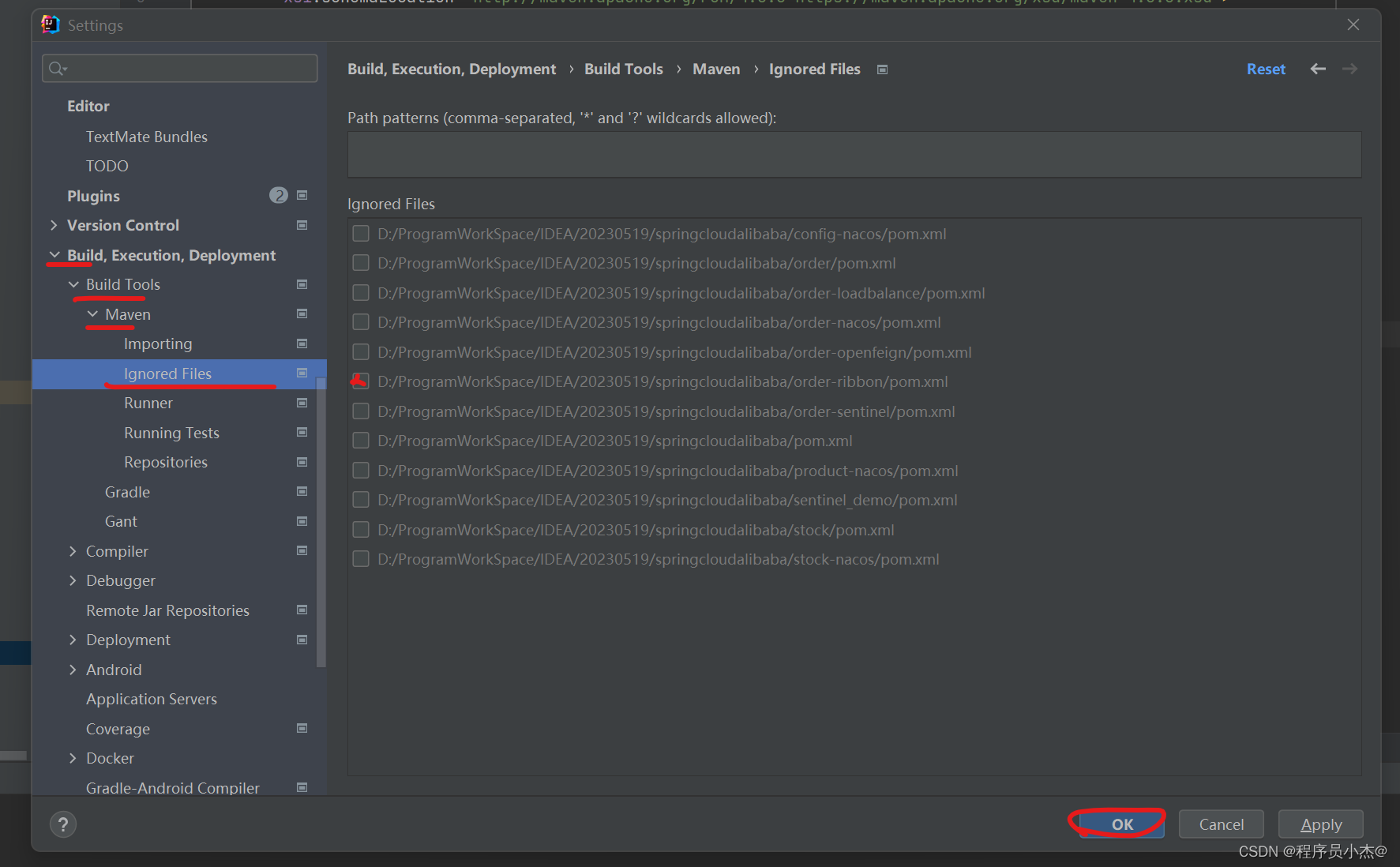
IDEA 模块不加载依旧是灰色 没有变成小蓝色的方块
Settings > Build, Execution, Deployment > Build Tools > Maven > Ignored Files下降对应的模块勾选掉 但通常在Maven的配置中,您会找到一个名为“ignoredFiles”的列表,其中包含被忽略的文件和目录。您可以通过取消选中所需的文件或目录…...
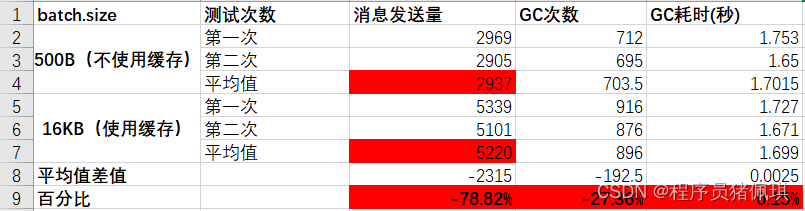
可以写进简历的kafka优化-----吞吐量提升一倍的方法
冲突 在看到项目工程里kafka 生产端配置的batch.size为500,而实际业务数据平均有1K大小的时候;我有点懵了。是的,这里矛盾了;莫非之前的作者认为这个batch.size是发送的条数,而不是kafka生产端内存缓存记录的大小&…...

JavaScript中,for in 和for of的区别
for in 遍历的是数组的索引(即键名),而 for of 遍历的是数组元素值(即键值)。for...in 循环出的是 key,for...of 循环出的是 value 推荐在循环对象属性的时候使用 for...in,在遍历数组的时候的时…...

计算机毕设 深度学习手势识别 - yolo python opencv cnn 机器视觉
文章目录 0 前言1 课题背景2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存 5 模型训练5.1 修…...

vue3 axios接口封装
在Vue 3中,可以通过封装axios来实现接口的统一管理和调用。封装后的接口调用更加简洁,代码可维护性也更好。以下是一个简单的Vue 3中axios接口封装的示例: 1.首先,安装axios和qs(如果需要处理复杂数据)&am…...

誉天程序员-2301-3-day08
4. 书籍管理实现CURD 这个结构比较复杂,是有一套复杂的机制,注意它们之间的关系和控制实现。 新增和修改怎么复用对话框 对话框中的数据,表格中展现的数据,临时记录正在操作的数据统一联动起来 单条删除怎么传递数据&am…...

Python爬虫(1)一次性搞定Selenium(新版)8种find_element元素定位方式
selenium中有8种不错的元素定位方式,每个方式和应用场景都不一样,需要根据自己的使用情况来进行修改 8种find_element元素定位方式 1.id定位2.CSS定位3.XPATH定位4.name定位5.class_name定位6.Link_Text定位7.PARTIAL_LINK_TEXT定位8.TAG_NAME定位总结 …...

前端(十一)——Vue vs. React:两大前端框架的深度对比与分析
😊博主:小猫娃来啦 😊文章核心:Vue vs. React:两大前端框架的深度对比与分析 文章目录 前言概述原理与设计思想算法生态系统与社区支持API与语法性能与优化开发体验与工程化对比总结结语 前言 在当今快速发展的前端领…...
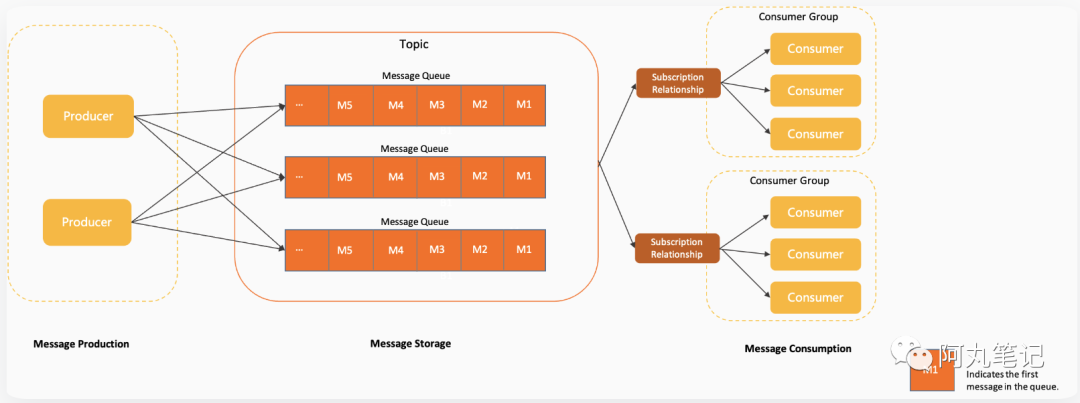
三分钟白话RocketMQ系列—— 核心概念
目录 关键字摘要 Q1:RocketMQ是什么? Q2: 作为消息中间件,RocketMQ和kafka有什么区别? Q3: RocketMQ的基本架构是怎样的? Q4:RocketMQ有哪些核心概念? 总结 RocketMQ是一个开源的分布式消…...

递归竖栏菜单简单思路
自己的项目要写一个竖栏菜单,所以记录一下思路吧,先粗糙的实现一把,有机会再把细节修饰一下 功能上就是无论这个菜单有多少层级,都能显示出来,另外,需要带图标,基于element-plus写成࿰…...

组件化、跨平台…未来前端框架将如何演进?
前端框架在过去几年间取得了显著的进步和演进。前端框架也将继续不断地演化,以满足日益复杂的业务需求和用户体验要求。从全球web发展角度看,框架竞争已经从第一阶段的前端框架之争(比如Vue、React、Angular等),过渡到…...
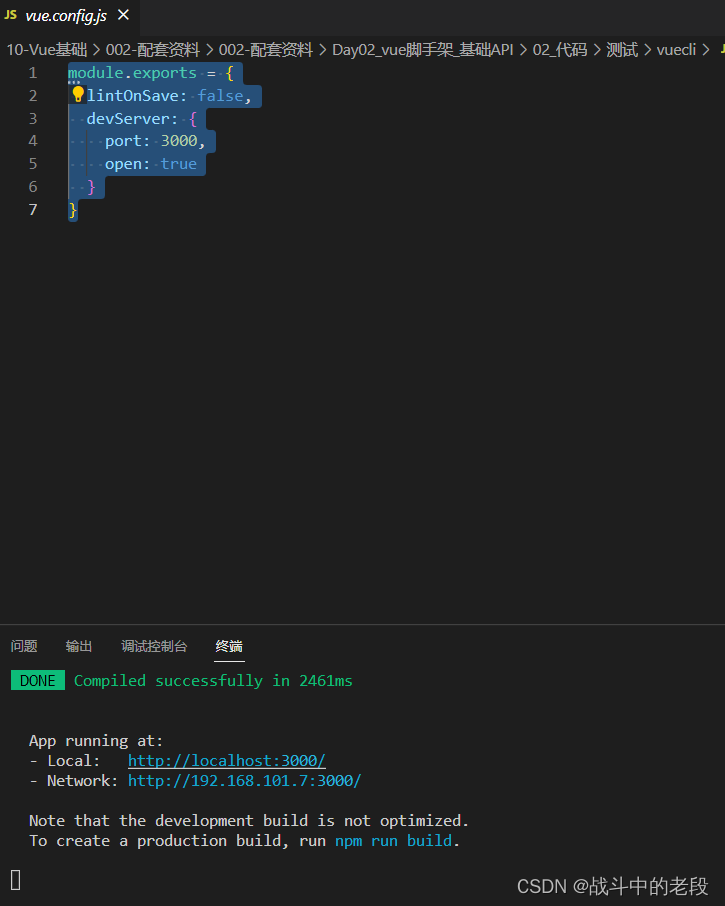
vue 修改端口号
在根目录创建一个vue.config.js文件夹 module.exports {lintOnSave: false,devServer: {port: 3000,open: true} }运行后...

hive的metastore问题汇总
1. metastore内存飙升 1 问题 metastore内存飙升降不下来; spark集群提交的任务无法运行, 只申请到了dirver的资源; 2 原因 当Spark任务无法获取足够资源时,因为任务无法继续进行,不能将元数据从Metastore返回给任务 后,这些元数据暂存在…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
