当前位置： 首页 > news >正文

k8s概念-controller

news 2026/2/10 1:36:25

Controller作用和分类

controller用于控制pod

参考: 工作负载资源 | Kubernetes

控制器主要分为:

  • Deployments 部署无状态应用，控制pod升级,回退

  • ReplicaSet 副本集,控制pod扩容,裁减

  • ReplicationController(相当于ReplicaSet的老版本,现在建议使用Deployments加ReplicaSet替代RC)

  • StatefulSets 部署有状态应用，结合Service、存储等实现对有状态应用部署

  • DaemonSet 守护进程集，运行在所有集群节点(包括master), 比如使用filebeat,node_exporter

  • Jobs 一次性

  • Cronjob 周期性

无状态应用与有状态应用

无状态应用

  • 如nginx

  • 请求本身包含了响应端为响应这一请求所需的全部信息。每一个请求都像首次执行一样，不会依赖之前的数据进行响应。

  • 不需要持久化的数据

  • 无状态应用的多个实例之间互不依赖，可以无序的部署、删除或伸缩

有状态应用

  • 如mysql

  • 前后请求有关联与依赖

  • 需要持久化的数据

  • 有状态应用的多个实例之间有依赖，不能相互替换：无论怎么调度，每个 Pod 都有一个永久不变的 ID。

相关文章：

k8s概念-controller

Controller作用和分类 controller用于控制pod 参考: 工作负载资源 | Kubernetes 控制器主要分为: Deployments 部署无状态应用，控制pod升级,回退 ReplicaSet 副本集,控制pod扩容,裁减 ReplicationController(相当于ReplicaSet的老版本,现在建议使用Deployments…...

编程日记 2023/8/1 19:04:46

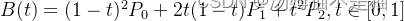
Gis入门，根据起止点和一个控制点计算二阶贝塞尔曲线（共三个控制点组成的线段转曲线）

前言 本章讲解如何在gis地图中使用起止点和一个控制点（总共三个控制点）生成二阶贝塞尔曲线。 三阶贝塞尔曲线请参考下一章《Gis入门，使用起止点和两个控制点生成三阶贝塞尔曲线（共四个控制点）》 贝塞尔曲线（Bezier curve）介绍 贝塞尔曲线（Bezier curve）是一种数学…...

编程日记 2023/8/1 19:03:45

第1集丨Vue 江湖 —— Hello Vue

目录 一、简介1.1 参考网址1.2 下载 二、Hello Vue2.1 创建页面2.2 安装Live Server插件2.4 安装 vue-devtools2.5 预览效果 一、简介 Vue（读音 /vjuː/, 类似于 view） 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是，Vue 被设…...

编程日记 2023/8/1 19:02:44

PCB制版技术

1、在头脑里形成一个原理图----现在就下载AD9盖版，诞生了一个问题，电路板去哪里买，买了怎么焊接电路和芯片，怎样流程化批量制作电子产品 1.1 形成一个PCB板，形成一个结构 1.2 焊接，嫁接，组装等 …...

编程日记 2023/8/1 19:01:43

大数据课程E7——Flume的Interceptor

文章作者邮箱：yugongshiyesina.cn 地址：广东惠州 ▲ 本章节目的 ⚪ 了解Interceptor的概念和配置参数； ⚪ 掌握Interceptor的使用方法； ⚪ 掌握Interceptor的Host Interceptor； ⚪ 掌握Interceptor的…...

编程日记 2023/8/1 19:00:42

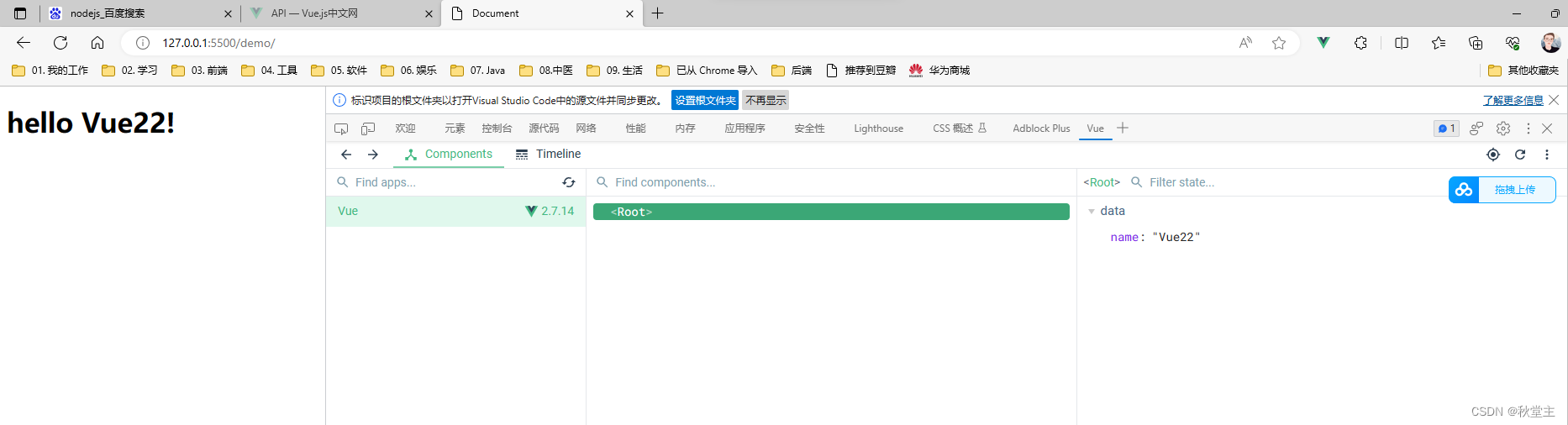
P2P网络NAT穿透原理(打洞方案)

1.关于NAT NAT技术（Network Address Translation，网络地址转换）是一种把内部网络（简称为内网）私有IP地址转换为外部网络（简称为外网）公共IP地址的技术，它使得一定范围内的多台主机只…...

编程日记 2023/8/1 18:59:41

Gof23设计模式之桥接外观模式

1.概述 又名门面模式，是一种通过为多个复杂的子系统提供一个一致的接口，而使这些子系统更加容易被访问的模式。该模式对外有一个统一接口，外部应用程序不用关心内部子系统的具体的细节，这样会大大降低应用程序的复杂度&#xff0…...

编程日记 2023/8/1 18:58:39

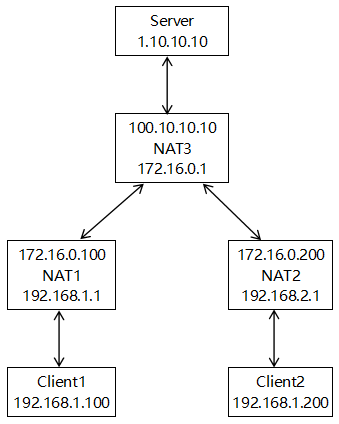
微服务性能分析工具 Pyroscope 初体验

Go 自带接口性能分析工具 pprof，较为常用的有以下 4 种分析： CPU Profiling: CPU 分析，按照一定的频率采集所监听的应用程序 CPU（含寄存器）的使用情况，可确定应用程序在主动消耗 CPU 周期时花费时间的位置…...

编程日记 2023/8/1 18:57:38

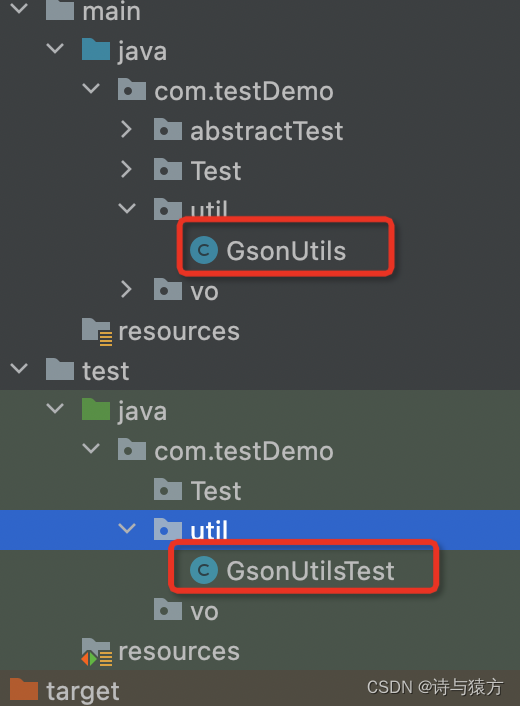
工作记录------单元测试（持续更新）

工作记录------单元测试 之前的工作中从来没有写过单元测试&#xff0c;新入职公司要求写单元测试&#xff0c; 个人觉得&#xff0c;作为程序员单元测试还是必须会写的 于此记录一下首次编写单元测试的过程。 首先引入单元测试相关的依赖 <dependency><groupId>…...

编程日记 2023/8/1 18:56:38

C#再windowForm窗体中绘画扇形并给其填充颜色

C#再windowForm窗体中绘画扇形并给其填充颜色 Graphics graphics this.CreateGraphics();graphics.SmoothingMode SmoothingMode.AntiAlias;int width this.Width;int height this.Height;h this.Height;w this.Width;Rectangle rct new Rectangle(0 - h / 6, 0 - h / 6…...

编程日记 2023/8/1 18:55:37

MBA拓展有感-见好就收，还是挑战到底？MBA拓展有感-见好就收，还是挑战到底？

今天看到新闻提到某位坚持了14年高考的同学滑档&#xff0c;让人心生感叹&#xff1a;无论在日常工作还是生活中&#xff0c;选择都是非常重要的。不由想起前段时间我参加研究生新生拓展时的一些感悟&#xff0c;和大家分享一下。 事情的起因是拓展活动中的一个分队竞技类的活…...

编程日记 2023/8/1 18:54:35

综合布线系统光缆分类及其特点？

综合布线系统光缆是一种用于数据传输和通信的电缆&#xff0c;常用于建筑物内部网络和通信系统的布线。光缆采用光纤作为传输介质&#xff0c;能够以光的形式传输大量数据&#xff0c;具有高带宽、低延迟、抗干扰等特点&#xff0c;适用于高速数据传输和长距离通信需求。 光缆…...

编程日记 2023/8/1 18:53:32

前端构建（打包）工具发展史

大多同学的前端学习路线&#xff1a;三件套框架慢慢延伸到其他&#xff0c;在这个过程中&#xff0c;有一个词出现的频率很高&#xff1a;webpack 。 作为一个很出名的前端构建工具我们在网上随便一搜&#xff0c;就会有各种教程&#xff1a;loader plugin entry吧啦吧啦。 但…...

编程日记 2023/8/1 18:52:31

【数据可视化】（一）数据可视化概述

目录 0.本章节概述 一、数据可视化 1、什么是数据可视化？ 2、数据可视化的好处 3、数据可视化的用途 二、数据探索 1、数据相关工具的使用情景： 2、探索性查询 三、数据挑战 1、什么是数据挑战？...

编程日记 2023/8/1 18:51:30

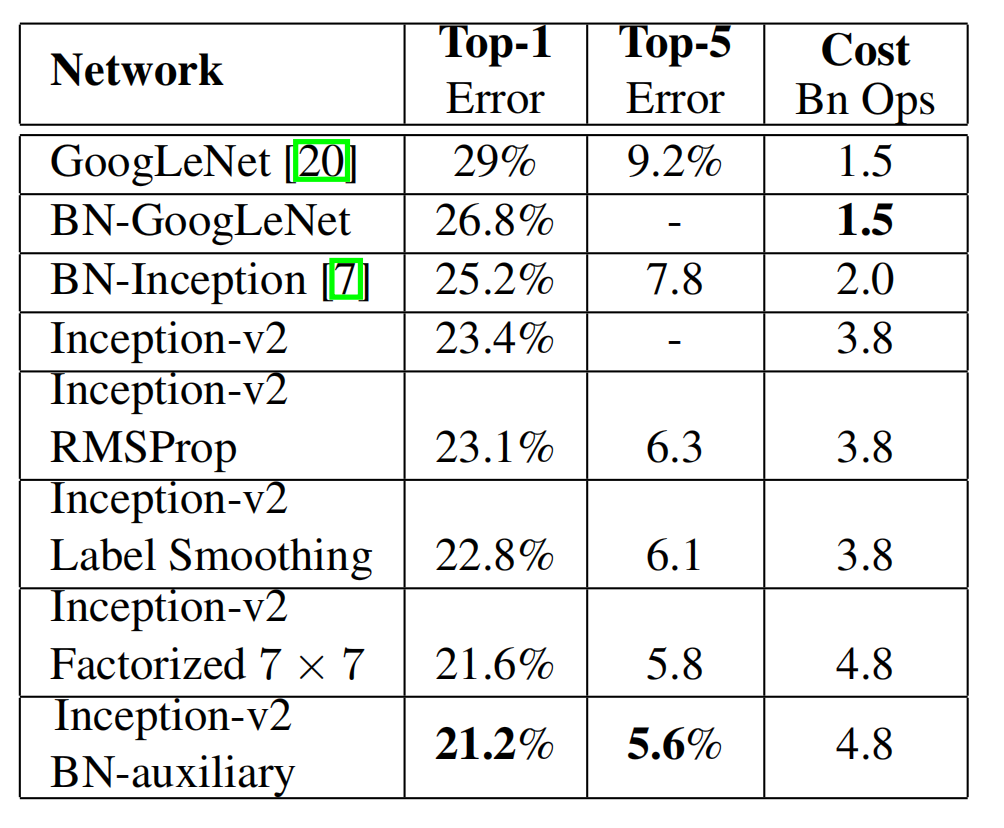
GoogleLeNet Inception V2 V3

文章目录 卷积核分解第一步分解&#xff0c;对称分解第二步分解&#xff0c;非对称分解在Inception中的改造一般模型的参数节省量可能导致的问题 针对两个辅助分类起的改造特征图尺寸缩减Model Regularization via Label Smoothing——LSR问题描述&#xff0c;也就是LSR解决什么…...

编程日记 2023/8/1 18:50:29

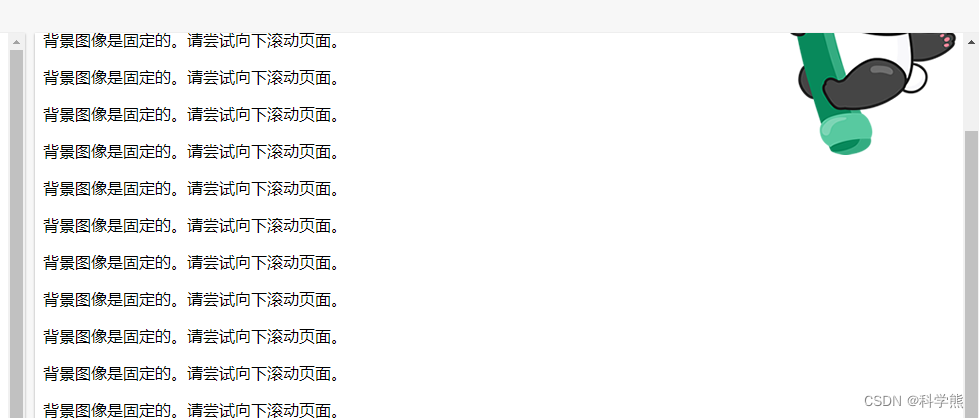
【css】背景图片附着

属性&#xff1a;background-attachment 属性指定背景图像是应该滚动还是固定的&#xff08;不会随页面的其余部分一起滚动&#xff09;。 background-attachment: fixed&#xff1a;为固定&#xff1b; background-attachment: scroll为滚动 代码&#xff1a; <!DOCTYPE h…...

编程日记 2023/8/1 18:49:28

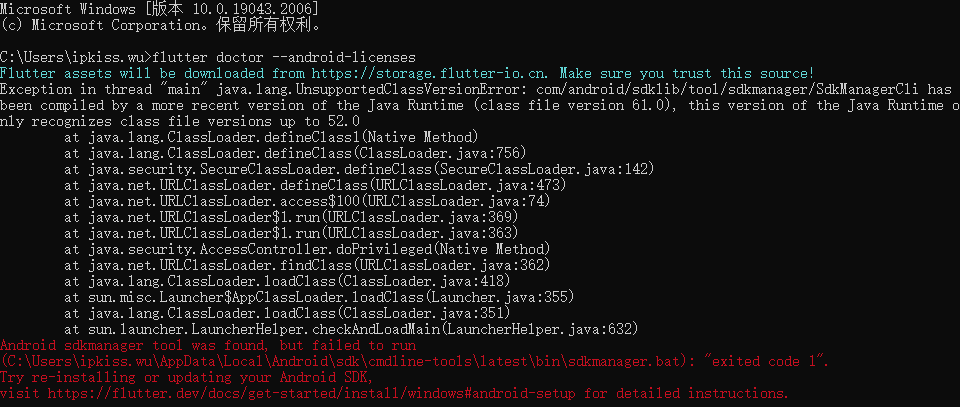
解决运行flutter doctor --android-licenses时报错

问题描述&#xff1a; 配置flutter环境时&#xff0c;会使用flutter doctor命令来检查运行flutter的相关依赖是否配好。能看到还差 Android license status unknown.未解决。 C:\Users\ipkiss.wu>flutter doctor Flutter assets will be downloaded from https://storage.…...

编程日记 2023/8/1 18:48:26

在使用Python爬虫时遇到503 Service Unavailable错误解决办法汇总

在进行Python爬虫的过程中&#xff0c;有时会遇到503 Service Unavailable错误&#xff0c;这意味着所请求的服务不可用&#xff0c;无法获取所需的数据。为了解决这个常见的问题&#xff0c;本文将提供一些解决办法&#xff0c;希望能提供实战价值&#xff0c;让爬虫任务顺利完…...

编程日记 2023/8/1 18:47:25

小研究 - 主动式微服务细粒度弹性缩放算法研究（一）

微服务架构已成为云数据中心的基本服务架构。但目前关于微服务系统弹性缩放的研究大多是基于服务或实例级别的水平缩放&#xff0c;忽略了能够充分利用单台服务器资源的细粒度垂直缩放&#xff0c;从而导致资源浪费。为此&#xff0c;本文设计了主动式微服务细粒度弹性缩放算法…...

编程日记 2023/8/1 18:46:24

【LeetCode】215.数组中的第K个最大元素

题目 给定整数数组 nums 和整数 k&#xff0c;请返回数组中第 k 个最大的元素。 请注意&#xff0c;你需要找的是数组排序后的第 k 个最大的元素&#xff0c;而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入: [3,2,1,5,6,4…...

编程日记 2023/8/1 18:45:22

龙虎榜——20250610

上证指数放量收阴线&#xff0c;个股多数下跌&#xff0c;盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型&#xff0c;指数短线有调整的需求&#xff0c;大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的&#xff1a;御银股份、雄帝科技 驱动…...

编程新知 2026/2/8 15:03:06

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2026/2/8 20:41:49

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关

一、模块概述 ngx_stream_return_module 提供了一个极简的指令&#xff1a; return <value>;在收到客户端连接后&#xff0c;立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量&#xff08;如 $time_iso8601、$remote_addr 等&#xff09;&a…...

编程新知 2025/9/21 0:49:02

多场景 OkHttpClient 管理器 - Android 网络通信解决方案

下面是一个完整的 Android 实现&#xff0c;展示如何创建和管理多个 OkHttpClient 实例&#xff0c;分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

编程新知 2025/12/15 1:34:37

YSYX学习记录（八）

C语言&#xff0c;练习0&#xff1a; 先创建一个文件夹&#xff0c;我用的是物理机&#xff1a; 安装build-essential 练习1&#xff1a; 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件&#xff0c;随机修改或删除一部分&#xff0c;之后…...

编程新知 2026/1/24 14:31:01

在四层代理中还原真实客户端ngx_stream_realip_module

一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡&#xff08;如 HAProxy、AWS NLB、阿里 SLB&#xff09;发起上游连接时&#xff0c;将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后&#xff0c;ngx_stream_realip_module 从中提取原始信息…...

编程新知 2026/1/4 5:02:00

css的定位（position）详解：相对定位 绝对定位 固定定位

在 CSS 中&#xff0c;元素的定位通过 position 属性控制&#xff0c;共有 5 种定位模式&#xff1a;static&#xff08;静态定位&#xff09;、relative&#xff08;相对定位&#xff09;、absolute&#xff08;绝对定位&#xff09;、fixed&#xff08;固定定位&#xff09;和…...

编程新知 2026/2/6 6:35:29

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/11/20 14:26:29

重启Eureka集群中的节点，对已经注册的服务有什么影响

先看答案&#xff0c;如果正确地操作&#xff0c;重启Eureka集群中的节点&#xff0c;对已经注册的服务影响非常小&#xff0c;甚至可以做到无感知。 但如果操作不当&#xff0c;可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

编程新知 2025/9/24 3:38:34

Spring是如何解决Bean的循环依赖：三级缓存机制

1、什么是 Bean 的循环依赖 在 Spring框架中，Bean 的循环依赖是指多个 Bean 之间‌互相持有对方引用‌，形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路，例如： 双向依赖：Bean A 依赖 Bean B，同时 Bean B 也依赖 Bean A（A↔B）。链条循环： Bean A → Bean…...

编程新知 2025/7/25 1:21:53