pgsql 查看某个表建立了那些索引sql
执行以下sql:
SELECTns.nspname as schema_name,tab.relname as table_name,cls.relname as index_name,am.amname as index_type,idx.indisprimary as is_primary,idx.indisunique as is_unique
FROMpg_index idx
INNER JOIN pg_class cls ON cls.oid=idx.indexrelid
INNER JOIN pg_class tab ON tab.oid=idx.indrelid
INNER JOIN pg_am am ON am.oid=cls.relam
INNER JOIN pg_namespace ns on ns.oid=tab.relnamespace
WHERE tab.relname = 'ics_check_report'结果如下:
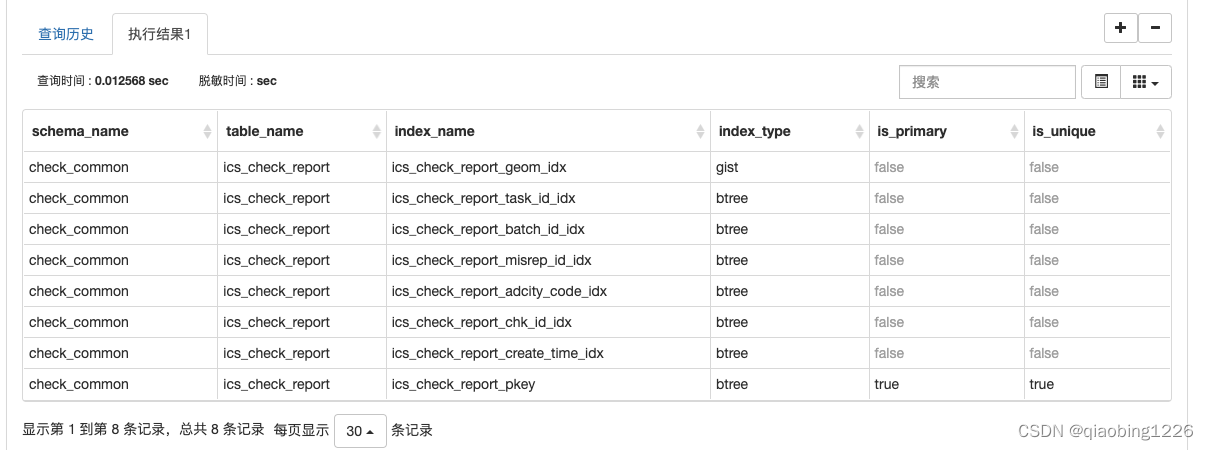
相关文章:

pgsql 查看某个表建立了那些索引sql
执行以下sql: SELECTns.nspname as schema_name,tab.relname as table_name,cls.relname as index_name,am.amname as index_type,idx.indisprimary as is_primary,idx.indisunique as is_unique FROMpg_index idx INNER JOIN pg_class cls ON cls.oididx.indexrel…...

【SCSS】网格布局中的动画
效果 index.html <!DOCTYPE html> <html><head><title> Document </title><link type"text/css" rel"styleSheet" href"index.css" /></head><body><div class"container">&l…...

Docker基础命令(一)
Docker使用1 一、运行终端 打开终端,输入docker images ,如果运行正常,表示docker已经可以在本电脑上使用了 二、docker常用命令 指令说明docker images查看已下载的镜像docker rmi 镜像名称:标签名删除已下载的镜像docker search 镜像从官…...

django4.2 day1Django快速入门
1、创建虚拟环境 打开cmd安装virtualenv pip install virtualenvwrapper-winworkon 查看虚拟环境mkvirtualenv 创建新的虚拟环境删除虚拟环境 rmvirtualenv 进入虚拟环境 workon env 2、创建django虚拟环境并安装django 创建虚拟环境mkvirtualenv django4env进入虚拟环境安…...

linux的exec和system函数介绍及选择
在应用程序中有时候需要调用第三方的应用,这是常见的需求。此时可以使用linux下的exec命令或system命令达到目的。但是这两个该选择哪个呢?有什么区别?下面总结介绍下。 exec和system介绍 在Linux中,exec命令用于在当前进程中执行…...
150行代码写一个Qt井字棋游戏
照例先演示一下: QT井字棋游戏,可以悔棋。 会在鼠标箭头处跟随一个下棋方的小棋子图标。 棋盘和棋子是自己画的,可以自行在对应的代码处更换自己喜欢的图片,不过要注意尺寸兼容。 以棋会友: 井字棋最关键的就是下棋了…...

k8s概念-controller
Controller作用和分类 controller用于控制pod 参考: 工作负载资源 | Kubernetes 控制器主要分为: Deployments 部署无状态应用,控制pod升级,回退 ReplicaSet 副本集,控制pod扩容,裁减 ReplicationController(相当于ReplicaSet的老版本,现在建议使用Deployments…...
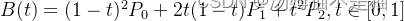
Gis入门,根据起止点和一个控制点计算二阶贝塞尔曲线(共三个控制点组成的线段转曲线)
前言 本章讲解如何在gis地图中使用起止点和一个控制点(总共三个控制点)生成二阶贝塞尔曲线。 三阶贝塞尔曲线请参考下一章《Gis入门,使用起止点和两个控制点生成三阶贝塞尔曲线(共四个控制点)》 贝塞尔曲线(Bezier curve)介绍 贝塞尔曲线(Bezier curve)是一种数学…...
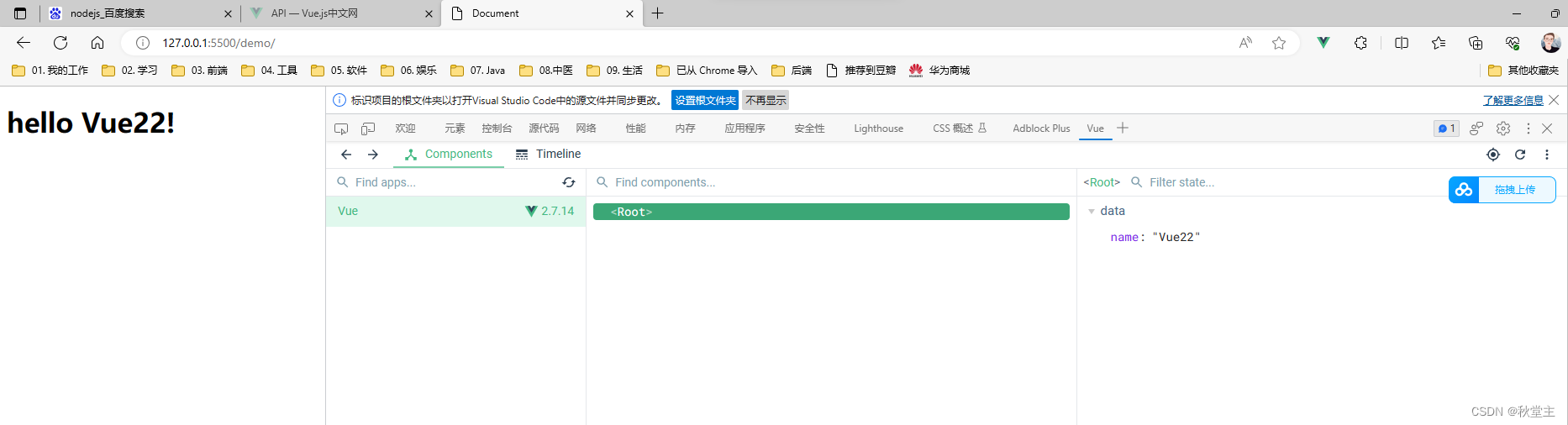
第1集丨Vue 江湖 —— Hello Vue
目录 一、简介1.1 参考网址1.2 下载 二、Hello Vue2.1 创建页面2.2 安装Live Server插件2.4 安装 vue-devtools2.5 预览效果 一、简介 Vue(读音 /vjuː/, 类似于 view) 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是,Vue 被设…...

PCB制版技术
1、在头脑里形成一个原理图----现在就下载AD9盖版,诞生了一个问题,电路板去哪里买,买了怎么焊接电路和芯片,怎样流程化批量制作电子产品 1.1 形成一个PCB板,形成一个结构 1.2 焊接,嫁接,组装等 …...

大数据课程E7——Flume的Interceptor
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Interceptor的概念和配置参数; ⚪ 掌握Interceptor的使用方法; ⚪ 掌握Interceptor的Host Interceptor; ⚪ 掌握Interceptor的…...
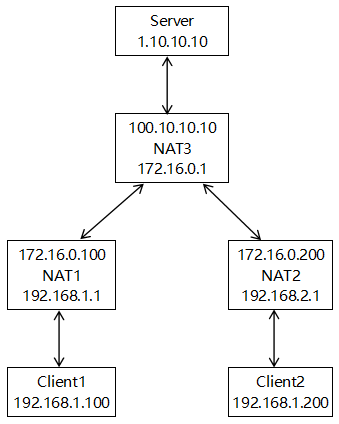
P2P网络NAT穿透原理(打洞方案)
1.关于NAT NAT技术(Network Address Translation,网络地址转换)是一种把内部网络(简称为内网)私有IP地址转换为外部网络(简称为外网)公共IP地址的技术,它使得一定范围内的多台主机只…...

Gof23设计模式之桥接外观模式
1.概述 又名门面模式,是一种通过为多个复杂的子系统提供一个一致的接口,而使这些子系统更加容易被访问的模式。该模式对外有一个统一接口,外部应用程序不用关心内部子系统的具体的细节,这样会大大降低应用程序的复杂度࿰…...
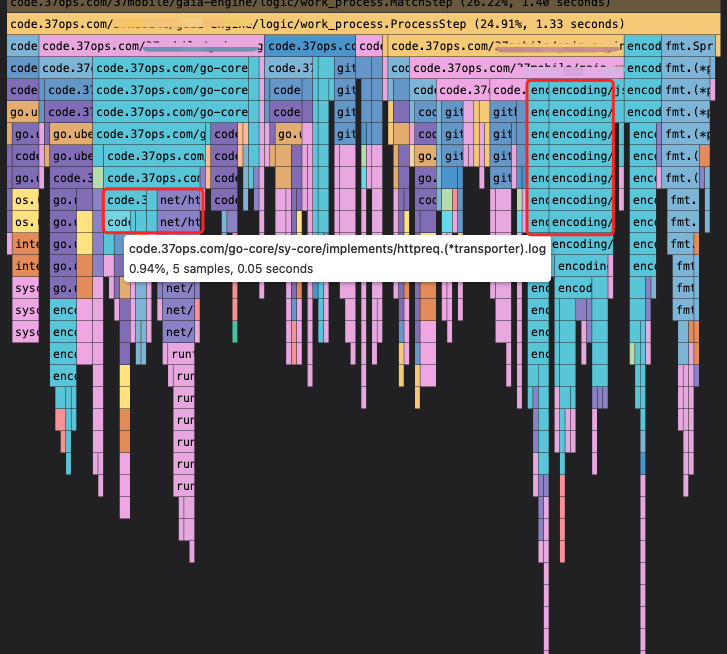
微服务性能分析工具 Pyroscope 初体验
Go 自带接口性能分析工具 pprof,较为常用的有以下 4 种分析: CPU Profiling: CPU 分析,按照一定的频率采集所监听的应用程序 CPU(含寄存器)的使用情况,可确定应用程序在主动消耗 CPU 周期时花费时间的位置…...
工作记录------单元测试(持续更新)
工作记录------单元测试 之前的工作中从来没有写过单元测试,新入职公司要求写单元测试, 个人觉得,作为程序员单元测试还是必须会写的 于此记录一下首次编写单元测试的过程。 首先引入单元测试相关的依赖 <dependency><groupId>…...

C#再windowForm窗体中绘画扇形并给其填充颜色
C#再windowForm窗体中绘画扇形并给其填充颜色 Graphics graphics this.CreateGraphics();graphics.SmoothingMode SmoothingMode.AntiAlias;int width this.Width;int height this.Height;h this.Height;w this.Width;Rectangle rct new Rectangle(0 - h / 6, 0 - h / 6…...

MBA拓展有感-见好就收,还是挑战到底?MBA拓展有感-见好就收,还是挑战到底?
今天看到新闻提到某位坚持了14年高考的同学滑档,让人心生感叹:无论在日常工作还是生活中,选择都是非常重要的。不由想起前段时间我参加研究生新生拓展时的一些感悟,和大家分享一下。 事情的起因是拓展活动中的一个分队竞技类的活…...

综合布线系统光缆分类及其特点?
综合布线系统光缆是一种用于数据传输和通信的电缆,常用于建筑物内部网络和通信系统的布线。光缆采用光纤作为传输介质,能够以光的形式传输大量数据,具有高带宽、低延迟、抗干扰等特点,适用于高速数据传输和长距离通信需求。 光缆…...

前端构建(打包)工具发展史
大多同学的前端学习路线:三件套框架慢慢延伸到其他,在这个过程中,有一个词出现的频率很高:webpack 。 作为一个很出名的前端构建工具我们在网上随便一搜,就会有各种教程:loader plugin entry吧啦吧啦。 但…...
数据可视化概述)
【数据可视化】(一)数据可视化概述
目录 0.本章节概述 一、数据可视化 1、什么是数据可视化? 2、数据可视化的好处 3、数据可视化的用途 二、数据探索 1、数据相关工具的使用情景: 2、探索性查询 三、数据挑战 1、什么是数据挑战?...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
