当前位置： 首页 > news >正文

EMC VNX1系列存储电池状态说明

news 2026/2/9 16:15:25

SPS电池正常的状态为“Present”。
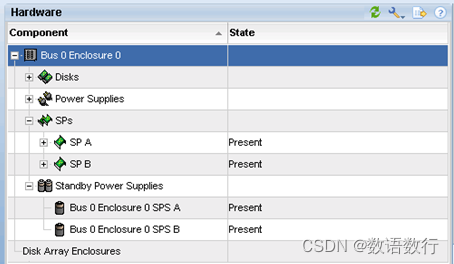
在这里插入图片描述

SPS电池故障时的状态为“Faulted”。
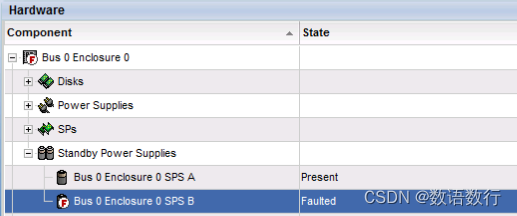
在这里插入图片描述

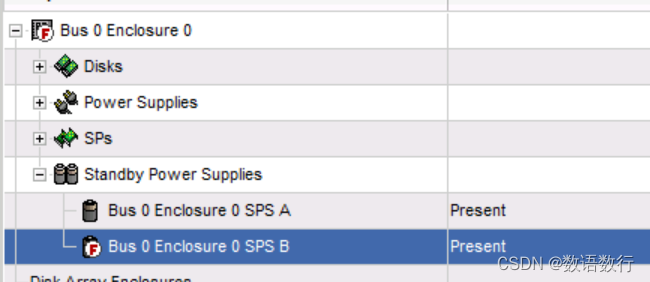
更换SPS后，SPS开始充电，此时状态显示为“Not Ready”状态。
在这里插入图片描述


充电完成后显示为Present状态。如果充电完成后状态前面有“F”标记，则需要重启对应的控制器以更新SPS的状态。
在这里插入图片描述

相关文章：

EMC VNX1系列存储电池状态说明

SPS电池正常的状态为“Present”。 SPS电池故障时的状态为“Faulted”。 更换SPS后，SPS开始充电，此时状态显示为“Not Ready”状态。 充电完成后显示为Present状态。如果充电完成后状态前面有“F”标记，则需要重启对应的控制器以更新SPS…...

编程日记 2023/8/1 19:32:48

pyspark 判断 Hive 表是否存在

Catalog.tableExists(tableName: str, dbName: Optional[str] None) → booltableName:表名 dbName：库名(可选) return：bool 值 spark SparkSession \.builder \.appName(tableExists) \.config(spark.num.executors, 6) \.config(spark.executor.memo…...

编程日记 2023/8/1 19:31:47

选择排序算法

选择排序 算法说明与代码实现&#xff1a; 以下是使用Go语言实现的选择排序算法示例代码&#xff1a; package mainimport "fmt"func selectionSort(arr []int) {n : len(arr)for i : 0; i < n-1; i {minIndex : ifor j : i 1; j < n; j {if arr[j] < a…...

编程日记 2023/8/1 19:30:46

快速了解MyBatis---映射关系多对一

文章目录 映射关系多对一映射关系-官方文档映射关系多对1-基本介绍基本介绍注意细节 映射关系多对1-映射方式映射方式配置Mapper.xml 方式-应用实例注解实现多对1 映射-应用实例 映射关系多对一 映射关系-官方文档 文档地址: https://mybatis.org/mybatis-3/zh/sqlmap-xml.ht…...

编程日记 2023/8/1 19:29:45

python学到什么程度算入门,python从入门到精通好吗

本篇文章给大家谈谈python学到什么程度算入门&#xff0c;以及python从入门到精通好吗&#xff0c;希望对各位有所帮助&#xff0c;不要忘了收藏本站喔。 学习 Python 之 进阶学习 一切皆对象 1. 变量和函数皆对象2. 模块和类皆对象3. 对象的基本操作 (1). 可以赋值给变量(2). …...

编程日记 2023/8/1 19:28:40

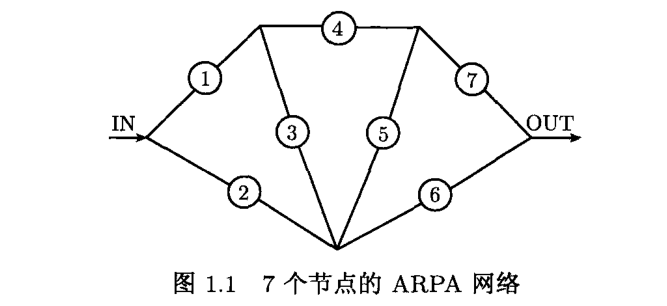
整数规划——第一章 引言

整数规划——第一章 引言 整数规划是带整数变量的最优化问题&#xff0c;即最大化或最小化一个全部或部分变量为整数的多元函数受约束于一组等式和不等式条件的最优化问题。许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模。 考虑一个电视机工厂的生产…...

编程日记 2023/8/1 19:27:39

C语言结构体讲解

目录 结构体的声明 结构的基础知识 结构的声明 为什么要出现结构体&#xff1f; 结构成员的类型 结构体变量的定义和初始化 定义&#xff1a;&#xff08;全局变量//局部变量&#xff09; 初始化&#xff1a; 结构体成员的访问 结构体传参 结构体的声明 结构的基础知识…...

编程日记 2023/8/1 19:26:38

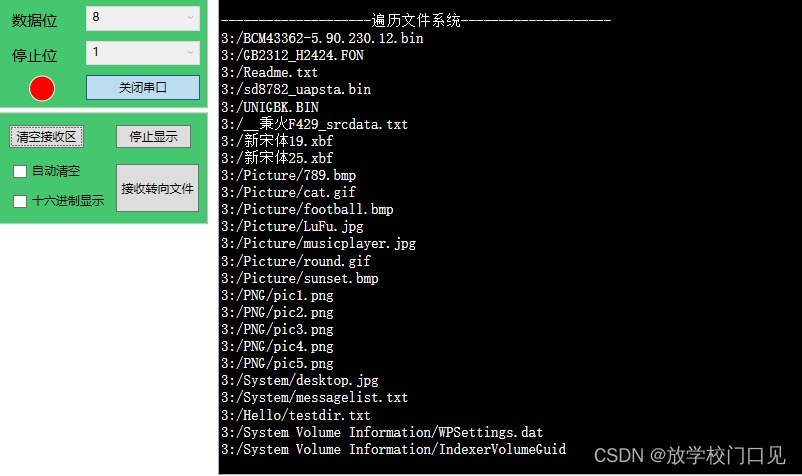
021 - STM32学习笔记 - Fatfs文件系统（三） - 细化与总结

021 - STM32学习笔记 - Fatfs文件系统&#xff08;三&#xff09; - 细化与总结 上节内容中&#xff0c;初步实现了FatFs文件系统的移植&#xff0c;并且实现了设备的挂载、文件打开/关闭与读写功能&#xff0c;这里对上节遗留的一些问题进行总结&#xff0c;并且继续完善文件…...

编程日记 2023/8/1 19:25:37

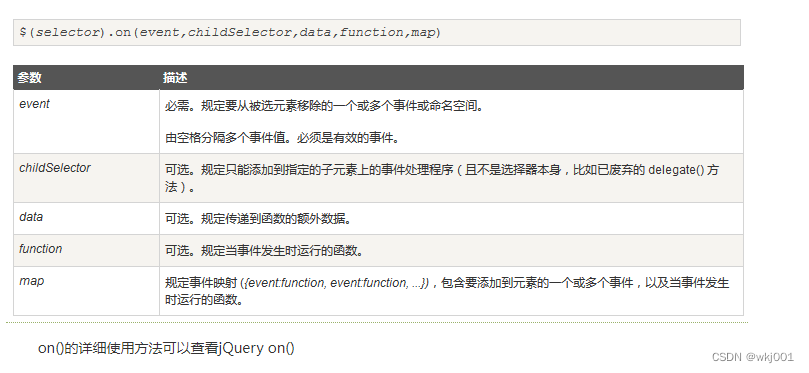
jQuery如何获取动态添加的元素

jQuery如何获取动态添加的元素 使用 on()方法 本质上使用了事件委派&#xff0c;将事件委派在父元素身上 自 jQuery 版本 1.7 起&#xff0c;on() 方法是 bind()、live() 和 delegate() 方法的新的替代品&#xff0c;但是由于on()方法必须有事件&#xff0c;没有事件时可选择de…...

编程日记 2023/8/1 19:24:36

Keepalived 在CentOS 7安装并配置监听MySQL双主

keepalived安装 MySQL双主配置请看这里&#xff1a;https://tongyao.blog.csdn.net/article/details/132016200?spm1001.2014.3001.5502 128、129两台服务器安装步骤相同&#xff0c;配置文件不同&#xff0c;下面有介绍。 1.安装相关依赖包&#xff0c;并下载keepalived安…...

编程日记 2023/8/1 19:23:34

深度学习，神经网络介绍

目录 1.神经网络的整体构架 2.神经网络架构细节 3.正则化与激活函数 4.神经网络过拟合解决方法 1.神经网络的整体构架 ConvNetJS demo: Classify toy 2D data 我们可以看看这个神经网络的网站&#xff0c;可以用来学习。 神经网络的整体构架如下1&#xff1a; 感知器&…...

编程日记 2023/8/1 19:22:32

中国AI大模型峰会“封神之作”！开发者不容错过这场夏季盛会

年度最强大模型顶会来袭&#xff01;喊话中国数百万AI开发者&#xff0c;速来&#xff01; 硬核来袭&#xff01;中国AI大模型峰会“封神之作”&#xff0c;开发者们不容错过! 前瞻大模型发展趋势&#xff0c;紧跟这场大会&#xff01; 中国科技超级碗&#xff0c;大模型最新前…...

编程日记 2023/8/1 19:21:31

Android Studio多渠道打包

使用环境&#xff1a; Android studio 多渠道打包 使用方法&#xff1a; 1 APP下build.gradle文件 flavorDimensions "default"productFlavors {huawei {dimension "default"manifestPlaceholders [ channel:"huawei" ]}xiaomi {dimension &…...

编程日记 2023/8/1 19:20:30

RK3566 Android11默认客户Launcher修改

前言 客户需要默认自己的Launcher为home，同时保留系统的Launcher3. 解决办法：在启动home应用之前设置一下默认Launcher。查找home app启动相关资料，找到了frameworks/base/services/core/java/com/android/server/wm/RootWindowContainer.java的startHomeOnTaskDisplayA…...

编程日记 2023/8/1 19:19:27

ORB算法在opencv中实现方法

在OPenCV中实现ORB算法&#xff0c;使用的是&#xff1a; 1.实例化ORB orb cv.xfeatures2d.orb_create(nfeatures)参数&#xff1a; nfeatures: 特征点的最大数量 2.利用orb.detectAndCompute()检测关键点并计算 kp,des orb.detectAndCompute(gray,None)参数&#xff1a…...

编程日记 2023/8/1 19:18:26

vue项目回显文本无法识别换行符

解决方法 1&#xff1a;使用<br/>替换文本中的\n&#xff0c;使用v-html渲染 <template> <div v-html"str"></div> </template> <script> let str 以下内容自动换行\n换行了 // 使用replace截取提换 this.str str.replace(/…...

编程日记 2023/8/1 19:17:25

Minio 部署

minio 官网&#xff1a;https://www.minio.org.cn/ 部署文档&#xff1a;https://www.minio.org.cn/docs/minio/container/operations/install-deploy-manage/deploy-minio-single-node-single-drive.html# 选择自己的部署环境&#xff1a; 我用的docker: docker pull qua…...

编程日记 2023/8/1 19:16:24

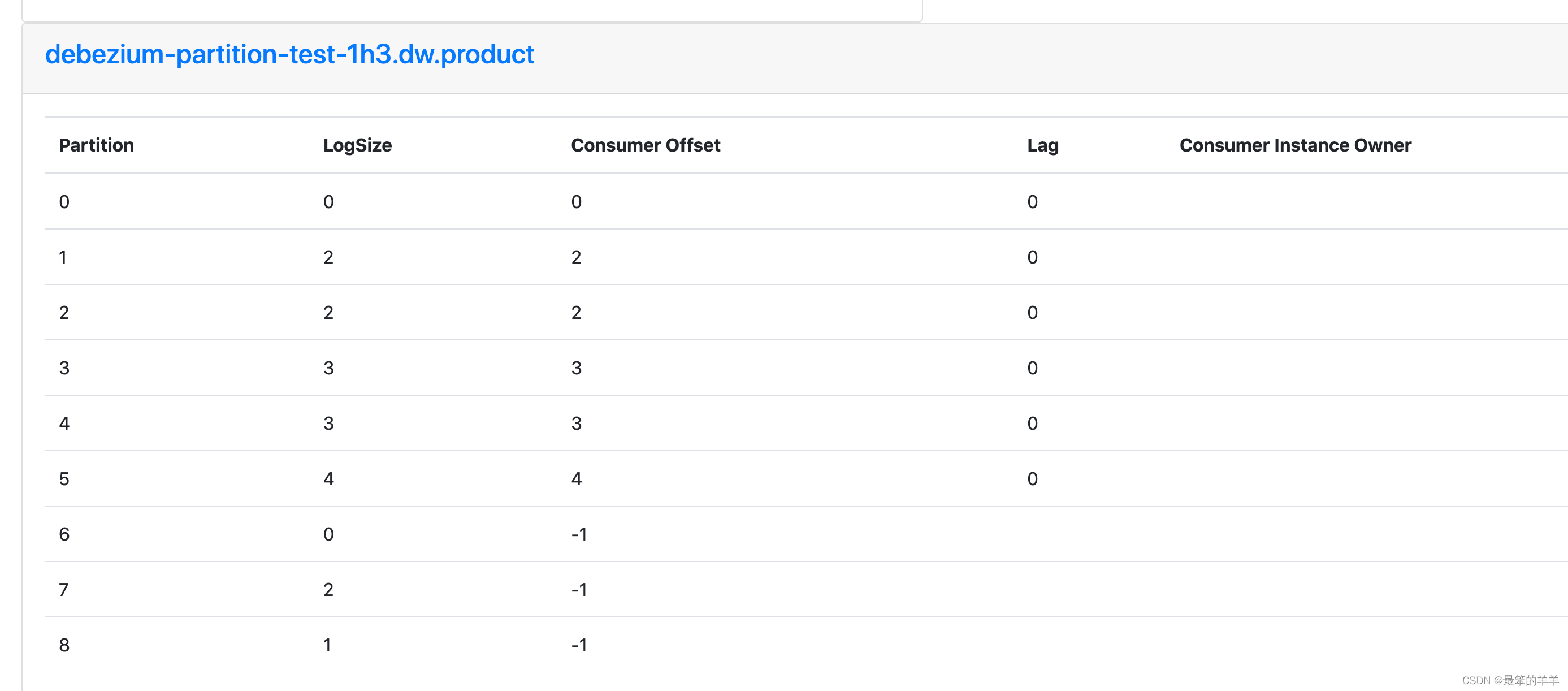
Kafka系列之：记录一次Kafka Topic分区扩容，但是下游flink消费者没有自动消费新的分区的解决方法

Kafka系列之：记录一次Kafka Topic分区扩容，但是下游flink消费者没有自动消费新的分区的解决方法 一、背景二、解决方法三、实现自动发现新的分区一、背景 生产环境Kafka集群压力大，Topic读写压力大，消费的lag比较大，因此通过扩容Topic的分区，增大Topic的读写性能理论上下…...

编程日记 2023/8/1 19:15:23

Ansible部署MariaDB galera集群(多主)

文章目录 Ansible部署MariaDB galera集群(多主)介绍节点规划基础环境准备编写剧本文件执行剧本文件查看集群状态测试 Ansible部署MariaDB galera集群(多主) 介绍 MariaDB Galera集群是一套基于同步复制的、多主的MySQL集群解决方案&#xff0c;使用节点没有单点故障&#xff…...

编程日记 2023/8/1 19:14:20

立体库-库龄

split 用法第一种&#xff1a; 1.对单个字符进行分割&#xff08;注意这里是字符&#xff0c;不是字符串&#xff0c;故只能用单引号‘’&#xff09; string sabcdeabcdeabcde; string[] sArrays.Split(c) ; foreach(string i in sArray) Console.WriteLine(i.ToString());…...

编程日记 2023/8/1 19:13:19

Golang 面试经典题：map 的 key 可以是什么类型？哪些不可以？

Golang 面试经典题&#xff1a;map 的 key 可以是什么类型&#xff1f;哪些不可以&#xff1f; 在 Golang 的面试中&#xff0c;map 类型的使用是一个常见的考点&#xff0c;其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

编程新知 2025/12/20 7:42:02

华为OD机试-食堂供餐-二分法

import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

编程新知 2026/1/28 11:11:03

C# SqlSugar：依赖注入与仓储模式实践

C# SqlSugar&#xff1a;依赖注入与仓储模式实践 在 C# 的应用开发中&#xff0c;数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护&#xff0c;许多开发者会选择成熟的 ORM&#xff08;对象关系映射&#xff09;框架&#xff0c;SqlSugar 就是其中备受…...

编程新知 2025/11/25 6:49:02

【JavaSE】绘图与事件入门学习笔记

-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角&#xff0c;以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向&#xff0c;距离坐标原点x个像素;第二个是y坐标&#xff0c;表示当前位置为垂直方向&#xff0c;距离坐标原点y个像素。 坐标体系-像素 …...

编程新知 2025/12/19 20:46:15

Hive 存储格式深度解析：从 TextFile 到 ORC，如何选对数据存储方案？

在大数据处理领域&#xff0c;Hive 作为 Hadoop 生态中重要的数据仓库工具&#xff0c;其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式&#xff0c;很多开发者常常陷入选择困境。本文将从底…...

编程新知 2025/12/6 10:54:35

uniapp手机号一键登录保姆级教程（包含前端和后端）

目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号&#xff08;第三种&#xff09;后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

编程新知 2026/1/27 2:03:36

从面试角度回答Android中ContentProvider启动原理

Android中ContentProvider原理的面试角度解析&#xff0c;分为​​已启动​​和​​未启动​​两种场景&#xff1a; 一、ContentProvider已启动的情况 1. ​​核心流程​​ ​​触发条件​​&#xff1a;当其他组件&#xff08;如Activity、Service&#xff09;通过ContentR…...

编程新知 2025/10/2 19:46:59

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]

报错信息&#xff1a;libc.so.6: cannot open shared object file: No such file or directory&#xff1a; #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

编程新知 2026/2/5 14:35:21

Canal环境搭建并实现和ES数据同步

作者&#xff1a;田超凡 日期&#xff1a;2025年6月7日 Canal安装&#xff0c;启动端口11111、8082&#xff1a; 安装canal-deployer服务端&#xff1a; https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

编程新知 2026/2/1 18:11:41

从零手写Java版本的LSM Tree （一）：LSM Tree 概述

&#x1f525; 推荐一个高质量的Java LSM Tree开源项目&#xff01; https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree&#xff0c;专为高并发写入场景设计。 核心亮点&#xff1a; ⚡ 极致性能&#xff1a;写入速度超…...

编程新知 2026/2/8 2:26:12