整数规划——第一章 引言
整数规划——第一章 引言
整数规划是带整数变量的最优化问题,即最大化或最小化一个全部或部分变量为整数的多元函数受约束于一组等式和不等式条件的最优化问题。许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模。
考虑一个电视机工厂的生产计划问题,如果线性规划模型给出的最优生产计划是每天生产102。4台,则可以选择每天102或103台的生产计划。另一方面,若考虑的问题是仓库的选址问题,设线性规划给出的最优解是在甲地点建或买0。6个仓库,在乙地点建或买0。4个仓库,因仓库的个数必须是整数,这时线性规划的解不能提供任何有用的决策方案。实际上,除了可以描述决策变量的离散性外,整数变量可以帮助我们刻画最优化建模中的许多约束条件,如逻辑关系、固定费用、可选变量的上界、顺序和排序关系、分片线性函数等。
整数规划的历史可以追溯到20世纪50年代,运筹学创始人和线性规划单纯形算法发明者Dantzig首先发现可以用0-1变量来刻画最优化模型中的固定费用、变量上界、非凸分片线性函数等。他和Fulkerson及Johnson对旅行售货员问题(TSP)的研究成为后来的分枝割方法和现代混合整数规划算法的开端。1958年,Gomory发现了第一个一般线性整数规划的收敛算法——割平面方法。随着整数规划理论和算法的发展,整数规划已成为应用最广泛的最优化方法之一,特别是近年来整数规划算法技术和软件系统(如CPLEX)的发展和推广,整数规划在生产企业、服务、运营管理、交通、通信等领域得到了极大的应用和发展。
1.1 分类与建模
1.1.1 线性混合整数规划
线性混合整数规划(Mixed integer program/programming,MIP)的一般形式为:
( MIP ) min c T x + h T y , s . t . A x + G y ≤ b , x ∈ Z + n , y ∈ R + p , \begin{aligned} (\text{MIP})\quad\quad& \min \ c^T x+h^Ty,\\\ & s.t.\quad Ax+Gy\le b,\ x\in \Z^n_+,y\in \R^p_+, \end{aligned} (MIP) min cTx+hTy,s.t.Ax+Gy≤b, x∈Z+n,y∈R+p,
其中 Z + n \Z^n_+ Z+n 是 n n n 维非负整数向量集合, R + p \R^p_+ R+p 是 p p p 维非负实数向量集合。
如果问题(MIP)中没有连续决策变量,则(MIP)就是一个(纯)线性整数规划:
( IP ) min c T x , s . t . A x ≤ b , x ∈ Z + n , \begin{aligned} (\text{IP})\quad\quad& \min \ c^T x,\\\ & s.t.\quad Ax\le b,\ x\in \Z^n_+, \end{aligned} (IP) min cTx,s.t.Ax≤b, x∈Z+n,
背包问题 设有一个背包,其承重为 b b b 。考虑n件物品,其中第 j j j 件的重量为 α j α_j αj ,价值为 c j c_j cj。问如何选取物品装入背包,使背包内物品的总价值最大?
设
x j = { 1 , 若选取第 j 件物品, 0 , 若不选取 . x_j=\begin{cases} 1,&若选取第j件物品,\\ 0,&若不选取. \end{cases} xj={1,0,若选取第j件物品,若不选取.
则背包问题可以表示为下列线性0-1规划:
max ∑ j = 1 n c j x j , s . t . ∑ j = 1 n a j x j ≤ b , x ∈ { 0 , 1 } n . \begin{aligned}&\max \sum_{j=1}^n c_jx_j,\\ &s.t.\ \sum_{j=1}^n a_jx_j\le b,\\ &\quad\quad x\in \{0,1\}^n. \end{aligned} maxj=1∑ncjxj,s.t. j=1∑najxj≤b,x∈{0,1}n.
指派问题 设有 m m m 台机器, n n n 个工件,第 i i i 台机器的可用工时数为 b i b_i bi ,第 i i i 台机器完成第 j j j 件工件需要的工时数为 a i j a_{ij} aij ,费用为 c i j c_{ij} cij 。问如何最优指派机器生产。
设
x i j = { 1 , 若第 i 个机器加工第 j 件工件, 0 , 其他 . x_{ij}=\begin{cases} 1,&若第\ i\ 个机器加工第\ j\ 件工件,\\ 0,&其他. \end{cases} xij={1,0,若第 i 个机器加工第 j 件工件,其他.
则指派问题可以表示为如下0-1规划问题:
min ∑ i = 1 n ∑ j = 1 n c i j x i j , s . t . ∑ j = 1 n a i j x i j ≤ b i , i = 1 , . . . , m , ∑ i = 1 m x i j = 1 , j = 1 , . . . , n , x ∈ { 0 , 1 } n . \begin{aligned}&\min \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij},\\ &s.t.\ \sum_{j=1}^n a_{ij}x_{ij}\le b_i,\ i = 1,...,m,\\ &\quad\quad\sum_{i = 1}^m x_{ij} =1,j=1,...,n, \\ &\quad\quad x\in \{0,1\}^n. \end{aligned} mini=1∑nj=1∑ncijxij,s.t. j=1∑naijxij≤bi, i=1,...,m,i=1∑mxij=1,j=1,...,n,x∈{0,1}n.
集合覆盖问题 设某地区划分为若干个区域,需要建立若干个应急服务中心(如消防站、急救中心等),每个中心的建立都需要一笔建站费用,设候选中心的位置已知,每个中心可以服务的区域预先知道,问如何选取中心使该应急服务能覆盖整个地区且使建站费用最小。
记 M = { 1 , ⋅ ⋅ ⋅ , m } M=\{1,···,m\} M={1,⋅⋅⋅,m} 为该地区中的区域, N = { 1 , ⋅ ⋅ ⋅ , n } N=\{1,···,n\} N={1,⋅⋅⋅,n} 是可选的中心,设 S ≤ M S≤M S≤M 为中心 j ∈ N j∈N j∈N 可以服务的区域集合, c j c_j cj 是中心 j j j 的建站费用,定义0-1关联矩阵 A = ( a i j ) A=(a_{ij}) A=(aij) ,其中如果 i ∈ S j i∈S_j i∈Sj, a i j = 1 a_{ij}=1 aij=1 ,否则 a i j = 0 a_{ij}=0 aij=0 。
设
x j = { 1 , 若选取中心 j , 0 , 其他 . x_j=\begin{cases} 1,&若选取中心j,\\ 0,&其他. \end{cases} xj={1,0,若选取中心j,其他.
则问题可以表述为:
min ∑ j = 1 n c j x j , s . t . ∑ j = 1 n a i j x j ≥ 1 , i = 1 , . . . , m , x ∈ { 0 , 1 } n . \begin{aligned}&\min \sum_{j=1}^n c_jx_j,\\ &s.t.\ \sum_{j=1}^n a_{ij}x_j\ge 1,i=1,...,m,\\ &\quad\quad x\in \{0,1\}^n. \end{aligned} minj=1∑ncjxj,s.t. j=1∑naijxj≥1,i=1,...,m,x∈{0,1}n.
旅行售货员问题(TSP) 设有一个旅行售货员需要去n个城市推销他的产品,他必须而且只能访问每个城市一次,并最后返回出发城市.设每个城市直接到达另一个城市的距离已知(如不能直接到达,则可设其距离为+∞),他应该如何选择旅行路线使得总的旅行距离最短?
设城市 i i i 到城市 j j j 的距离为 c i j c_{ij} cij,设
x i j = { 1 , 若他的旅游路线包括了直接从城市 i 到城市 j 的行程, 0 , 其他 . x_{ij}=\begin{cases} 1,&若他的旅游路线包括了直接从城市 i 到城市 j的行程,\\ 0,&其他. \end{cases} xij={1,0,若他的旅游路线包括了直接从城市i到城市j的行程,其他.
约束条件:
离开城市 i i i 一次:
∑ j ≠ i x i j = 1 , i = 1 , . . . , n \sum_{j\not= i}x_{ij}=1,\ i=1,...,n j=i∑xij=1, i=1,...,n
到达城市 j j j 一次:
∑ i ≠ j x i j = 1 , j = 1 , . . . , n \sum_{i\not= j}x_{ij}=1,\ j=1,...,n i=j∑xij=1, j=1,...,n
上面的约束条件使得每个城市正好经过一次,但仍可能包括含圈但不联通的路
线,我们需要用下面的约束条件来去除这种情况发生:∑ i ∈ S ∑ j ∉ S x i j ≥ 1 , ∀ S ⊂ N = { 1 , . . . , n } , S ≠ ∅ \sum_{i\in S}\sum_{j\not\in S}x_{ij}\ge 1,\quad \forall S\sub N=\{1,...,n\},S\not =\emptyset i∈S∑j∈S∑xij≥1,∀S⊂N={1,...,n},S=∅
或者
∑ i ∈ S ∑ j ∈ S x i j ≤ ∣ S ∣ − 1 , ∀ S ⊂ N , 2 ≤ ∣ S ∣ ≤ n − 1 \sum_{i\in S}\sum_{j\in S} x_{ij}\le |S|-1,\quad \forall S\sub N,\quad 2\le|S|\le n-1 i∈S∑j∈S∑xij≤∣S∣−1,∀S⊂N,2≤∣S∣≤n−1
从而旅行售货员问题可以表示为:
min ∑ i = 1 n ∑ j = 1 n c i j x i j , s . t . ∑ j ≠ i x i j = 1 , i = 1 , . . . , n , ∑ i ≠ j m x i j = 1 , j = 1 , . . . , n , ∑ i ∈ S ∑ j ∈ S x i j ≤ ∣ S ∣ − 1 , ∀ S ⊂ N , 2 ≤ ∣ S ∣ ≤ n − 1 , x ∈ { 0 , 1 } n . \begin{aligned}&\min \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij},\\ &s.t.\ \sum_{j\not=i} x_{ij}=1,\ i = 1,...,n,\\ &\quad\quad\sum_{i \not= j}^m x_{ij} =1,j=1,...,n, \\ &\quad\quad\sum_{i\in S}\sum_{j\in S} x_{ij}\le |S|-1,\quad \forall S\sub N,\quad 2\le|S|\le n-1,\\ &\quad\quad x\in \{0,1\}^n. \end{aligned} mini=1∑nj=1∑ncijxij,s.t. j=i∑xij=1, i=1,...,n,i=j∑mxij=1,j=1,...,n,i∈S∑j∈S∑xij≤∣S∣−1,∀S⊂N,2≤∣S∣≤n−1,x∈{0,1}n.
1.1.2 非线性整数规划
一般非线性混合整数规划(Mixed-Integer Nonlinear Programming)问题可表示为;
( MINLP ) min f ( x , y ) , s . t . g i ( x , y ) ≤ b i , i = 1 , . . . , m , x ∈ X , y ∈ Y \begin{aligned} (\text{MINLP})\quad\quad& \min f(x,y),\\\ & s.t.\quad g_i(x,y)\le b_i,\quad i =1,...,m,\\ &\quad\quad\ \ \ x \in X,\quad y\in Y \end{aligned} (MINLP) minf(x,y),s.t.gi(x,y)≤bi,i=1,...,m, x∈X,y∈Y
此处的 f , g i , i = 1 , . . . , m f,g_i,i=1,...,m f,gi,i=1,...,m 是 R n + q \R^{n+q} Rn+q 上的实值函数, X X X 是 Z n \Z^n Zn 的子集, Y Y Y 是 R q \R^q Rq 的子集。
当(MINLP)中没有连续变量 y y y 时,(MINLP)即是一个(纯)非线性整数规划:
( NLIP ) min f ( x , y ) , s . t . g i ( x , y ) ≤ b i , i = 1 , . . . , m , x ∈ X , y ∈ Y \begin{aligned} (\text{NLIP})\quad\quad& \min f(x,y),\\\ & s.t.\quad g_i(x,y)\le b_i,\quad i =1,...,m,\\ &\quad\quad\ \ \ x \in X,\quad y\in Y \end{aligned} (NLIP) minf(x,y),s.t.gi(x,y)≤bi,i=1,...,m, x∈X,y∈Y
最大割问题 设 G = ( V , E ) G=(V,E) G=(V,E) 是有 n n n 个顶点的无向图,设边 ( i , j ) (i,j) (i,j) 上的权为 w i j ( w i j = w j i ≥ 0 ) w_{ij}(w_{ij}=w_{ji}\ge 0) wij(wij=wji≥0)。图 G G G 的一个割 ( S , S ′ ) (S,S') (S,S′) 是指 n n n 个顶点上的一个分割: S ∩ S ′ = ∅ , S ∪ S ′ = V S\cap S'=\empty,S\cup S'=V S∩S′=∅,S∪S′=V。最大割问题是求一个分割 ( S , S ′ ) (S,S') (S,S′) 使连接 S S S 和 S ′ S' S′ 之间的所有边上的权最大。
设 $x_i = 1\ \text{if} \ \ i\in S,\ x_i = -1 \ \text{if} \ \ i\in S’ $,则分割 ( S , S ′ ) (S,S') (S,S′) 上的权为:
1 2 ( 1 2 ∑ i , j = 1 n w i j − 1 2 ∑ i , j = 1 n w i j x i x j ) = 1 4 ∑ i , j = 1 n w i j ( 1 − x i x j ) . \frac{1}{2}(\frac{1}{2}\sum_{i,j=1}^n w_{ij}-\frac{1}{2}\sum_{i,j=1}^n w_{ij} x_ix_j)=\frac{1}{4}\sum_{i,j=1}^n w_{ij}(1-x_ix_j). 21(21i,j=1∑nwij−21i,j=1∑nwijxixj)=41i,j=1∑nwij(1−xixj).
所以最大割问题可以表示为:
max 1 4 ∑ i , j = 1 n w i j ( 1 − x i x j ) , s . t . x ∈ { − 1 , 1 } n . \begin{aligned} &\max\ \frac{1}{4}\sum_{i,j=1}^n w_{ij}(1-x_ix_j),\\ & s.t.\ x\in \{-1,1\}^n. \end{aligned} max 41i,j=1∑nwij(1−xixj),s.t. x∈{−1,1}n.
最大割问题是组合优化中著名的NP难问题,l995年,Goemans和Williamson对
最大割问题的SDP松弛给出了一个漂亮的结果:
f o p t ≤ f S D P ≤ α f o p t , α = 1.138 ⋅ ⋅ ⋅ , f_{opt}≤f_{SDP}≤\alpha f_{opt},\alpha=1.138···, fopt≤fSDP≤αfopt,α=1.138⋅⋅⋅,
这里 f o p t f_{opt} fopt 是最大割问题的最优值, f S D P f_{SDP} fSDP是SDP松弛问题的最优值
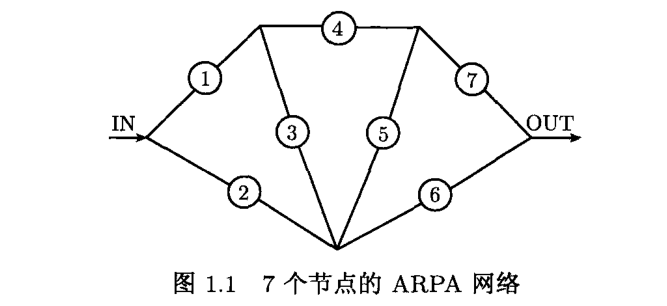
可靠性网络 考虑有 n n n 个子系统的网络.设 r i ( 0 < r i < 1 ) r_i(0<r_i<1) ri(0<ri<1) 是第 i i i 个子系统中的部件可靠性, x i x_i xi 表示第 i i i 个子系统的冗余部件的个数。网络可靠性优化问题是求最优的冗余向量 x = ( x 1 , ⋅ ⋅ ⋅ , x n ) T x=(x_1,···,x_n)^T x=(x1,⋅⋅⋅,xn)T 使网络的整体可靠性最大。
第 i i i 个子系统的可靠性为
R i ( x i ) = 1 − ( 1 − r i ) x i , i = 1 , . . . , n R_i(x_i)=1-(1-r_i)^{x_i},\ i=1,...,n Ri(xi)=1−(1−ri)xi, i=1,...,n
整个网络的可靠性 R s ( x ) R_s(x) Rs(x) 是关于 R 1 ( x 1 ) , . . . , R n ( x n ) R_1(x_1),...,R_n(x_n) R1(x1),...,Rn(xn) 的增函数,下图所示的网络的可靠性为
R s = R 6 R 7 + R 1 R 2 R 3 ( Q 6 + R 6 Q 7 ) + R 1 R 4 R 7 Q 6 ( Q 2 + R 2 Q 3 ) R_s = R_6R_7+R_1R_2R_3(Q_6+R_6Q_7)+R_1R_4R_7Q_6(Q_2+R_2Q_3) Rs=R6R7+R1R2R3(Q6+R6Q7)+R1R4R7Q6(Q2+R2Q3)
其中 Q i = 1 − R i , i = 1 , . . . , n Q_i = 1-R_i,i=1,...,n Qi=1−Ri,i=1,...,n,对应的最优冗余问题为:max R s ( x ) = f ( R 1 ( x 1 ) , . . . , R n ( x n ) ) , s . t . g i ( x ) = ∑ j = 1 n g i j ( x j ) ≤ b i , i = 1 , . . . , m , x ∈ X = { x ∈ Z n ∣ 1 ≤ l j ≤ x j ≤ u j , j = 1 , . . . , n } \begin{aligned} &\max\ R_s(x)=f(R_1(x_1),...,R_n(x_n)),\\ & s.t.\ g_i(x)=\sum_{j=1}^ng_{ij}(x_j)\le b_i,\quad i=1,...,m,\\ &\quad\quad x\in X=\{x\in \Z^n|1\le l_j\le x_j\le u_j,j=1,...,n\} \end{aligned} max Rs(x)=f(R1(x1),...,Rn(xn)),s.t. gi(x)=j=1∑ngij(xj)≤bi,i=1,...,m,x∈X={x∈Zn∣1≤lj≤xj≤uj,j=1,...,n}
其中 g i ( x ) , i = 1 , . . . , m g_i(x),i=1,...,m gi(x),i=1,...,m 代表不同的资源消耗函数,例如费用、体积、重量等。
1.2 问题的挑战性
很多整数规划问题往往看上去很简单,数学模型也不复杂,如0-1背包问题、最大割问题等,但求解这类问题其实非常困难.绝大部分整数规划问题的可行域都只有有限多个可行点(决策方案),一个简单幼稚的想法是枚举所有的可行点,但是这样会使求解难度指数增加。大部分整数规划问题的困难在于:我们本质上只能使用枚举法或隐枚举法的思想来求解问题最优解,故当问题的规模越来越大时,算法的计算时间急剧增加。与此形成对照的是连续优化问题,我们知道,最简单的连续优化问题的可行点的个数也是无穷多个,但寻找可行域中的最优点并不需要借助枚举法的思想,因为利用微积分的工具可以刻画出最优点需要满足的一组容易验证的最优性条件,如KKT条件。故只有当算法需要枚举或部分枚举这些可行点时,可行域中可行点的个数才和问题的难度有关。
另外一个朴素的想法是“四舍五入”:求解相应的连续优化问题(丢掉整数约束),然后对求得的解进行四舍五入,得到一个整数解.这个方法有两个问题:(1)一般很难通过四舍五入得到一个满足约束条件的可行解;(2)即使能求得一个可行解,其质量往往很差,即可能离最优解的距离很远,甚至和随机产生的可行解差不多。贪心算法往往可以帮助我们求到一个问题的近似解。例如,在0-1背包问题中,可以先进行排序:
c j 1 a j 1 ≥ c j 2 a j 2 ≥ . . . ≥ c j n a j n \frac{c_{j1}}{a_{j1}}\ge\frac{c_{j2}}{a_{j2}}\ge ... \ge\frac{c_{jn}}{a_{jn}} aj1cj1≥aj2cj2≥...≥ajncjn
然后按照从大到小的顺序 j 1 , . . . , j n j_1,...,j_n j1,...,jn 选取物品知道背包的容量 b b b 不能再装下一个物品。
在实际应用中提出的很多整数规划问题的规模一般都很大,直接利用现有的算法和软件求解往往是不可能的.这就促使人们研究有效快速的近似算法或启发式算法以寻找问题的一个近似最优解或较好的可行解,如近年来发展起来的基于半定规划的随机化算法和各种针对具体整数规划和组合优化问题的近似算法。
参考资料
- 整数规划 孙小玲,李瑞 北京,科学出版社 2010
- Wolsey L A. Integer programming[M]. John Wiley & Sons, 2020.
相关文章:
整数规划——第一章 引言
整数规划——第一章 引言 整数规划是带整数变量的最优化问题,即最大化或最小化一个全部或部分变量为整数的多元函数受约束于一组等式和不等式条件的最优化问题。许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模。 考虑一个电视机工厂的生产…...

C语言结构体讲解
目录 结构体的声明 结构的基础知识 结构的声明 为什么要出现结构体? 结构成员的类型 结构体变量的定义和初始化 定义:(全局变量//局部变量) 初始化: 结构体成员的访问 结构体传参 结构体的声明 结构的基础知识…...
021 - STM32学习笔记 - Fatfs文件系统(三) - 细化与总结
021 - STM32学习笔记 - Fatfs文件系统(三) - 细化与总结 上节内容中,初步实现了FatFs文件系统的移植,并且实现了设备的挂载、文件打开/关闭与读写功能,这里对上节遗留的一些问题进行总结,并且继续完善文件…...
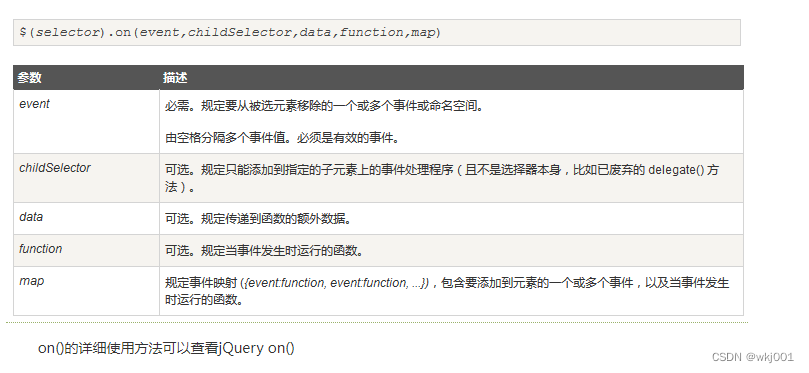
jQuery如何获取动态添加的元素
jQuery如何获取动态添加的元素 使用 on()方法 本质上使用了事件委派,将事件委派在父元素身上 自 jQuery 版本 1.7 起,on() 方法是 bind()、live() 和 delegate() 方法的新的替代品,但是由于on()方法必须有事件,没有事件时可选择de…...
Keepalived 在CentOS 7安装并配置监听MySQL双主
keepalived安装 MySQL双主配置请看这里:https://tongyao.blog.csdn.net/article/details/132016200?spm1001.2014.3001.5502 128、129两台服务器安装步骤相同,配置文件不同,下面有介绍。 1.安装相关依赖包,并下载keepalived安…...

深度学习,神经网络介绍
目录 1.神经网络的整体构架 2.神经网络架构细节 3.正则化与激活函数 4.神经网络过拟合解决方法 1.神经网络的整体构架 ConvNetJS demo: Classify toy 2D data 我们可以看看这个神经网络的网站,可以用来学习。 神经网络的整体构架如下1: 感知器&…...

中国AI大模型峰会“封神之作”!开发者不容错过这场夏季盛会
年度最强大模型顶会来袭!喊话中国数百万AI开发者,速来! 硬核来袭!中国AI大模型峰会“封神之作”,开发者们不容错过! 前瞻大模型发展趋势,紧跟这场大会! 中国科技超级碗,大模型最新前…...
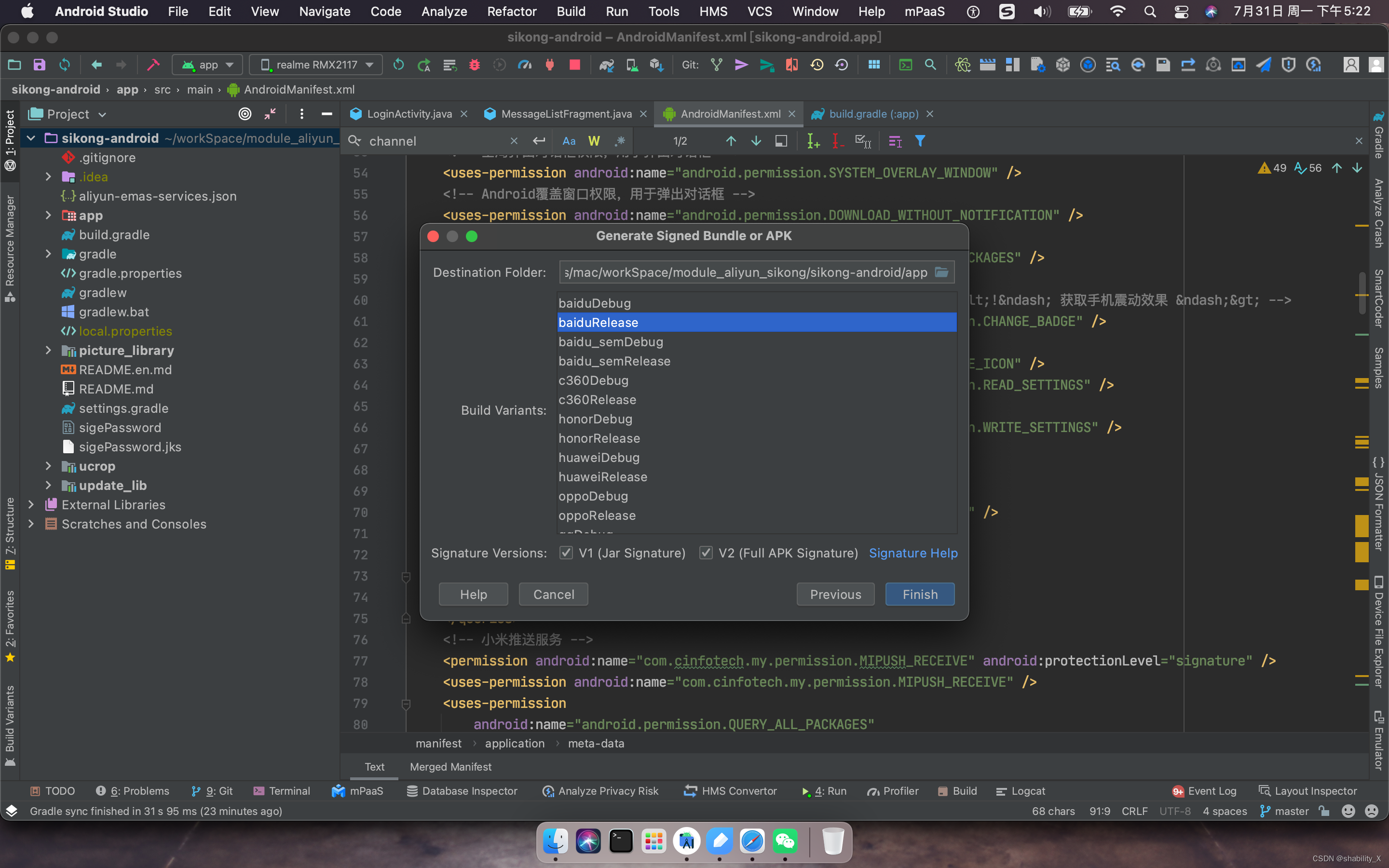
Android Studio多渠道打包
使用环境: Android studio 多渠道打包 使用方法: 1 APP下build.gradle文件 flavorDimensions "default"productFlavors {huawei {dimension "default"manifestPlaceholders [ channel:"huawei" ]}xiaomi {dimension &…...

RK3566 Android11默认客户Launcher修改
前言 客户需要默认自己的Launcher为home,同时保留系统的Launcher3. 解决办法:在启动home应用之前设置一下默认Launcher。查找home app启动相关资料,找到了frameworks/base/services/core/java/com/android/server/wm/RootWindowContainer.java的startHomeOnTaskDisplayA…...

ORB算法在opencv中实现方法
在OPenCV中实现ORB算法,使用的是: 1.实例化ORB orb cv.xfeatures2d.orb_create(nfeatures)参数: nfeatures: 特征点的最大数量 2.利用orb.detectAndCompute()检测关键点并计算 kp,des orb.detectAndCompute(gray,None)参数:…...

vue项目回显文本无法识别换行符
解决方法 1:使用<br/>替换文本中的\n,使用v-html渲染 <template> <div v-html"str"></div> </template> <script> let str 以下内容自动换行\n换行了 // 使用replace截取提换 this.str str.replace(/…...

Minio 部署
minio 官网:https://www.minio.org.cn/ 部署文档:https://www.minio.org.cn/docs/minio/container/operations/install-deploy-manage/deploy-minio-single-node-single-drive.html# 选择自己的部署环境: 我用的docker: docker pull qua…...
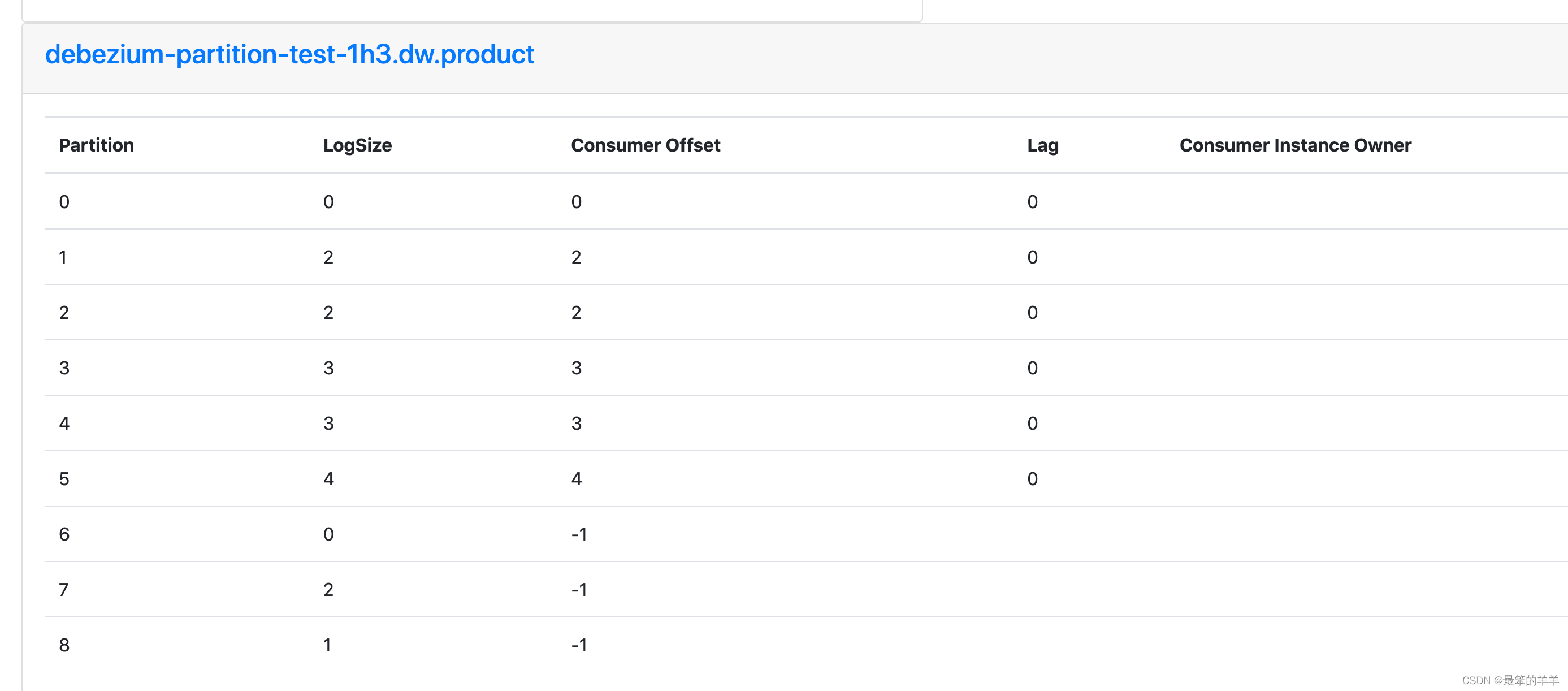
Kafka系列之:记录一次Kafka Topic分区扩容,但是下游flink消费者没有自动消费新的分区的解决方法
Kafka系列之:记录一次Kafka Topic分区扩容,但是下游flink消费者没有自动消费新的分区的解决方法 一、背景二、解决方法三、实现自动发现新的分区一、背景 生产环境Kafka集群压力大,Topic读写压力大,消费的lag比较大,因此通过扩容Topic的分区,增大Topic的读写性能理论上下…...
)
Ansible部署MariaDB galera集群(多主)
文章目录 Ansible部署MariaDB galera集群(多主)介绍节点规划基础环境准备编写剧本文件执行剧本文件查看集群状态测试 Ansible部署MariaDB galera集群(多主) 介绍 MariaDB Galera集群是一套基于同步复制的、多主的MySQL集群解决方案,使用节点没有单点故障ÿ…...

立体库-库龄
split 用法第一种: 1.对单个字符进行分割(注意这里是字符,不是字符串,故只能用单引号‘’) string sabcdeabcdeabcde; string[] sArrays.Split(c) ; foreach(string i in sArray) Console.WriteLine(i.ToString());…...

extern/头文件包含,实现一个函数被两个文件共用
目录 一、extern 1、在a.c文件中定义int add函数 2、在b.c文件中使用extern关键字声明add函数 二、用头文件包含的形式 1、在a.c文件中定义int add函数 2、创建一个名为a.h的头文件,其中包含add函数的函数原型 3、在b.c文件中包含a.c的头文件,并调…...
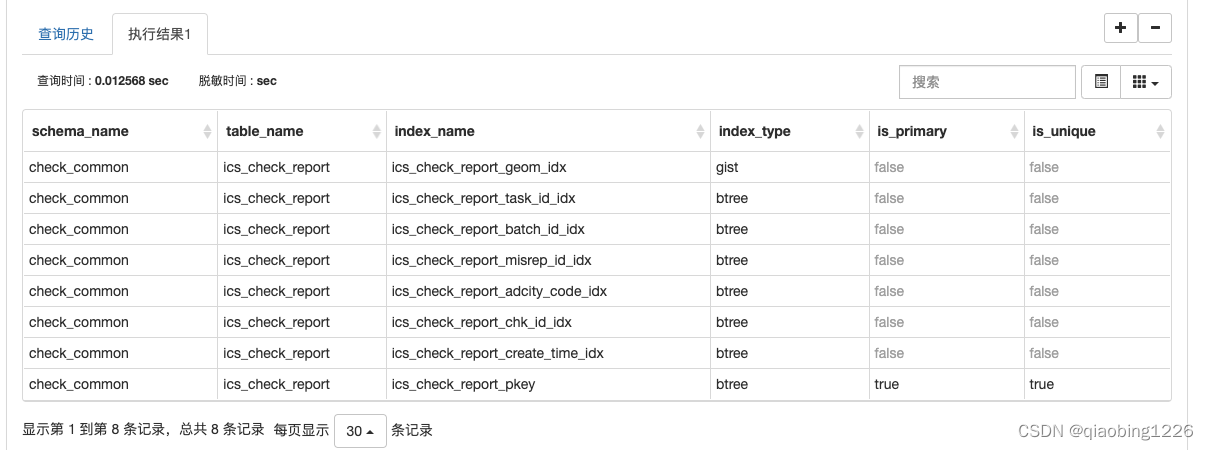
pgsql 查看某个表建立了那些索引sql
执行以下sql: SELECTns.nspname as schema_name,tab.relname as table_name,cls.relname as index_name,am.amname as index_type,idx.indisprimary as is_primary,idx.indisunique as is_unique FROMpg_index idx INNER JOIN pg_class cls ON cls.oididx.indexrel…...

【SCSS】网格布局中的动画
效果 index.html <!DOCTYPE html> <html><head><title> Document </title><link type"text/css" rel"styleSheet" href"index.css" /></head><body><div class"container">&l…...

Docker基础命令(一)
Docker使用1 一、运行终端 打开终端,输入docker images ,如果运行正常,表示docker已经可以在本电脑上使用了 二、docker常用命令 指令说明docker images查看已下载的镜像docker rmi 镜像名称:标签名删除已下载的镜像docker search 镜像从官…...

django4.2 day1Django快速入门
1、创建虚拟环境 打开cmd安装virtualenv pip install virtualenvwrapper-winworkon 查看虚拟环境mkvirtualenv 创建新的虚拟环境删除虚拟环境 rmvirtualenv 进入虚拟环境 workon env 2、创建django虚拟环境并安装django 创建虚拟环境mkvirtualenv django4env进入虚拟环境安…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
