当前位置： 首页 > news >正文

windows如何上架ios应用到app store

news 2025/12/23 1:38:12

Application Uploader iOS App上架工具是一款非常好用的针对iOS苹果应用程序软件开发的实用编程工具，它的主要作用是帮助用户进行快速的程序应用设计和程序应用调试，节省用户进行软件开发耗费的不必要时间！

​

 

编辑切换为居中

添加图片注释，不超过 140 字（可选）

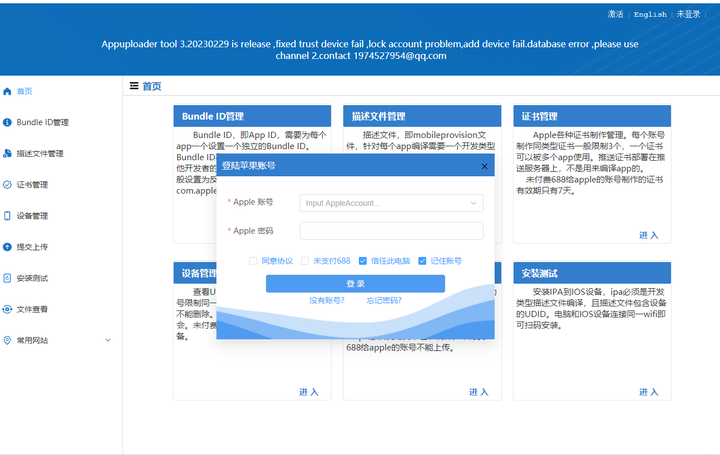
Appuploader是一个IOS开发助手，可以快速，轻松地生成ios开发证书，不需要钥匙串助手; appuploader可以批量上传屏幕截图并将ipa文件上传到Apple商店，在windows，linux或mac上，不需要应用程序加载器和mac计算机。

1、iOS证书和配置文件管理

Appuploader支持创建各种Apple证书，并且创建过程非常简单，只需输入证书名称，创建邮箱等信息即可创建证书。

2、在Windows，Linux或Mac中提交Ipa

通过appuploader，您可以在windows，mac或linux中将一个或多个ipa文件上传到appstore，故障的概率将大大降低; 通过mac中的应用程序加载器上传，并且经常上传失败的情况。 使用appuploader ipa文件，上传快速，成功率高。

3、批量上传屏幕截图和更新APP信息

提交屏幕截图到itunesconnect是一件非常麻烦的事情，不得不上传几十个屏幕截图，重复沉闷。使用appuploader上传屏幕截图可以打包上传。

4、一次更新多个IOS应用程序

使用Appuploader工具可以一次上传多个应用程序到ios appstore。

5、使用模板更新程序

使用appuploader模板更新app关键字，标题，说明，屏幕或其他应用信息更加的便捷，效率大升。

6、更新应用程序说明

一般我们只更新appstore信息描述和关键字，使用Appuploader可以使用模板进行详细更新。

​

 

编辑切换为居中

添加图片注释，不超过 140 字（可选）

相关文章：

windows如何上架ios应用到app store

Application Uploader iOS App上架工具是一款非常好用的针对iOS苹果应用程序软件开发的实用编程工具，它的主要作用是帮助用户进行快速的程序应用设计和程序应用调试，节省用户进行软件开发耗费的不必要时间！ ​ 编辑切换为居中 添加图片注释&…...

编程日记 2023/8/1 21:13:43

Hadoop学习日记-YARN组件

YARN(Yet Another Resource Negotiator)作为一种新的Hadoop资源管理器，是另一种资源协调者。 YARN是一个通用的资源管理系统和调度平台，可为上层应用提供统一的资源管理和调度 YARN架构图 YARN3大组件： （物理层面&#xff09…...

编程日记 2023/8/1 21:12:42

汽车过户时，怎么选到理想的好车牌？

在汽车过户的过程中，选到一副理想的好车牌就像买彩票中大奖一样令人兴奋。但是，怎样找到这样一块车牌呢？这就是本文要探讨的问题。 首先，我们来聊聊选车牌的技巧。很多人喜欢选择有特别数字的车牌，如“8888”、“6666”…...

编程日记 2023/8/1 21:11:41

力扣468 验证IP地址

ipv4地址：1.必须是四个非空子串 2.每个非空子串不含前导零 3.子串里字符只能是0~255 ipv6地址：1.必须是八个非空子串 2。每段非空串得长度是否在1~4之间，且不含0-9，a-f，A-F之外得字符。 3.同时0-9也不允许含前导零 cl…...

编程日记 2023/8/1 21:10:39

前端静态登录页面实现

<template> <!-- <el-button type="primary" @click="handleLogin">测试登录</el-button>--> <!-- <el-button type="danger" @click="handleUserList">测试获取用户请求</el-button>-->…...

编程日记 2023/8/1 21:09:38

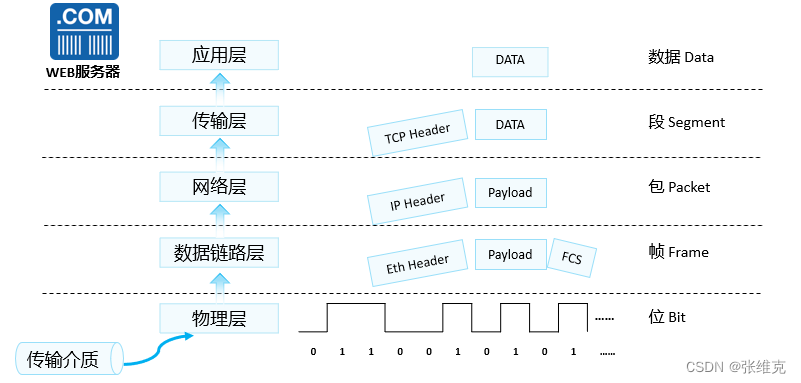
华为数通HCIA-网络参考模型（TCP/IP）

网络通信模式 作用&#xff1a;指导网络设备的通信&#xff1b; OSI七层模型&#xff1a; 7.应用层&#xff1a;由应用层协议&#xff08;http、FTP、Telnet.&#xff09;为应用程序产生对应的数据&#xff1b; 6.表示层&#xff1a;将应用层产生的数据转换成网络设备看得懂…...

编程日记 2023/8/1 21:08:37

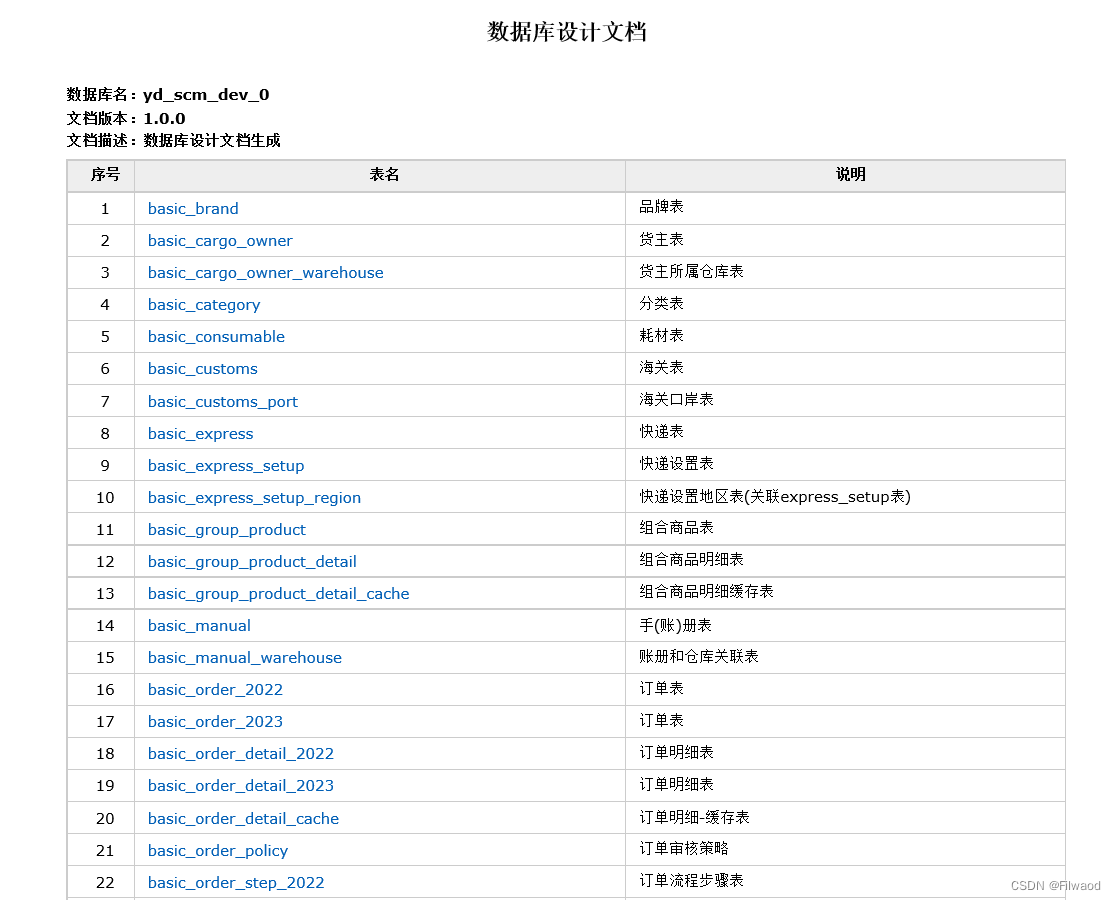
java快速生成数据库表文档（HTML、DOC、MD）

在企业级开发中、我们经常会有编写数据库表结构文档的时间付出&#xff0c;关于数据库表结构文档状态&#xff1a;要么没有、要么有、但都是手写、后期运维开发&#xff0c;需要手动进行维护到文档中&#xff0c;很是繁琐&#xff0c;这里推荐一个开源项目&#xff1a;screw gi…...

编程日记 2023/8/1 21:07:34

Dojo学习和常用知识

目录 一、Dojo 的基本概念二、Dojo 的组件和模板三、Dojo 的应用场景四、Dojo 的未来发展五、学习 Dojo 的大纲和建议&#xff1a;六、Dojo 代码示例&#xff1a; Dojo 是一个流行的 JavaScript 库&#xff0c;用于开发 Web 应用程序。它提供了许多功能&#xff0c;如 DOM 操作…...

编程日记 2023/8/1 21:06:32

媒体查询详解

引言 媒体查询是 CSS3 的一个新的技术&#xff0c;它使我们可以针对不同的设备&#xff08;或者说&#xff0c;不同的屏幕尺寸和分辨率&#xff09;来应用不同的样式。 媒体查询包含一个媒体类型和至少一个使用宽度、高度、颜色等条件限制的表达式。CSS 用于桌面电脑的屏幕可…...

编程日记 2023/8/1 21:05:28

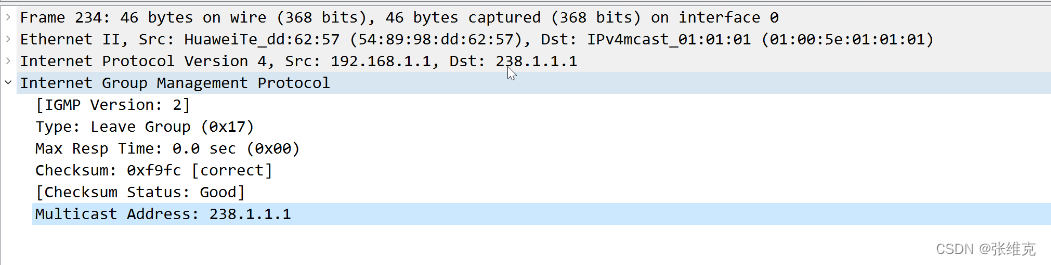
华为数通HCIP-IGMP（网络组管理协议）

IGMP&#xff08;网络组管理协议&#xff09; 作用&#xff1a;维护、管理最后一跳路由器以及组播接收者之间的关系&#xff1b; 应用&#xff1a;最后一跳路由器以及组播接收者之间&#xff1b; 原理&#xff1a;当组播接收者需要接收某个组别的流量时&#xff0c;会向最后…...

编程日记 2023/8/1 21:04:25

价格管控有哪些有效的方法

品牌在面对线上店铺的低价、窜货时&#xff0c;需要及时进行干预治理&#xff0c;否则低价效应会蔓延&#xff0c;会有越来越多的店铺跟价&#xff0c;导致渠道更加混乱&#xff0c;但是管控价格也非一时之事&#xff0c;需要品牌按流程治理。 力维网络有多年价格管控经验&…...

编程日记 2023/8/1 21:03:24

【Docker】Docker相关基础命令

目录 一、Docker服务相关命令 1、启动docker服务 2、停止docker服务 3、重启docker服务 4、查看docker服务状态 5、开机自启动docker服务 二、Images镜像相关命令 1、查看镜像 2、拉取镜像 3、搜索镜像 4、删除镜像 三、Container容器相关命令 1、创建容器 2、查…...

编程日记 2023/8/1 21:02:22

掌握Python的X篇_16_list的切片、len和in操作

接上篇掌握Python的X篇_15_list容器的基本使用&#xff0c;本篇进行进一步的介绍。 文章目录 1. list的索引下标可以是负数2. 切片&#xff08;slice&#xff09;2.1 切片基础知识2.2 如何“取到尽头”2.3 按照步长取元素2.4 逆序取值 3. len函数获取lis的元素个数4. in操作符…...

编程日记 2023/8/1 21:01:12

给定长度值length，把列表切分成每段长度为length的N段列表，Kotlin

给定长度值length&#xff0c;把列表切分成每段长度为length的N段列表&#xff0c;Kotlin import kotlin.random.Randomfun main(args: Array<String>) {var source mutableListOf<String>()val end Random.nextInt(30) 1for (i in 0 until end) {source.add(i.…...

编程日记 2023/8/1 21:00:11

leetcode每日一题Day2——344. 反转字符串

✨博主&#xff1a;命运之光 &#x1f984;专栏&#xff1a;算法修炼之练气篇&#xff08;C\C版&#xff09; &#x1f353;专栏&#xff1a;算法修炼之筑基篇&#xff08;C\C版&#xff09; &#x1f433;专栏&#xff1a;算法修炼之练气篇&#xff08;Python版&#xff09; …...

编程日记 2023/8/1 20:59:09

ISP记1

噪声分类 空间区域 分布模型分类&#xff1a;Gaussian噪声、瑞利噪声、泊松噪声、乘性噪声、脉冲噪声、均匀分布噪声 频域谱波形分类&#xff1a;均匀分布噪声、白噪声&#xff08;噪声的功率谱为参数&#xff0c;且与图像线性无关&#xff09;1/f噪声、a f 2 f^{2} f2噪声&a…...

编程日记 2023/8/1 20:58:08

无线蓝牙耳机有什么值得耳机买的？几款值得买的口碑品牌盘点

蓝牙耳机是一种无线耳机&#xff0c;其通过蓝牙技术与其他设备进行连接&#xff0c;例如手机、电脑、平板电脑等。蓝牙耳机使得用户可以在不受线缆限制的情况下享受音频体验&#xff0c;而且还可以方便地进行通话&#xff0c;目前市场上有许多不同种类和品牌的蓝牙耳机&#xf…...

编程日记 2023/8/1 20:57:07

异步检索在 Elasticsearch 中的理论与实践

异步检索在 Elasticsearch 中的理论与实践 https://www.elastic.co/guide/en/elasticsearch/reference/8.1/async-search.html#submit-async-search 引言 Elasticsearch 是一种强大的分布式搜索和分析引擎&#xff0c;它能够快速地存储、搜索和分析大量数据。在处理大规模数据时…...

编程日记 2023/8/1 20:56:05

了解Unity编辑器之组件篇Physics 2D（十二）

一、Area Effector 2D区域施加力&#xff09;&#xff1a;用于控制区域施加力的行为 Use Collider Mask&#xff08;使用碰撞器遮罩&#xff09;&#xff1a;启用后&#xff0c;区域施加力仅会作用于特定的碰撞器。可以使用Collider Mask属性选择要作用的碰撞器。 Collider Ma…...

编程日记 2023/8/1 20:55:04

[Pytorch]手写数字识别——真·手写！

Github网址&#xff1a;https://github.com/diaoquesang/pytorchTutorials/tree/main 本教程创建于2023/7/31&#xff0c;几乎所有代码都有对应的注释&#xff0c;帮助初学者理解dataset、dataloader、transform的封装&#xff0c;初步体验调参的过程&#xff0c;初步掌握openc…...

编程日记 2023/8/1 20:54:03

超短脉冲激光自聚焦效应

前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应&#xff0c;这是一种非线性光学现象&#xff0c;主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场&#xff0c;对材料产生非线性响应&#xff0c;可能…...

编程新知 2025/12/22 12:57:23

【WiFi帧结构】

文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成&#xff1a;MAC头部frame bodyFCS&#xff0c;其中MAC是固定格式的&#xff0c;frame body是可变长度。 MAC头部有frame control&#xff0c;duration&#xff0c;address1&#xff0c;address2&#xff0c;addre…...

编程新知 2025/12/20 3:36:01

Go 语言接口详解

Go 语言接口详解 核心概念 接口定义 在 Go 语言中&#xff0c;接口是一种抽象类型&#xff0c;它定义了一组方法的集合&#xff1a; // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的&#xff1a; // 矩形结构体…...

编程新知 2025/12/22 12:07:54

Qt Http Server模块功能及架构

Qt Http Server 是 Qt 6.0 中引入的一个新模块&#xff0c;它提供了一个轻量级的 HTTP 服务器实现&#xff0c;主要用于构建基于 HTTP 的应用程序和服务。 功能介绍&#xff1a; 主要功能 HTTP服务器功能&#xff1a; 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

编程新知 2025/10/17 21:16:57

Neo4j 集群管理：原理、技术与最佳实践深度解析

Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...

编程新知 2025/12/11 3:51:27

Ascend NPU上适配Step-Audio模型

1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统&#xff0c;支持多语言对话&#xff08;如 中文&#xff0c;英文&#xff0c;日语&#xff09;&#xff0c;语音情感&#xff08;如 开心&#xff0c;悲伤&#xff09;&#x…...

编程新知 2025/12/16 0:36:19

【RockeMQ】第2节｜RocketMQ快速实战以及核⼼概念详解（二）

升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点&#xff0c;但无自动故障转移能力&#xff0c;Master宕机后需人工切换&#xff0c;期间消息可能无法读取。Slave仅存储数据&#xff0c;无法主动升级为Master响应请求&#xff…...

编程新知 2025/9/2 3:37:40

RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程

本文较长&#xff0c;建议点赞收藏&#xff0c;以免遗失。更多AI大模型应用开发学习视频及资料&#xff0c;尽在聚客AI学院。 本文全面剖析RNN核心原理&#xff0c;深入讲解梯度消失/爆炸问题&#xff0c;并通过LSTM/GRU结构实现解决方案&#xff0c;提供时间序列预测和文本生成…...

编程新知 2025/12/19 21:20:28

Pinocchio 库详解及其在足式机器人上的应用

Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库&#xff0c;专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性&#xff0c;并提供了一个通用的框架&…...

编程新知 2025/11/28 5:32:31

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2025/12/10 5:35:21