【暑期每日一练】 day11
目录
选择题
(1)
解析:
(2)
解析:
(3)
解析:
(4)
解析:
(5)
解析:
编程题
题一
描述
示例
提示
解析 :
代码实现
题二
描述
输入描述:
输出描述:
示例
解析:
代码实现
总结
选择题
(1)
1、声明以下变量,则表达式: ch/i + (f*d – i) 的结果类型为( )
char ch;
int i;
float f;
double d;A: char B: int C: float D: double
答案:D
解析:
基本数据类型的等级从低到高如下:char int long float double运算的时候是从低转到高的,表达式的类型会自动提升或者转换为参与表达式求值的最上级类型
(2)
2、关于代码的说法正确的是( )
#include <stdio.h>
int main()
{int x = -1;unsigned int y = 2;if (x > y){printf("x is greater");} else{printf("y is greater");} return 0;
}A: x is greater B: y is greater C: 依赖实现 D: 随机
答案:A
解析:
x是有符号数-1,内存中是全1,当有符号的x和无符号数进行比较时,x会隐式类型转换被当做无符号数,是一个很大的数,这时就选择A了
(3)
3、已知有如下各变量的类型说明,则以下不符合C语言语法的表达式是( )
int k, a, b;
unsigned int w = 5;
double x = 1.42;A: x%3 B: w+=-20 C: k=(a=200,b=300) D: a+=a-=a=9
答案:A
解析:
A选项,取余操作两边必须是整数
(4)
4、下面函数的输出结果是( )
void func()
{int k = 1^(1 << 31 >> 31);printf("%d\n", k);
}A: 0 B: -1 C: -2 D: 1
答案:C
解析:
(1 << 31 );左移31位,并在右侧填充0,得到0x80000000,即符号位为1,其他为0,即-2147483648
int k = 1^(1 << 31 >> 31);注意,这里在右移的时候,符号位保持为1,右移后填充1,结果为0xFFFFFFFF,即-1,0x00000001^0xFFFFFFFF,即0xFFFFFFFE(-2)
(5)
5、如下代码的输出结果是( )
#include <stdio.h>
int main()
{int i = 1;sizeof(i++);printf("%d\n", i);return 0;
}A: 1 B: 4 C: 2 D: 8
答案:A
解析:
一般表达式的运算是在运行时执行的,而sizeof是一个编译阶段就执行的运算符,在其内的任何运算都不执行,只推测出其中表达式结果的类型求其大小,故前后i的值不变。
编程题
题一
描述
给定一个二进制数组 nums , 计算其中最大连续 1 的个数
示例

提示
解析 :
这道题思路比较简单,统计连续1的个数,遇到0时表示连续中断,判断如果当前的统计数大于之前最大的则替换,然后继续下一个位置开始的统计即可。
代码实现
int findMaxConsecutiveOnes(int* nums, int numsSize)
{int max_count = 0, cur_size = 0;;for (int i = 0; i < numsSize; i++) {if (nums[i] == 1) {cur_size++;}else {max_count = max_count > cur_size ? max_count : cur_size;cur_size = 0;}}max_count = max_count > cur_size ? max_count : cur_size;return max_count;
}题二
描述
完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。
它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。
例如:28,它有约数1、2、4、7、14、28,除去它本身28外,其余5个数相加,1+2+4+7+14=28。
输入n,请输出n以内(含n)完全数的个数。
数据范围: 1≤n≤5×105
输入描述:
输入一个数字n
输出描述:
输出不超过n的完全数的个数
示例

解析:
这道题的关键在于完全数的判断:完全数指的是一个数字的所有约数的和和自身相等。我们只需要从 1 开始将这个数的约数相加求和即可。
约数就是能够被数字整除,而这里简化的一个思路是数字能够被整除,则除数和结果就都是约数,这种思路下,只需要从1计算到平方根即可
比如:数字 8 , 能够整除 2 ,结果是 4 ,则除数 2 和结果 4 都是约数,而这两个只需要一次计算判断即可。
需要注意的是 4,9,25... 这种,除数和结果相同的情况,则除数或者结果只相加一次就够了。
代码实现
#include <stdio.h>
#include <math.h>
int is_perfect_num(int num) {int sum = 1;for (int i = 2; i <= sqrt(num); i++) {if (num % i ==0) {//判断是否能够整除i,能整除则i和结果都是约数sum += i; //与除数相加if (i != sqrt(num))//防止除数和结果相同的情况下重复相加sum += num / i; //与相除结果相加}}if(sum == num) return 1;return 0;
}
int main()
{int n;while (~scanf("%d", &n)) {int count = 0;for (int i = 2; i <= n;i++) { //对n以内的数字都进行判断是否是完全数,注意1不参与判断if (is_perfect_num(i)) count++;}printf("%d\n", count);} return 0;
}总结
关于今日练习讲解到这儿,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下。
相关文章:

【暑期每日一练】 day11
目录 选择题 (1) 解析: (2) 解析: (3) 解析: (4) 解析: (5) 解析: 编程题 题一 描…...

神经概率语言模型
本文主要参考《A Neural Probabilistic Language Model》这是一篇很重要的语言模型论文,发表于2003年。主要贡献如下: 提出了一种基于神经网络的语言模型,是较早将神经网络应用于语言模型领域的工作之一,具有里程碑意义。采用神经网络模型预测下一个单词…...

什么是shadow DOM?
Shadow DOM(影子DOM)是一种用于在Web组件中封装HTML、CSS和JavaScript的技术。它是Web组件的一个重要特性,旨在将组件的结构、样式和行为封装在一个独立的、隔离的DOM树中,从而与主文档的DOM树相互隔离。 传统的Web开发中&#x…...

我的 365 天创作纪念日
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...

spark-sql : “java.lang.NoSuchFieldError: out“ 异常解决
异常现象 at java.lang.reflect.Method.invoke(Method.java:498)at org.apache.spark.deploy.JavaMainApplication.start(SparkApplication.scala:52)at org.apache.spark.deploy.SparkSubmit.org$apache$spark$deploy$SparkSubmit$$runMain(SparkSubmit.scala:847)at org.apac…...
以及详细解析)
Node.js入门笔记(包含源代码)以及详细解析
Node.js 入门笔记源码 01、如何在终端中执行js 文件 目标:将下面的代码语句在中断中执行 代码演示: console.log(Hello World)for (let i 0;i < 3;i) {console.log(6)}方法:在文件上右击打开在终端中执行,然后输入node空格 输…...

windows自动化点击大麦app抢购、捡漏,仅支持windows11操作系统
文章目录 必要条件程序运行必要条件 确保windows11版本操作系统,如果不是可以通过镜像升级为windows11如果已经是windows11操作系统,确保更新到最新版本 修改系统所在时区,将国家或地区改为美国 开启虚拟化 勾选Hyper-V,如果没有则不需要勾选 勾选虚拟机平台 勾选完毕,点…...

vue 拦截 v-html 中 a 标签 href 跳转
记录 template 中 给需要 拦截的 代码片段加上click 方法 click“targetNodeNameClick” <p class"message-content message-content-text" v-html"replaceURLWithHTMLLinks(getText(message))" click"targetNodeNameClick"></p>然…...

分布式id、系统id、业务id以及主键之间的关系
推荐 连分布式ID都理解不了,你是刚培训出来冒充面试官的吧 1 分布式id、系统id、业务id以及主键之间的关系 分布式ID、系统ID、业务ID和主键的关系: 分布式ID:在分布式系统中,由于存在多个独立的节点,为了保证每个节…...
)
设计模式七:适配器模式(Adapter Pattern)
适配器模式(Adapter Pattern)是一种结构型设计模式,用于将一个类的接口转换成客户端所期望的另一个接口。它允许不兼容的接口能够协同工作。 适配器模式涉及角色: 目标接口(Target Interface):…...

数据结构---队列
(一)队列之基础补充 队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。 —— 百科 「队列 Queue」是一种…...

chatGPT在软件测试中应用方式有哪些?
ChatGPT可以在软件测试中以以下方式应用: 1. 自动化对话测试:ChatGPT可以用于自动化对话测试,模拟用户与软件系统进行实时对话。它可以扮演用户的角色,向系统发送各种类型的指令和请求,并验证系统的响应是否符合预期。…...

chatgpt 接口使用(一)
使用api实现功能 参考链接:https://platform.openai.com/examples 安装库: pip3 install openai 例如: import os import openaiopenai.api_key os.getenv("OPENAI_API_KEY") response openai.ChatCompletion.create(model&q…...

【个人笔记】Linux 服务管理两种方式service和systemctl
service命令与systemctl 命令 service 命令与传统的 SysVinit 和 Upstart 初始化系统相关。较早期的 Linux 发行版(如早期的 Ubuntu、Red Hat 等)使用了这些初始化系统。service 命令用于启动、停止、重启和查询系统服务的状态。虽然许多现代 Linux 发行…...
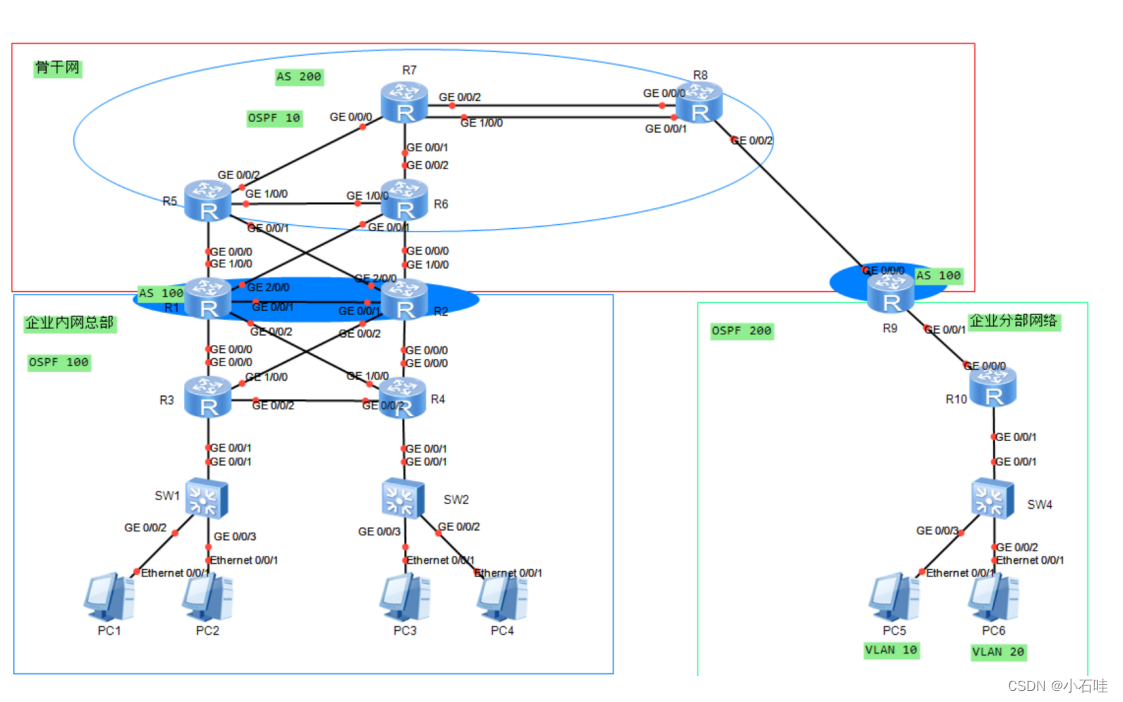
HCIP中期考试实验
考试需求 1、该拓扑为公司网络,其中包括公司总部、公司分部以及公司骨干网,不包含运营商公网部分。 2、设备名称均使用拓扑上名称改名,并且区分大小写。 3、整张拓扑均使用私网地址进行配置。 4、整张网络中,运行OSPF协议或者BGP…...
WebRTC的混音处理)
【WebRTC---源码篇】(二十二)WebRTC的混音处理
音频混音主力 音频混音主体主要通过(重采样) + (混音)为主 音频重采样 内容实现是在webrtc::voe中实现的,下面来对重采样全流程逐一分析 。 void RemixAndResample(const AudioFrame& src_frame,//源音频数据帧PushResampler<int16_t>* resampler,//重采样对…...

MTK system_server 卡死导致手机重启案例分析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、MTK AEE Log分析工具二、AEE Log分析流程三、system_server 卡死案例分析及解决 本文主要针对 Exception Type: system_server_watchdog , system_…...

加强 Kubernetes 能力:利用 CRD 定义多版本资源的实现方式
姚灿武,Rancher 中国研发工程师,拥有 7 年云计算领域经验,热衷开源技术,在云原生相关技术领域拥有丰富的开发和实践经验。 CRD,即自定义资源定义(Custom Resource Definition),是 Ku…...

区块链应用 DApp 开发需要掌握的技能
文章目录 前言为什么要开发 DAppDApp 的优势DApp 应用范围DApp 开发者技能 前言 前面区块链系列的文章中介绍了区块链技术、智能合约、web3js,Solidity 编程语言,在开发者的角度就是要基于这些知识在Web3时代去开发一个 DApp(去中心化应用程…...

关于新版本selenium定位元素报错:‘WebDriver‘ object has no attribute ‘find_element_by_id‘等问题
由于一段时间没有使用Selenium,当再次使用时发现之前写的Selenium元素定位的代码运行之后会报错,发现是Selenium更新到新版本(4.x版本)后,以前的一些常用的代码的语法发生了改变,当然如果没有更新过或是下载…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
