C语言每日一题:10.不使用+-*/实现加法+找到所有数组中消失的数。
题目一:
题目链接:
思路一:
1.两个数二进制之间进行异或如果不产生进位操作那么两个数的和就是就是两个数进行异或的结果。
举例:5(0101)2(0010)进行异或等于:7(0111)相同为0,不同位1.
2.如果两个数之间需要进位
1.如果两个1进行异或那么这个位置就变成了0满足进位的条件。(对于两个数异或求非进位和来说)。
2.只有两个1才是进位,所以使用与的方法获取要进的位之后进行左移动。(得到进位之后的数值)。
3.进行相加,但是不可以使用加法。因为我们知道两个数之间如果不产生进位操作,按位异或就是他们的和。
4.循环判断按位与的结果为0的时候说明两个数相加不存在进位。
int Add(int num1, int num2 ) {// write code hereint sum, forward;do{//1.每一个位置相加,不产生进位(10(1010)+2(0010)-->8(1000)不进位)sum = num1^num2;//2.找到要加的进位数(10(1010)&2(0010)-->2(0010)<<1-->4(0100))forward = (num1&num2) << 1;//3.将前两步的值相加,但是相加不能用加法,重复前面两个步骤,直到不产生进位num1 = sum;//第二步的forward值为0,说明没有位需要前进,它们的和必然是sum的值num2 = forward;} while (num2 != 0);//结束条件是不产生进位return num1;
}
题目二

题目链接:
>思路一:
1.使用双for循环判断。
2.从1到n循环遍历,每一个数在数组中从前到后去判断。是否存在
3.如果数组被遍历完全动没有相等的值那么说明这个外面循环的这个数不存在于数组中。
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){int n = numsSize;int* num = (int*)calloc(n,sizeof(int));int count = 0;int j = n;int flag = 0;for (int i = 1; i <= n; i++){int j = 0;for (j = 0,flag=0; j < n; j++){if ((nums[j])==i ){flag = 1;break;}}if (flag!=1){(*(num+count)) = i;count++;flag = 0;}}(*returnSize) = count;return num;
}
产生问题:
>思路二:
0.进行快速排序使nums先有序
1.不允许开辟额外的空间,因为有连续的数值存在。
2.从nums找出单独的数放到num中,并记录个数为count。
3.把num的内容拷贝到nums中。num的前面count个元素置为空
4.这个时候满足[1,n]中存在的数只有一个在nums中。
5.从1到n开始遍历,nums数组。
6.当nums的最后一个不是n就需要有一个k<=n的一个判断条件如果没有的化(n2是nums中单个数的元素个数)[num[n2-1],n]这些数值是会失去找不到的。
int cmp(void*p1,void*p2){return (*((int*)p1))-(*((int*)p2));}
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){int n = numsSize;int* num = (int*)calloc(n,sizeof(int));int count = 0;qsort(nums,n,sizeof(int),cmp);//1.从前面到后面只有一个数按照顺序放到num里面。num[count]=nums[0];count++;for(int i=0;i<n-1;i++){if(nums[i+1]!=num[count-1]){num[count]=nums[i+1];count++;}}//2.把只有一个的数放回去到nums中,把num置为空。int n2=count;count=0;memcpy(nums,num,sizeof(int)*n2);memset(num,0,sizeof(int)*n2);//3.当nums的最后一个不是n就需要有一个k<=n//的一个判断条件如果没有的化[num[n2-1],n]这些数值是会失去找不到的。int j=0;int k=1;//1,1,2,2,这样的情况。//1,2,有k<=n否则是否出现这样的情况导致有的数没有判断到。while(j<n2||k<=n){if(nums[j]==k){k++;j++;}else{num[count++]=k;k++;}}(*returnSize) = count;return num;
}
相关文章:

C语言每日一题:10.不使用+-*/实现加法+找到所有数组中消失的数。
题目一: 题目链接: 思路一: 1.两个数二进制之间进行异或如果不产生进位操作那么两个数的和就是就是两个数进行异或的结果。 举例:5(0101)2(0010)进行异或等于:7…...
LibreSSL SSL_connect: SSL_ERROR_SYSCALL in connection to github.com:443
1、问题: https://github.com/CocoaPods/Specs.git/:LibreSSL SSL_connect: SSL_ERROR_SYSCALL in connection to github.com:443的解决办法 出现这个问题的原因基本都是代理的问题: 只需要加上代理就可以了: #http代理 git conf…...

JS数组的详解与使用
什么是数组? 数组是一种有序的集合,有长度和索引,以及身上有许多的API方法 面试题:数组和伪数组的区别:数组和伪数组都有长度和索引,区别是数组身上有许多的API方法 而伪数组身上不存在这些API方法创建数组…...

c++ / python / java / PHP / SQL / Ruby / Objective-C / JavaScript 发展史
c发展史 C是由丹尼斯里奇和肯汤普森在1970年代早期开发的C语言的扩展。C最初被称为“C with Classes”,是在1980年代初期由比雅尼斯特劳斯特鲁普开发的。 1983年,斯特劳斯特鲁普将C with Classes重新命名为C。在1985年,C编译器的第一个版本被…...

Linux第一个小程序-进度条(缓冲区概念)
1.\r和\n C语言中有很多字符 a.可显字符 b.控制字符 对于回车其实有两个动作,首先换行,在将光标指向最左侧 \r :回车 \n:换行 下面举个例子: 把\n去掉会怎样 什么都没输出。为什么? 2.缓冲区概念 观察下两个…...
CentOS7环境安装tomcat
环境准备 由于是在练习,为了方便,我们可以 1.关闭防火墙 systemctl disable firewalld.service systemctl stop firewalld.service 2.关闭selinux 在/etc/selinux/config中,设置: SELINUXdisabled 3.准备jdk---》jdk-8u333-li…...

C# 中使用ValueTask优化异步方法
概要 我们在开发过程中,经常使用async的异步方法,但是有些时候,异步的方法中,可能包含一些同步的处理。本文主要介绍通过ValueTask这个struct,优化异步处理的方法性能。 代码及实现 有些时候我们会缓存一些数据在内…...

KVM创建新的虚拟机(图形化)
1.启动kvm管理器 [rootlocalhost ~]# virt-manager2.点击创建虚拟机 3.选择所需os安装镜像 4.选择合适的内存大小和CPU 5.创建所需磁盘 6.命名创建的虚拟机...

正则表达式在格式校验中的应用以及包装类的重要性
文章目录 正则表达式:做格式校验包装类:在基本数据类型与引用数据类型间的桥梁总结 在现代IT技术岗位的面试中,掌握正则表达式的应用以及理解包装类的重要性是非常有益的。这篇博客将围绕这两个主题展开,帮助读者更好地面对面试挑…...

Docker使用之java项目工程的部署
同样本文的基础建立在已在目标服务器(以linux为示例)上安装了docker,安装教程请移步度娘 若容器存在请先停止,在删除,然后删除镜像重新编译 //停止容器 sudo docker stop datatransfer//删除容器 sudo docker rm dat…...
3ds Max如何进行合成的反射光泽通道渲染
推荐: NSDT场景编辑器 助你快速搭建可二次开发的3D应用场景 1. 准备场景 步骤 1 打开 3ds Max。smart_phone.max打开已 随教程提供。 打开 3ds Max 步骤 2 按 M 打开材质编辑器。选择空材料 槽。单击漫射通道。它将打开材质/贴图浏览器窗口。选择位图࿰…...

114、Spring AOP是如何实现的?它和AspectJ有什么区别?
Spring AOP是如何实现的?它和AspectJ有什么区别? 一、AOP的理解1、spring aop:动态代理实现2、spring aop 和 AspectJ的区别3、小图一、AOP的理解 其实,AOP只是一种编程思想,表示面向切面编程,如果想实现这种思想,可以使用动态代理啊,第三方的框架 AspectJ啊等等。 1…...

正则表达式速通
简介 正则表达式,我们可以看作通配符的增强版,可以帮我们匹配指定规则的字符串,在计算机中应用广泛,比如说爬虫、网站的登录表单等。 原视频:https://www.bilibili.com/video/BV1da4y1p7iZ 学习正则表达式的常用工具…...
数据可视化(5)热力图及箱型图
1.热力图 #基本热力图 #imshow(x) #x,数据 x[[1,2],[3,4],[5,6],[7,8],[9,10]] plt.imshow(x) plt.show() #使用热力图分析学生的成绩 dfpd.read_excel(学生成绩表.xlsx) #:表示行号 截取数学到英语的列数 xdf.loc[:,"数学":英语].…...

React 组件通信-全面解析
父子组件通信 // 导入 import { useState } from "react";import "./App.scss"; import { defaultTodos } from "./components/module/contentData";// 子组件 const Module ({ id, done, text, onToggle, onDelData }) > {return (<div…...

“深入理解Spring Boot:快速构建微服务架构的利器“
标题:深入理解Spring Boot:快速构建微服务架构的利器 摘要:Spring Boot是一种基于Spring框架的开源项目,它通过自动化配置和约定优于配置的原则,使得开发者能够快速构建微服务架构。本文将深入介绍Spring Boot的特点和…...

SpringBoot超级详解
1.父工程的父工程 在父工程的父工程中的核心依赖,专门用来版本管理的 版本管理。 2.父工程 资源过滤问题,都帮解决了,什么配置文件,都已经配置好了,资源过滤问题是帮助,过滤解决让静态资源文件能够过滤到…...
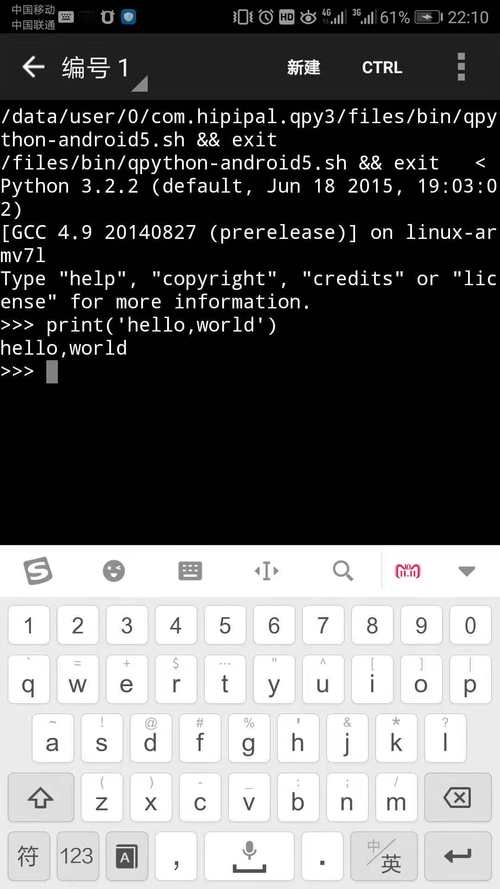
手机的python怎么运行文件,python在手机上怎么运行
大家好,小编来为大家解答以下问题,手机上的python怎么运行程序,手机的python怎么运行文件,今天让我们一起来看看吧! 1、python程序怎么在手机上运行 python语言应用很广泛,自己也很喜欢使用它,其…...
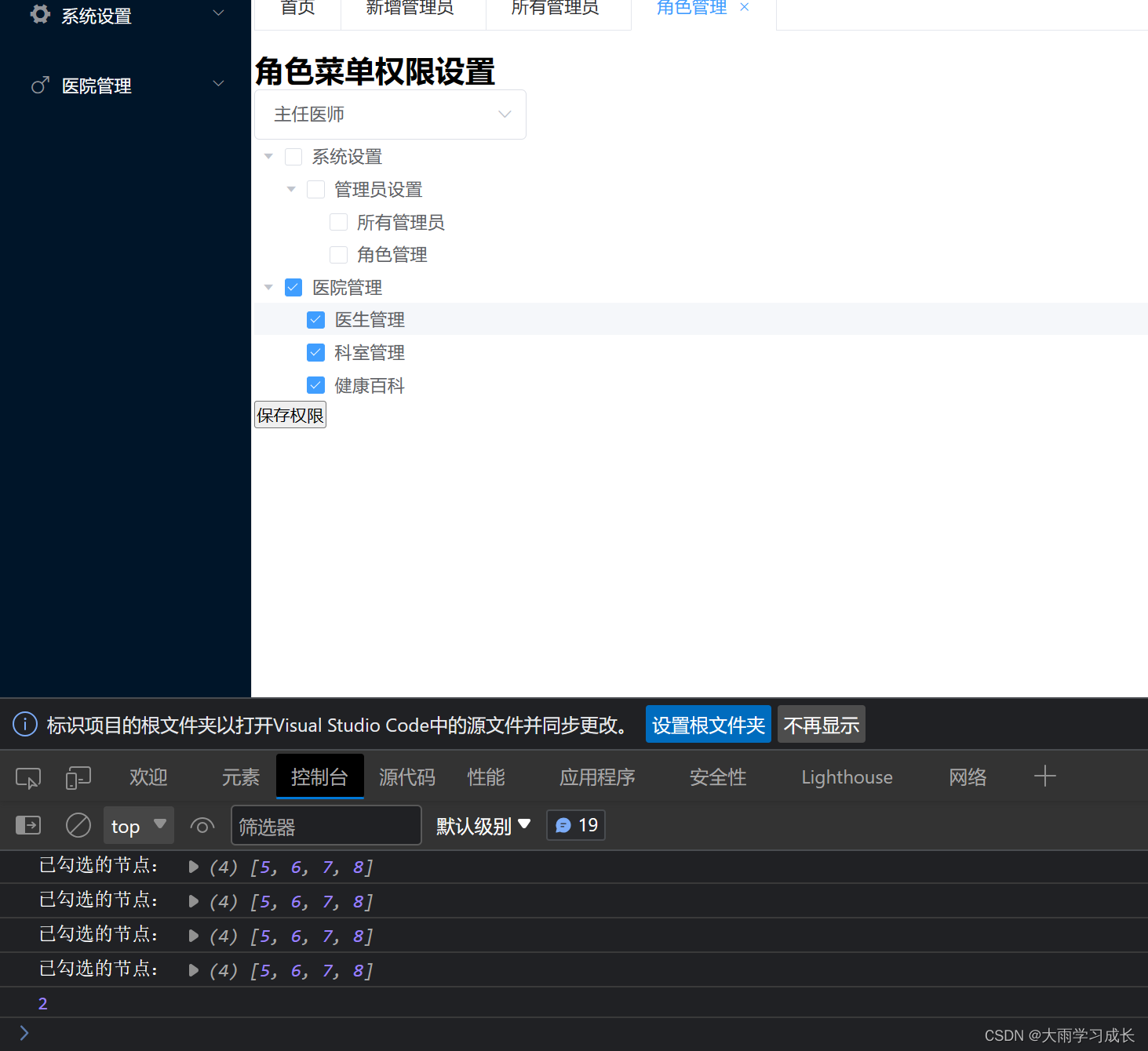
RBAC三级树状菜单实现(从前端到后端)未完待续
1、表格设计 RBAC 2、前端路由 根据不同的用户id显示不同的菜单。 根据路由 3、多级菜单 展示所有权限,并且根据当前用户id展示它所属的角色的所有菜单。 前端树状展示 思路: 后端:传给前端map,map里1个是所有菜单&am…...

牛客网Verilog刷题——VL41
牛客网Verilog刷题——VL41 题目答案 题目 请设计一个可以实现任意小数分频的时钟分频器,比如说8.7分频的时钟信号,注意rst为低电平复位。提示:其实本质上是一个简单的数学问题,即如何使用最小公倍数得到时钟周期的分别频比。设小…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

生信服务器 | 做生信为什么推荐使用Linux服务器?
原文链接:生信服务器 | 做生信为什么推荐使用Linux服务器? 一、 做生信为什么推荐使用服务器? 大家好,我是小杜。在做生信分析的同学,或是将接触学习生信分析的同学,<font style"color:rgb(53, 1…...
