算法训练营第五十六天||● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 编辑距离总结篇
● 583. 两个字符串的删除操作
这道题涉及到两个字符串删除操作,注意递推公式,理解不到位,需要再次做
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
- 确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
- dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
class Solution {
public:int minDistance(string word1, string word2) {//dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。vector<vector<int>> dp(word1.size()+1,vector<int> (word2.size()+1,0));for(int i = 0;i<word1.size()+1;i++){dp[i][0]= i;}for(int j = 0;j<word2.size()+1;j++){dp[0][j] = j;}for(int i = 1;i<=word1.size();i++){for(int j = 1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]){dp[i][j] = dp[i-1][j-1];}else{dp[i][j] = min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));}}}return dp[word1.size()][word2.size()];}
};● 72. 编辑距离
这道题和之前讲的三四道题类似,都是一步一步递增的,之后需要继续看
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1,0));for(int i = 0;i<=word1.size();i++) dp[i][0] = i;for(int j = 0;j<=word2.size();j++) dp[0][j] = j;for(int i = 1;i<=word1.size();i++){for(int j = 1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]){dp[i][j] = dp[i-1][j-1];}else{dp[i][j] = min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;}}}return dp[word1.size()][word2.size()];}
};● 编辑距离总结篇
1.判断子序列
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];2.不同的子序列
if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {dp[i][j] = dp[i - 1][j];
}3.两个字符串的删除操作
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
} else {dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}4.编辑距离
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
}
else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}相关文章:

算法训练营第五十六天||● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 编辑距离总结篇
● 583. 两个字符串的删除操作 这道题涉及到两个字符串删除操作,注意递推公式,理解不到位,需要再次做 确定dp数组(dp table)以及下标的含义 dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾…...
C语言每日一题:10.不使用+-*/实现加法+找到所有数组中消失的数。
题目一: 题目链接: 思路一: 1.两个数二进制之间进行异或如果不产生进位操作那么两个数的和就是就是两个数进行异或的结果。 举例:5(0101)2(0010)进行异或等于:7…...
LibreSSL SSL_connect: SSL_ERROR_SYSCALL in connection to github.com:443
1、问题: https://github.com/CocoaPods/Specs.git/:LibreSSL SSL_connect: SSL_ERROR_SYSCALL in connection to github.com:443的解决办法 出现这个问题的原因基本都是代理的问题: 只需要加上代理就可以了: #http代理 git conf…...

JS数组的详解与使用
什么是数组? 数组是一种有序的集合,有长度和索引,以及身上有许多的API方法 面试题:数组和伪数组的区别:数组和伪数组都有长度和索引,区别是数组身上有许多的API方法 而伪数组身上不存在这些API方法创建数组…...

c++ / python / java / PHP / SQL / Ruby / Objective-C / JavaScript 发展史
c发展史 C是由丹尼斯里奇和肯汤普森在1970年代早期开发的C语言的扩展。C最初被称为“C with Classes”,是在1980年代初期由比雅尼斯特劳斯特鲁普开发的。 1983年,斯特劳斯特鲁普将C with Classes重新命名为C。在1985年,C编译器的第一个版本被…...

Linux第一个小程序-进度条(缓冲区概念)
1.\r和\n C语言中有很多字符 a.可显字符 b.控制字符 对于回车其实有两个动作,首先换行,在将光标指向最左侧 \r :回车 \n:换行 下面举个例子: 把\n去掉会怎样 什么都没输出。为什么? 2.缓冲区概念 观察下两个…...
CentOS7环境安装tomcat
环境准备 由于是在练习,为了方便,我们可以 1.关闭防火墙 systemctl disable firewalld.service systemctl stop firewalld.service 2.关闭selinux 在/etc/selinux/config中,设置: SELINUXdisabled 3.准备jdk---》jdk-8u333-li…...

C# 中使用ValueTask优化异步方法
概要 我们在开发过程中,经常使用async的异步方法,但是有些时候,异步的方法中,可能包含一些同步的处理。本文主要介绍通过ValueTask这个struct,优化异步处理的方法性能。 代码及实现 有些时候我们会缓存一些数据在内…...

KVM创建新的虚拟机(图形化)
1.启动kvm管理器 [rootlocalhost ~]# virt-manager2.点击创建虚拟机 3.选择所需os安装镜像 4.选择合适的内存大小和CPU 5.创建所需磁盘 6.命名创建的虚拟机...

正则表达式在格式校验中的应用以及包装类的重要性
文章目录 正则表达式:做格式校验包装类:在基本数据类型与引用数据类型间的桥梁总结 在现代IT技术岗位的面试中,掌握正则表达式的应用以及理解包装类的重要性是非常有益的。这篇博客将围绕这两个主题展开,帮助读者更好地面对面试挑…...

Docker使用之java项目工程的部署
同样本文的基础建立在已在目标服务器(以linux为示例)上安装了docker,安装教程请移步度娘 若容器存在请先停止,在删除,然后删除镜像重新编译 //停止容器 sudo docker stop datatransfer//删除容器 sudo docker rm dat…...
3ds Max如何进行合成的反射光泽通道渲染
推荐: NSDT场景编辑器 助你快速搭建可二次开发的3D应用场景 1. 准备场景 步骤 1 打开 3ds Max。smart_phone.max打开已 随教程提供。 打开 3ds Max 步骤 2 按 M 打开材质编辑器。选择空材料 槽。单击漫射通道。它将打开材质/贴图浏览器窗口。选择位图࿰…...

114、Spring AOP是如何实现的?它和AspectJ有什么区别?
Spring AOP是如何实现的?它和AspectJ有什么区别? 一、AOP的理解1、spring aop:动态代理实现2、spring aop 和 AspectJ的区别3、小图一、AOP的理解 其实,AOP只是一种编程思想,表示面向切面编程,如果想实现这种思想,可以使用动态代理啊,第三方的框架 AspectJ啊等等。 1…...

正则表达式速通
简介 正则表达式,我们可以看作通配符的增强版,可以帮我们匹配指定规则的字符串,在计算机中应用广泛,比如说爬虫、网站的登录表单等。 原视频:https://www.bilibili.com/video/BV1da4y1p7iZ 学习正则表达式的常用工具…...
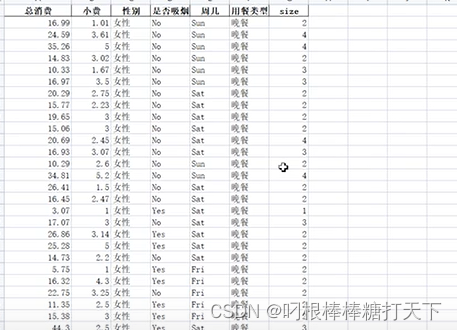
数据可视化(5)热力图及箱型图
1.热力图 #基本热力图 #imshow(x) #x,数据 x[[1,2],[3,4],[5,6],[7,8],[9,10]] plt.imshow(x) plt.show() #使用热力图分析学生的成绩 dfpd.read_excel(学生成绩表.xlsx) #:表示行号 截取数学到英语的列数 xdf.loc[:,"数学":英语].…...

React 组件通信-全面解析
父子组件通信 // 导入 import { useState } from "react";import "./App.scss"; import { defaultTodos } from "./components/module/contentData";// 子组件 const Module ({ id, done, text, onToggle, onDelData }) > {return (<div…...

“深入理解Spring Boot:快速构建微服务架构的利器“
标题:深入理解Spring Boot:快速构建微服务架构的利器 摘要:Spring Boot是一种基于Spring框架的开源项目,它通过自动化配置和约定优于配置的原则,使得开发者能够快速构建微服务架构。本文将深入介绍Spring Boot的特点和…...

SpringBoot超级详解
1.父工程的父工程 在父工程的父工程中的核心依赖,专门用来版本管理的 版本管理。 2.父工程 资源过滤问题,都帮解决了,什么配置文件,都已经配置好了,资源过滤问题是帮助,过滤解决让静态资源文件能够过滤到…...
手机的python怎么运行文件,python在手机上怎么运行
大家好,小编来为大家解答以下问题,手机上的python怎么运行程序,手机的python怎么运行文件,今天让我们一起来看看吧! 1、python程序怎么在手机上运行 python语言应用很广泛,自己也很喜欢使用它,其…...
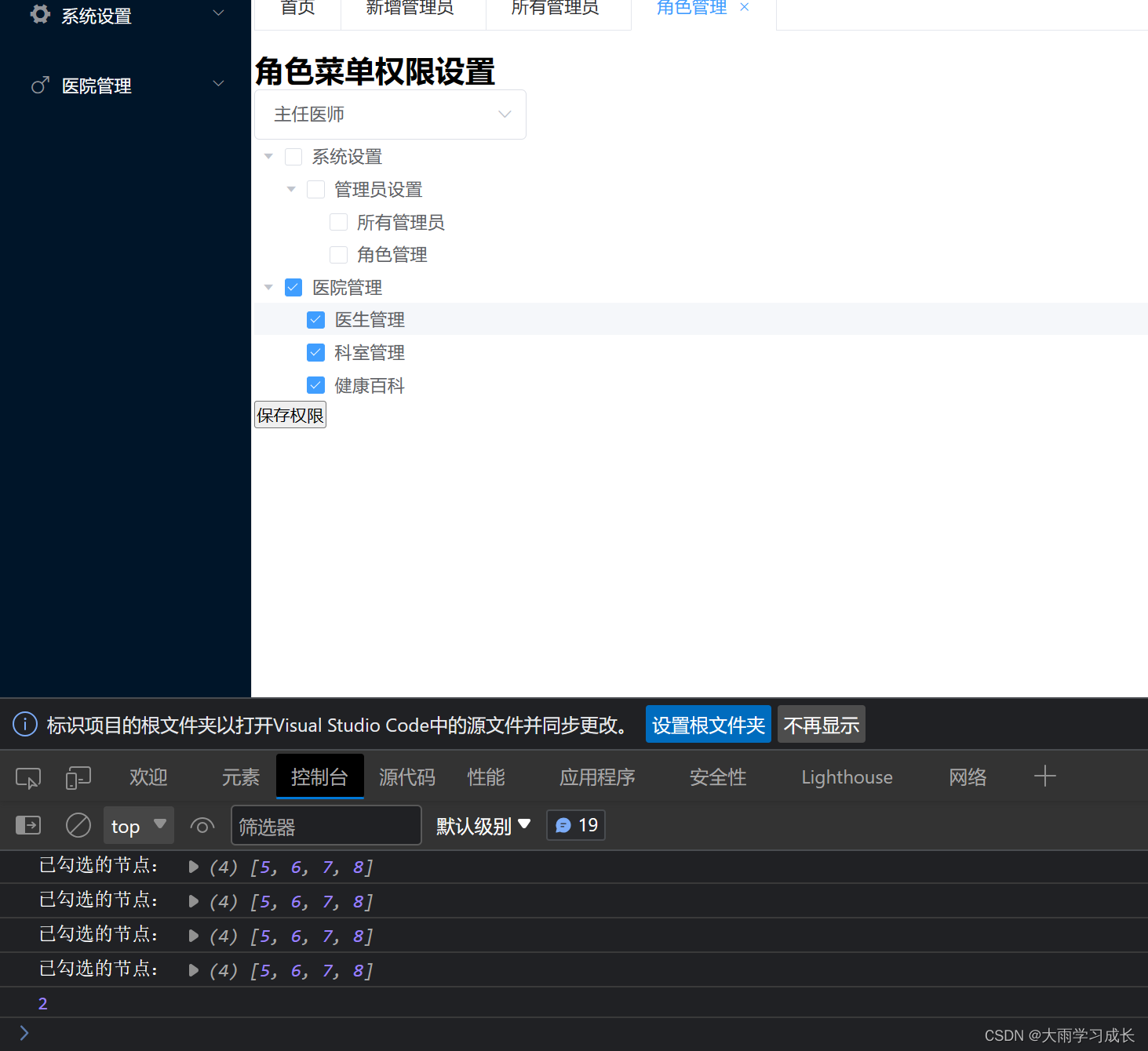
RBAC三级树状菜单实现(从前端到后端)未完待续
1、表格设计 RBAC 2、前端路由 根据不同的用户id显示不同的菜单。 根据路由 3、多级菜单 展示所有权限,并且根据当前用户id展示它所属的角色的所有菜单。 前端树状展示 思路: 后端:传给前端map,map里1个是所有菜单&am…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
