P5691 [NOI2001] 方程的解数
[NOI2001] 方程的解数
题目描述
已知一个 n n n 元高次方程:
∑ i = 1 n k i x i p i = 0 \sum\limits_{i=1}^n k_ix_i^{p_i} = 0 i=1∑nkixipi=0
其中: x 1 , x 2 , … , x n x_1, x_2, \dots ,x_n x1,x2,…,xn 是未知数, k 1 , k 2 , … , k n k_1,k_2, \dots ,k_n k1,k2,…,kn 是系数, p 1 , p 2 , … p n p_1,p_2,…p_n p1,p2,…pn 是指数。且方程中的所有数均为整数。
假设未知数 x i ∈ [ 1 , m ] ( i ∈ [ 1 , n ] ) x_i \in [1,m] \space ( i \in [1,n]) xi∈[1,m] (i∈[1,n]),求这个方程的整数解的个数。
输入格式
第一行一个正整数 n n n,表示未知数个数。
第二行一个正整数 m m m。
接下来 n n n 行,每行两个整数 k i , p i k_i,p_i ki,pi。
输出格式
输出一行一个整数,表示方程解的个数。
样例 #1
样例输入 #1
3
150
1 2
-1 2
1 2
样例输出 #1
178
提示
【数据范围】
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 6 1\le n \le 6 1≤n≤6, 1 ≤ m ≤ 150 1\le m \le 150 1≤m≤150,且
∑ i = 1 n ∣ k i m p i ∣ < 2 31 \sum\limits_{i=1}^n |k_im^{p_i}| < 2^{31} i=1∑n∣kimpi∣<231
答案不超过 2 31 − 1 2^{31}-1 231−1, p i ∈ N ∗ p_i \in \mathbb N^* pi∈N∗。
分析
数据较小,使用折半搜索,每个搜索搜一半,先枚举出每个可能性,再查找即可
代码
#include <bits/stdc++.h>
using namespace std;
const int M = 1e7;
int n, m, tot, ans;
int b[M];
int k[10], p[10];
void read() {cin >> n >> m;for (int i = 1; i <= n; i++) cin >> k[i] >> p[i];
}
int powm(int x, int b) {if (b == 0) return 1;int res = pow(x, b >> 1);if (b % 2 == 0) return res * res;return res * res * x;
}
void dfs1(int i,int sum) {if (i > n) { b[++tot] = -sum; return; }for (int x = 1; x <= m; x++) {int t = powm(x, p[i]) * k[i];dfs1(i + 1, sum + t);}
}
void dfs2(int i, int sum) {if (i > n / 2) {int res = upper_bound(b + 1, b + 1 + tot, sum) - lower_bound(b + 1, b + 1 + tot, sum);ans += res; return;}for (int x = 1; x <= m; x++) {int t = powm(x, p[i]) * k[i];dfs2(i + 1, sum + t);}
}
int main() {read();dfs1(n / 2 + 1, 0);sort(b + 1, b + 1 + tot);dfs2(1, 0);cout << ans;return 0;
}
分析
int powm(int x, int b) {if (b == 0) return 1;int res = pow(x, b >> 1);if (b % 2 == 0) return res * res;return res * res * x;
}
由于是高次方程,可以使用快速幂优化
void dfs1(int i,int sum) {if (i > n) { b[++tot] = -sum; return; }for (int x = 1; x <= m; x++) {int t = powm(x, p[i]) * k[i];dfs1(i + 1, sum + t);}
}
由于 x ∈ [ 1 , m ] x \in [1,m] x∈[1,m],所以枚举每个x的值,算出一半的答案,记录在数组中
void dfs2(int i, int sum) {if (i > n / 2) {int res = upper_bound(b + 1, b + 1 + tot, sum) - lower_bound(b + 1, b + 1 + tot, sum);ans += res; return;}for (int x = 1; x <= m; x++) {int t = powm(x, p[i]) * k[i];dfs2(i + 1, sum + t);}
}
与dfs1基本相同,但搜索完毕后记得统计答案数,更新ans即可
相关文章:

P5691 [NOI2001] 方程的解数
[NOI2001] 方程的解数 题目描述 已知一个 n n n 元高次方程: ∑ i 1 n k i x i p i 0 \sum\limits_{i1}^n k_ix_i^{p_i} 0 i1∑nkixipi0 其中: x 1 , x 2 , … , x n x_1, x_2, \dots ,x_n x1,x2,…,xn 是未知数, k 1 ,…...

rust里用什么表示字节类型?
在Rust中,字节可以使用 u8 类型来表示。 u8 是一个无符号8位整数类型,可以表示0到255之间的值,对应于一个字节的范围。 以下是一个示例,演示了如何声明和使用字节: fn main() {let byte: u8 65; // 表示字母A的ASCI…...
CMake简介
文章目录 为什么需要头文件为什么 C 需要声明头文件 - 批量插入几行代码的硬核方式头文件进阶 - 递归地使用头文件 CMake什么是编译器多文件编译与链接CMake 的命令行调用为什么需要库(library)CMake 中的静态库与动态库CMake 中的子模块子模块的头文件如…...
[threejs]相机与坐标
搞清相机和坐标的关系在threejs初期很重要,否则有可能会出现写了代码,运行时一片漆黑的现象,这种情况就有可能是因为你相机没弄对。 先来看一下threejs中的坐标(世界坐标) 坐标轴好理解,大家只需要知道在three中不同颜色代表的轴…...

Qt信号与槽机制的基石-MOC详解
引入 上篇讲到了信号与槽就是实现的观察者模式,那具体如何生成映射表就是moc做的事情。 一、moc简介 1. moc的定义 moc 全称是 Meta-Object Compiler,也就是“元对象编译器”,它主要用于处理C源文件中的非标准C代码。Qt 程序在交由标准编…...

关于单体架构缓存刷新实现方案
背景 如果各位看官是分布式项目应该都采用分布式缓存了,例如redis等,分布式缓存不在本次讨论范围哈;我个人建议是,如果是用户量比较大,建议采用分布式缓存机制,后期可以很容易前后到分布式服务或微服务。 …...

洞悉安全现状,建设网络安全防护新体系
一、“网络攻防演练行动“介绍 国家在2016年发布《网络安全法》,出台网络安全攻防演练相关规定:关键信息基础设施的运营者应“制定网络安全事件应急预案,并定期进行演练”。同年“实战化网络攻防演练行动”成为惯例。由公安部牵头࿰…...
spring中怎么通过静态工厂和动态工厂获取对象以及怎么通过 FactoryBean 获取对象
😀前言 本章是spring基于XML 配置bean系类中第4篇讲解spring中怎么通过静态工厂和动态工厂获取对象以及怎么通过 FactoryBean 获取对象 🏠个人主页:尘觉主页 🧑个人简介:大家好,我是尘觉,希望…...
)
三元组表实现矩阵相加(数据结构)
代码: 含注释,供参考 #include <stdio.h> #include <stdlib.h>typedef struct {int row,col,value;//分别为行数,列数,数值 } Triple; typedef struct {int len;//非零数值的个数Triple data[200]; } TSMatrix;void…...

ChinaJoy 2023微星雷鸟17游戏本震撼发布:搭载AMD锐龙9 7945HX首发8499元
ChinaJoy 2023展会中微星笔记本再次给大家带来惊喜,发布了搭载AMD移动端16大核的旗舰游戏本:雷鸟17,更重要的这样一款旗舰性能的游戏本,首发价8499元堪称当今游戏本市场中的“性价比爆款”! 本着和玩家一同制霸游戏战场…...

各种运算符
算术运算符 1.双目运算符 */%:从左到右优先级依次降低 一些注意事项: 1若a/b都为整型那么结果也为整型,如果ab其中有一个为实型,结果则为实型 求余运算符注意事项: 1运算对象必须为整数 2运算结果的整数跟左边数字的…...
yolov3-tiny原理解析及代码分析
前言 从去年十一月份开始学习yolo神经网络用于目标识别的硬件实现,到现在已经六个月了。一个硬件工程师,C/C基础都差劲的很,对照着darknet作者的源码和网上东拼西凑的原理讲解,一点一点地摸索。刚开始进度很慢,每天都…...

深入了解Redis-实战篇-短信登录
深入了解Redis-实战篇-短信登录 一、故事背景二、知识点主要构成2.1、短信登录2.1.1、生成随机短信验证码引入maven依赖生成验证码 2.1.2、实现登录校验拦截器2.1.3、基于Redis实现短信登录2.1.3.1、发送验证码时存入Redis2.1.3.2、登录时校验验证码 2.1.4、解决状态登录刷新的…...
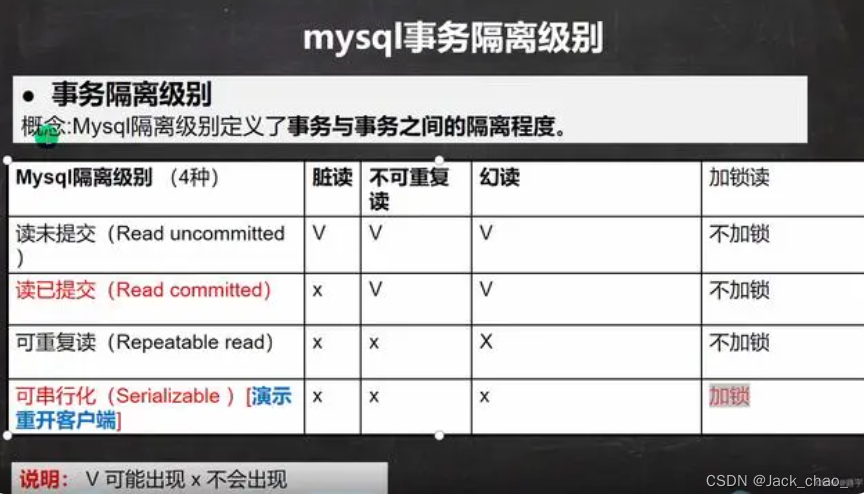
Mysql的锁
加锁的目的 对数据加锁是为了解决事务的隔离性问题,让事务之前相互不影响,每个事务进行操作的时候都必须先加上一把锁,防止其他事务同时操作数据。 事务的属性 (ACID) 原子性 一致性 隔离性 持久性 事务的隔离级别 锁…...

【EI/SCOPUS征稿】2023年算法、图像处理与机器视觉国际学术会议(AIPMV2023)
2023年算法、图像处理与机器视觉国际学术会议(AIPMV2023) 2023 International Conference on Algorithm, Image Processing and Machine Vision(AIPMV2023) 2023年算法、图像处理与机器视觉国际学术会议(AIPMV2023&am…...
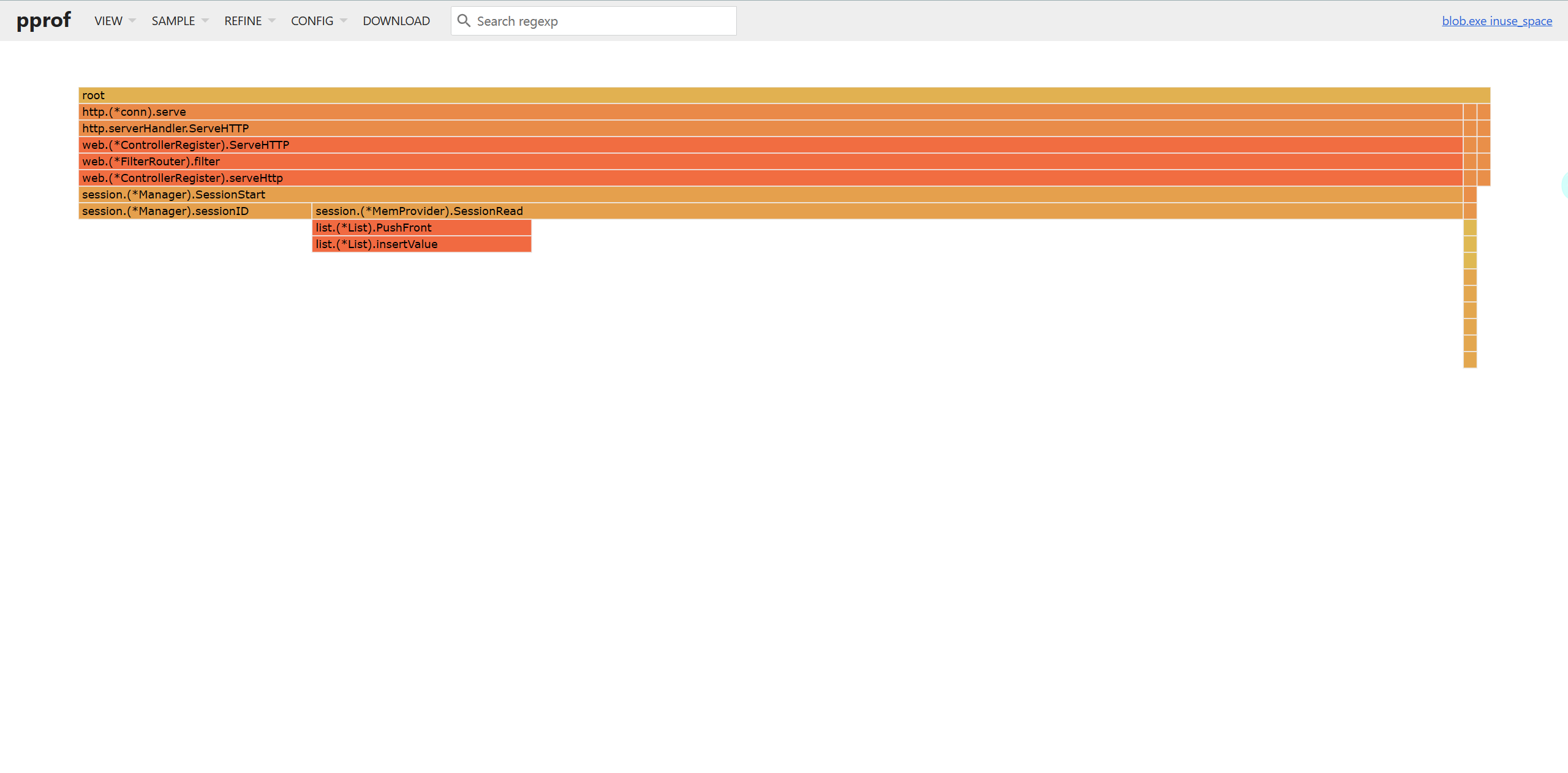
Go语言性能优化建议与pprof性能调优详解——结合博客项目实战
文章目录 性能优化建议Benchmark的使用slice优化预分配内存大内存未释放 map优化字符串处理优化结构体优化atomic包小结 pprof性能调优采集性能数据服务型应用go tool pprof命令项目调优分析修改main.go安装go-wrk命令行交互界面图形化火焰图 性能优化建议 简介: …...
)
K阶斐波那契数列(数据结构)
代码: 注意k阶斐波那契序列定义:第k和k1项为1,前k - 1项为0,从k项之后每一项都是前k项的和 例如:k2时,斐波那契序列为:0,1,1,2,3,5,8,13... k3时,斐波那契序列为:0,0,…...

【JavaEE】博客系统前后端交互
目录 一、准备工作 二、数据库的表设计 三、封装JDBC数据库操作 1、创建数据表对应的实体类 2、封装增删改查操作 四、前后端交互逻辑的实现 1、博客列表页 1.1、展示博客列表 1.2、博客详情页 1.3、登录页面 1.4、强制要求用户登录,检查用户的登录状态 …...
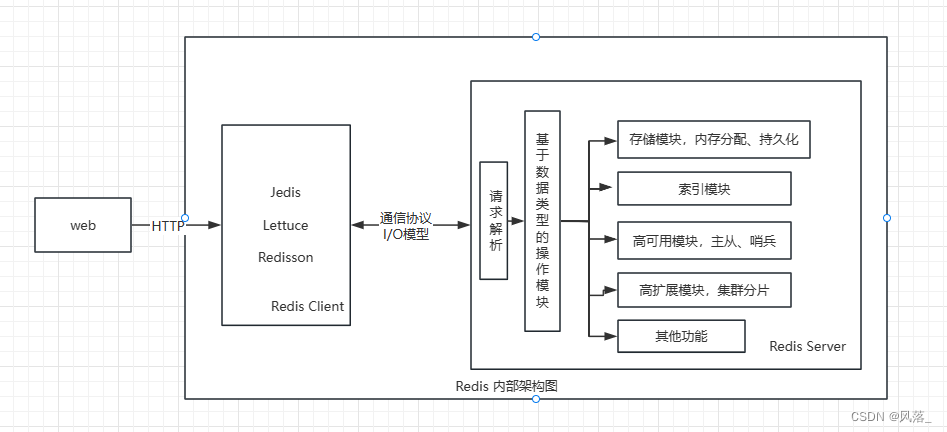
Redis 简介
文章目录 Redis 简介 Redis 简介 Redis(Remote Dictionary Server),远程词典服务器,基于 C/S 架构,是一个基于内存的键值型 NoSQL 数据库,开源,遵守 BSD 协议,Redis 由 C语言 实现。…...

CS162 13-17 虚拟内存
起源 为啥我们需要虚拟内存-----------需求是啥? 可以给程序提供一个统一的视图,比如多个程序运行同一个代码段的话,同一个kernel,就可以直接共享 cpu眼里的虚拟内存 无限内存的假象 设计迭代过程 为啥这样设计? 一…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
