2023年第四届“华数杯”数学建模思路 - 复盘:光照强度计算的优化模型
文章目录
- 0 赛题思路
- 1 问题要求
- 2 假设约定
- 3 符号约定
- 4 建立模型
- 5 模型求解
- 6 实现代码
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 问题要求
现在已知一个教室长为15米,宽为12米,在距离地面高2.5米的位置均
匀的安放4个光源(分别为1、2、3、4),各个光源的光照强度均为一个单位,如下图
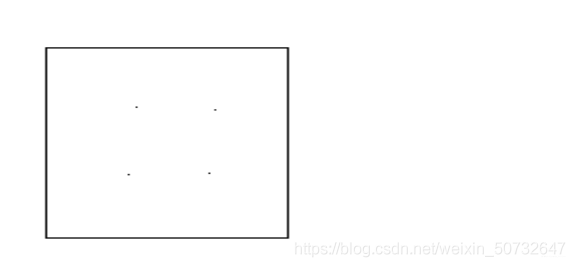
要求:
- (1)如何计算教室内任意一点的光照强度?(光源对目标点的光照强度与该光源到目标点距离的平方成反比,与该光源的强度成正比).
- (2)画出距离地面1米处各个点的光照强度与位置(横纵坐标)之间的函数关系曲面图,试同时给出一个近似的函数关系式.
- (3)假设离地面1米高正是学生桌面的高度,如何设计这四个点光源的位置,才能使学生对光照的平均满意度达到最高?
- (4)若将题目中的点光源换成线光源,以上(2)、(3)问的结果又如何?
(对于(1)、(2)问,假设横向(纵向)墙壁与光源、光源与光源、光源与墙壁之间的距离是相等的.)
2 假设约定
- 1 光不会通过窗、门等外涉,也不考虑光在空气中的消耗,即光照强度和不变;
- 2 室内不受外界光源影响;
- 3 教室高度为2.5米;
- 4 不考虑光的反射;
- 5 线光源发光是均匀的.
3 符号约定

4 建立模型
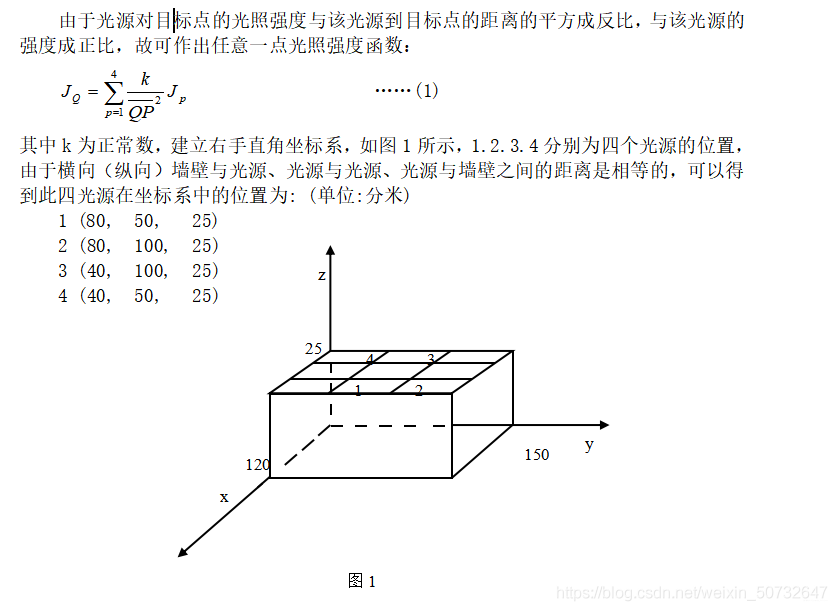

5 模型求解

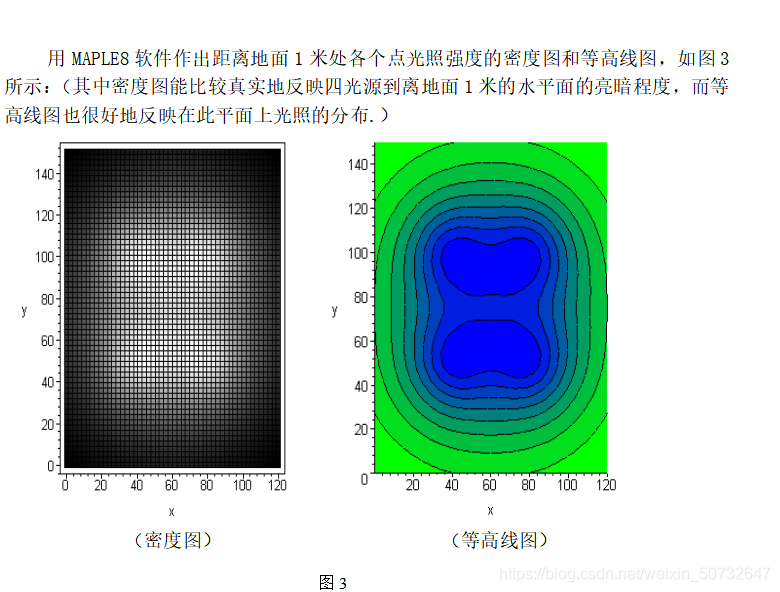
6 实现代码
matlab 实现代码
建议最好用python去实现,图会好看一些,而且国内当前趋势会逐渐淘汰matlab,目前有些学校已经无法使用matlab了
clear
clc
max=0;min=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));endendif l>maxmax=l;x11=x1;y11=y1;x12=x2;y12=y2;x13=x3;y13=y3;x14=x4;y14=y4;endp=l./(120.*150);Q=0;for x=0:0.1:12for y=0:0.1:15Q=Q+(k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2))-p).^2.^(1./2);endendif min>Qmin=Q;x21=x1;y21=y1;x22=x2;y22=y2;x23=x3;y23=y3;x24=x4;y24=y4;endend
end
disp(['最大值','x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
disp(['最平均','x21=',num2str(x21),' ','y21=',num2str(y21),' ','x22=',num2str(x22),' ','y22=',num2str(y22),' ','x23=',num2str(x23),' ','y23=',num2str(y23),' ','x24=',num2str(x24),' ','y24=',num2str(y24)])
附录二:
clear
clc
max=0;min=4;li=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;e=0for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));r=k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));e=e+(r-6*10^(-32))^2;endendS=(l-0.1278)^2+eif S<lili=Sx11=x1,y11=y1, x12=x2,y12=y2, x13=x3,y13=y3, x14=x4,y14=y4,en4en4
en4
disp(['x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
li
相关文章:

2023年第四届“华数杯”数学建模思路 - 复盘:光照强度计算的优化模型
文章目录 0 赛题思路1 问题要求2 假设约定3 符号约定4 建立模型5 模型求解6 实现代码 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 问题要求 现在已知一个教室长为15米,宽为12米࿰…...
)
Typescript第七章 处理错误(返回null,抛出异常,返回异常,Option类型)
第七章 处理错误 Typescript竭尽所能,把运行时异常转移到编译时。Typescript是功能丰富的系统,加上强大的静态和符号分析能力,包揽了大量辛苦的工作。 但是有些问题是无法避免的,比如网络和文件系统异常,解析用户输入…...

Qt库xcb问题
首先在~/.bashrc中加入 export QT_DEBUG_PLUGINS1然后看具体的报错 查看某个库链接的库: ldd libqxcb.so然后找到真正缺少的库,再在路径下搜索,然后建立软链接。 https://blog.csdn.net/LOVEmy134611/article/details/107212845 https://…...

C++ | 哈希表的实现与unordered_set/unordered_map的封装
目录 前言 一、哈希 1、哈希的概念 2、哈希函数 (1)直接定址法 (2)除留余数法 (3)平方取中法(了解) (4)随机数法(了解) 3、哈…...
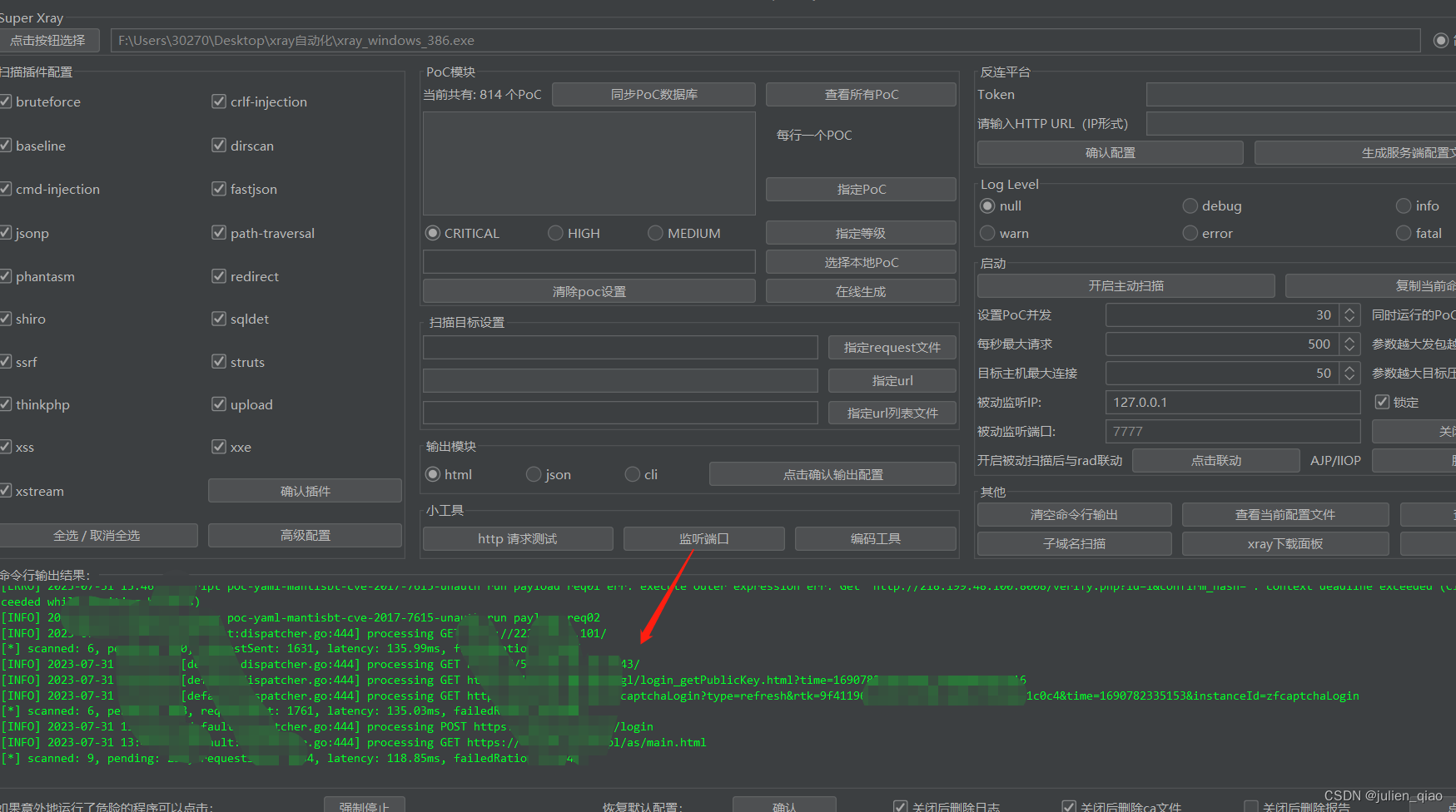
【漏洞挖掘】Xray+rad自动化批量漏洞挖掘
文章目录 前言一、挖掘方法二、使用步骤工具安装使用方法开始挖掘 总结 前言 自动化漏洞挖掘是指利用计算机程序和工具来扫描、分析和检测应用程序、网络和系统中的安全漏洞的过程。这种方法可以帮助安全专家和研究人员更高效地发现和修复潜在的安全威胁,从而提高整…...

Swagger UI教程 API 文档和Node的使用
在团队开发中,一个好的 API 文档可以减少很多交流成本,也可以使一个新人快速上手业务。 前言 swagger ui是一个API在线文档生成和测试的利器,目前发现最好用的。为什么好用?Demo 传送门 支持API自动生成同步的在线文档 这些文档可…...

P5691 [NOI2001] 方程的解数
[NOI2001] 方程的解数 题目描述 已知一个 n n n 元高次方程: ∑ i 1 n k i x i p i 0 \sum\limits_{i1}^n k_ix_i^{p_i} 0 i1∑nkixipi0 其中: x 1 , x 2 , … , x n x_1, x_2, \dots ,x_n x1,x2,…,xn 是未知数, k 1 ,…...

rust里用什么表示字节类型?
在Rust中,字节可以使用 u8 类型来表示。 u8 是一个无符号8位整数类型,可以表示0到255之间的值,对应于一个字节的范围。 以下是一个示例,演示了如何声明和使用字节: fn main() {let byte: u8 65; // 表示字母A的ASCI…...
CMake简介
文章目录 为什么需要头文件为什么 C 需要声明头文件 - 批量插入几行代码的硬核方式头文件进阶 - 递归地使用头文件 CMake什么是编译器多文件编译与链接CMake 的命令行调用为什么需要库(library)CMake 中的静态库与动态库CMake 中的子模块子模块的头文件如…...
[threejs]相机与坐标
搞清相机和坐标的关系在threejs初期很重要,否则有可能会出现写了代码,运行时一片漆黑的现象,这种情况就有可能是因为你相机没弄对。 先来看一下threejs中的坐标(世界坐标) 坐标轴好理解,大家只需要知道在three中不同颜色代表的轴…...

Qt信号与槽机制的基石-MOC详解
引入 上篇讲到了信号与槽就是实现的观察者模式,那具体如何生成映射表就是moc做的事情。 一、moc简介 1. moc的定义 moc 全称是 Meta-Object Compiler,也就是“元对象编译器”,它主要用于处理C源文件中的非标准C代码。Qt 程序在交由标准编…...

关于单体架构缓存刷新实现方案
背景 如果各位看官是分布式项目应该都采用分布式缓存了,例如redis等,分布式缓存不在本次讨论范围哈;我个人建议是,如果是用户量比较大,建议采用分布式缓存机制,后期可以很容易前后到分布式服务或微服务。 …...

洞悉安全现状,建设网络安全防护新体系
一、“网络攻防演练行动“介绍 国家在2016年发布《网络安全法》,出台网络安全攻防演练相关规定:关键信息基础设施的运营者应“制定网络安全事件应急预案,并定期进行演练”。同年“实战化网络攻防演练行动”成为惯例。由公安部牵头࿰…...
spring中怎么通过静态工厂和动态工厂获取对象以及怎么通过 FactoryBean 获取对象
😀前言 本章是spring基于XML 配置bean系类中第4篇讲解spring中怎么通过静态工厂和动态工厂获取对象以及怎么通过 FactoryBean 获取对象 🏠个人主页:尘觉主页 🧑个人简介:大家好,我是尘觉,希望…...
)
三元组表实现矩阵相加(数据结构)
代码: 含注释,供参考 #include <stdio.h> #include <stdlib.h>typedef struct {int row,col,value;//分别为行数,列数,数值 } Triple; typedef struct {int len;//非零数值的个数Triple data[200]; } TSMatrix;void…...

ChinaJoy 2023微星雷鸟17游戏本震撼发布:搭载AMD锐龙9 7945HX首发8499元
ChinaJoy 2023展会中微星笔记本再次给大家带来惊喜,发布了搭载AMD移动端16大核的旗舰游戏本:雷鸟17,更重要的这样一款旗舰性能的游戏本,首发价8499元堪称当今游戏本市场中的“性价比爆款”! 本着和玩家一同制霸游戏战场…...

各种运算符
算术运算符 1.双目运算符 */%:从左到右优先级依次降低 一些注意事项: 1若a/b都为整型那么结果也为整型,如果ab其中有一个为实型,结果则为实型 求余运算符注意事项: 1运算对象必须为整数 2运算结果的整数跟左边数字的…...
yolov3-tiny原理解析及代码分析
前言 从去年十一月份开始学习yolo神经网络用于目标识别的硬件实现,到现在已经六个月了。一个硬件工程师,C/C基础都差劲的很,对照着darknet作者的源码和网上东拼西凑的原理讲解,一点一点地摸索。刚开始进度很慢,每天都…...

深入了解Redis-实战篇-短信登录
深入了解Redis-实战篇-短信登录 一、故事背景二、知识点主要构成2.1、短信登录2.1.1、生成随机短信验证码引入maven依赖生成验证码 2.1.2、实现登录校验拦截器2.1.3、基于Redis实现短信登录2.1.3.1、发送验证码时存入Redis2.1.3.2、登录时校验验证码 2.1.4、解决状态登录刷新的…...
Mysql的锁
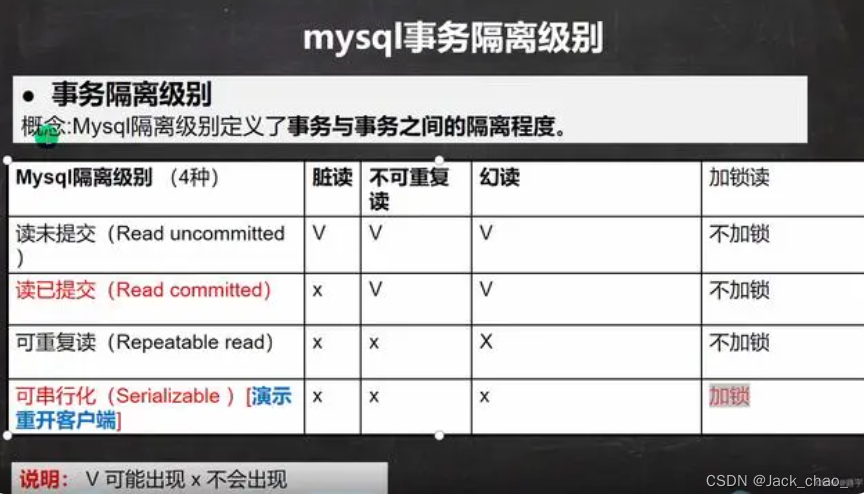
加锁的目的 对数据加锁是为了解决事务的隔离性问题,让事务之前相互不影响,每个事务进行操作的时候都必须先加上一把锁,防止其他事务同时操作数据。 事务的属性 (ACID) 原子性 一致性 隔离性 持久性 事务的隔离级别 锁…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
