3,堆,桶排序,排序总结【p4-p5】
桶排序,排序总结
- 3.1堆
- 3.1.1堆结构
- 3.1.1.1完全二叉树
- 3.1.1.2堆分为大根堆和小根堆
- 3.1.1.2.1案例1-去掉最大数字,使剩下的数字依然是大根堆
- 3.1.1.2.2案例2
- 3.1.1.2.3案例3
- 3.1.1.2.4案例4-方便制造大根堆方法
- 3.1.2堆排序
- 3.1.2.1案例-堆排序的扩展
- 3.1.2.1.1扩容
- 3.1.2.1.2※使用系统提供的堆结构
- 3.2比较器的使用
- 3.3不基于比较的排序
- 3.3.1基数排序
- 3.3.1.1基数排序 例1:
- 3.3.1.2代码原理例2:
- 3.4排序总结
- 3.4.1排序算法的稳定性
- 3.4.1.1选择排序的稳定性
- 3.4.1.2冒泡排序的稳定性
- 3.4.1.3插入排序的稳定性
- 3.4.1.4快排的稳定性
- 3.4.1.5堆排的稳定性
- 3.4.1.6计数排序与基数排序的稳定性
- 3.4.2总结
- 3.4.3工程上对排序的改进
3.1堆
堆在逻辑概念上是完全二叉树结构,堆分为大根堆和小根堆
3.1.1堆结构
堆结构就是用数组实现的完全二叉树
完全二叉树中如果每颗子树的最大值都在顶部就是大根堆
完全二叉树中如果每颗子树的最小值都在顶部就是小根堆
堆结构的heapInsert与heapify操作
堆结构的增大和减小
优先级队列结构,就是堆结构
3.1.1.1完全二叉树
完全二叉树是满二叉树或者从左往右依次变来的树
完全二叉树有1个节点,高度为1
完全二叉树有2,3个节点,高度为2
完全二叉树有4,5,6,7个节点,高度为3
完全二叉树有n个节点,高度为logn,O(logN)
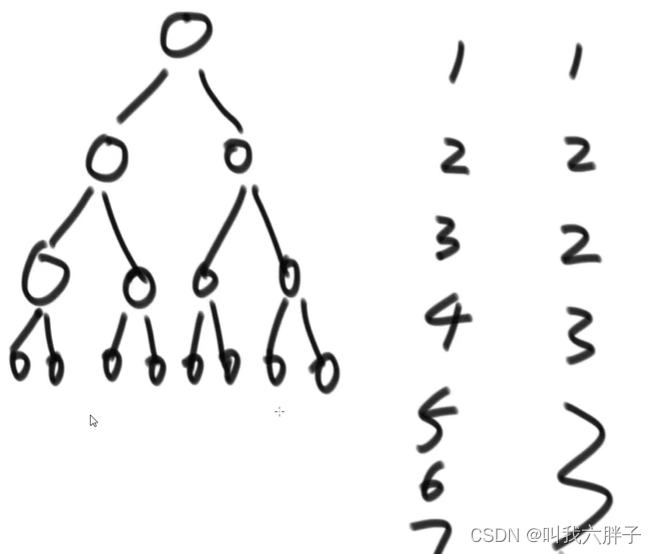
满二叉树:一个点是满二叉树,一个点下有两个点是满二叉树,一个点下两个点的下一个或各有两个点也叫满二叉树
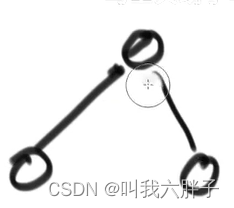
左往右依次变来的树:

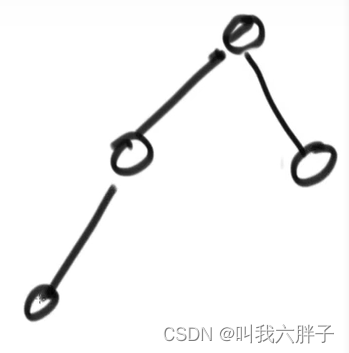
但是下图不是左往右依次变来的树
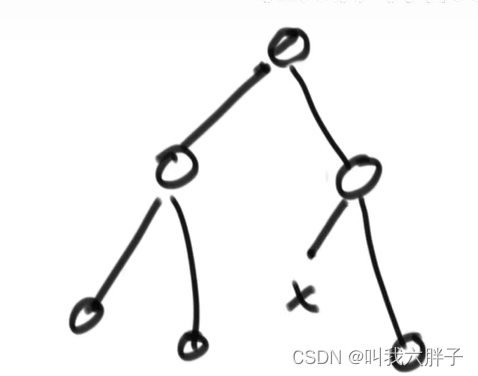
由值构成的完全二叉树
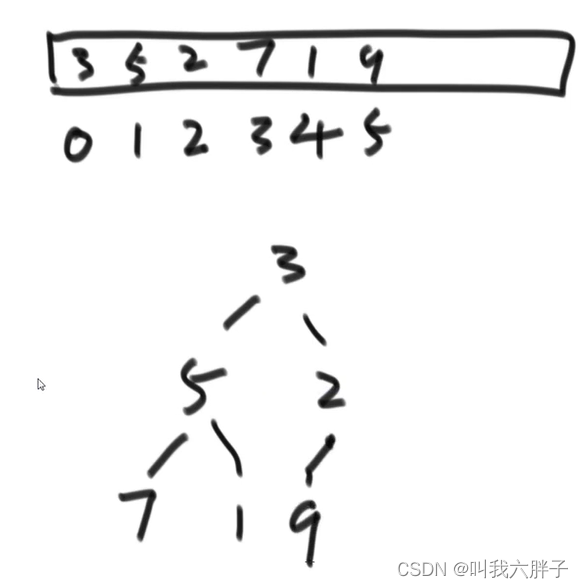
由下标构成
size=7
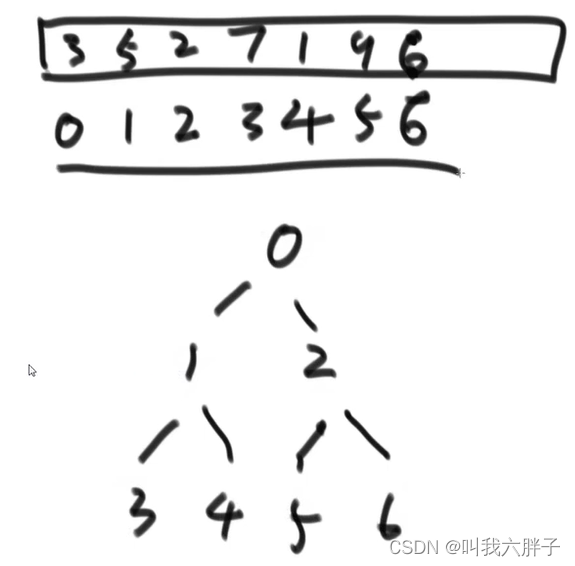
i位置的左孩子为2* i+1
i位置的右孩子为2* i+2
i位置的父为(i-1)/2
在知道size的情况下通过上方就可以找到了
3.1.1.2堆分为大根堆和小根堆
大根堆:每一个节点为头的子树,子树上最大值为头节点
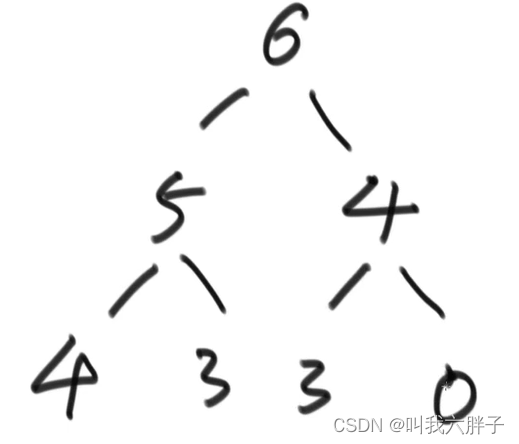
以6为头的树最大值是6,以5为头的树最大值是5……这个二叉树为大根堆
小根堆,每一个节点为头的子树,子树上最小值为头节点
怎么把数组连续触发的一段搞成一个堆?
创建一个空的数组
heapsize=0代表数组中从0出发的连续的0个数是堆
导入5,放在0位置上,heapsize=1,现在是大根堆
导入3,放在heapsize=1位置上,heapsize=2,现在是大根堆
导入6,放在heapsize=2位置上,heapsize=3,不是大根堆,需要调整,用上述公式找到父,和父5比较,比父大则交换,现在是大根堆
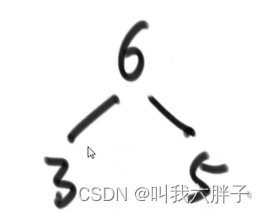
导入7,放在heapsize=3位置上,heapsize=4,不是大根堆,需要调整,用上述公式找到父,和父3比较,比父大则交换,用上述公式找到父,和父6比较,比父大则交换
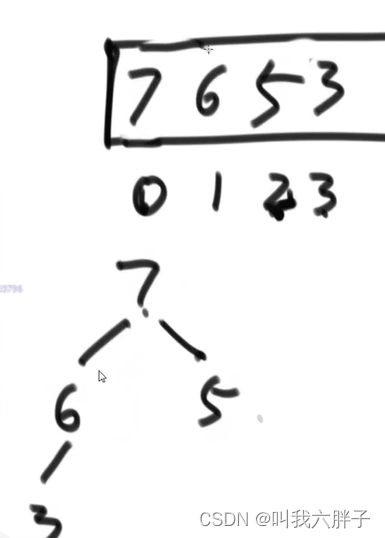
导入7,放在heapsize=4位置上,heapsize=5,不是大根堆,需要调整,用上述公式找到父,和父6比较,比父大则交换,用上述公式找到父,和父7比较,等于,是大根堆
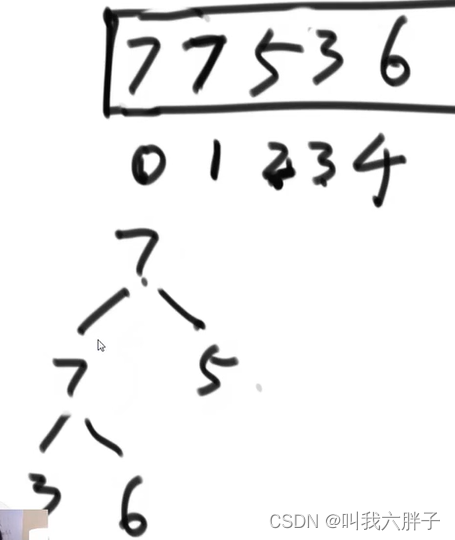
如此可保证树必定是大根堆,叫heapinsert过程
找出刚才输入的最大数字,在0位置
3.1.1.2.1案例1-去掉最大数字,使剩下的数字依然是大根堆
去掉最大数字,使剩下的数字依然是大根堆怎么做?
把已经形成的堆结构的最后一个数字放在0位置上,把heapsize减小1
用头节点看两个孩子的最大值,选最大值替换,循环此操作,知道两孩子没有比父值大的或者没有孩子时停止
#include<iostream>
#include<algorithm>
void heapify(int arr[], int index, int heapSize)
{int left = index * 2 + 1;//左孩子的下标int largest;while (left < heapSize)//左孩子是否越界(左孩子下标比右孩子下标小,可以判断有没有孩子){int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;//两个孩子中,谁的值大,把下标给largest//如果有右孩子,同时右孩子值大于左孩子的值,largest就是右孩子下标//父和孩子之间,谁的值大,把下标给largestlargest = arr[largest] > arr[index] ? largest: index;if (largest == index)//父大则退出循环{break;}std::swap(arr[largest], arr[index]);index = largest;left = index * 2 + 1;}}int main()
{int arr[9] = { 5, 3, 6, 8, 2, 4, 7, 9, 1 };for (int i = 9 / 2 - 1; i >= 0; i--) { // 从最后一个非叶子节点开始向前构建大根堆heapify(arr, i, 9);}for (int i = 0; i < 9; i++) {std::cout << arr[i] << " ";}std::cout << std::endl;std::system("pause");return 0;
}
3.1.1.2.2案例2
创建一个堆,有效区域是0到heapsize-1,i位置数变为?,怎么在i改变为?后依然让这片有效区域为大根堆
分析:
i变大,往上调整
i变小,往下调整
时间复杂度:O(logN)
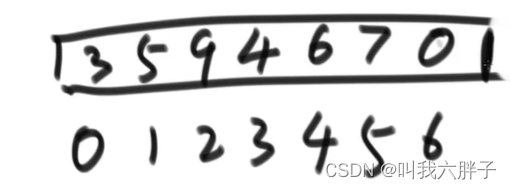
3.1.1.2.3案例3
删掉最大值,并让剩下的数重新调整成堆,时间复杂度是多少?
先让数组整体变为大根堆
heapsize=0
让0位置到0位置变为大根堆,heapsize=1
让0到1范围变为大根堆,5和3交换,heapsize=2
让0到2范围变为大根堆,9和5交换,heapsize=3
让0到3范围变为大根堆,不动,heapsize=4
让0到4范围变为大根堆,6和4交换,heapsize=5
让0到5范围变为大根堆,7和5交换,heapsize=6
让0到6范围变为大根堆,不动,heapsize=7
9673450
0位置和6位置交换变为0673459,heapsize=6(把最后的位置和堆断掉联系)怎么让其依旧为大根堆
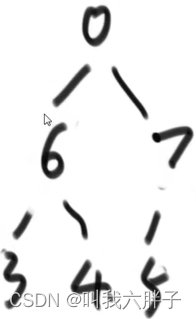
0选一个较大的孩子,和7交换
7603459
0和5交换
7653409(为什么9没动,因为heapsize=6)
继续让0和7交换,heapsize=5(7被隐藏),怎么让其依旧为大根堆
0选一个较大的孩子,和6交换
6053479
0选一个较大的孩子,和4交换
6453079
继续让0和6交换,heapsize=4(6被隐藏),怎么让其依旧为大根堆
0选一个较大的孩子,和5交换
5403679
继续让0和5交换,heapsize=3(3被隐藏),怎么让其依旧为大根堆
0选一个较大的孩子,和5交换
5403679
让0和4交换,heapsize=2(5被隐藏),为大根堆
heapsize=1
0453679
这段代码,未完成
#include<iostream>
#include<algorithm>void heapInsert(int arr[], int index);
void heapify(int arr[], int index, int heapSize);void heapSort(int arr[], int size)
{if (arr == NULL || size < 2){return;}for (int i = 0; i < size; i++)//O(N){heapInsert(arr, i);//O(logN)}int heapSize = size;std::swap(arr[0], arr[--heapSize]);while (heapSize > 0)//O(N){heapify(arr, 0, heapSize);//O(logN)std::swap(arr[0], arr[--heapSize]);//O(1)}
}void heapInsert(int arr[], int index)
{while (arr[index] > arr[(index - 1) / 2]){std::swap(arr[index], arr[(index - 1) / 2]);index = (index - 1) / 2;}
}void heapify(int arr[], int index, int heapSize)
{int left = index * 2 + 1;//左孩子的下标int largest;while (left < heapSize)//左孩子是否越界(左孩子下标比右孩子下标小,可以判断有没有孩子){largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;//两个孩子中,谁的值大,把下标给largest//如果有右孩子,同时右孩子值大于左孩子的值,largest就是右孩子下标//父和孩子之间,谁的值大,把下标给largestlargest = arr[largest] < arr[index] ? largest : index;if (largest == index)//父大则退出循环{break;}std::swap(arr[largest], arr[index]);index = largest;left = index * 2 + 1;}}int main()
{int arr[] = { 5, 3, 6, 8, 2, 4, 7, 9, 1 };int size = sizeof(arr) / sizeof(arr[0]);heapSort(arr, size);for (int i = 0; i < size; i++){std::cout << arr[i] << " ";}std::cout << std::endl;return 0;
}3.1.1.2.4案例4-方便制造大根堆方法
直接放入全部节点而不是一个一个插入时
可以从最后一个孩子的父出发,做大根堆
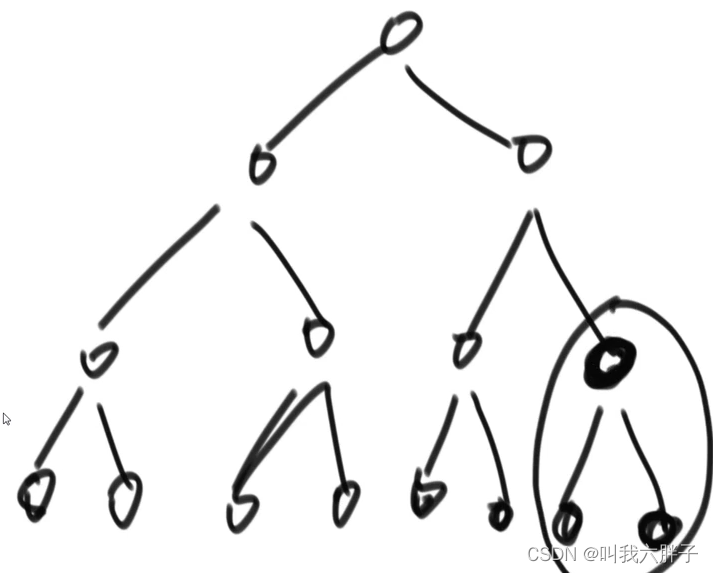
依次从最下端的父出发,做大根堆
最后一层树做完,从倒数第二层树的父出发,做大根堆
时间复杂度:
数组中有N个数,最底层节点(也叫叶节点)有多少个,N/2个
倒数第二层节点N/4个
倒数第三层节点N/8个
所以时间复杂度:
T(N)=N/2+2N/4+3N/8+4N/16+5N/32……
2T(N)=N/2+2N/2+3N/4+4N/8+5N/16……
T(N)=N/2+N/4+N/8+N/+5*N/32……
#include<iostream>
#include<algorithm>void heapInsert(int arr[], int index);
void heapify(int arr[], int index, int heapSize);void heapSort(int arr[], int size)
{if (arr == NULL || size < 2){return;}/* for (int i = 0; i < size; i++)//让整个数组变成大根堆的话用此方法{heapInsert(arr, i);}*/for (int i = size - 1; i >= 0; i--)//修改的代码,相比上述注释代码,快了一点{heapify(arr, i, size);}int heapSize = size;std::swap(arr[0], arr[--heapSize]);while (heapSize > 0)//O(N){heapify(arr, 0, heapSize);//O(logN)std::swap(arr[0], arr[--heapSize]);//O(1)}
}void heapInsert(int arr[], int index)
{while (arr[index] < arr[(index - 1) / 2]){std::swap(arr[index], arr[(index - 1) / 2]);index = (index - 1) / 2;}
}void heapify(int arr[], int index, int heapSize)
{int left = index * 2 + 1;//左孩子的下标int smallest;while (left < heapSize)//左孩子是否越界(左孩子下标比右孩子下标小,可以判断有没有孩子){smallest = left + 1 < heapSize && arr[left + 1] < arr[left] ? left + 1 : left;//两个孩子中,谁的值大,把下标给largest//如果有右孩子,同时右孩子值大于左孩子的值,largest就是右孩子下标//父和孩子之间,谁的值大,把下标给largestsmallest = arr[smallest] < arr[index] ? smallest : index;if (smallest == index)//父大则退出循环{break;}std::swap(arr[smallest], arr[index]);index = smallest;left = index * 2 + 1;}}int main()
{int arr[] = { 5, 3, 6, 8, 2, 4, 7, 9, 1 };int size = sizeof(arr) / sizeof(arr[0]);heapSort(arr, size);for (int i = 0; i < size; i++){std::cout << arr[i] << " ";}std::cout << std::endl;return 0;
}3.1.2堆排序
3.1.2.1案例-堆排序的扩展
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不超过k,并且k相对与数组来说比较小。
请选择一个合适的排序算法针对这个数据进行排序
设k=6,准备一个小根堆,
遍历前七个数
0123456,放到小根堆内,小根堆的最小值放在0位置,
7放到小根堆内,小根堆的最小值放在1位置
8放到小根堆内,小根堆的最小值放在2位置
…………
数组临近结束时,小根堆依次弹出最小值,放到数组
所以时间复杂度O(N*logk)
3.1.2.1.1扩容
一直添加变量的话需要 扩容,100变200,200变400,单词扩容的时间复杂度O(N)
假设加了N个数,扩容的次数为logN次,每一次扩容为O(N)水平,整体代价为O(NlogN),单位平均扩容代价O(NlogN)/N=O(logN)
3.1.2.1.2※使用系统提供的堆结构
需注意:系统提供的堆结构类似于黑盒,只用程序员给它一个数add,黑盒传出一个数poll
不支持,更改一个堆结构内的数,使其重新用低代价再次变为堆结构,他会扫描所有才能操作,而手写的是支持的(※有需求时候用手写堆,没需求用自带堆更方便)
3.2比较器的使用
比较器的实质就是重载比较运算符
比较器可以很好的应用在特殊标准的排序上
比较器可以很好的应用在根据特殊标准的结构上
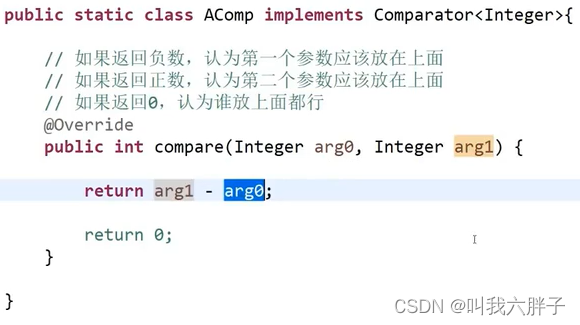
如果返回负数,认为第一个参数应该放在上面
如果返回正数,认为第二个参数应该放在前面
如果返回0,认为谁放前面都行
在类中三个元素,工号,姓名,年龄,排大小时,由大到小排序,需要自行设定用哪个元素排序,本质是c++中的重载比较运算符
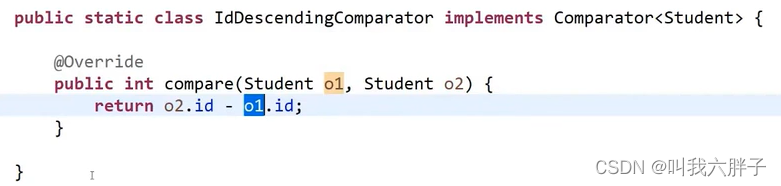

怎么做出大根堆的比较器:第二个参数减第一个参数即可
3.3不基于比较的排序
例:一个数组内均为员工年龄,0~200
建立一个201的数组,0位置代表0岁的员工多少个
1位置代表1岁的员工多少个
2位置代表2岁的员工多少个
3位置代表3岁的员工多少个
…………
遍历老数组
发现0岁的时候新数组0位置++
发现1岁的时候新数组1位置++
…………
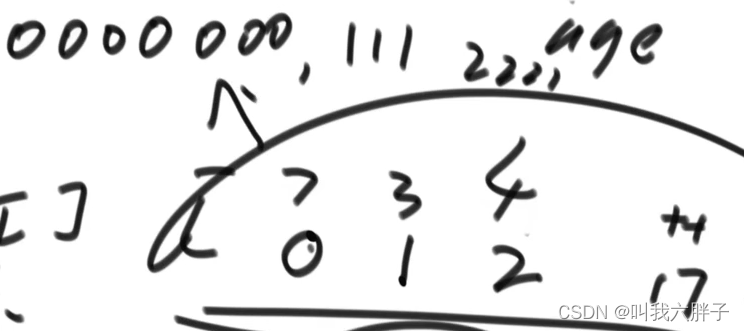
时间复杂度:O(N)
如果老数组位-2999~2999则需要创建的新数组太多了,太麻烦
所以不基于比较的排序 是根据数据状况做的排序,没有基于比较排序的应用范围广
3.3.1基数排序
3.3.1.1基数排序 例1:
本例目的:从小到大排序
[17,13,25,100,72]
先看最大数字几位:3位
所以都补成3位
[017,013,025,100,072]
准备是个容器(也可称为桶)
(桶的结构可以是数组、队列、栈、都可以)
本题中桶的结构是队列
准备0到9号桶
根据个位数放在对应桶中
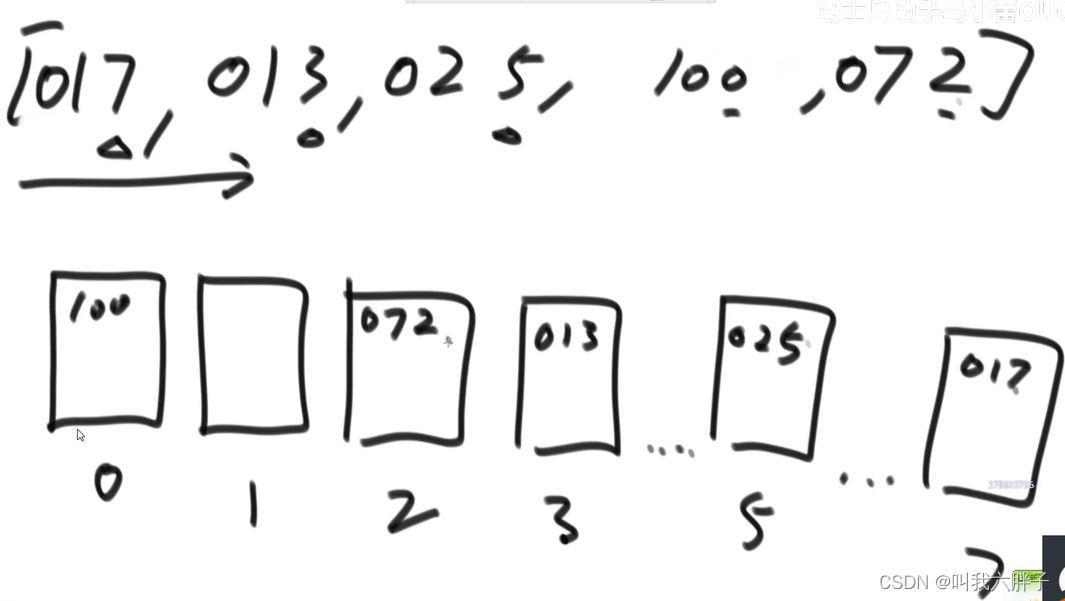
把桶中的数字依次倒出来,先进先出
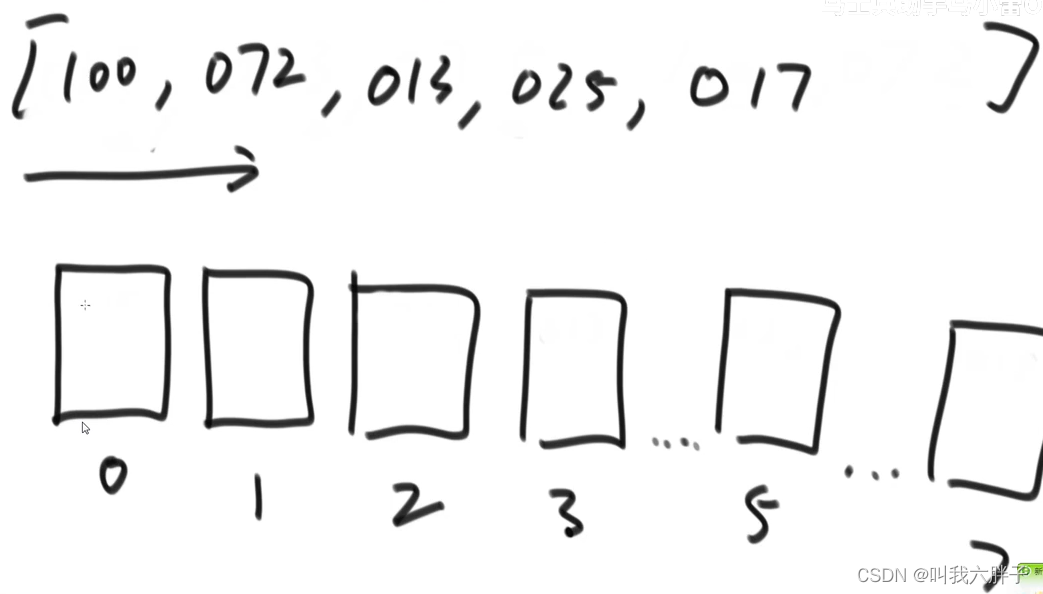
根据十位数放在对应桶中
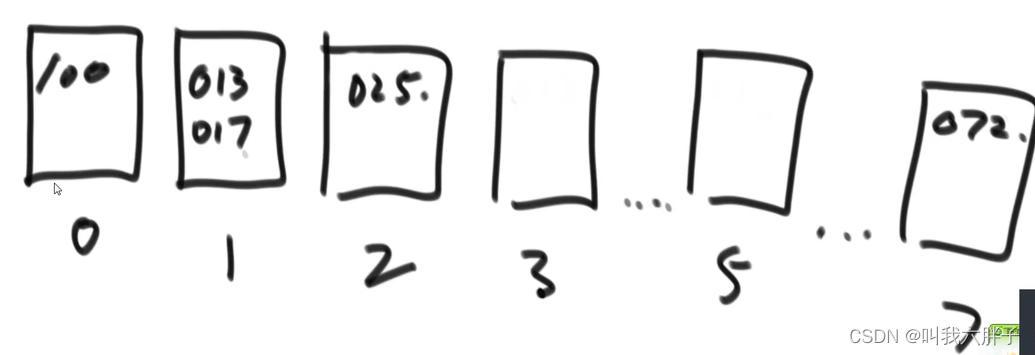
把桶中的数字依次倒出来
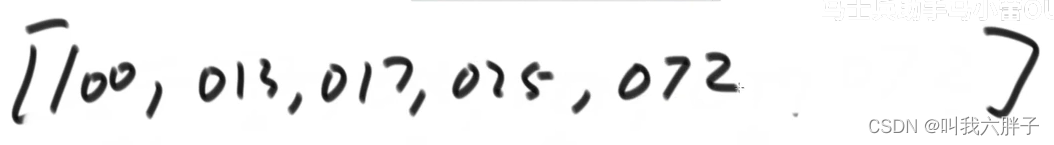
根据百位数放在对应桶中
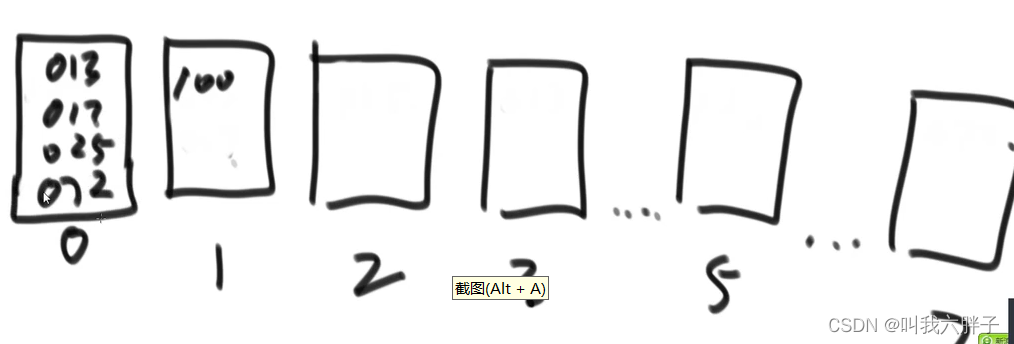
把桶中的数字依次倒出来

依然根数据状况有关,因为次排序和进制有关
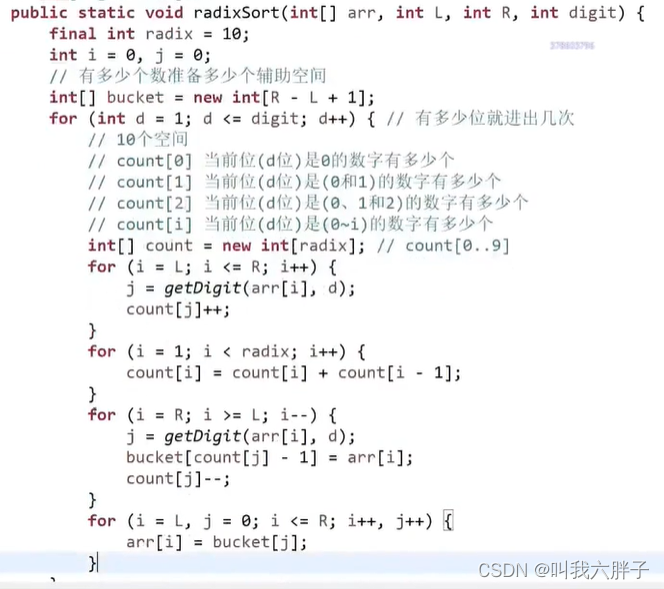
3.3.1.2代码原理例2:
[013,021,011,052,062]
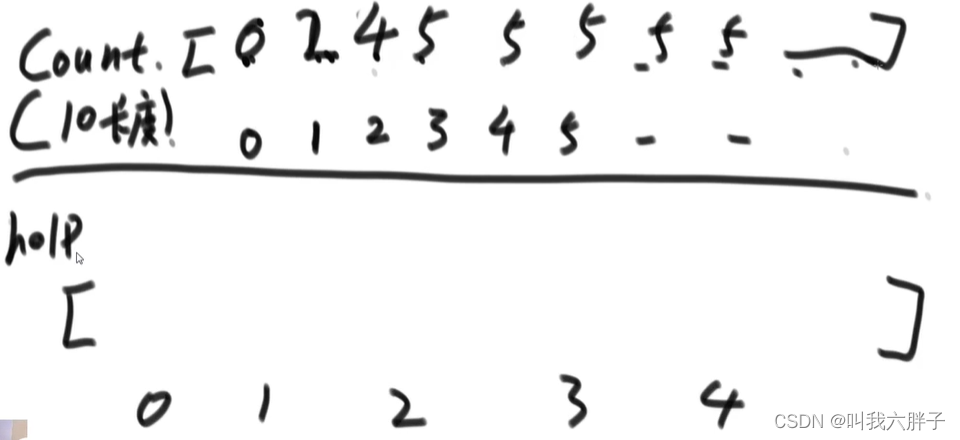
count代表个位比下标个数小与等于的个数,所以下标1有2个,下标2有2+2=4个,下标3有1+4=5个……
从右往左遍历数组(为什么从右往左遍历,因为这样等同于先出桶)
062,在下标2处,2对应的为4,所以写入新数组4-1=3位置,2位置count变为3
052,在下标2处,2对应的为3,所以写入新数组3-1=2位置,2位置count变为2
011,在下标1处,1对应的为2,所以写入新数组2-1=1位置,1位置count变为1
021,在下标1处,1对应的为1,所以写入新数组1-1=0位置,1位置count变为0
013,在下标3处,3对应的为5,所以写入新数组5-1=4位置,3位置count变为4
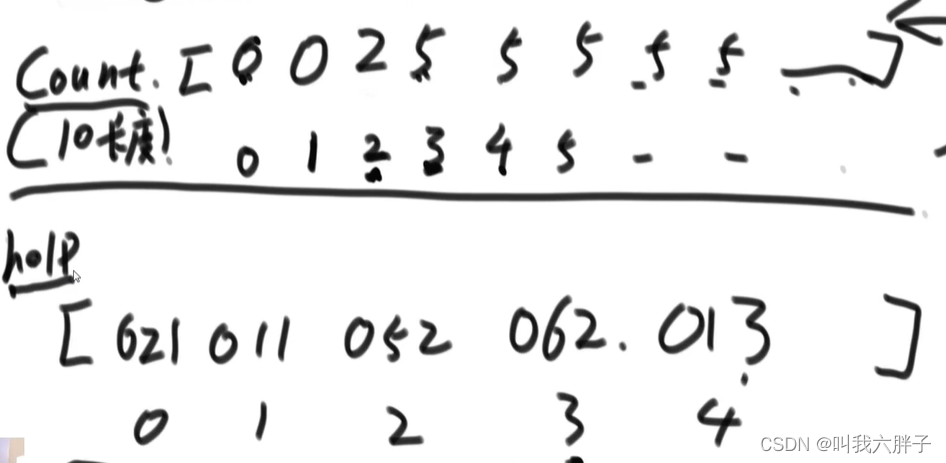
3.4排序总结
3.4.1排序算法的稳定性
同样的个体之间,如果不因为排序而改变相对次序,就是这个排序是具有稳定性的;否则就没有
不具备稳定性的排序:
选择排序、快速排序、堆排序
具备稳定性的排序:
冒泡排序、插入排序、归并排序、一切桶排序思想下的排序
目前没有找到时间复杂度O(N*logN),额外空间复杂度O(1),又稳定的排序
稳定性:值相同的元素排序之后能否保证原来的相对次序不变
[2,1,2,1,3,2,3,2]
[1,1,2,2,2,2,3,3]
原数组的第一个1和第二个1位置,在新数组中的顺序是不是还是同样的前后关系
稳定性的好处:
数个班级学生按年龄从小到大排序
再次按班级排序,如果是算法稳定的,则再每个班级的桶中,年龄依旧从小到大
在实际使用中有很多好处,比如商品先价钱排序,再好评率排序,即可得出物美价廉的商品
3.4.1.1选择排序的稳定性
不具备稳定性
[3,3,3,3,1,3,3,3,3,3,3,3]
1和第一个3做交换,所以第一个3和其他3的次序发生了改变
3.4.1.2冒泡排序的稳定性
具备稳定性
[6,5,4,5,3,4,6]
0,1,2,3,4,5,6
第一个6一直交换到下标为5处,同等大小时不交换,和同种元素第二个6位次不变,继续也是如此,所以稳定
因为同等大小时不交换所以具有稳定性,也可以同等大小时交换,这是就不具备稳定性了,所以说可以实现稳定性
3.4.1.3插入排序的稳定性
具备稳定性
[3,2,2-------]
0~0有序,3
0~1有序,第一个2和3排序,交换,第一个2和第二个2位次不变
0~2有序,第二个2和3排序,交换,第一个2和第二个2位次不变
因此具备稳定性
3.4.1.4快排的稳定性
不具备稳定性
1.0
不具备稳定性
[6,7,6,6,3]
以5作为划分值
6,7,6,6都大于5
5和3对比,5大,则3和0位置的6交换
第一个6和第二三个6的次序打乱
则不具备稳定性
2.0
不具备稳定性
[5,5,5,3,6,7]
以5作为划分值
0,1,2下标位置都为5相同,不动
5和3比较,3和0下标的数5交换,则第一个5和其他同样元素5次序打乱
则不具备稳定性
3.4.1.5堆排的稳定性
不具备稳定性
[5,4,4,6]
形成大根堆时6需要与第一个4交换,则第一个4和其他同样元素4次序打乱
则不具备稳定性
3.4.1.6计数排序与基数排序的稳定性
具备稳定性
3.4.2总结
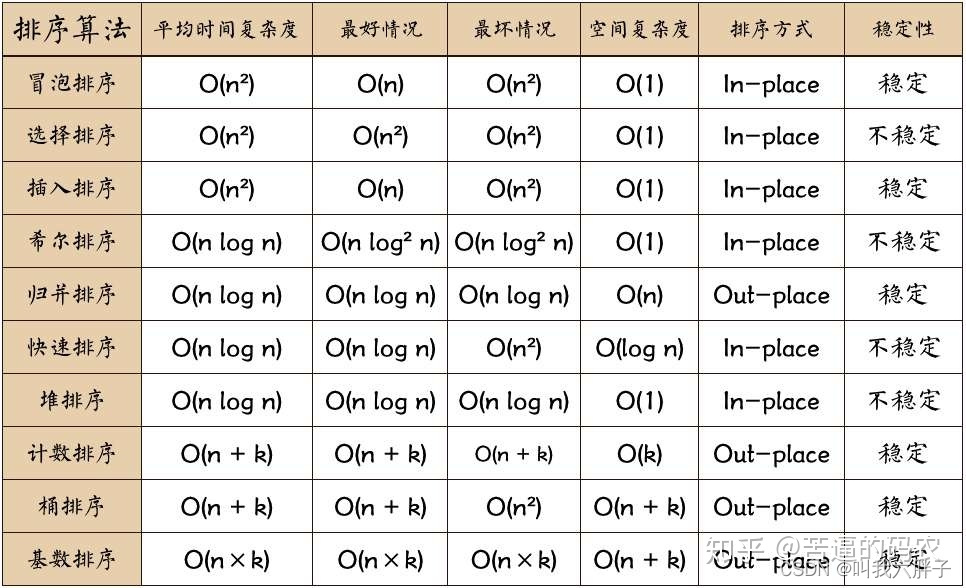
一般用的都是快排,对空间复杂度有要求时使用堆排,需要稳定性时使用堆排
问题:
基于比较的排序时间复杂度能否做到O(NlogN)以下?
目前没有,不行
时间复杂度O(NlogN)时,空间复杂度做到O(N)以下,还能做到稳定性?
目前没有,不行
常见的坑:
1,归并排序的额外空间复杂度可以变成O(1),可以,但是非常难,不需要掌握,有兴趣可以搜“归并排序内部缓存法”,变完O(1)会丧失稳定性
2,“原地归并排序”的帖子都是垃圾,会让归并排序的时间复杂度变成0(N2)
3,快速排序可以做到稳定性问题,但是非常难,不需要掌握, 可以搜“01stable sort”,达到时会使空间复杂度变为O(N)
4,所有的改进都不重要,因为目前没有找到时间复杂度0(N*logN),额外空间复杂度0(1),又稳定的排序。
5,有一道题目,是奇数放在数组左边,偶数放在数组右边,还要求原始的相对次序不变,碰到这个问题,可以怼面试官
经典快排的partion做不到稳定性,又是01标准
奇偶问题和快排01标准是一种策略,让面试官叫你这道论文级的题
3.4.3工程上对排序的改进
充分利用O(N*logN)和O(N2)排序各自的优势
稳定性的考虑
相关文章:

3,堆,桶排序,排序总结【p4-p5】
桶排序,排序总结 3.1堆3.1.1堆结构3.1.1.1完全二叉树3.1.1.2堆分为大根堆和小根堆3.1.1.2.1案例1-去掉最大数字,使剩下的数字依然是大根堆3.1.1.2.2案例23.1.1.2.3案例33.1.1.2.4案例4-方便制造大根堆方法 3.1.2堆排序3.1.2.1案例-堆排序的扩展3.1.2.1.1…...

使用langchain与你自己的数据对话(四):问答(question answering)
之前我已经完成了使用langchain与你自己的数据对话的前三篇博客,还没有阅读这三篇博客的朋友可以先阅读一下: 使用langchain与你自己的数据对话(一):文档加载与切割使用langchain与你自己的数据对话(二):向量存储与嵌入使用langc…...

如何快速开拓海外华人市场?附解决方案!
开拓华人市场对于企业来说是非常必要的。华人市场庞大且潜力巨大,拥有巨额的消费能力。随着华人经济的不断增长,越来越多的企业开始意识到华人市场的重要性。 通过开拓华人市场,企业可以获得更多的销售机会,并且在竞争激烈的市场…...
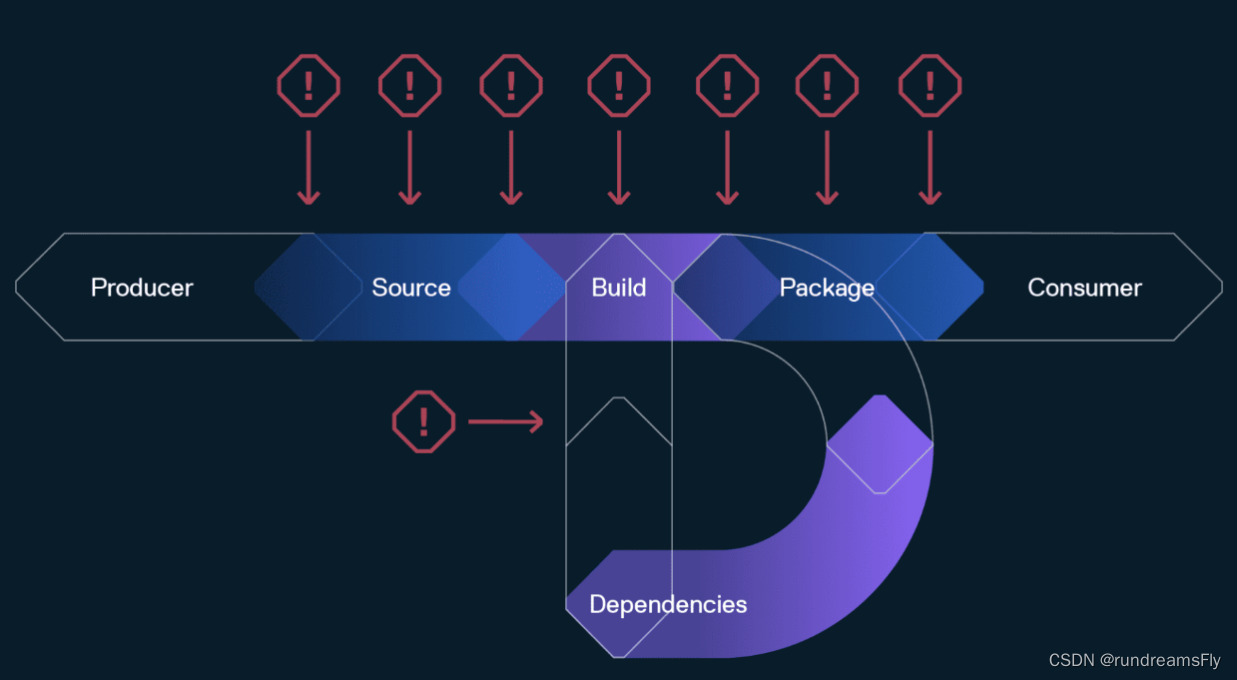
【云原生-制品管理】制品管理的优势
制品介绍制品管理-DevOps制品管理优势总结 制品介绍 制品管理指的是存储、版本控制和跟踪在软件开发过程中产生的二进制文件或“制品”的过程。这些制品可以包括编译后的源代码、库和文档,包括操作包、NPM 和 Maven 包(或像 Docker 这样的容器镜像&…...
)
Java爬虫----HttpClient方式(获取数据篇)
目录 一、爬虫的定义 二、获取数据 (1)基于Get方式的请求(无参) (2)基于Get方式请求(有参) (3)基于Post方式的请求(无参) &…...

计算机视觉实验:图像增强应用实践
本次实验主要从基于统计、函数映射的图像增强方法和基于滤波的图像增强方法两种方法中对一些图像增强的算法进行实现。主要的编程语言为python,调用了python自带的PIL图像库用于读取图像,利用numpy进行图像运算,最后使用opencv第三方库进行对…...

ES6:Generator函数详解
ES6:Generator函数详解 1、 概念2、yield表达式2.1 yield 语句与 return 语句区别2.2 Generator函数不加yield语句,这时变成了一个单纯的暂缓执行函数2.3 yield 表达式只能用在 Generator 函数里面,用在其它地方都会报错2.4 yield 表达式如果…...
前端小练-产品宣传页面
文章目录 前言页面结构固定钉头部轮播JS特效 完整代码总结 前言 经过一个月的爆肝,花费了一个月(期间还花费了将近半个月的时间打比赛,还要备研)算是把数二高数的内容强化了一遍,接下来刷熟练度即可,可惜的…...

arm学习之stm32设备树学习-中断控制led灯亮灭+字符设备指令控制led灯亮灭
中断控制led灯亮灭 驱动文件源码 led-key.c #include<linux/init.h> #include<linux/module.h> #include<linux/of.h> #include<linux/of_gpio.h> #include<linux/gpio.h> #include<linux/of_irq.h> #include<linux/interrupt.h> s…...
快速开发框架若依的基础使用详解
Hi I’m Shendi 快速开发框架若依的基础使用详解 最近在为公司制作新的项目,经过了一段时间的技术沉淀,我开始尝试接触市面上用的比较多的快速开发框架,听的最多的当属若依吧 于是就选用了若依 介绍 为什么选?目的是为了提高开发…...

RabbitMQ 教程 | 第4章 RabbitMQ 进阶
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是 DevO…...
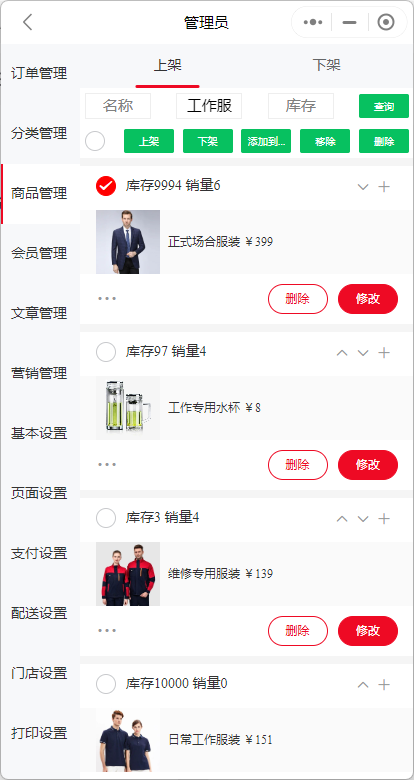
小程序如何从分类中移除商品
有时候商家可能需要在商品分类中删除某些商品,无论是因为商品已下架、库存不足还是其他原因。在这篇文章中,我们将介绍如何从分类中移除商品。 方式一:分类管理中删除商品。 进入小程序管理后台,找到分类管理,在分…...

P1219 [USACO1.5] 八皇后 Checker Challenge
题目 思路 非常经典的dfs题,需要一点点的剪枝 剪枝①:行、列,对角线的标记 剪枝②:记录每个皇后位置 代码 #include<bits/stdc.h> using namespace std; const int maxn105; int a[maxn];int n,ans; bool vis1[maxn],vis…...
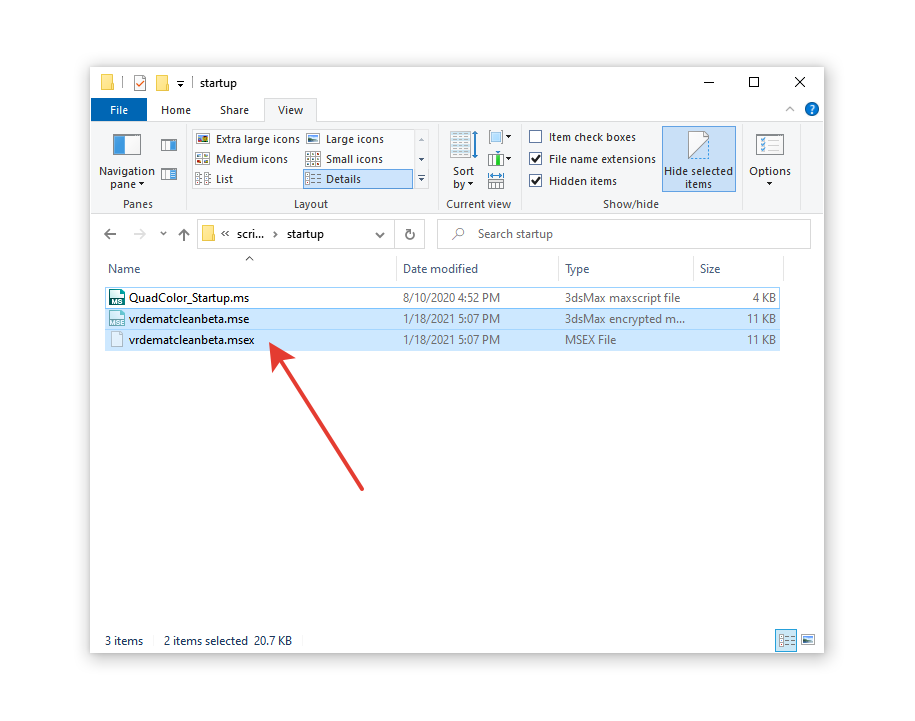
如何在不使用脚本和插件的情况下手动删除 3Ds Max 中的病毒?
如何加快3D项目的渲染速度? 3D项目渲染慢、渲染卡顿、渲染崩溃,本地硬件配置不够,想要加速渲染,在不增加额外的硬件成本投入的情况下,最好的解决方式是使用渲云云渲染,在云端批量渲染,批量出结…...
SpringCloud Gateway 在微服务架构下的最佳实践
作者:徐靖峰(岛风) 前言 本文整理自云原生技术实践营广州站 Meetup 的分享,其中的经验来自于我们团队开发的阿里云 CSB 2.0 这款产品,其基于开源 SpringCloud Gateway 开发,在完全兼容开源用法的前提下&a…...
Android studio修改app图标
步骤如下: 1.右键app名称→New→ImageAsset 2. 进行下面的配置 图源:https://blog.csdn.net/Qingshan_z/article/details/126661650 3.配置分辨率 4.图标自动保存在mipmap文件夹下 再启动就更换成功了!!! 参考&…...

<C++> 三、内存管理
1.C/C内存分布 我们先来看下面的一段代码和相关问题 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] {1, 2, 3, 4};char char2[] "abcd";const char *pChar3 "abcd";int *ptr1…...
大模型开发(十五):从0到1构建一个高度自动化的AI项目开发流程(上)
全文共5600余字,预计阅读时间约13~20分钟 | 满满干货(附全部代码),建议收藏! 本文目标:提出一种利用大语言模型(LLMs)加快项目的开发效率的解决思路,本文作为第一部分,主要集中在如何完整的执行引导Chat模…...

HarmonyOS 开发基础(二)组件拼凑简单登录页面
一、简单登录页面 Entry Component /* 组件可以基于struct实现,组件不能有继承关系,struct可以比class更加快速的创建和销毁。*/ struct Index {State message: string Hello Worldbuild() {// https://developer.harmonyos.com/cn/docs/documentation/…...
flutter minio
背景 前端 经常需要上传文件 图片 视频等等 到后端服务器, 如果到自己服务器 一般会有安全隐患。也不方便管理这些文件。如果要想使用一些骚操作 比如 按照前端请求生成不同分辨率的图片,那就有点不太方便了。 这里介绍以下 minio,࿰…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
