机器学习-New Optimization
机器学习(New Optimization)
前言:
学习资料
| video | ppt | blog |
|---|
下面的PPT里面有一些符号错误,但是我还是按照PPT的内容编写公式,自己直到符号表示什么含义就好了
Notation
| 符号 | 解释 |
|---|---|
| θ t \theta_t θt | 第 t 步时,模型的参数 |
| Δ L ( θ ) \Delta L(\theta) ΔL(θ) or g t g_t gt | 模型参数为 θ t \theta_t θt 时,对应的梯度,用于计算 θ t + 1 \theta_{t+1} θt+1 |
| m t + 1 m_{t+1} mt+1 | 从第 0 步到第 t 步累计的momentum,用于计算 θ t + 1 \theta_{t+1} θt+1 |

On-line VS Off-line
- On-line:每次参数更新,只给一对 ( x t x_t xt , y t y_t yt )
- Off-line:每次更新参数,考虑所有的训练资料
常用优化算法
intention:
- Find a 𝜃 to get the lowest ∑ x L ( θ ; x ) \sum_x L(\theta; x) ∑xL(θ;x) !!
- Or, Find a 𝜃 to get the lowest L ( θ ) L(\theta) L(θ) !!
1. 随机梯度下降法(SGD,Stochastic gradient descent)
算法思想:少量多次
- GD算法进行梯度更新的时候,一般都使所有数据训练完成以后才进行一次更新,每一次都是对参数进行一大步的更新
- SGD算法每次选取其中的一个样本进行梯度的计算,然后再进行参数的更新,每一次都是对参数进行一小步的更新
注意
- SGD随机梯度下降本质是只取一个样本来计算梯度,避免了梯度下降用全部样本计算梯度的大量运算,而在上面的代码里的loss.backward()会使用全部样本来计算梯度,可以去看看这个问答
- 先在的主流框架中所谓的SGD实际上都是Mini-batch Gradient Descent (MBGD,亦成为SGD)。对于含有N个训练样本的数据集,每次参数更新,仅依据一部分数据计算梯度。小批量梯度下降法既保证了训练速度,也保证了最后收敛的准确率。
图解:
2. SGD with Momentum (SGDM)
算法思想:在SGD的基础上,考虑前一次更新的梯度。
- 将前面的梯度考虑在内,防止出现局部最优解
- Local Minimum,此时的gradient是0,但是不是全局最优解,如果我们考虑前面的梯度的history,那么他会继续优化前进,达到更好的效果
算法:
- 参数: θ t \theta^t θt
- 梯度: Δ L ( θ t ) \Delta L(\theta^t) ΔL(θt)
- 移动:
- v 0 = 0 v^0 = 0 v0=0
- v t + 1 = λ v t + η Δ L ( θ t ) v^{t+1} = \lambda v^t + \eta \Delta L(\theta^t) vt+1=λvt+ηΔL(θt)
- 参数更新: θ t + 1 = θ t + v t + 1 \theta^{t+1} = \theta^t + v^{t+1} θt+1=θt+vt+1
Movement not just based on gradient, but previous movement
图解:
Why momentum?
- Momentum即动量,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。这样一来,可以在一定程度上增加稳定性,从而学习地更快,并且还有一定摆脱局部最优的能力
- 防止局部最优解
- 在进入梯度为0的地方,并不会马上停下来,而因为gradient of previous 而继续前进
3. Adagrad
算法思想:根据所有的梯度自行调整学习率,使得模型在较短的时间内达到较好的收敛效果
算法:
θ t = θ t − 1 − η ∑ i = 0 t − 1 ( g i ) 2 g t − 1 \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\sum_{i=0}^{t-1}(g_i)^2}} g_{t-1} θt=θt−1−∑i=0t−1(gi)2ηgt−1
优缺点:
- 优点:
- 自适应学习率,根据每个参数的历史梯度信息调整学习率,有助于更稳定地收敛。
- 不需要手动调整学习率,适应不同参数的更新频率。
- 适用于稀疏数据,对出现频率较低的参数使用较大的学习率。
- 缺点:
- 学习率逐渐减小可能导致学习率过小,使得模型停止学习或更新过于缓慢。
- 对非凸优化问题可能表现不佳,难以跳出局部最小值。
- 内存开销较大,对大规模模型和数据集可能不适用。
图解:
4. RMSProp(Root Mean Square Propagation)
算法思想:实现学习率的自动更新
- 用微分平方移动加权平均解决了vt一直增大,防止在t很大以后,系数太小,无法走出去的问题。vt如果是前t个gradient的平方和,分母会永无止境的增加。
- 与Adagrad一致,但解决了Adagrad的缺点
算法:
- v 1 = g 0 2 v_1 = g_0^2 v1=g02
- v t = α v t − 1 + ( 1 − α ) g t − 1 2 v_t = \alpha v_{t-1} + (1 - \alpha)g_{t-1}^2 vt=αvt−1+(1−α)gt−12
- θ t = θ t − 1 − η v t g t − 1 \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{v_t}}g_{t-1} θt=θt−1−vtηgt−1
- α \alpha α:衰减因子(一般取值较接近1,如0.9)
优缺点:
- 优点:
- 自适应学习率,可以在训练过程中调整学习率,有助于稳定收敛。
- 解决Adagrad的学习率衰减问题,避免学习率过小导致停止学习。
- 在非凸优化问题中表现良好,有助于跳出局部最小值。
- 适用于大规模模型和数据集,内存开销较小。
- 缺点:
- 学习率仍可能衰减过快,导致收敛较慢。
- 对于不同问题,对超参数敏感,需要调参。
- 不适用于稀疏数据。
图解:
5. Adam(Adaptive Moment Estimation)
算法思想:将SGDM与RMSProp合在一起使用
算法:
- m t = β 1 m t − 1 + ( 1 − β 1 ) g t ( 1 ) m_t = \beta_1m_{t-1} + (1 - \beta_1)g_t \qquad(1) mt=β1mt−1+(1−β1)gt(1)
- v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 ( 2 ) v_t = \beta_2v_{t-1} + (1 - \beta_2)g_t^2 \qquad(2) vt=β2vt−1+(1−β2)gt2(2)
- m ^ t = m t 1 − β 1 t ( 3 ) \widehat{m}_t = \frac{m_t}{1 - \beta_1^t} \qquad(3) m t=1−β1tmt(3)
- v ^ t = v t 1 − β 2 t ( 4 ) \widehat{v}_t = \frac{v_t}{1 - \beta_2^t} \qquad(4) v t=1−β2tvt(4)
- θ t = θ t − 1 − η v ^ t + ε m ^ t ( 5 ) \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\widehat{v}_t + \varepsilon}}\widehat{m}_t \qquad(5) θt=θt−1−v t+εηm t(5)
注解:
- 公式(1)取自SGDM算法,保留了Momentum即动量,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。
- m t m_t mt是本次的Momentum
- m t − 1 m_{t-1} mt−1是上一次的Momentum
- g t g_t gt是本次的梯度
- β 1 \beta_1 β1是超参数,默认为0.9。通过修改这个参数实现前面动量对后面动向的影响。
- β 1 \beta_1 β1看起感觉只考虑了0.1的本次梯度,考虑了0.9的历史梯度,但本次梯度会在下次更新时被考虑进来。
- 公式(2)取自RMSProp算法, β 2 \beta_2 β2是超参数,默认0.999。
- 公式(3)和(4)是分别对 m t m_t mt和 v t v_t vt进行了放大,而且是放大得越来越少。
注意:Adam算法中的矩变量(一阶矩估计m和二阶矩估计v)在训练的初期可能会有偏差。这是因为在初始时,这些变量会被初始化为零,导致它们在训练初期偏向于较小的值。- 公式(5)是我们最后更新的公式,分母加入 ε \varepsilon ε是为了防止分母为0,一般很小,默认 1 0 − 8 10^{-8} 10−8.
- 矩:通过这种方式,Adam算法能够更快地收敛并避免陷入局部最小值。
- 一阶矩变量m类似于动量的作用,有助于平滑梯度更新方向;
- 二阶矩变量v类似于RMSProp的作用,对历史梯度平方进行衰减,适应不同参数的更新频率。
优缺点:
- 优点:
- 自适应学习率,稳定收敛,适应不同参数的更新频率。
- 综合了动量和自适应学习率,高效优化模型参数。
- 适用于稀疏数据和大规模模型,内存开销较小。
- 缺点:
- 对非平稳目标函数可能不稳定。
- 对超参数敏感,需要调参。
图解:
6. AMSGrad(Adaptive Moment Estimation with Slower Learning Rates)
算法思想:与Adam算法基本一样(Adam算法的优化)
调整:二阶矩变量(自适应学习率)
v ^ t = m a x ( v ^ t − 1 , v t ) \widehat{v}_t = max(\widehat{v}_{t-1},v_t) v t=max(v t−1,vt)
在对二阶矩变量进行纠正之前,先与前一次纠正后的二阶矩变量进行大小比较,直接赋值给纠正后的二阶矩变量,然后在对纠正后的二阶矩变量再进行纠正
算法:
- m t = β 1 m t − 1 + ( 1 − β 1 ) g t ( 1 ) m_t = \beta_1m_{t-1} + (1 - \beta_1)g_t \qquad(1) mt=β1mt−1+(1−β1)gt(1)
- v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 ( 2 ) v_t = \beta_2v_{t-1} + (1 - \beta_2)g_t^2 \qquad(2) vt=β2vt−1+(1−β2)gt2(2)
- v ^ t = m a x ( v ^ t − 1 , v t ) ( 3 ) \widehat{v}_t = max(\widehat{v}_{t-1},v_t) \qquad(3) v t=max(v t−1,vt)(3)
- m ^ t = m t 1 − β 1 t ( 4 ) \widehat{m}_t = \frac{m_t}{1 - \beta_1^t} \qquad(4) m t=1−β1tmt(4)
- v ^ t = v ^ t 1 − β 2 t ( 5 ) \widehat{v}_t = \frac{\widehat{v}_t}{1 - \beta_2^t} \qquad(5) v t=1−β2tv t(5)
- θ t = θ t − 1 − η v ^ t + ε m ^ t ( 6 ) \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\widehat{v}_t + \varepsilon}}\widehat{m}_t \qquad(6) θt=θt−1−v t+εηm t(6)
优缺点:
- 优点:
- 防止学习率过大,更稳定地收敛。
- 适用于不同问题,在某些复杂的优化问题中表现优于Adam算法。
- 缺点:
- 需要额外的存储开销,可能增加内存需求。
- 需要调参,同样需要调节学习率和衰减因子等超参数。
7. SWATS(Simply combine Adam with SGDM)
算法思想:将Adam算法和SGDM(随机梯度下降法与动量)算法简单地结合在一起的优化算法。
- 在SGDM中,动量被用来加速优化过程,通过将上一次的更新的一部分加到当前的更新中,帮助算法在某个方向上“保持运动”,从而加快收敛速度。
- Adam算法结合了自适应学习率和动量的优点。它根据历史梯度信息为每个参数自适应地调整学习率,从而在不同场景下实现更高效的优化。
- 在SWATS算法中,主要思想是同时使用Adam的自适应学习率和SGDM的动量。通过这样做,算法可以充分利用Adam对每个参数使用不同学习率的能力,以及SGDM的加速特性。
8. RAdam(Rectified Adam)
算法思想:
算法:
- 初始化:设置学习率 α \alpha α,一阶矩估计的衰减因子 β 1 \beta_1 β1和二阶矩估计的衰减因子 β 2 \beta_2 β2,并初始化一阶矩变量 m m m和二阶矩变量 v v v。
- 计算梯度:计算当前迭代的梯度 g t = ∇ θ L ( θ ) g_t = \nabla_{\theta} L(\theta) gt=∇θL(θ)。
- 更新一阶矩变量:计算一阶矩估计 m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t mt=β1mt−1+(1−β1)gt。
- 更新二阶矩变量:计算二阶矩估计 v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 vt=β2vt−1+(1−β2)gt2。
- 计算修正后的一阶矩估计:计算修正后的一阶矩估计 m ^ t = m t 1 − β 1 t \widehat m_t = \frac{m_t}{1 - \beta_1^t} m t=1−β1tmt。
- 计算修正项 ρ \rho ρ:计算 ρ = ( 2 − β 2 t ) ( 1 − β 2 t ) \rho = \sqrt{\frac{(2 - \beta_2^t)}{(1 - \beta_2^t)}} ρ=(1−β2t)(2−β2t)。
- 计算修正后的学习率:计算修正后的学习率 l r t = α ρ lr_t = \alpha \rho lrt=αρ。
- 计算RAdam更新量:如果 v ^ t = max ( v ^ t − 1 , v t ) \widehat v_t = \max(\widehat v_{t-1}, v_t) v t=max(v t−1,vt),则 r t = l r t m ^ t v ^ t + ϵ r_t = \frac{lr_t \widehat m_t}{\sqrt{\widehat v_t} + \epsilon} rt=v t+ϵlrtm t,否则 r t = l r t m t v t + ϵ r_t = \frac{lr_t m_t}{\sqrt{v_t} + \epsilon} rt=vt+ϵlrtmt。
- 更新参数: θ t = θ t − 1 − r t \theta_t = \theta_{t-1} - r_t θt=θt−1−rt。
优缺点:
- 优点:
- 稳定性改进:修正学习率在训练初期的偏差,提高了算法的稳定性,更容易收敛。
- 自适应学习率:无需手动调节学习率,算法能够自适应地调整学习率。
- 高效:在大规模模型和数据集上具有较快的收敛速度。
- 缺点:
- 适用性限制:对于某些问题可能不如其他优化算法效果好。
- 需要额外存储开销:算法需要额外存储梯度平方估计的历史信息,增加一些内存开销。
- 需要调参:虽然不需手动调节学习率,但仍需调节其他超参数以获得最佳性能。
相关文章:

机器学习-New Optimization
机器学习(New Optimization) 前言: 学习资料 videopptblog 下面的PPT里面有一些符号错误,但是我还是按照PPT的内容编写公式,自己直到符号表示什么含义就好了 Notation 符号解释 θ t \theta_t θt第 t 步时,模型的参数 Δ L …...

3d虚拟vr汽车实景展厅吸引更多潜在消费者
随着人们对生活品质的追求,越来越多的消费者开始关注汽车的外观设计、内饰配置等方面。传统的展示方式已经不能满足消费者的需求,车辆VR虚拟漫游展示应运而生。借助VR虚拟现实和web3d开发建模技术,对汽车的外观、造型及信息数据进行数字化处理…...

Java里的static import使用小结
Java里的static import使用小结 换了工作要把Java重新捡起来了,这个在大学里用过的语言,虽然不复杂,还是有一些奇怪的地方的。比如static Slgluimport。 Static import是JDK 1.5中引进的特性,不过读大学那会还真没注意到。它的作…...
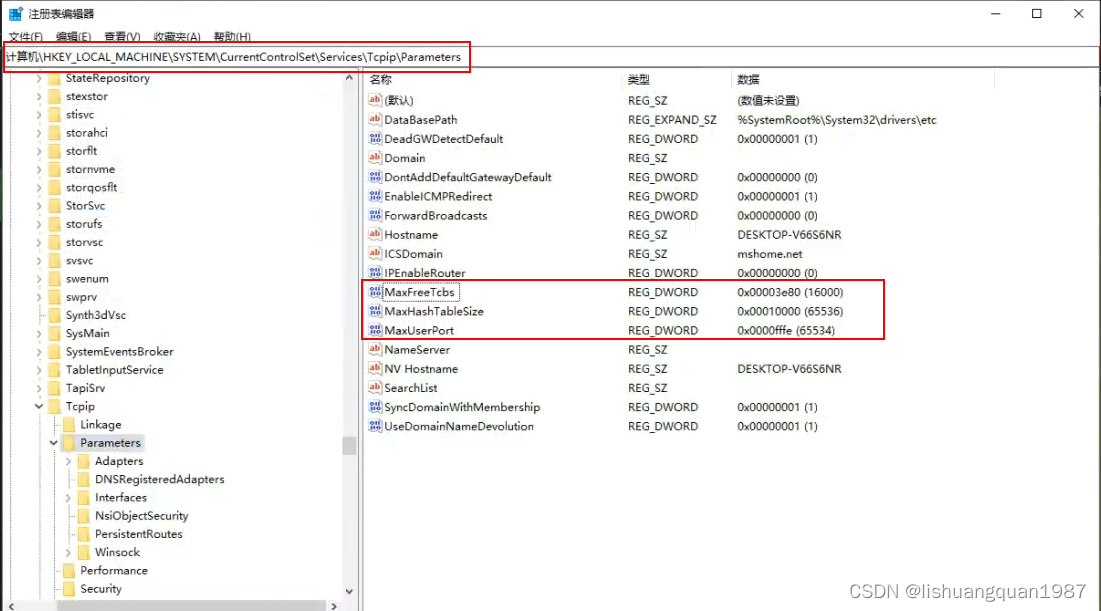
go程序使用tcp短连接报:only one usage of each socket address
环境及现象 Win10上位机(C#,WPF)后台使用go作为服务。 连接情况 C#连接大概60个TCP长连接(设备)。 后台go服务连接60个UDP短连接(设备附属硬件), 10个TCP短连接(PLC,modbus通讯&a…...
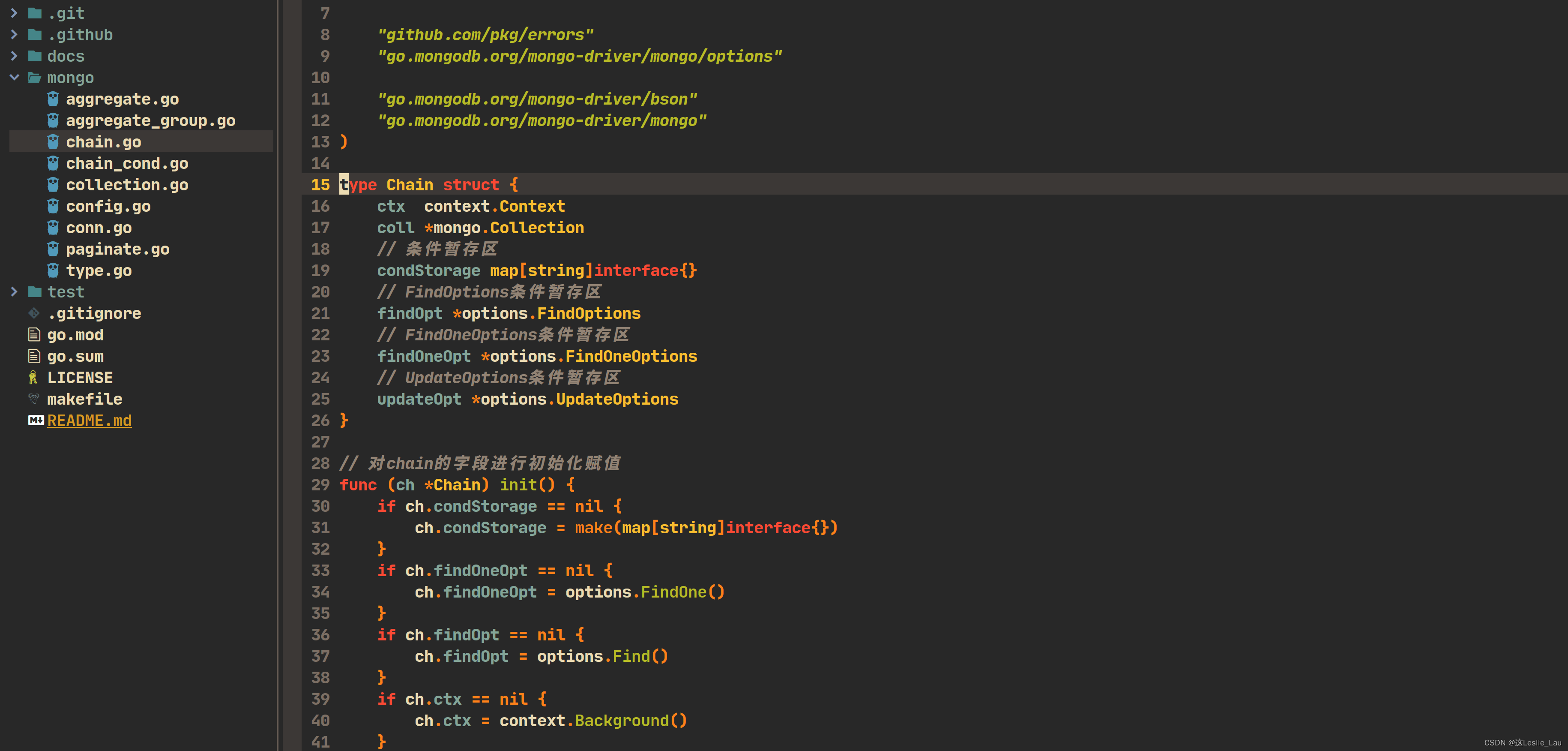
十分钟配置好Neovim go开发环境(其他语言一样)
文章目录 前言仓库地址用法快捷键问题反馈 前言 这篇文章的目的是为了分享下我自己的Neovim配置。 本人是Golang程序员,最开始使用的IDE是JetBrains Goland。有一说一这个ide适配度很高,认识的很多人都使用这个。但是它也有几个对我来说的缺点…...
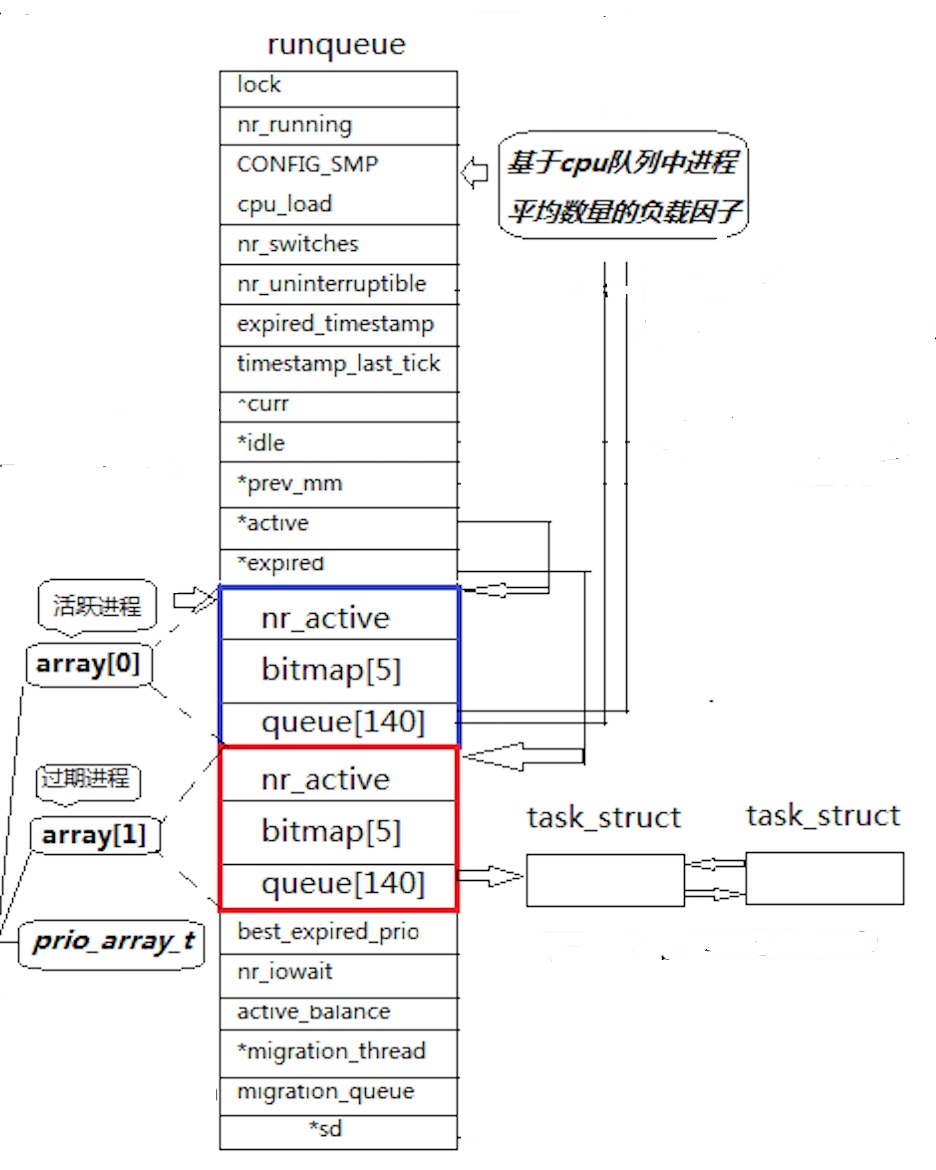
Linux第八章之进程概念
一、冯诺依曼体系结构 关于冯诺依曼,必须强调几点: 这里的存储器指的是内存不考虑缓存情况,这里的CPU能且只能对内存进行读写,不能访问外设(输入或输出设备)外设(输入或输出设备)要输入或者输出数据,也只能写入内存或…...

怎么学习Java并发编程相关技术? - 易智编译EaseEditing
学习Java并发编程可以通过多种方式进行,包括但不限于以下几种: 在线教程和学习平台: 网上有许多免费和付费的Java并发编程教程和学习平台,如Coursera、Udemy、edX、Codecademy等。这些平台提供结构化的课程和练习,适…...

vue3 +element动态表单实现
可以直接复制,接口看后端 父页面 <schedulesref"schedulesRef":dxbz"props.dxbz":jdlx"props.jdlx":woId"myWoId":addendumList"formInline.addendumList"v-if"addendumShow"addendum"addendu…...

Linux部署jar包,隐藏命令行参数
Linux部署jar包,隐藏命令行参数 一、背景需求二、查阅资料三、实现隐藏库3.1、测试test.c3.2、设置隐藏库3.3、验证 四、应用jar启动命令五、直接应用结果 最新项目安全检测,发现配置文件中数据库密码,redis密码仍处理明文状态 于是整理了一篇…...
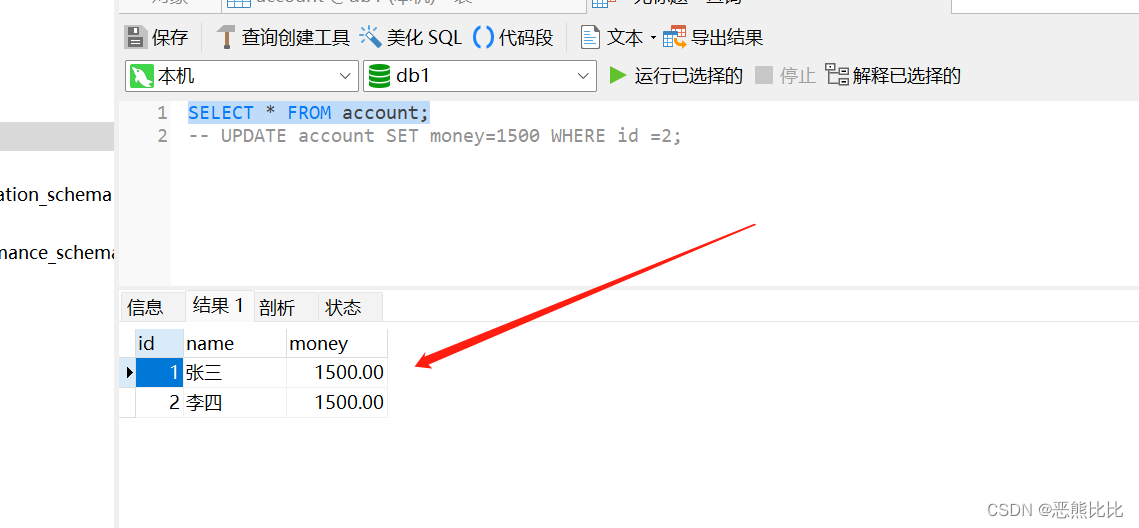
JDBC-笔记
JDBC 1. JDBC介绍 JDBC(Java Database Connectivity)是一种用于连接和操作数据库的 Java API。 通过Java操作数据库的流程 第一步:编写Java代码 第二步:Java代码将SQL发送到MySQL服务端 第三步:MySQL服务端接收到SQ…...
)
Rust的入门篇(中)
Rust的入门篇(中) 这是接上面一篇rust入门篇(上)文章 22. 包管理一 mod nation {pub mod government {pub fn govern() {}}mod congress {pub fn legislate() {}}mod court {fn judicial() {super::congress::legislate();}} }fn main() {nation::government::govern(); }23.…...

手机设置全局代理ip步骤
在互联网时代,隐私和安全问题备受关注。使用全局代理能够帮助我们保护个人信息,突破地理限制,并提高网络速度。但是,你是否对全局代理的安全性存有疑虑?而且,如何在手机上设置全局代理呢?今天就…...

spring boot+thymeleaf+semantic ui 分页
参考: https://my.oschina.net/ayyao/blog/898041 后端 springboot 使用: com.github.pagehelper.PageInfo,作为分页对象 <!--引入分页插件--> <dependency><groupId>com.github.pagehelper</groupId><artifa…...
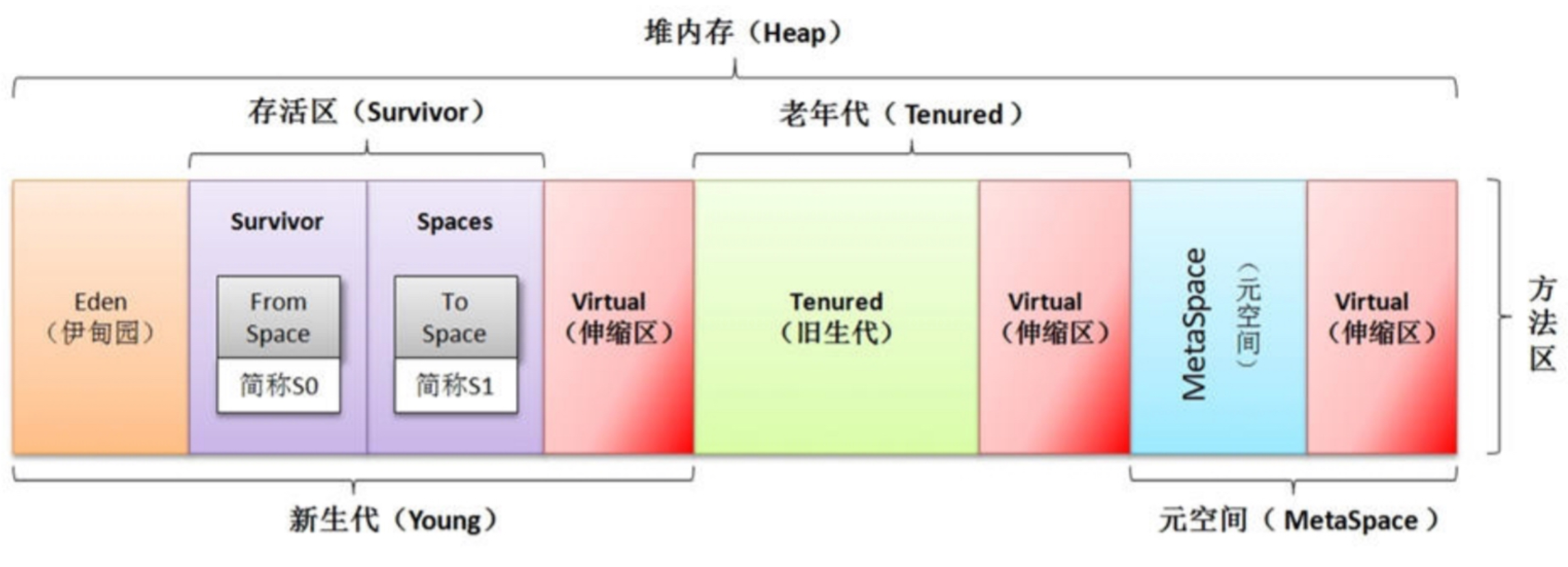
【JVM】(一)深入理解JVM运行时数据区
文章目录 一、JVM 运行流程二、虚拟机栈(线程私有)三、本地方法栈 (线程私有)四、方法区(元数据区)五、堆(线程共享)六、程序计数器(线程私有) 一、JVM 运行流…...

C++ QRegExpValidator
//正在表达式限制输入 QString str "\\b(?:(?:25[0-5]|2[0-4][0-9]|[01]?[0-9][0-9]?)\\.){3}(?:25[0-5]|2[0-4][0-9]|[01]?[0-9][0-9]?)\\b"; ui->lineEdit->setValidator(new QRegExpValidator(QRegExp(str))); //用于占位 ui->lineEdit->setI…...
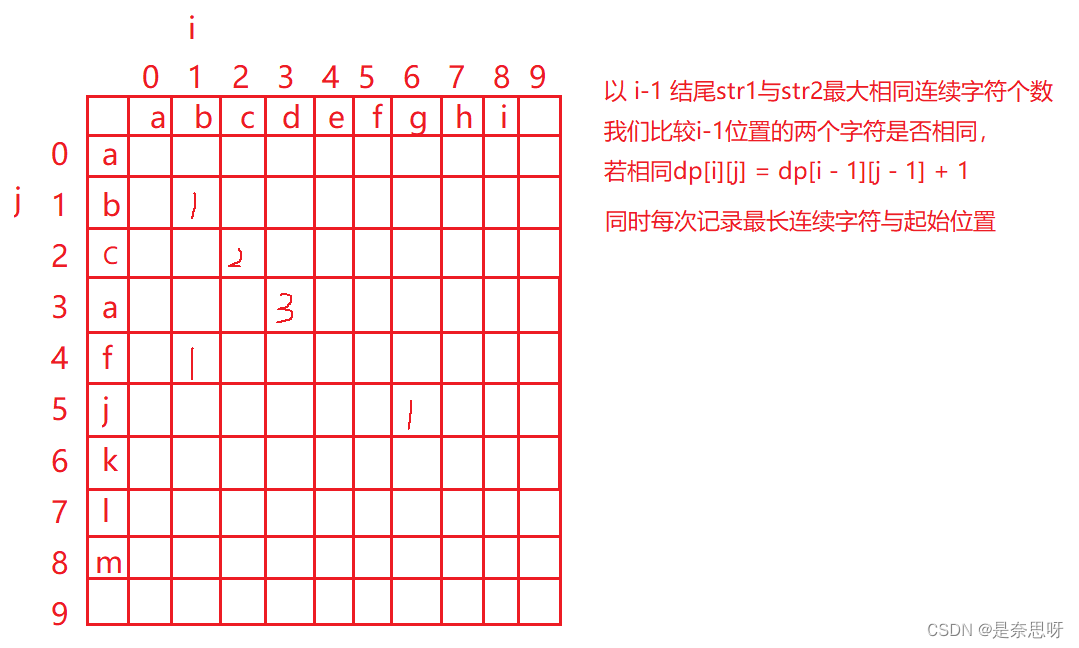
备战秋招 | 笔试强训19
目录 一、选择题 二、编程题 三、选择题题解 四、编程题题解 一、选择题 1、二分查找的时间复杂度() A. O(N*log(N)) B. O(N) C. O(log(N)) D. O(N^2) 2、有一个单向链表中有一个A、B两个相邻元素,有一个指针p指向元素A,现将…...

第一章 计算机网络概述
第一章 计算机网络概述 1.1 计算机网络在信息时代的作用 1.2 因特网概述 网络分类: 网络:许多计算机连接在一起的的局域网; 互联网:internet许多网络连接在一起; 因特网:Internet 全球最大的互联网&…...
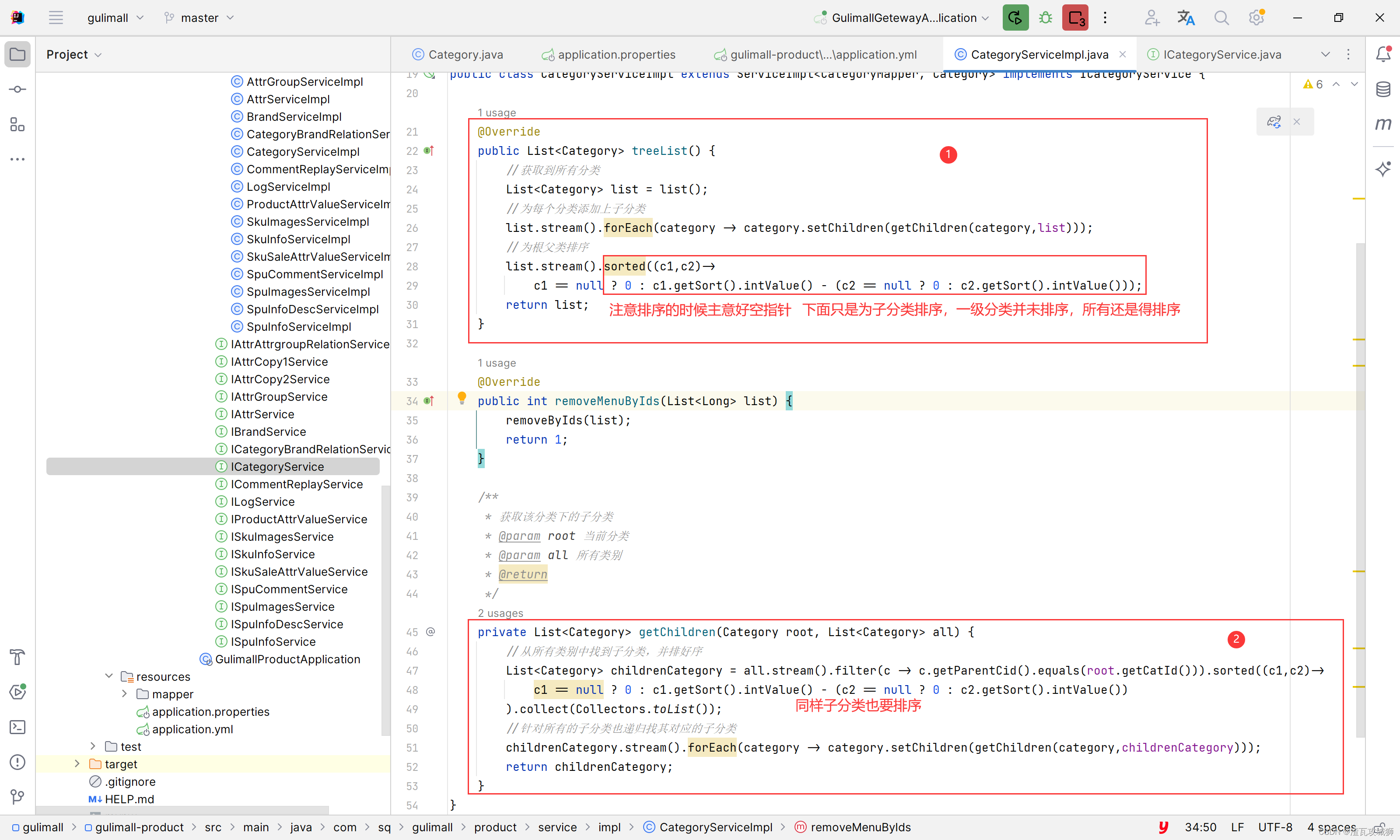
谷粒商城第六天-商品服务之分类管理下的获取三级分类树形列表
目录 一、总述 1.1 前端思路 1.2 后端思路 二、前端部分 2.1 在网页中建好目录及菜单 2.1.1 建好商品目录 2.1.2 建好分类管理菜单 编辑 2.2 编写组件 2.2.1 先完成组件文件的创建 2.2.2 编写组件 2.2.2.1 显示三级分类树形列表 三、后端部分 3.1 编写商品分类…...
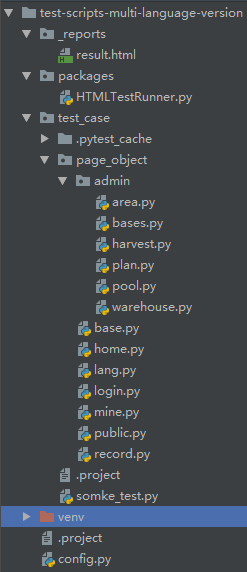
【UI自动化测试】Appium+Python+Unittest+HTMLRunner
简介 获取AppPackage和AppActivity 定位UI控件的工具 脚本结构 PageObject分层管理 HTMLTestRunner生成测试报告 启动appium server服务 以python文件模式执行脚本生成测试报告 【B站最通俗易懂】Python接口自动化测试从入门到精通,超详细的进阶教程,看完…...

【限时优惠】红帽openstack管理课程(CL210) 即将开课
课程介绍 通过实验室操作练习,学员将能够深入学习红帽企业 Linux OpenStack 平台各服务的手动安装方法,还将了解 OpenStack 开发社区的未来发展计划。 培训地点: 线下面授:苏州市姑苏区干将东路666号401室; 远程…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...







