Java 中为什么要把一个数模(10^9+7)
在计算机科学和编程中,经常会遇到需要对结果进行取模操作的情况。模运算是指将一个数除以另一个数,并取得余数的运算。
在 Java 中,常见的一个数取模的值是 (10^9+7),即 1000000007。这个特定的数值经常在算法和数学计算中被使用,有以下几个原因:
-
防止整数溢出:在计算过程中,一些中间结果或最终结果可能会非常大,超出整数的表示范围。通过对结果进行取模操作,可以将结果限制在一个合理的范围内,避免溢出。
-
处理大数运算:有时候需要进行大数运算,例如计算组合数、排列数等。对于这些计算,结果往往非常巨大,无法用常规的数据类型表示。通过取模操作,可以将结果转换为相对较小的数值,方便处理和比较。
-
保持结果一致性:在一些算法和计算中,需要确保结果的一致性和可比性。由于取模操作的结果始终在一个固定的范围内,可以保证不同计算之间的结果具有可比性,并且便于进行进一步的操作和分析。
-
避免数值误差:在浮点数运算中,存在舍入误差和精度问题。通过取模操作,可以将浮点数运算转换为整数运算,避免了数值误差的问题。
注意,(10^9+7) 是一个常用的取模值,但并不是所有情况下都可以使用,具体取模值的选择取决于问题的特性和要求。
相关文章:
)
Java 中为什么要把一个数模(10^9+7)
在计算机科学和编程中,经常会遇到需要对结果进行取模操作的情况。模运算是指将一个数除以另一个数,并取得余数的运算。 在 Java 中,常见的一个数取模的值是 (10^97),即 1000000007。这个特定的数值经常在算法和数学计算中被使用&…...

RPC与REST有什么区别?
原文:RPC与REST有什么区别? 背景 好多开发的同学在工作中,经常分不清RPC和REST的区别,导致经常沟通不在一个层次上。甚至有些同学把这两个当成同一个东西。 RPC与REST的区别? 对比名称 rpc rest 备注 架构风格 RP…...
时间复杂度介绍及其计算
时间复杂度 1.算法效率 如何衡量一个算法的好坏呢?看这段代码: long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) Fib(N-2); }这是斐波那契数列的递归代码,非常简洁,那么这就一定说明它好吗?答案显而易…...
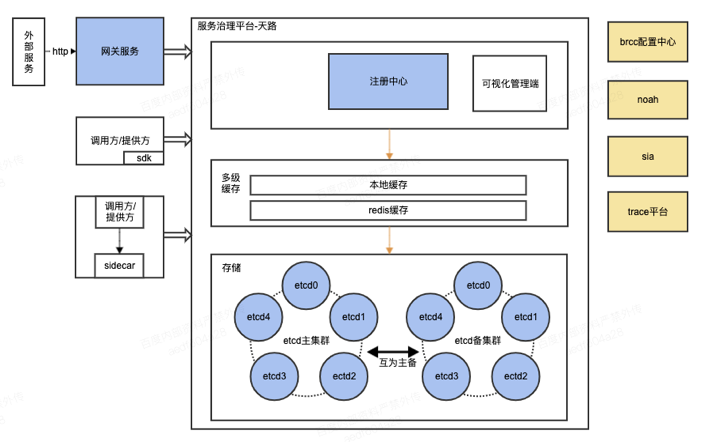
etcd实现大规模服务治理应用实战
导读:服务治理目前越来越被企业建设所重视,特别现在云原生,微服务等各种技术被更多的企业所应用,本文内容是百度小程序团队基于大模型服务治理实战经验的一些总结,同时结合当前较火的分布式开源kv产品etcd,…...

目标检测中 anchor base和anchor free
目标检测中两种不同anchor的生成 趋势:anchor free越来越受到实时性检测的青睐,,,...

TypeC拓展设计方案|TypeC转HDMI设计方案|CS5261/CS5265芯片设计参数对比
集睿智远CS5261/CS5265都可以用于设计TypeC转HDMI方案,低成本TypeC扩展坞设计方案,而两者也有些差异:1.CS5261支持DP1.4输入,一个HDMI1.4输出,即HDMI输出为4K30HZ ;CS5265DP1.4到HDMI2.0转换芯片,即HDMI输出…...
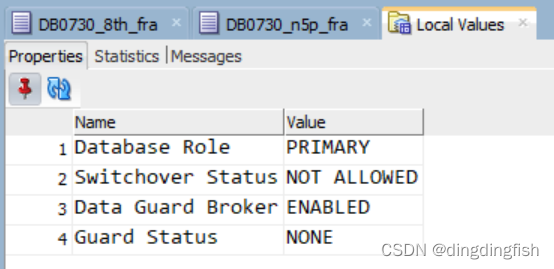
SQL Developer中的Active Data Guard
这篇文章 Display Data Guard configuration in SQL Developer 中,用SQL Developer展示了多种ADG的拓扑。 今天自己也试了一下,还蛮简单的,其实最麻烦的部分在于搭建一个ADG环境。 假设我已有一个ADG环境,即最典型的环境&#x…...

谈谈FFT到底有何用
谈谈FFT到底有何用 FFT快速傅里叶变换是数字信号处理的经典算法,学过DSP或者芯片设计的人大多知道这个算法;但是,大家是否想过,为什么数字信号处理会有那么多FFT呢有人会说,为了分析信号的频谱;那么下边的问题就是,分析频谱对我们的日常需求,比如手机打电话,雷达测量速度和方向…...
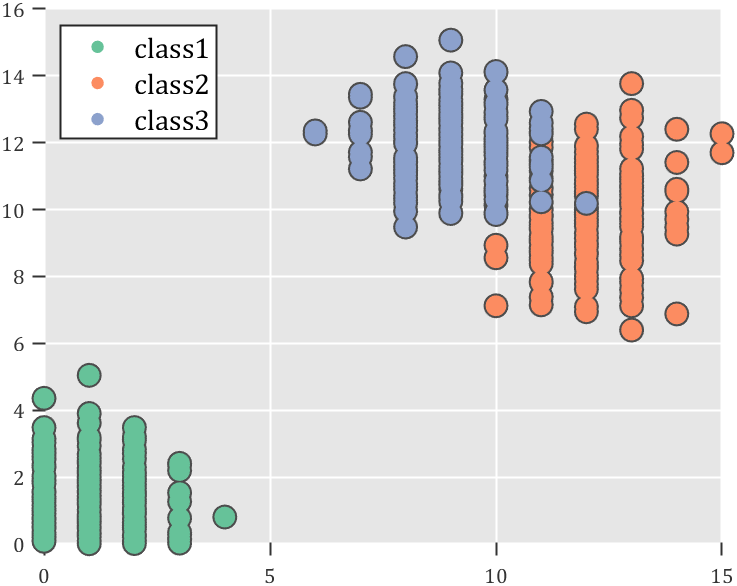
MATLAB | 如何绘制这样的描边散点图?
part.-1 前前言 最近略忙可能更新的内容会比较简单,见谅哇,今日更新内容: part.0 前言 看到gzhBYtools科研笔记(推荐大家可以去瞅瞅,有很多有意思的图形的R语言复现!!)做了这样一张图: 感觉很…...

偶数科技与白鲸开源完成兼容性认证
近日,偶数科技自主研发的云原生分布式数据库 OushuDB v5.0 完成了与白鲸开源集成调度工具 WhaleStudio v2.0 的兼容性相互认证测试。 测试结果显示,双方产品相互良好兼容,稳定运行、安全,同时可以满足性能需求,为企业级…...
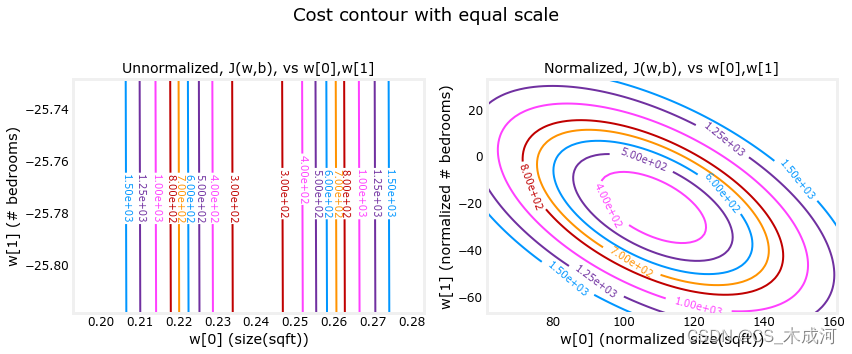
【机器学习】Feature scaling and Learning Rate (Multi-variable)
Feature scaling and Learning Rate 1、数据集2、学习率2.1 α \alpha α 9.9e-72.2 α \alpha α 9e-72.3 α \alpha α 1e-7 3、特征缩放3.1 特征缩放的原因3.2 Z-score 归一化3.3 预测3.4 损失等值线 导入所需的库 import numpy as np np.set_printoptions(precision…...
windows编译ncnn
官方代码https://github.com/Tencent/ncnn/wiki/how-to-build#build-for-windows-x64-using-visual-studio-community-2017 编译工具 visual studio 2017 一、编译protobuf 1、下载protobuf protobuf-3.11.2:https://github.com/google/protobuf/archive/v3.11…...

C++和Lua交互总结
C和Lua交互总结 Chapter1. C和Lua交互总结一、Lua与C的交互机制——Lua堆栈二、堆栈的操作三、C 调用 Lua1)C获取Lua值2)C调用Lua函数示例: 四、Lua 调用 C包装C函数 最后总结一下 Chapter1. C和Lua交互总结 原文链接:https://bl…...

nvm安装和切换node版本
1、nvm list查看已安装的node版本 2、查看当前使用的npm和node版本 3、安装某版本的node 4、 切换node版本...
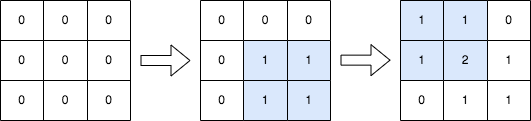
每日一题8.2 2536
2536. 子矩阵元素加 1 给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。 另给你一个二维整数数组 query 。针对每个查询 query[i] [row1i, col1i, row2i, col2i] ,请你执行下述操作:…...
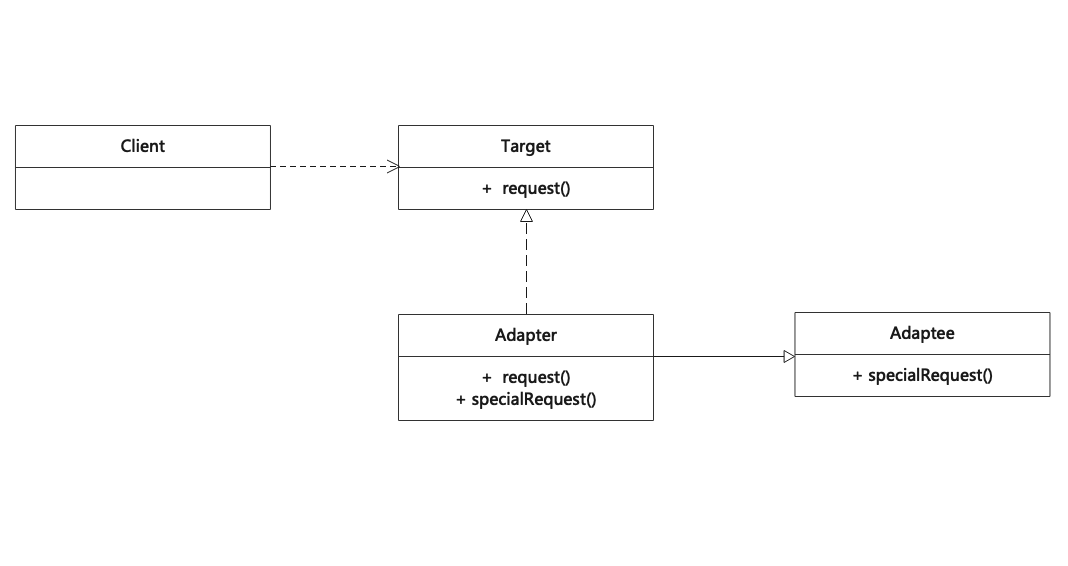
适配器模式(Adapter)
适配器模式用于将一个接口转换成用户希望的另一个接口,适配器模式使接口不兼容的那些类可以一起工作,其别名为包装器(Wrapper)。适配器模式既可以作为类结构型模式,也可以作为对象结构型模式。 Adapter is a structural design pattern that…...

Spring学习笔记——1
Spring学习笔记——1 一、Spring入门1.1、学习路线1.2、传统Javaweb开发困惑及解决方法1.3、三种思想的提出和框架概念1.3.1、IoC、DI和AOP思想提出1.3.2、框架的基本特点 1.4、Spring概述1.5、BeanFactory快速入门1.6、ApplicationContext快速入门1.7、BeanFactory与Applicati…...
leetcode 406. 根据身高重建队列
2023.8.2 这题一开始有点让人懵逼的是有两个维度,一个是身高,还一个是前面人高于自己的人数。这种题一般需要先固定一个维度,再去确定另外一个维度,不要想着兼顾。 经过纸上模拟,我的思路是先通过身高进行从大到小排序…...

Matlab实现AGNES算法
在数据分析和机器学习中,聚类是一种常用的无监督学习方法,它可以将数据点按照某种相似度标准进行分组,从而发现数据中的结构和模式。聚类算法有很多种,其中一种比较经典的是AGNES算法,它是一种基于层次的聚类算法&…...
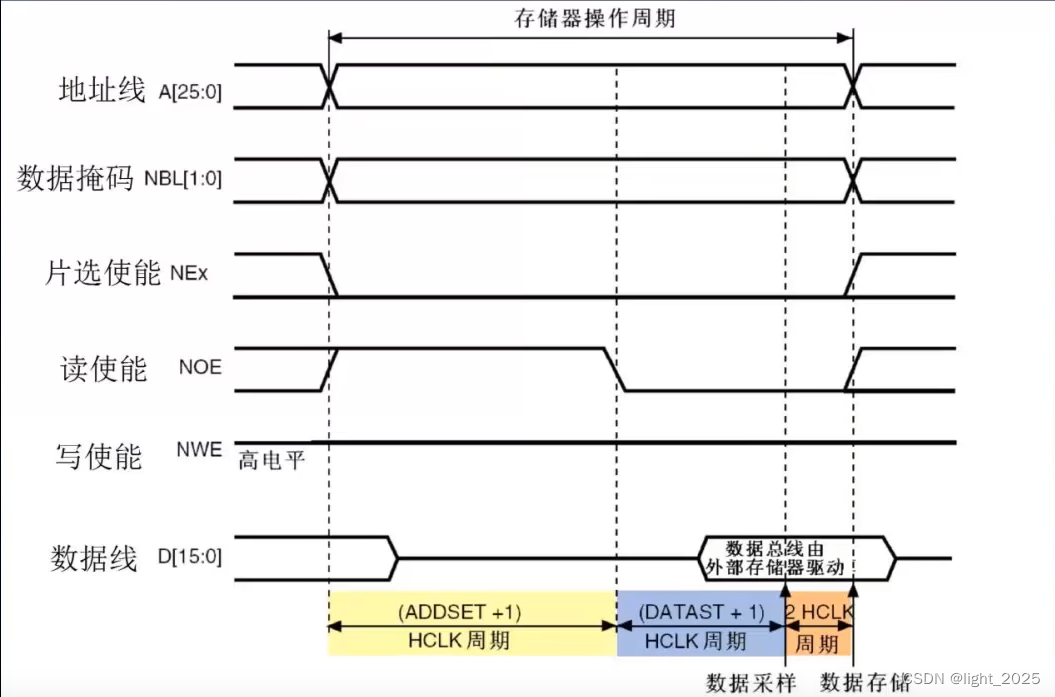
STM32F4_外部SRAM
目录 前言 1. SRAM控制原理 1.1 SRAM功能框图 1.2 SRAM读写时序 2. FSMC简介 2.1 FSMC架构 2.2 FSMC地址映射 2.3 FSMC控制SRAM时序 3. FSMC结构体 4. 库函数配置FSMC 5. 实验程序 5.1 main.c 5.2 SRAM.c 5.3 SRAM.h 前言 STM32F4自带了192K字节的SRAM࿱…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
