【算法提高:动态规划】1.5 状态压缩DP TODO
文章目录
- 状态压缩DP
- 例题列表
- 棋盘式
- 1064. 小国王⭐🐂(好题!)
- 做题套路总结
- 327. 玉米田(好题!🐂 和1064. 小国王差不多的题目)
- 292. 炮兵阵地(和上面两道题差不多,需要多考虑上上一行)
- 集合
- 524. 愤怒的小鸟🚹🚹🚹(TODO)
- 529. 宝藏🚹🚹🚹🚹🚹(TODO)
- 相关链接
状态压缩DP
状压 DP 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。
更多介绍可见:相关链接 部分。
例题列表
棋盘式
1064. 小国王⭐🐂(好题!)
https://www.acwing.com/activity/content/problem/content/1292/
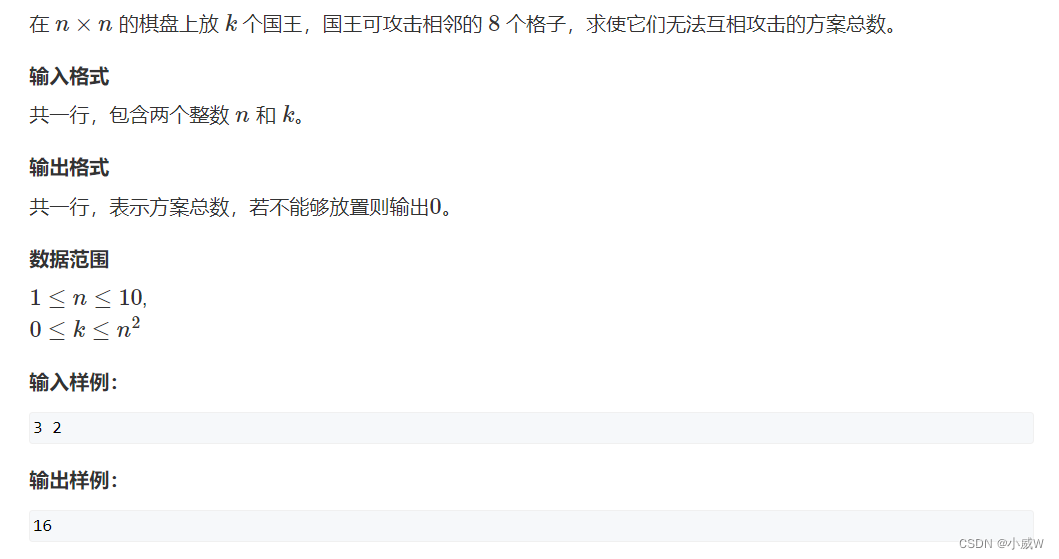
洛谷相同题目链接:P1896 [SCOI2005] 互不侵犯
每个国王会攻击周围一圈儿。
每一层只需要考虑上一层的状态就可以了。
dp数组定义:long[][][] dp = new long[N][K][M]; 第i行,已经放了j个国王,当前行的国王集合为a,此时的方案数。
枚举顺序见代码。
import java.io.BufferedInputStream;
import java.util.*;public class Main {final static int N = 12, M = 1 << 10, K = 110; // 可以开大一点无所谓static int n, m;static List<Integer> state = new ArrayList<>(); // 里面存放的是在一行中没有冲突的集合static int[] cnt = new int[M];static List<Integer>[] head = new ArrayList[M]; // 里面存放的是每一种状态相邻的行可以放置哪些状态static long[][][] dp = new long[N][K][M];static {Arrays.setAll(head, e -> new ArrayList<>());}public static void main(String[] args) {Scanner sin = new Scanner(new BufferedInputStream(System.in));n = sin.nextInt();m = sin.nextInt();// 预先处理出所有可选的状态集合(即在一行内没有冲突的集合),以及这种状态的行中有几个国王for (int i = 0; i < 1 << n; ++i) {if (check(i)) {state.add(i);cnt[i] = count(i);}}// 预先处理每一行之后 相邻的行可以放置哪种状态集合for (int i = 0; i < state.size(); ++i) {for (int j = 0; j < state.size(); ++j) {int a = state.get(i), b = state.get(j);// 如果没有冲突// 没有列上一样的,也没有列上相邻的if ((a & b) == 0 && check(a | b)) {head[i].add(j);}}}// 第i行,已经放了j个国王,当前行的国王集合为adp[0][0][0] = 1;// 枚举每一行for (int i = 1; i <= n + 1; i++) {// 枚举已经选了m个国王(需要从0枚举到m)for (int j = 0; j <= m; ++j) {// 枚举每一种状态作为当前行(不管是不是合法的,无所谓,因为不合法的对应的head[a]里面是空的)for (int a = 0; a < state.size(); ++a) {// 枚举a后面可以跟着的每一种bfor (int b: head[a]) {int c = cnt[state.get(a)];// 如果当前已经选择的国王数量>=当前行的国王数量if (j >= c) {dp[i][j][a] += dp[i - 1][j - c][b];}}}}}System.out.println(dp[n + 1][m][0]);}// 检查一个状态集合是否在这一行内有冲突static boolean check(int state) {for (int i = 0; i < n; ++i) {// 如果连续两列都为1,表示有冲突if (((state >> i & 1) == 1 && (state >> i + 1 & 1) == 1)) return false;}return true;}// 计算这个状态集合中,摆放了几个国王static int count(int state) {int res = 0;for (int i = 0; i < n; ++i) res += state >> i & 1;return res;}
}
做题套路总结
最后来总结一下写法:
- 先预先处理出,所有在一行中没有冲突的列集合
- 然后对计算出对所有合理列集合 来说 没有冲突的列集合
- 最后 枚举行、当前行的列状态、上一行的列状态,计算状态转移
327. 玉米田(好题!🐂 和1064. 小国王差不多的题目)
https://www.acwing.com/problem/content/329/
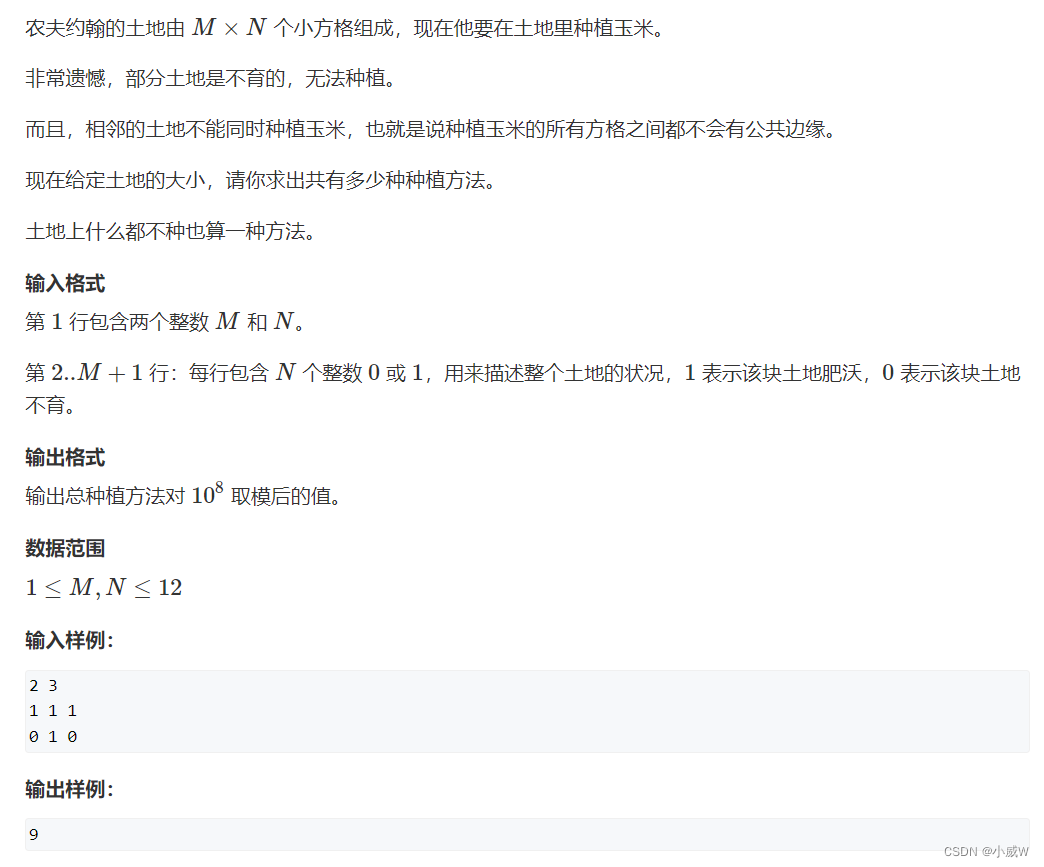
跟上一题相比有一些变化:
- 冲突的范围从周围一圈变成十字的形状
- 部分格子是无法放置玉米的
- 种植玉米的数量是没有限制的
import java.io.BufferedInputStream;
import java.util.*;public class Main {final static int N = 14;final static long MOD = (long)1e8;static int m, n;static int[] land = new int[N]; // 记录每一行中的哪些列是不能种植的static List<Integer> states = new ArrayList<>(); // 记录所有在一行中合法的状态static List<Integer>[] head = new ArrayList[1 << N];static {Arrays.setAll(head, e -> new ArrayList<>());}public static void main(String[] args) {Scanner sin = new Scanner(new BufferedInputStream(System.in));m = sin.nextInt();n = sin.nextInt();for (int i = 1; i <= m; ++i) {for (int j = 0; j < n; ++j) {int t = sin.nextInt();land[i] += (t ^ 1) << j; // 0表示不育}}// 预先处理出在一行中合法的所有状态,加入states中for (int i = 0; i < 1 << n; ++i) {if (check(i)) states.add(i);}// 预先处理出哪两种行可以放在一起for (int i = 0; i < states.size(); ++i) {for (int j = 0; j < states.size(); ++j) {int a = states.get(i), b = states.get(j);// 只要这两行在列上没有重复,就可以放在一起if ((a & b) == 0) {head[i].add(j);}}}long[][] dp = new long[m + 2][states.size() + 1];dp[0][0] = 1; // dp数组初始化// 枚举每一行for (int i = 1; i <= m + 1; ++i) {// 枚举该行的状态for (int j = 0; j < states.size(); ++j) {if ((states.get(j) & land[i]) == 0) {// 枚举可以从这种行转移过来的行for (int k: head[j]) {dp[i][j] = (dp[i][j] + dp[i - 1][k]) % MOD;}}}}System.out.println(dp[m + 1][0]);}static boolean check(int state) {for (int i = 0; i < n - 1; ++i) {// 检查是否有连续两位都是1的情况if ((state >> i & 1) == 1 && ((state >> i + 1 & 1) == 1)) return false;}return true;}
}
Q:为什么 dp[][] 数组初始化时只 设置 dp[0][0] = 1,而不把 所有 dp[0][j] = 1?
A:dp[0][0] = 1表示在还没有种植任何玉米的状态下(也就是前0行),这种情况只有1种。而dp[0][j] (j != 0)的含义是,在还没有种植任何玉米的状态下,最后一行(也就是不存在的这一行)的种植状态是states[j]的种植方式数量,这显然是不可能的,所以dp[0][j] (j != 0)都应该为0。
292. 炮兵阵地(和上面两道题差不多,需要多考虑上上一行)
https://www.acwing.com/problem/content/294/

跟上面两道题目相比,多考虑上上一行就好了。
dp 递推的过程也 多写一层循环。
import java.io.BufferedInputStream;
import java.util.*;public class Main {final static int N = 105, M = 11;static int n, m;static int[] land = new int[N], cnt = new int[1 << M]; // 记录每一行,不能放置炮兵的列集合static List<Integer> states = new ArrayList<>(); // 记录所有在一行中合理的列集合static List<Integer>[] head = new ArrayList[1 << M];static {Arrays.setAll(head, e -> new ArrayList<>());}public static void main(String[] args) {Scanner sin = new Scanner(new BufferedInputStream(System.in));n = sin.nextInt();m = sin.nextInt();// 记录每一行不能被放置的列集合for (int i = 1; i <= n; ++i) {String s = sin.next();for (int j = 0; j < m; ++j) {land[i] += (s.charAt(j) == 'H'? 1: 0) << j;}}// 计算出所有在一行中合理的列集合for (int j = 0; j < 1 << m; ++j) {if (check(j)) {states.add(j);cnt[j] = count(j);}}// 计算出各个集合可以和哪些集合相邻int l = states.size();for (int i = 0; i < l; ++i) {for (int j = 0; j < l; ++j) {if ((states.get(i) & states.get(j)) == 0) {head[i].add(j);}}}int[][][] dp = new int[n + 1][l][l];// 枚举每一行for (int r = 1; r <= n; ++r) {// 枚举当前的每个集合for (int i = 0; i < l; ++i) {if ((states.get(i) & land[r]) == 0) {// 枚举上一个集合for (int j: head[i]) {// 枚举上上个集合for (int k: head[j]) {if ((states.get(i) & states.get(k)) == 0) {dp[r][j][i] = Math.max(dp[r - 1][k][j] + cnt[states.get(i)], dp[r][j][i]);}}}}}}int ans = 0;for (int i = 0; i < l; ++i) {for (int j = 0; j < l; ++j) {ans = Math.max(ans, dp[n][i][j]);}}System.out.println(ans);}private static boolean check(int state) {for (int i = 0; i < m; ++i) { // 这里最好写成 i < m,写成 i < m - 2 时答案就不对了// 邻近两个范围内不能有炮兵if ((state >> i & 1) == 1 && ((state >> i + 1 & 1) == 1 || (state >> i + 2 & 1) == 1)) return false;}return true;}// 计算这种集合中有多少个炮兵static int count(int state) {int res = 0;for (int i = 0; i < m; ++i) res += state >> i & 1;return res;}
}
集合
524. 愤怒的小鸟🚹🚹🚹(TODO)
https://www.acwing.com/problem/content/526/


数据范围:
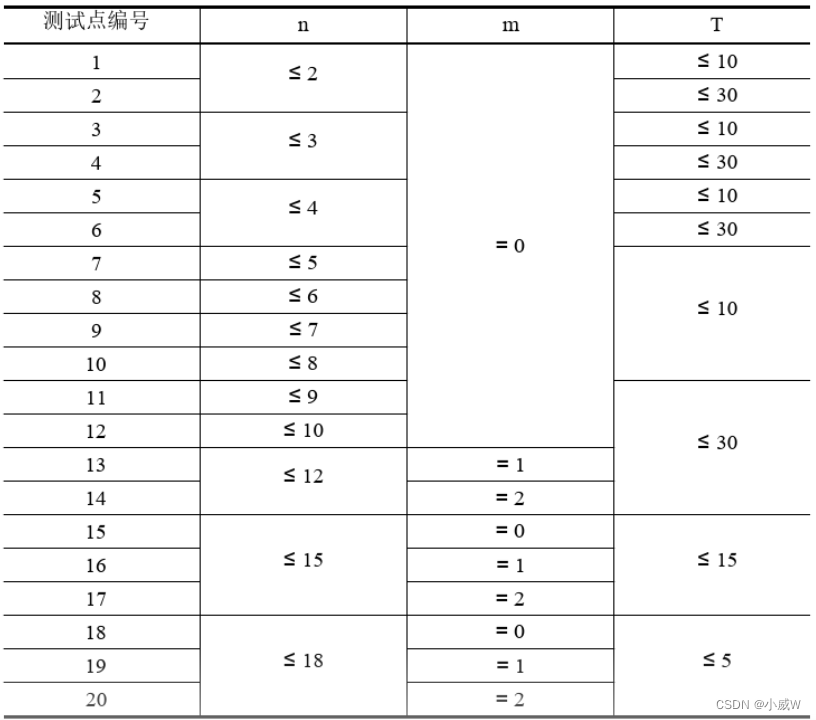
在这里插入代码片
529. 宝藏🚹🚹🚹🚹🚹(TODO)
https://www.acwing.com/problem/content/531/

在这里插入代码片
相关链接
从集合论到位运算——常见位运算技巧及相关习题 & 状态压缩DP
【力扣周赛】第 355 场周赛(构造&二分答案&异或前缀 状态压缩⭐)
【算法基础:动态规划】5.4 状态压缩DP
相关文章:

【算法提高:动态规划】1.5 状态压缩DP TODO
文章目录 状态压缩DP例题列表棋盘式1064. 小国王⭐🐂(好题!)做题套路总结 327. 玉米田(好题!🐂 和1064. 小国王差不多的题目)292. 炮兵阵地(和上面两道题差不多ÿ…...
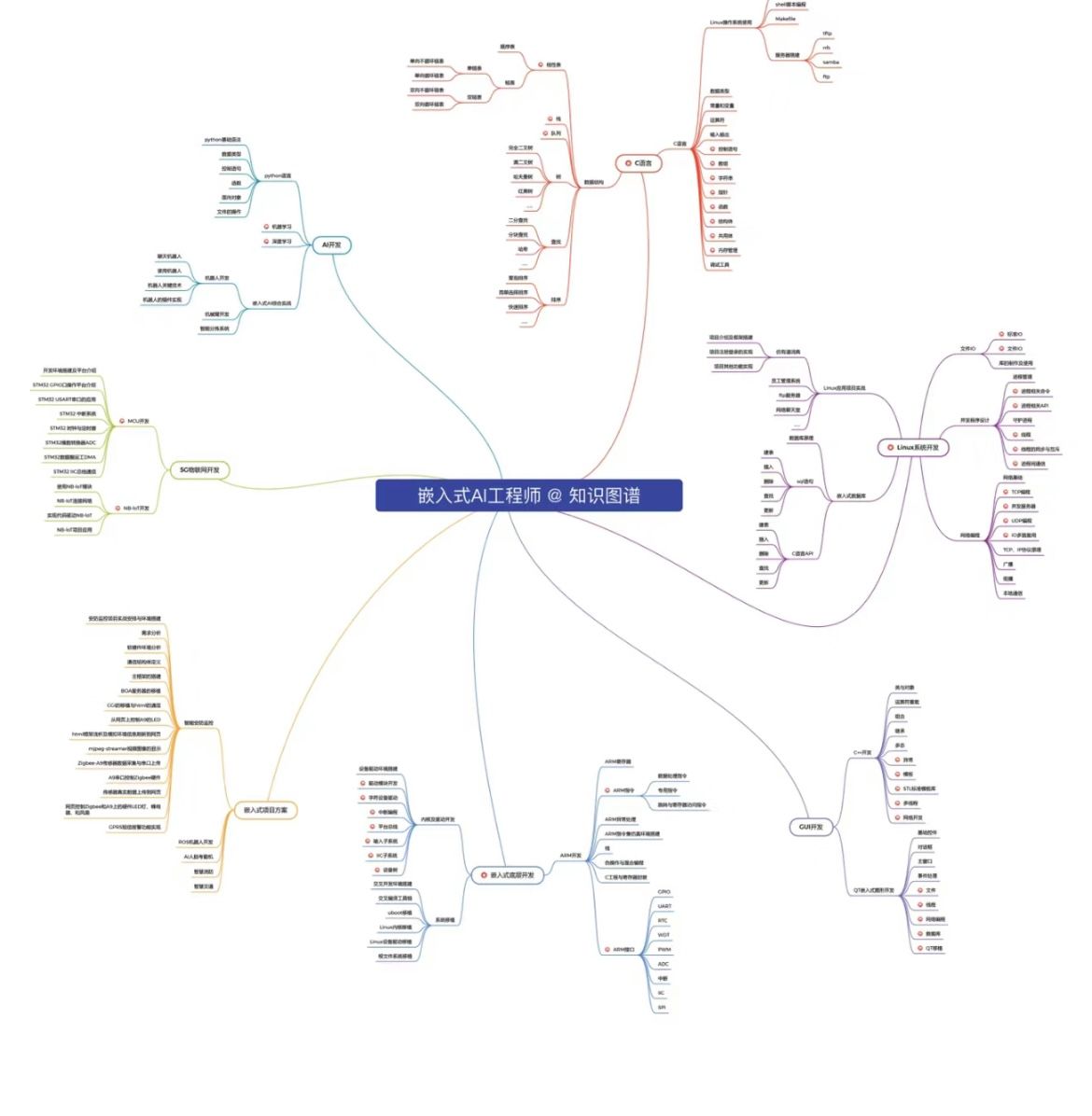
建网站一般使用Windows还是liunx好?
建网站一般使用Windows还是liunx好? 1;服务器配置比较低时,最好使用linux系统。 对于一个电脑新手,刚开始做网站时,都会选择入门级的服务器,我刚开始做网站时,就是这样的。我购买了一台入门级服…...
NodeJs后端项目使用docker打包部署
docker安装看之前的文章 默认已经安装好docker并且配置没有问题 拉取项目 https://gitee.com/coder-msc/docker-node 本地跑一个看看 pnpm install pnpm start 本地访问 http://localhost:1301/getname?name%E5%93%88%E5%88%A9%E6%B3%A2%E7%89%B9项目整个上传服务器 查看…...

ARM单片机中断处理过程解析
前言 中断,在单片机开发中再常见不过了。当然对于中断的原理和执行流程都了然于胸,那么对于ARM单片机中断的具体处理行为,你真的搞清楚了吗? 今天来简单聊一聊,ARM单片机中断处理过程中的具体行为是什么样的…...

关于SEDEX会员与平台的相关问题汇总
【关于SEDEX会员与平台的相关问题汇总】 01.会员资格有效期是多久? Sedex会员资格有效期为12个月,您也可以选择更长期的会员资格。您支付会员年费时,在“订阅信息”框下的“延长订阅期限”中输入年数,即可获得更长的会员资格时效。…...
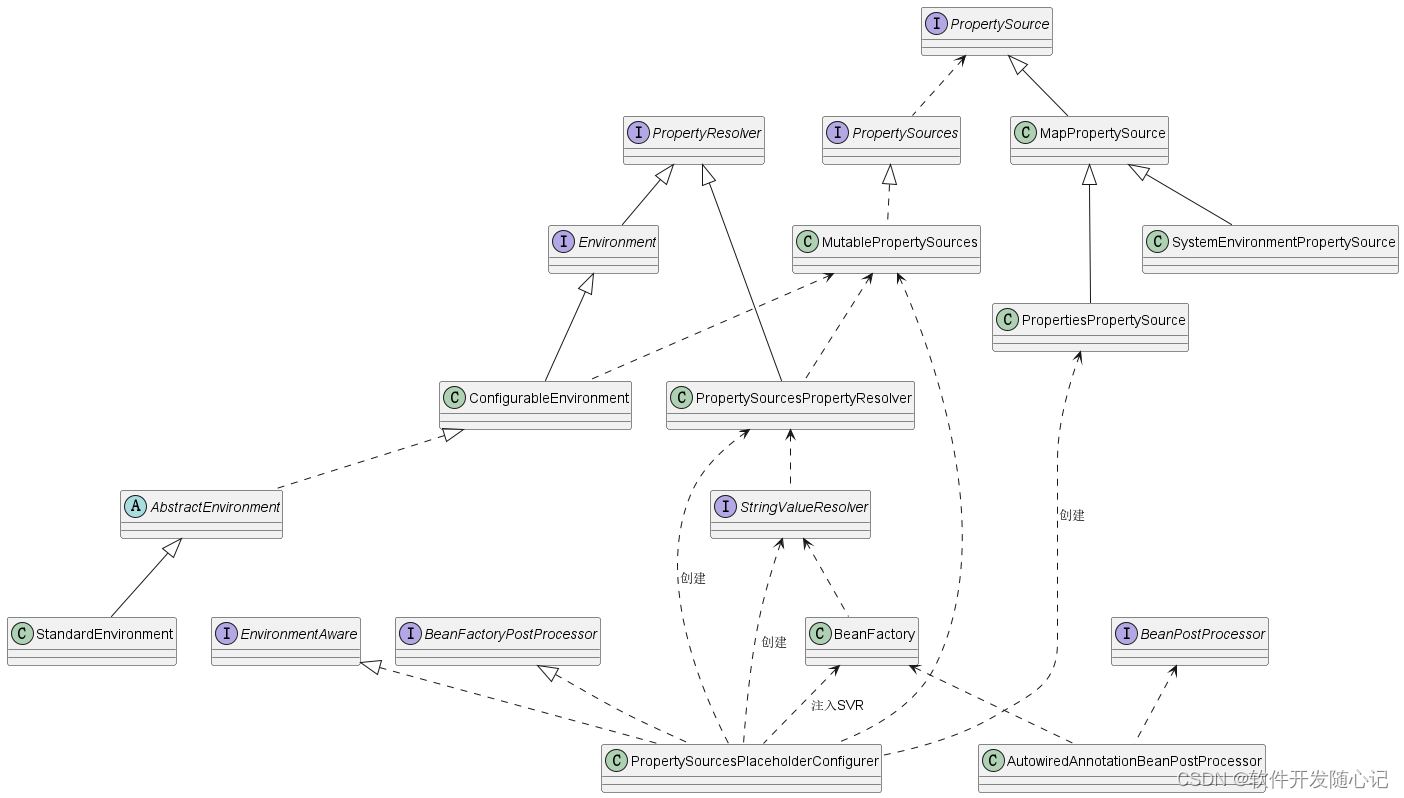
解读Spring-context的property-placeholder
在spring中,如果要给程序定义一些参数,可以放在application.properties中,通过<context:property-placeholder>加载这个属性文件,然后就可以通过value给我们的变量自动赋值,如果你们的程序可能运行在多个环境中&…...
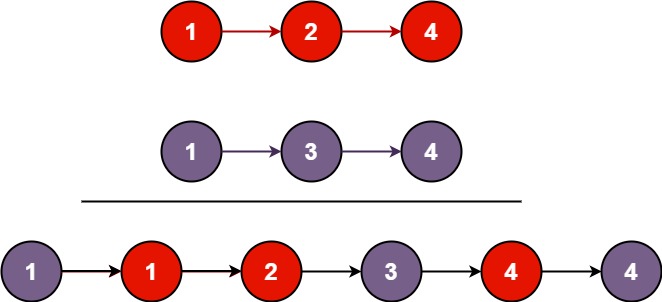
【Rust】枚举类型创建单链表以及常见的链表操作方法
目录 单链表 用枚举表达链表 枚举enum Box容器 创建节点 1. 创建并打印 2. match 匹配 3. 节点初始化 4.节点嵌套 追加节点 1. 尾插法 2. 链表追加方法 3. 头插法 4. 改写成单链表方法 遍历链表 1. 递归法 2. 递推法 3. 改写成单链表方法 自定义Display tr…...

Excel 两列数据中相同的数据进行同行显示
一、要求 假设您有两个列,分别是A列和B列,需要在C列中找出A列对应的B列的值。 二、方案 方法1:寻常思路 凸显重复项对A列单独进行筛选–按颜色进行排序,然后升序对B列重复上述操作即可 方法2:两个公式 VLOOKUP 纵向查找…...
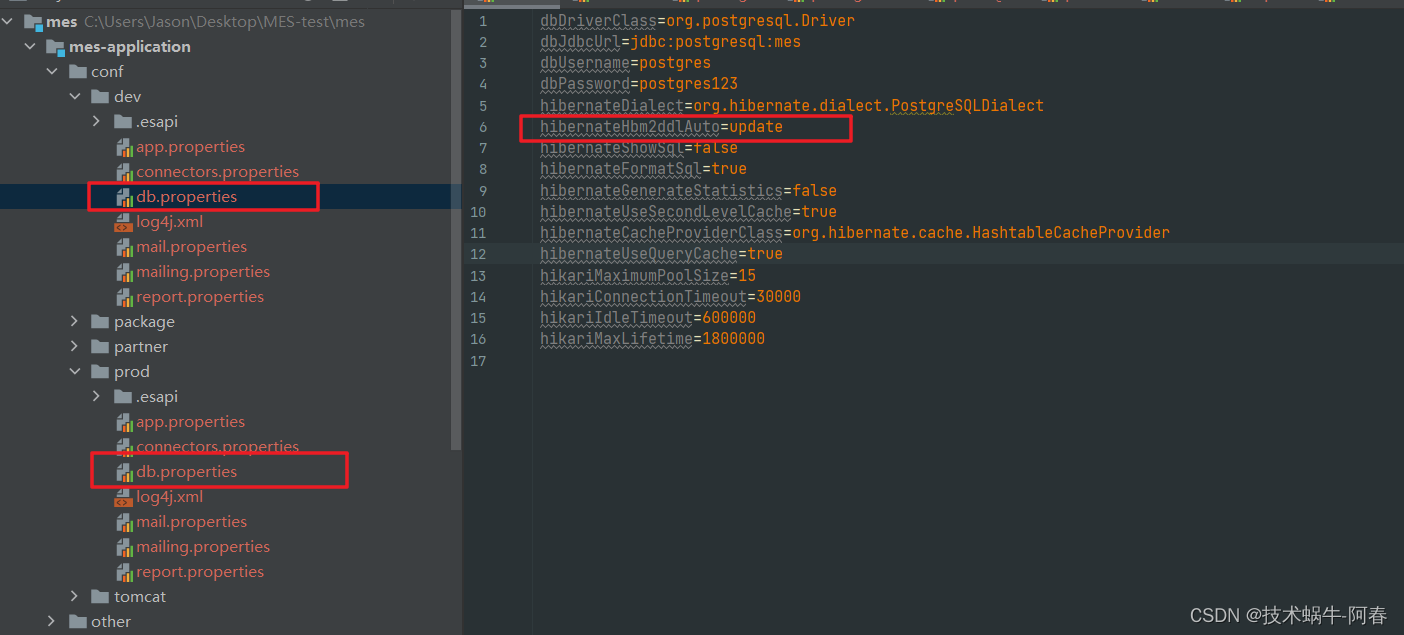
Windows本地安装配置Qcadoo MES系统
简介 Qcadoo MES是一款功能强大且灵活的开源MES(制造执行系统),旨在为制造业务提供全面的管理和监控解决方案。本篇博客将教您如何在Windows操作系统上安装和配置Qcadoo MES系统,以便您能够轻松管理和监控制造过程。 环境要求 …...

涛思数据与拾贝云达成战略合作,携手赋能工业数字化转型
2023 年 7 月 27 日,北京涛思数据科技有限公司(以下简称“涛思数据”)与广州拾贝云科技有限公司(以下简称“拾贝云”)于广州签署战略合作协议。双方围绕电力行业的需求与痛点展开积极讨论,就如何量身打造最…...

nginx 配置多域名多站点 Ubuntu
nginx 配置多域名多站点 Ubuntu 一、安装 nginx apt install nginx二、配置文件说明 nginx 的配置文件在 /etc/nginx 目录下,它的默认内容是这样的 root2bd0:/etc/nginx# ll total 72 drwxr-xr-x 8 root root 4096 Jul 31 15:21 ./ drwxr-xr-x 104 root root …...
)
Docker实践:使用Docker搭建个人开发环境(极简版)
文章目录 说明教程1. 编写 Dockerfile2. 编写 docker-compose.yml3. 使用容器创建容器启动容器进入容器命令行VSCode 4. 关闭容器5. 备份容器导出导入 6. 重置容器 相关资料文章合集详细了解本文在个人电脑上安装 Docker容器使用 NVIDIA 显卡托管镜像运行GUI程序 说明 本文是在…...

SQL从三个表中根据时间分别查询并汇总数量一行展示
需求:如果您要从三个表中根据时间分别查询并汇总数量,然后将结果以时间和数量一行展示,可以使用子查询和条件聚合。 入库主表 入库明细表 出库主表 出库明细表 退货主表 退货明细表 SQL代码 SELECT time,sum(a.inQty) as inQty,sum(a.outQty…...

同样是跨端框架,React会不会被VUE取代?
看到知乎上有比较多的类似问题,正好这两个框架在以往的一些项目中都有实践过,就借着本篇文章说说我个人的看法。 先摆个结论:不会,毕竟各有千秋,除非跨端框架有被更好的概念所替代,又或者App已经彻底过气了…...
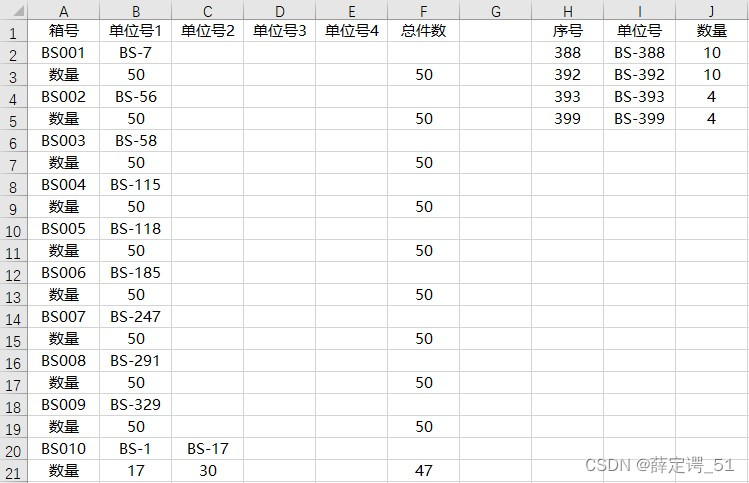
Excel·VBA定量装箱、凑数值金额、组合求和问题
如图:对图中A-C列数据,根据C列数量按照一定的取值范围,组成一个分组装箱,要求如下: 1,每箱数量最好凑足50,否则为47-56之间; 2,图中每行数据不得拆分; 3&…...

通过Jmeter压测存储过程
目录 一、存储过程准备: 二、测试工具准备: 三、工具配置及执行: 1、配置JDBC Connection Configuration: 2、配置吞吐量控制器(可跳过): 3、配置JDBC Request: 对于存储过程…...

Spring笔记之Spring对IoC的实现
文章目录 IoC控制反转依赖注入set注入注入外部Bean注入内部Bean注入简单类型通过注入方式实现javax.sql.DateSource接口测试简单类型 级联属性赋值(了解)注入数组注入List集合注入Set集合注入Map集合注入Properties注入null和空字符串不给属性赋值使用 注…...
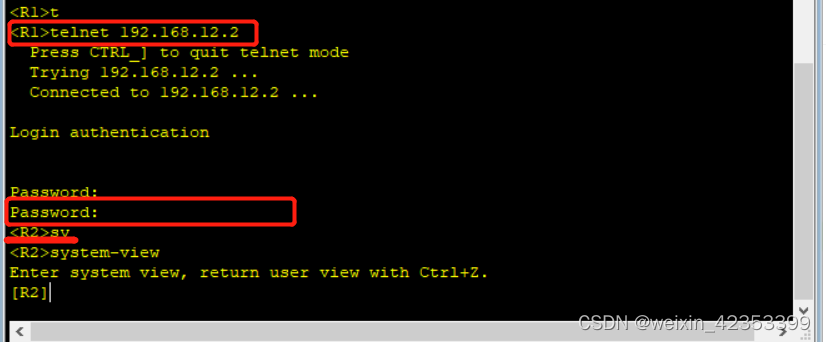
【eNSP】Telnet远程登录
Telnet远程登录 eNSP软件TelnetTelnet远程登录-路由连接关闭防火墙eNSP根据图1画图路线配置路由端口IP配置路由R1改名配置接口IP 配置路由R2 配置R2的远程登录设置登录用户授权级别退出登录超时时间 Telnet测试 eNSP软件 eNSP(Enterprise Network Simulation Platform)是一款由…...

SOP/详解*和**/python数据结构(iter,list,tuple,dict)/ 解包
一、错误解决合集 1. > combined_seq.named_children() 2. isinstance 2th parameter : must be a type or tuple of types > 改为tuple,不要用列表。改为 LLLayer (nn.Conv2d,nn.Linear) 3. File “test.py”, line 90, in calculate_fin_fout print(“hi”…...

使用webdriver-manager解决浏览器与驱动不匹配所带来自动化无法执行的问题
1、前言 在我们使用 Selenium 进行 UI 自动化测试时,常常会因为浏览器驱动与浏览器版本不匹配,而导致自动化测试无法执行,需要手动去下载对应的驱动版本,并替换原有的驱动,可能还会遇到跨操作系统进行测试的时候&…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
