P3373 【模板】线段树 2(乘法与加法)(内附封面)
【模板】线段树 2
题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 x x x;
- 将某区间每一个数加上 x x x;
- 求出某区间每一个数的和。
输入格式
第一行包含三个整数 n , q , m n,q,m n,q,m,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 q q q 行每行包含若干个整数,表示一个操作,具体如下:
操作 1 1 1: 格式:1 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数乘上 k k k
操作 2 2 2: 格式:2 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数加上 k k k
操作 3 3 3: 格式:3 x y 含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和对 m m m 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 3 3 3 的结果。
样例 #1
样例输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
样例输出 #1
17
2
提示
【数据范围】
对于 30 % 30\% 30% 的数据: n ≤ 8 n \le 8 n≤8, q ≤ 10 q \le 10 q≤10。
对于 70 % 70\% 70% 的数据:$n \le 10^3 , , ,q \le 10^4$。
对于 100 % 100\% 100% 的数据: 1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105, 1 ≤ q ≤ 1 0 5 1 \le q \le 10^5 1≤q≤105。
除样例外, m = 571373 m = 571373 m=571373。
(数据已经过加强 _)
样例说明:

故输出应为 17 17 17、 2 2 2( 40 m o d 38 = 2 40 \bmod 38 = 2 40mod38=2)。
大致思路
线段树模板,不过多解释,
首先,线段树是二叉树,因此具有二叉树的性质,其左儿子节点与右儿子节点是固定的,具体实现如下,其中, l c ( x ) lc(x) lc(x)为左儿子, r c ( x ) rc(x) rc(x)为右儿子(对应2n与2+1)
#define lc(x) (x<<1)
#define rc(x) ((x<<1)|1)
其次,线段树的建立为递归建立,最底层的节点对应的就是 a [ 1... n ] a[1...n] a[1...n]
void build(int x,int l,int r){tag_add[x]=0;tag_mul[x]=1;if(l==r){sm[x]=a[l];return;}int mid=(l+r)>>1;build(lc(x),l,mid);build(rc(x),mid+1,r);pushup(x);return;
}
s m [ x ] = s m [ l c ( x ) ] + s m [ r c ( x ) ] sm[x]=sm[lc(x)]+sm[rc(x)] sm[x]=sm[lc(x)]+sm[rc(x)]通常会被单独写做一个函数pushup
void pushup(int x){sm[x]=(sm[lc(x)]+sm[rc(x)])%mod;
}
区间修改与查询
单点修改与查询只需如同建树一样查找到节点修改并pushup或return即可,不过多赘述。
对于区间修改,我们需要用到 lazy_tag 对于一次修改操作我们先不全部进行修改,当火烧眉毛不得不用到这个值时再进行修改,对于一种运算使用一个tag[]数组实现。
此模板题有两种运算,因此用 tag_add 与 tag_mul 分别记录
int sm[N<<2],a[N<<2],tag_add[N<<2],tag_mul[N<<2];
-
cover
- 两种运算,我们先乘后加
- 对于乘法,节点 x 对应的 sm[x] 就是一段区间的和,根据乘法分配律,我们直接 s m [ x ] ∗ m u l sm[x]*mul sm[x]∗mul 即可,同样, tag_add也要乘mul,已有的 tag_mul 根据乘法结合律,直接 t a g . m u l [ x ] ∗ m u l tag.mul [ x ] * mul tag.mul[x]∗mul,记得最后取模
void cover(int x,int l,int r,int ad,int mul){sm[x]=sm[x]*mul%mod;sm[x]+=(r-l+1)*ad%mod;sm[x]%=mod;tag_mul[x]*=mul;tag_mul[x]%=mod;tag_add[x]*=mul;tag_add[x]+=ad;tag_add[x]%=mod;
}
void pushdown(int x,int l,int r){int mid=(l+r)>>1;cover(lc(x),l,mid,tag_add[x],tag_mul[x]);cover(rc(x),mid+1,r,tag_add[x],tag_mul[x]);tag_add[x]=0;tag_mul[x]=1;
}
void update(int x,int l,int r,int L,int R,int ad,int mul){
// if(r<L||l>R)return;if(l>=L&&R>=r){cover(x,l,r,ad,mul);//若已被完全包含,进行一次计算return;}pushdown(x,l,r);//注意下传tagint mid=(l+r)>>1;if(L<=mid)update(lc(x),l,mid,L,R,ad,mul);//下传左儿子if(R>mid) update(rc(x),mid+1,r,L,R,ad,mul);//下传右儿子
// update(lc(x),l,mid,L,R,ad,mul);
// update(rc(x),mid+1,r,L,R,ad,mul);pushup(x);
}
-
query
-
关键部分
- 实现区间询问,原理基本与 update 一致,注意区间被完全包含后返回值与取模。
- 同样给出三种写法,将注释掉的内容解开并将 if (L<=mid)…两行注释即为第二种写法
int query(int x,int l,int r,int L,int R){
// if(r<L||l>R)return 0;int res=0;if(l>=L&&R>=r){return sm[x];}pushdown(x,l,r);int mid=(l+r)>>1;if(L<=mid)res+=(query(lc(x),l,mid,L,R)%mod);if(R>mid) res+=(query(rc(x),mid+1,r,L,R)%mod);
// res+=(query(lc(x),l,mid,L,R)%mod);
// res+=(query(rc(x),mid+1,r,L,R)%mod);return res%mod;
}
int query(int x,int l,int r,int L,int R){if(r<L||l>R)return 0;if(l>=L&&R>=r){return sm[x];}pushdown(x,l,r);int mid=(l+r)>>1;return (query(lc(x),l,mid,L,R)+query(rc(x),mid+1,r,L,R))%mod;
}
真的快被线段树ex吐了
AC CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long int
const int N=1e6+2233;
#define lc(x) (x<<1)
#define rc(x) ((x<<1)|1)
int n,m,mod;
int sm[N<<2],a[N<<2],tag_add[N<<2],tag_mul[N<<2];
void pushup(int x){sm[x]=(sm[lc(x)]+sm[rc(x)])%mod;
}
void build(int x,int l,int r){tag_add[x]=0;tag_mul[x]=1;if(l==r){sm[x]=a[l];return;}int mid=(l+r)>>1;build(lc(x),l,mid);build(rc(x),mid+1,r);pushup(x);return;
}
void cover(int x,int l,int r,int ad,int mul){sm[x]=sm[x]*mul%mod;sm[x]+=(r-l+1)*ad%mod;sm[x]%=mod;tag_mul[x]*=mul;tag_mul[x]%=mod;tag_add[x]*=mul;tag_add[x]+=ad;tag_add[x]%=mod;
}
void pushdown(int x,int l,int r){int mid=(l+r)>>1;cover(lc(x),l,mid,tag_add[x],tag_mul[x]);cover(rc(x),mid+1,r,tag_add[x],tag_mul[x]);tag_add[x]=0;tag_mul[x]=1;
}
void update(int x,int l,int r,int L,int R,int ad,int mul){
// if(r<L||l>R)return;if(l>=L&&R>=r){cover(x,l,r,ad,mul);return;}pushdown(x,l,r);int mid=(l+r)>>1;if(L<=mid)update(lc(x),l,mid,L,R,ad,mul);if(R>mid) update(rc(x),mid+1,r,L,R,ad,mul);
// update(lc(x),l,mid,L,R,ad,mul);
// update(rc(x),mid+1,r,L,R,ad,mul);pushup(x);
}
int query(int x,int l,int r,int L,int R){
// if(r<L||l>R)return 0;int res=0;if(l>=L&&R>=r){return sm[x];}pushdown(x,l,r);int mid=(l+r)>>1;if(L<=mid)res+=(query(lc(x),l,mid,L,R)%mod);if(R>mid) res+=(query(rc(x),mid+1,r,L,R)%mod);
// res+=(query(lc(x),l,mid,L,R)%mod);
// res+=(query(rc(x),mid+1,r,L,R)%mod);return res%mod;
}
signed main(){scanf("%lld %lld %lld",&n,&m,&mod);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}build(1,1,n);while(m--){int op,xx,yy,kk;scanf("%lld",&op);if(op==1){scanf("%lld %lld %lld",&xx,&yy,&kk);update(1,1,n,xx,yy,0,kk);}if(op==2){scanf("%lld %lld %lld",&xx,&yy,&kk);update(1,1,n,xx,yy,kk,1);}if(op==3){scanf("%lld %lld",&xx,&yy);printf("%lld\n",query(1,1,n,xx,yy));}}return 0;
}
附封面(佐仓大法好!)

相关文章:

P3373 【模板】线段树 2(乘法与加法)(内附封面)
【模板】线段树 2 题目描述 如题,已知一个数列,你需要进行下面三种操作: 将某区间每一个数乘上 x x x;将某区间每一个数加上 x x x;求出某区间每一个数的和。 输入格式 第一行包含三个整数 n , q , m n,q,m n,…...
)
实现langchain-ChatGLM API调用客户端(及未解决的问题)
langchain-ChatGLM是一个基于本地知识库的LLM对话库。其基于text2vec-large-Chinese为Embedding模型,ChatGLM-6B为对话大模型。原项目地址:https://github.com/chatchat-space/langchain-ChatGLM 对于如何本地部署ChatGLM模型,可以参考我之前…...

【AltWalker】模型驱动:轻松实现自动化测试用例的生成和组织执行
目录 模型驱动的自动化测试 优势 操作步骤 什么是AltWalker? 安装AltWalker 检查是否安装了正确的版本 牛刀小试 创建一个测试项目 运行测试 运行效果 在线模型编辑器 VScode扩展 本地部署 包含登录、选择产品、支付、退出登录的模型编写 模型效果 1…...

大数据课程E3——Flume的Sink
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Sink的HDFS Sink; ⚪ 掌握Sink的Logger Sink; ⚪ 掌握Sink的File Roll Sink; ⚪ 掌握Sink的Null Sink; ⚪ 掌握Sink的AVRO Sink; ⚪ 掌握Sink的Custom Sink; 一、HDFS Sink …...

如何快速做单元测试?
首先写unit test之前,要确认自己的测试遵循两个原则: 1、尽量不要干涉原来的代码。从阅读代码的体验来说,不要让你的测试(哪怕是一小段if..else...的代码)出现在你准备测试的代码中。 2、代码要只是测试某个class里面…...

不同对象的集合转换
https://blog.csdn.net/qq_42483473/article/details/128984514 import com.alibaba.fastjson.JSON;import java.util.ArrayList; import java.util.List;/*** author */ public class ObjectConversion {/*** 从List<A> copy到List<B>* param list List<B>…...
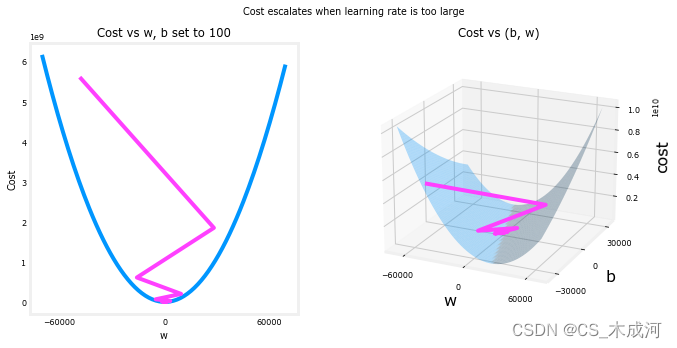
【机器学习】Gradient Descent
Gradient Descent for Linear Regression 1、梯度下降2、梯度下降算法的实现(1) 计算梯度(2) 梯度下降(3) 梯度下降的cost与迭代次数(4) 预测 3、绘图4、学习率 首先导入所需的库: import math, copy import numpy as np import matplotlib.pyplot as plt plt.styl…...

直播读弹幕机器人:直播弹幕采集+文字转语音(附完整代码)
目录 前言代码实现请求数据解析数据文字转语音完整代码 高级点的tk界面版 前言 直播读弹幕机器人是指能够实时读取直播平台上观众发送的弹幕,并将其转化为语音进行播放的机器人。这种机器人通常会使用文字转语音技术,将接收到的弹幕文本转为语音&#x…...

K3s vs K8s:轻量级对决 - 探索替代方案
在当今云原生应用的领域中,Kubernetes(简称K8s)已经成为了无可争议的领导者。然而,随着应用规模的不断增长,一些开发者和运维人员开始感受到了K8s的重量级特性所带来的挑战。为了解决这一问题,一个名为K3s的…...
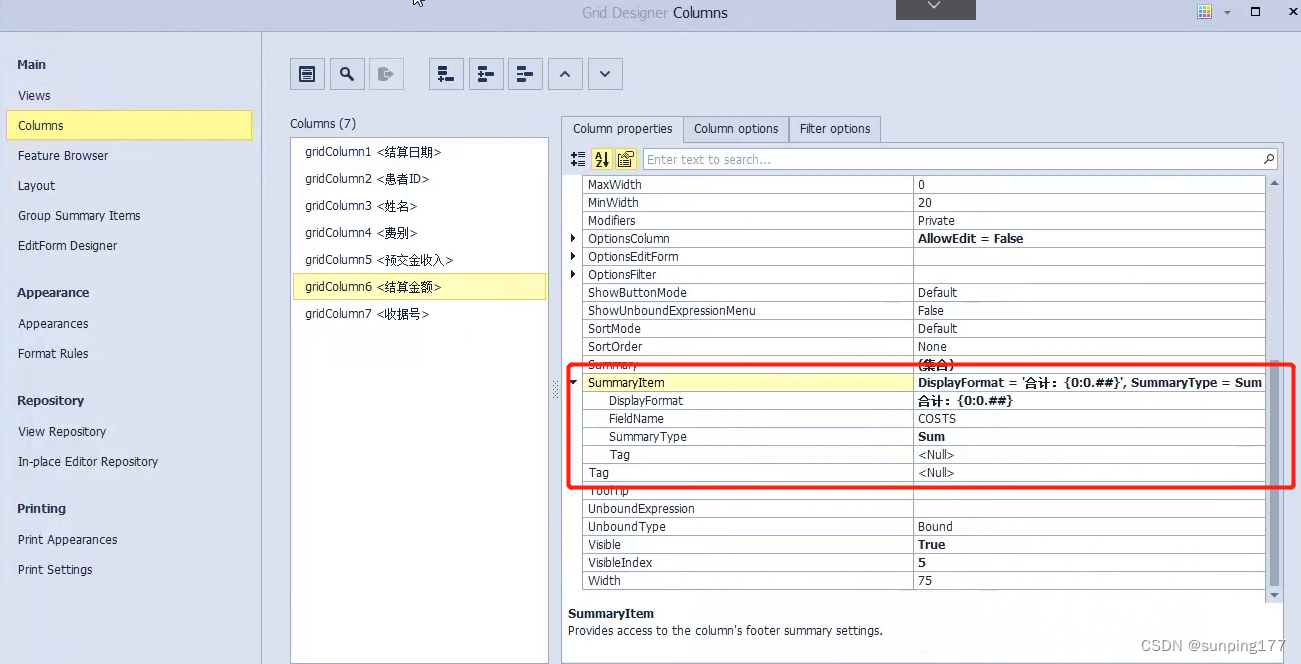
dev控件gridControl,gridview中添加合计
需求:在合并结账查询中,双击每一条结账出现这次结账对应的结算明细: 弹出的页面包括:结算日期,ID,姓名,费别,预交金收入,结算金额,收据号,合计&a…...

SpringBoot基础认识
创建SpringBoot模块 首先需要引设置maven并引用maven环境 1.打开项目结构,new module,选择Spring Initializr,URL选默认: group填写分组如com.kdy , Artifact起个模块名如springboot_quickstart,Type选择M…...
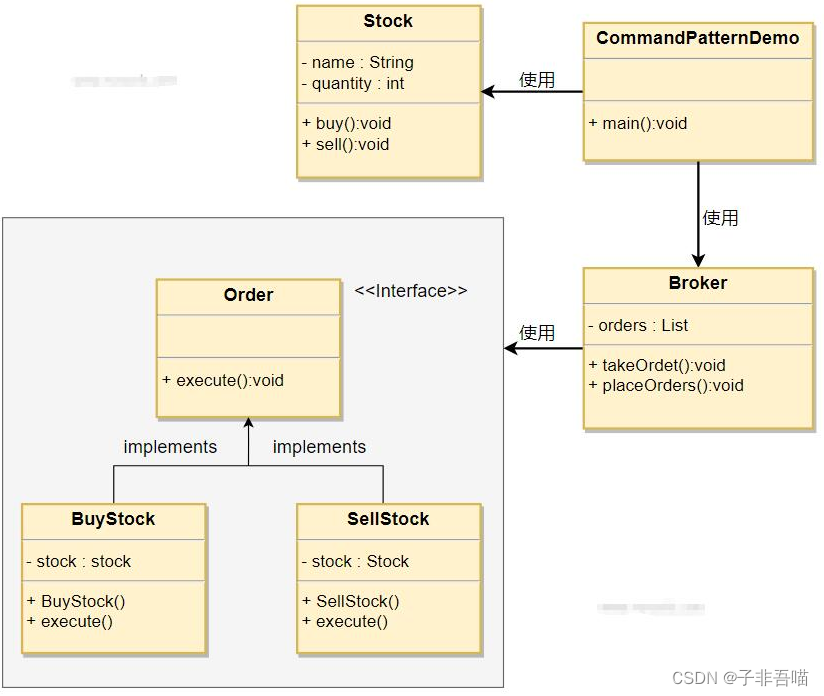
二十三种设计模式第十九篇--命令模式
命令模式是一种行为设计模式,它将请求封装成一个独立的对象,从而允许您以参数化的方式将客户端代码与具体实现解耦。在命令模式中,命令对象充当调用者和接收者之间的中介。这使您能够根据需要将请求排队、记录请求日志、撤销操作等。 命令模…...

STM32基础入门学习笔记:基础知识和理论 开发环境建立
文件目录: 一:基础知识和理论 1.ARM简介 2.STM32简介 3.STM32命名规范 4.STM32内部功能* 5.STM32接口定义 二:开发环境建立 1.开发板简介 2.ISP程序下载 3.最小系统电路 4.KEIL的安装 5.工程简介与调试流程 6.固件库的安装 7.编…...

Qt应用开发(基础篇)——数值微调输入框QAbstractSpinBox、QSpinBox、QDoubleSpinBox
目录 一、前言 二、QAbstractSpinBox类 1、accelerated 2、acceptableInput 3、alignment 4、buttonSymbols 5、correctionMode 6、frame 7、keyboardTracking 8、readOnly 9、showGroupSeparator 10、specialValueText 11、text 12、wrapping 13、信号 二、Q…...

html | 无js二级菜单
1. 效果图 2. 代码 <meta charset"utf-8"><style> .hiddentitle{display:none;}nav ul{list-style-type: none;background-color: #001f3f;overflow:hidden; /* 父标签加这个,防止有浮动子元素时,该标签失去高度*/margin: 0;padd…...
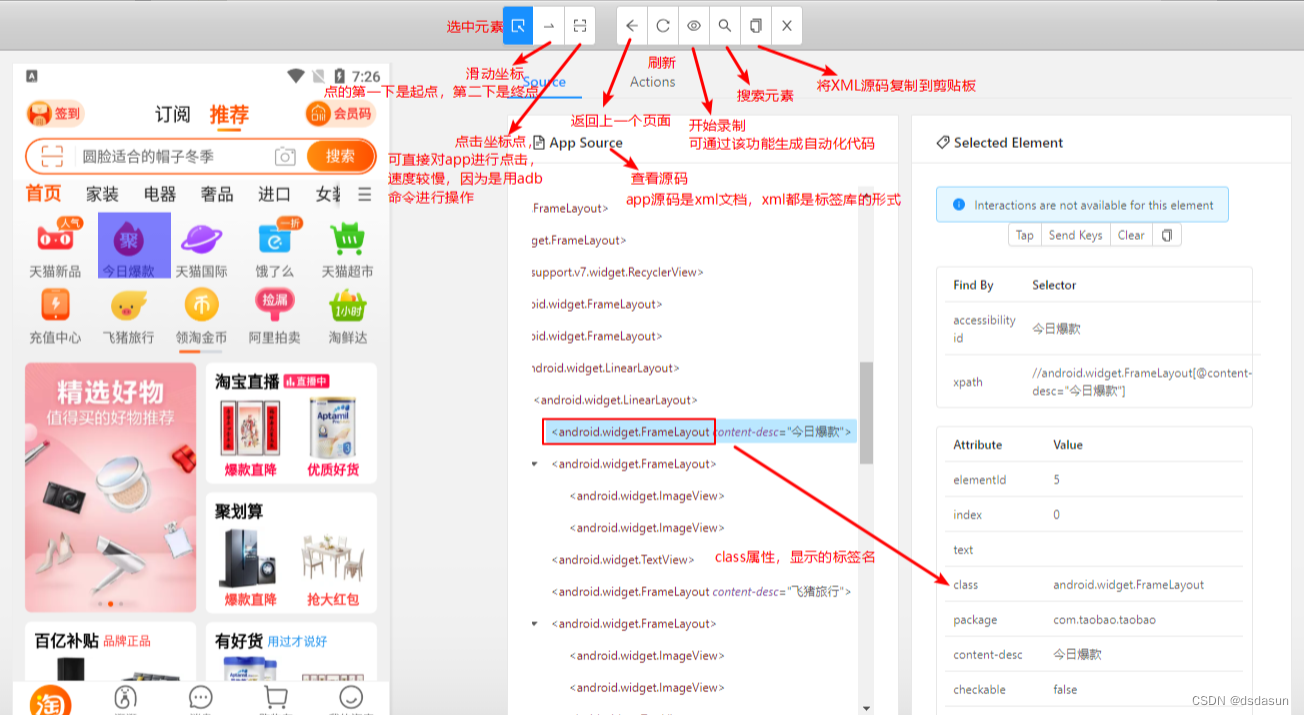
appium的基本使用
appium的基本使用 一、appium的基本使用appium环境安装1、安装Android SDK 2、安装Appium3、安装手机模拟器4、Pycharm安装 appium-python-alicent5、连接appium和模拟器6、Python代码调用appium软件,appium软件在通过adb命令调用android操作系统(模拟器…...
Dockerfile构建nginx镜像(编译安装)
Dockerfile构建nginx镜像 1、建立工作目录 [rootdocker ~]# mkdir nginx [rootdocker ~]# cd nginx/ 2、编写Dockerfile文件 [rootdocker nginx]# vim run.sh [rootdocker nginx]# vim Dockerfile #基于的基础镜像 FROM centos:7#镜像作者信息 MAINTAINER Crushlinux <…...

手机屏幕视窗机器视觉定位软硬件-康耐德
【检测目的】 手机屏幕视窗视觉定位 【效果图片】 【安装示意图】 【硬件配置】...

Databend 开源周报第 104 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 从 Kafka 载入数…...
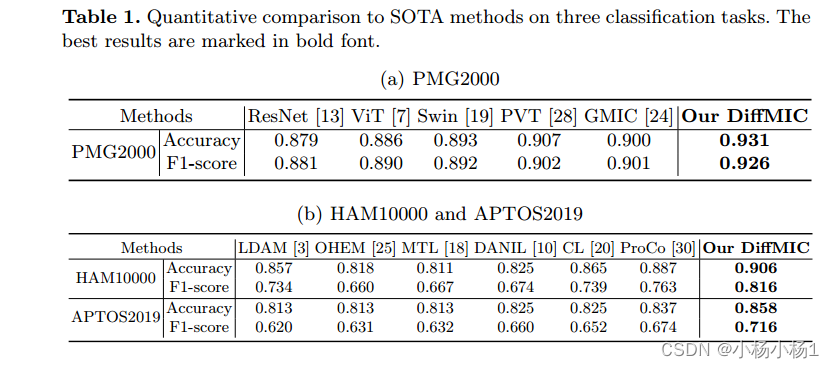
用于医学图像分类的双引导的扩散网络
文章目录 DiffMIC: Dual-Guidance Diffusion Network for Medical Image Classification摘要本文方法实验结果 DiffMIC: Dual-Guidance Diffusion Network for Medical Image Classification 摘要 近年来,扩散概率模型在生成图像建模中表现出了显著的性能…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
