无穷限积分习题
前置知识:无穷限积分
习题1
计算 ∫ 1 + ∞ ln x x 2 d x \int_1^{+\infty}\dfrac{\ln x}{x^2}dx ∫1+∞x2lnxdx
解:
\qquad 原式 = ( − ln x x ) ∣ 1 + ∞ + ∫ 1 + ∞ 1 x 2 d x = ( − ln x x ) ∣ 1 + ∞ + ( − 1 x ) ∣ 1 + ∞ =(-\dfrac{\ln x}{x})\bigg\vert_1^{+\infty}+\int_1^{+\infty}\dfrac{1}{x^2}dx=(-\dfrac{\ln x}{x})\bigg\vert_1^{+\infty}+(-\dfrac 1x)\bigg\vert_1^{+\infty} =(−xlnx) 1+∞+∫1+∞x21dx=(−xlnx) 1+∞+(−x1) 1+∞
= ( − 0 + 0 ) + ( − 0 + 1 ) = 1 \qquad\quad \ \ \ =(-0+0)+(-0+1)=1 =(−0+0)+(−0+1)=1
其中, lim x → + ∞ ln x x \lim\limits_{x\to +\infty}\dfrac{\ln x}{x} x→+∞limxlnx由洛必达法则可得为 0 0 0。
习题2
计算 ∫ − ∞ + ∞ 1 x 2 + 2 x + 2 d x \int_{-\infty}^{+\infty}\dfrac{1}{x^2+2x+2}dx ∫−∞+∞x2+2x+21dx
解:
\qquad 原式 = ∫ − ∞ + ∞ 1 1 + ( x + 1 ) 2 d ( x + 1 ) = arctan ( x + 1 ) ∣ − ∞ + ∞ =\int_{-\infty}^{+\infty}\dfrac{1}{1+(x+1)^2}d(x+1)=\arctan(x+1)\bigg\vert_{-\infty}^{+\infty} =∫−∞+∞1+(x+1)21d(x+1)=arctan(x+1) −∞+∞
= lim x → + ∞ arctan x − lim x → − ∞ arctan x = π 2 − ( − π 2 ) = π \qquad\quad \ \ \ =\lim\limits_{x\to +\infty}\arctan x-\lim\limits_{x\to -\infty}\arctan x=\dfrac{\pi}{2}-(-\dfrac{\pi}{2})=\pi =x→+∞limarctanx−x→−∞limarctanx=2π−(−2π)=π
习题3
计算 ∫ − ∞ + ∞ 1 e x + e 2 − x d x \int_{-\infty}^{+\infty}\dfrac{1}{e^x+e^{2-x}}dx ∫−∞+∞ex+e2−x1dx
解:
\qquad 原式 = ∫ − ∞ + ∞ 1 e 2 − x ( e 2 x − 2 + 1 ) d x = 1 e ∫ − ∞ + ∞ e x − 1 ( e x − 1 ) 2 + 1 d x =\int_{-\infty}^{+\infty}\dfrac{1}{e^{2-x}(e^{2x-2}+1)}dx=\dfrac 1e\int_{-\infty}^{+\infty}\dfrac{e^{x-1}}{(e^{x-1})^2+1}dx =∫−∞+∞e2−x(e2x−2+1)1dx=e1∫−∞+∞(ex−1)2+1ex−1dx
= 1 e ( arctan e x − 1 ) ∣ − ∞ + ∞ = 1 e ( π 2 − 0 ) = π 2 e \qquad\quad \ \ \ =\dfrac 1e(\arctan e^{x-1})\bigg\vert_{-\infty}^{+\infty}=\dfrac 1e(\dfrac{\pi}{2}-0)=\dfrac{\pi}{2e} =e1(arctanex−1) −∞+∞=e1(2π−0)=2eπ
习题4
设 p > 0 p>0 p>0,求 ∫ 1 + ∞ 1 x p d x \int_1^{+\infty}\dfrac{1}{x^p}dx ∫1+∞xp1dx的收敛性。
解:
∫ 1 b 1 x p d x = { ln b , p = 1 b 1 − p − 1 1 − p , p ≠ 1 \int_1^{b}\dfrac{1}{x^p}dx= \left\{\begin{matrix} \ln b, \qquad\quad \ p=1 \\ \qquad \\ \dfrac{b^{1-p}-1}{1-p}, \quad p\neq 1 \end{matrix}\right. ∫1bxp1dx=⎩ ⎨ ⎧lnb, p=11−pb1−p−1,p=1
\qquad 当 0 < p < 1 0<p<1 0<p<1时, lim b → + ∞ 1 x p d x = b 1 − p − 1 1 − p → + ∞ \lim\limits_{b\to +\infty}\dfrac{1}{x^p}dx=\dfrac{b^{1-p}-1}{1-p}\to +\infty b→+∞limxp1dx=1−pb1−p−1→+∞
\qquad 当 p = 1 p=1 p=1时, lim b → + ∞ 1 x p d x = ln b → + ∞ \lim\limits_{b\to +\infty}\dfrac{1}{x^p}dx=\ln b\to +\infty b→+∞limxp1dx=lnb→+∞
\qquad 当 p > 1 p>1 p>1时, lim b → + ∞ 1 x p d x = 1 p − 1 \lim\limits_{b\to +\infty}\dfrac{1}{x^p}dx=\dfrac{1}{p-1} b→+∞limxp1dx=p−11
\qquad 综上所述, ∫ 1 + ∞ 1 x p d x \int_1^{+\infty}\dfrac{1}{x^p}dx ∫1+∞xp1dx在 0 < p ≤ 1 0<p\leq 1 0<p≤1时发散,在 p > 1 p>1 p>1时收敛
总结
在一般情况下,无穷限积分可以和普通积分一样进行变换。有良好的微积分的基础,才能够很好地学习这类知识。
相关文章:

无穷限积分习题
前置知识:无穷限积分 习题1 计算 ∫ 1 ∞ ln x x 2 d x \int_1^{\infty}\dfrac{\ln x}{x^2}dx ∫1∞x2lnxdx 解: \qquad 原式 ( − ln x x ) ∣ 1 ∞ ∫ 1 ∞ 1 x 2 d x ( − ln x x ) ∣ 1 ∞ ( − 1 x ) ∣ 1 ∞ (-\dfrac{\…...

AI 3D结构光技术加持,小米引领智能门锁新标准
一直以来,小米智能门锁系列产品让更多家庭走进了安全便捷的智能生活,安全至上的设计让很多家庭都轻松告别了随身钥匙。 7月27日,小米正式推出小米智能门锁M20 Pro,再一次引领智能门锁产品的发展潮流。该款门锁采用AI 3D结构光技术…...

管理类联考——逻辑——形式逻辑——汇总篇
简述 形式逻辑: 识别题型:逻辑符号表达及标志词:联假言符号化特殊命题“除非否则”;五大关系:矛盾、等价、包含、至少有一真、至少有一假;【通过“关系”,串联起“假联选”言】 识别题型&…...

架构的分类
目录 一、 RUP41 架构 1.1 RUP41架构方法概述 1.2 RUP41架构总体 1.3 RUP41架构方法内容 1.3.1 逻辑视图 1.3.2 开发视图 1.3.3 物理视图 1.3.4 处理视图 1.3.5 场景视图 二、 TOGAF9 架构 2.1 TOGAF9 架构概述 2.2 TOGAF9 架构分类 2.2.1 业务架构 2.2.2 数据架…...

[SQL挖掘机] - 窗口函数 - lag
介绍: lag() 是一种常用的窗口函数,它用于获取某一行之前的行的值。它可以用来在结果集中的当前行之前访问指定列的值。 用法: lag() 函数的语法如下: lag(列名, 偏移量, 默认值) over (partition by 列名1, 列名2, ... order by 列名 [asc|desc], .…...

springboot项目如何自动重启(使用Devtools检测修改并自动重启springboot)
1. 问题: 我们在项目开发阶段,可能经常会修改代码,修改完后就要重启Spring Boot。经常手动停止再启动,比较麻烦。 所以我们引入一个Spring Boot提供的开发工具; 只要源码或配置文件发生修改,Spring Boot应用…...
docker: Error response from daemon: No command specified.
执行 docker run -it -d -v /home/dell/workspace/workspace/test_192.168.1.202_pipeline:/home/workspace1 --name test_192.168.1.202_pipeline_10 qnx:7.1报错 问题定位:export导入的镜像需要带上command,以下命令查看command信息 docker ps --no…...

百度地图点标记加调用
先看效果 PHP代码 <?phpnamespace kds_addons\edata\controller;use think\addons\Controller; use think\Db;class Maps extends Controller {// 经纬度计算面积function calculate_area($points){$totalArea 0;$numPoints count($points);if ($numPoints > 2) {f…...
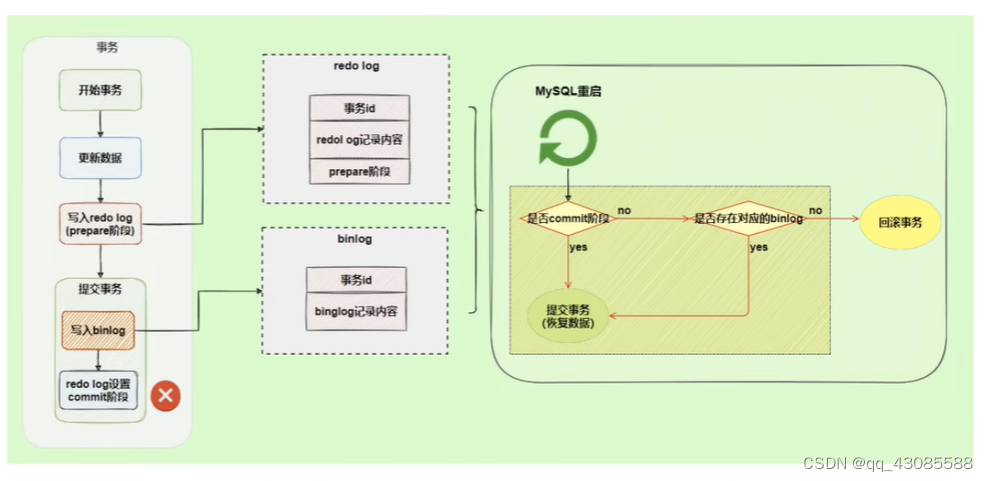
MySQL 其他数据库日志
我们了解数据库事务时,知道两种日志:重做日志,回滚日志。 对于线上数据库应用系统,突然遭遇 数据库宕机 怎么办?在这种情况下,定位宕机的原因 就非常关键。我们可以查看数据库的 错误日志。因为日志中记录…...

为何企业和开发团队应该重视进行兼容性测试
随着科技的不断进步和软件的广泛应用,保证软件在不同平台和环境下正常运行变得至关重要。本文将探讨软件兼容性测试的重要性和好处,并介绍为何企业和开发团队应该重视进行兼容性测试,以确保软件的稳定性和用户体验。 提供用户友好的体验 软件…...

牛客网Verilog刷题——VL51
牛客网Verilog刷题——VL51 题目答案 题目 请编写一个十六进制计数器模块,计数器输出信号递增每次到达0,给出指示信号zero,当置位信号set 有效时,将当前输出置为输入的数值set_num。模块的接口信号图如下: 模块的时序图…...

从零实现深度学习框架——Transformer从菜鸟到高手(一)
引言 💡本文为🔗[从零实现深度学习框架]系列文章内部限免文章,更多限免文章见 🔗专栏目录。 本着“凡我不能创造的,我就不能理解”的思想,系列文章会基于纯Python和NumPy从零创建自己的类PyTorch深度学习框…...
数组指针
数组指针的定义 1.数组指针是指针还是数组? 指针。 int a 10;int* p &a;//指向整型数据的指针 char b w;char* q &b;//指向字符变量的指针 所以数组指针应该是指向数组的指针。 2.数组指针应该怎么定义? int arr[10] { 0 };int(*p)[10] …...

C++设计模式之过滤器设计模式
C过滤器设计模式 什么是过滤器设计模式 过滤器设计模式是一种行为型设计模式,它允许你在特定的条件下对输入或输出进行过滤,以便实现不同的功能。 该模式有什么优缺点 优点 可扩展性:过滤器设计模式允许您轻松地添加、删除或替换过滤器&a…...
)
SpringBoot整合RedisTemplate操作Redis数据库详解(提供Gitee源码)
前言:简单分享一下我在实际开发当中如何使用SpringBoot操作Redis数据库的技术分享,完整的代码我都提供了出来,大家按需复制使用即可! 目录 一、导入pom依赖 二、yml配置文件 三、使用FastJson序列化 四、核心配置类 五、工具…...

SQL 执行计划管理(SPM)
一、SPM 需求背景 任何数据库应用程序的性能在很大程度上都依赖于查询执行,尽管优化器无需用户干预就可以评估最佳计划,但是 SQL 语句的执行计划仍可能由于以下多种原因发生意外更改:版本升级、重新收集优化器统计信息、改变优化器参数或模式…...
浅谈微服务异步解决方案
导言 异步是一种设计思想,不是设计目的,因此不要为了异步而异步,要有所为,有所不为。 异步不是『银弹』, 避免试图套用一个『异步框架』解决所有问题, 需要根据不同的业务特点或要求,选择合适的…...
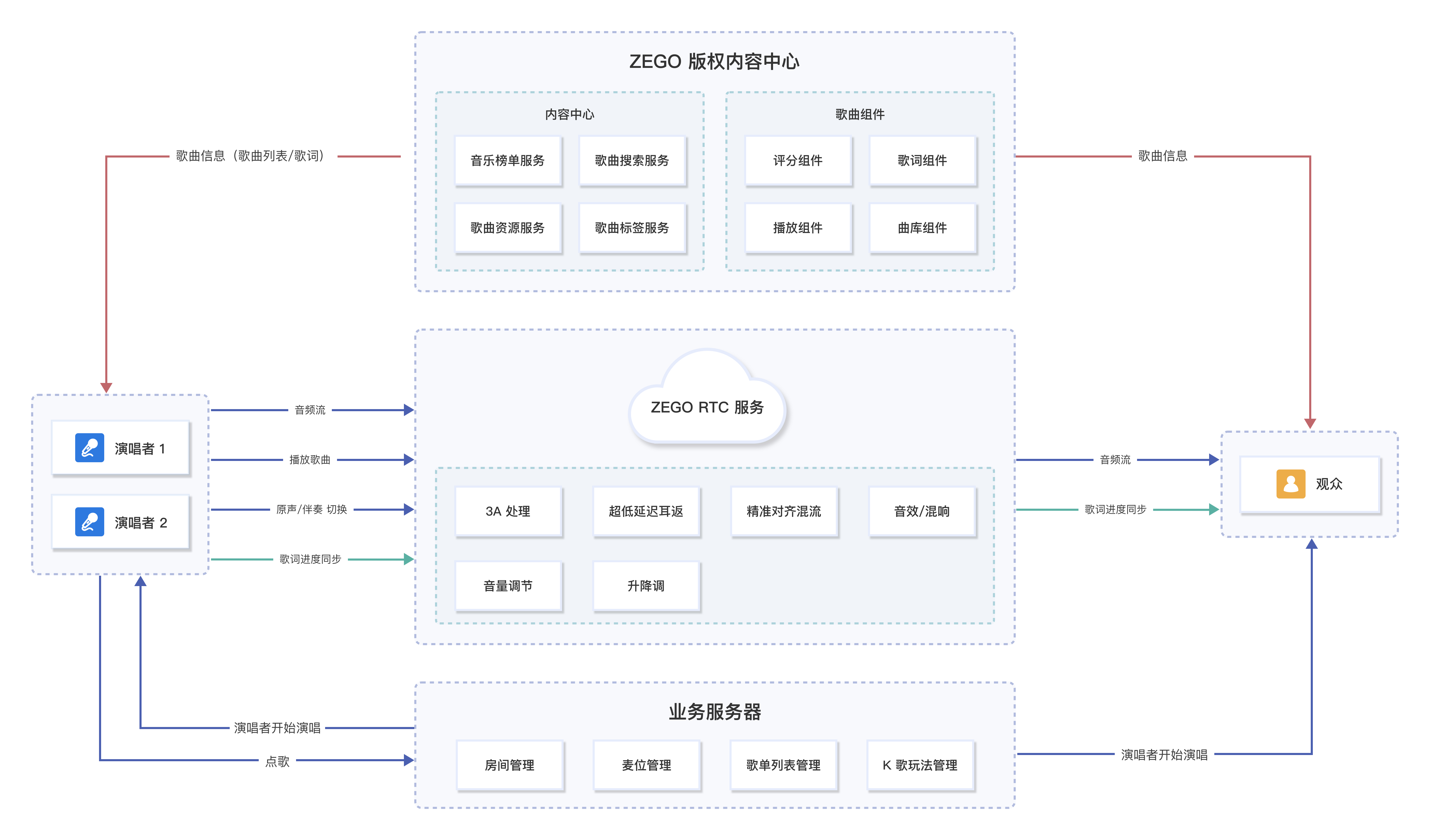
【音视频SDK测评】线上K歌软件开发技术选型
摘要 在线K歌软件的开发有许多技术难点,需考虑到音频录制和处理、实时音频传输和同步、音频压缩和解压缩、设备兼容性问题等技术难点外,此外,开发者还应关注音乐版权问题,确保开发的应用合规合法。 前言 前面写了几期关于直播 …...

Jackson:String转object反序列化失败
场景 消费mq时String转Object 代码 for (MessageExt msg : msgs) {String msgBody new String(msg.getBody(), StandardCharsets.UTF_8);BinlogEvent binlogEvent JsonUtil.silentString2Object(msgBody, BinlogEvent.class);binlogEvent.setPort(Long.valueOf(port));tCo…...

Spark_Core---6
spark 相关概念补充 课程目标 了解spark的安装部署知道spark作业提交集群的过程 6.1 spark的安装部署 1、下载spark安装包 http://spark.apache.org/downloads.html 高版本不存在cdh的编译版本,可以从官网下载源码版本,指定高版本hadoop进行编译 编译…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
