搜索与图论(二)
最短路
单源最短路
所有边权都是正数
朴素Dijkstra算法
基本思路:从1号点到其他点的最短距离
步骤:
定义一个s集合包含当前已确定最短距离的点
1、初始化距离dis[1] = 0,dis[其它] = 正无穷
2、for i 0-n循环n次
2.1找到不在s中的距离最近的点 ->t
2.2把t加到s当中去
2.3用t来更新其它点的距离
模板代码如下:
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 510;
int n,m;
int g[N][N];
//dis表示从1号点到其它点的距离
int dist[N];
//st表示每个点的最短路是否确定
bool st[N];int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;for(int i = 0;i < n; i ++){int t = -1;for(int j = 1;j <= n;j ++)if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;st[t] = true;for(int j = 1;j <= n;j ++)dist[j] = min(dist[j],dist[t] + g[i][j]);}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
int main()
{scanf("%d%d", &n, &m);//初始化memset(g,0x3f,sizeof g);int t = dijkstra();printf("%d\n",t);return 0;
}
堆优化版的Dijkstra算法
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queque>using namespace std;const int N = 100010;
int n,m;
//存储方式改为邻接表的形式
int h[N],w[N],e[N],ne[N],idx;
//dis表示从1号点到其它点的距离
int dist[N];
//st表示每个点的最短路是否确定
bool st[N];void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;priority_queue<PII,vector<PII>,greater<PII>> heap;heap.push({0,1});while(heap.size --){auto t = heap.top();heap.pop();int ver = t.second,distance = t.first();if (st[ver]) continue;for(int i = h[ver];i != -1;i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j],j});}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
int main()
{scanf("%d%d", &n, &m);//初始化memset(h,-1,sizeof h);while(m --){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);}int t = dijkstra();printf("%d\n",t);return 0;
}
存在负权边
Bellman-Ford算法
基本思路:n次迭代,每次循环所有边,每次循环更新最短距离
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int M = 100010, N = 510;int n,m,k;
int dist[N],backup[N];struct Edge
{int a,b,w;}edges[M];int bellman_ford()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;for(int i = 0;i < k;i ++){//保存上一次的结果memcpy(backup,dist,sizeof dist);for(int j = 0;j < m;j ++){int a = edges[j].a,b = edges[j].b,w = edges[j].w;dist[b] = min(dist[b],backup[a] + w);}}if(dist[n] > 0x3f3f3f3f / 2) return -1;return dist[n];
}int main()
{scanf("%d%d%d",&n,&m,&k);for(int i = 0;i < m;i ++){int a,b,w;scanf("%d%d%d",&a,&b,&w);edges[i] = {a,b,w};}int t = bellman_ford();if(t == -1){puts("impossible");}else printf("%d\n",t);return 0;
}
SPFA算法
对Bellman-Ford算法的一个优化
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queque>using namespace std;const int N = 100010;
int n,m;
//存储方式改为邻接表的形式
int h[N],w[N],e[N],ne[N],idx;
//dis表示从1号点到其它点的距离
int dist[N];
//st表示每个点的最短路是否确定
bool st[N];void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}int spfa()
{memset(dist,0x3f,sizeof dist);queue<int> q;q.push(1);st[1] = true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t];i != -1;i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if(!st[j]){q.push(j);st[j] = true;}}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];}
int main()
{scanf("%d%d", &n, &m);//初始化memset(h,-1,sizeof h);while(m --){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);}int t = spfa();if(t == -1) puts("false");else printf("%d\n",t);return 0;
}
多源汇最短路
Floyd
利用临界矩阵来存储
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 210,INF = 1e9;int n,m,Q;
int d[N][N];void floyd()
{for(int k = 1;k <= n;k ++)for(int i = 1;i <= n;i ++)for(int j = 1;j <= n;j ++)d[i][j] = min(d[i][j],d[i][k] + d[k][j]);
}
int main()
{scanf("%d%d%d",&n,&m,&Q);for(int i = 1;i <= n;i ++){for(int j = 1;j <= n;j ++)if(i == j) d[i][j] = 0;else d[i][j] = INF;}while(m --){int a,b,w;scanf("%d%d%d",&a,&b,&w);d[a][b] = min(d[a][b],w);}floyd();while(Q --){int a,b;scanf("%d%d",&a,&b);if(d[a][b] > INF / 2) puts("impossible");printf("%d\n",d[a][b]);}return 0;
}
相关文章:
)
搜索与图论(二)
最短路 单源最短路 所有边权都是正数 朴素Dijkstra算法 基本思路:从1号点到其他点的最短距离 步骤: 定义一个s集合包含当前已确定最短距离的点 1、初始化距离dis[1] 0,dis[其它] 正无穷 2、for i 0-n循环n次 2.1找到不在s中的距离最近的点 ->t 2.2把t加到s当中去…...
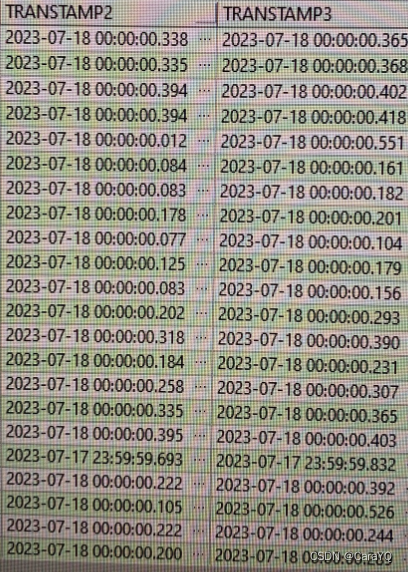
【SQL】-【计算两个varchar类型的timestamp的毫秒差】
背景 TRANSTAMP3、TRANSTAMP2在Oracle数据库中的类型为varchar,但实际保存的值是时间戳timestamp类型,现在要计算二者的毫秒差 Oracle或MySQL extract(second from (to_timestamp(TRANSTAMP3,yyyy-mm-dd hh24:mi:ss.ff) - to_timestamp(TRANSTAMP2,yyy…...
)
Java 微信商家打款到零钱(旧版本接口)
旧版微信支付接口要求请求时携带证书请求 构建请求参数 /*** 付款到零钱** param withdrawalDto dto撤军* return {link Map }<{link String }, {link Object }>* throws Exception 异常* Author chen 2023-07-27 15:04*/private Map<String, Object> payToUser(Wi…...

Vue+Element ui Study
目录 一、VueElement ui 1、show-overflow-tooltip属性设置宽度 2、this.$refs使用方法 Error in v-on handler: “TypeError: Cannot read properties of undefined (reading ‘xxx‘)“ 一、VueElement ui 1、show-overflow-tooltip属性设置宽度 :show-overflow-toolti…...
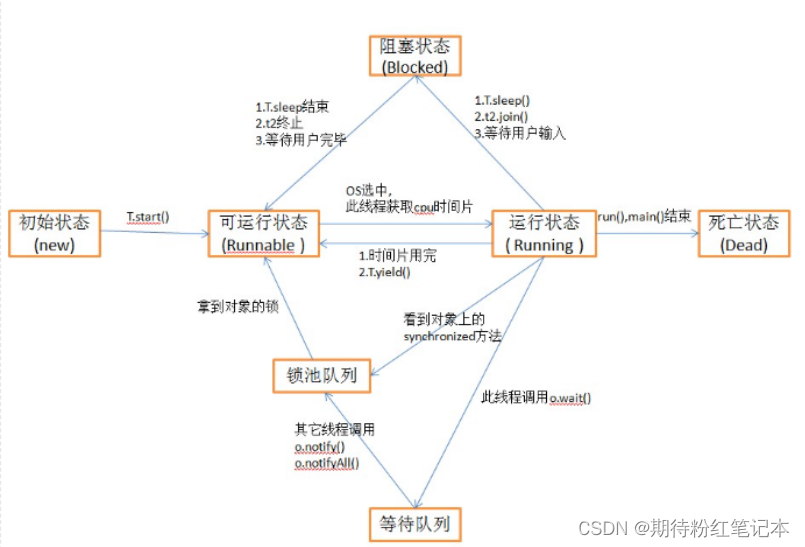
JAVA基础-多线程入门(详解)
目录 引言 一,线程概念 二,创建线程 2.1,继承Thread类,重写run方法 2.2,实现Runnable接口,重写run方法,实现Runnable接口的实现类的实例对象作为Thread构造函 数的target 2.3,通…...

Cirno‘s Perfect Equation Class 2023牛客暑期多校训练营5 D
登录—专业IT笔试面试备考平台_牛客网 题目大意:有q次询问,每次给出三个整数k,c,n,求有多少满足条件的数对(a,b)满足kabc且c是b的倍数,且gcd(a,b)>n 1<q<100;…...
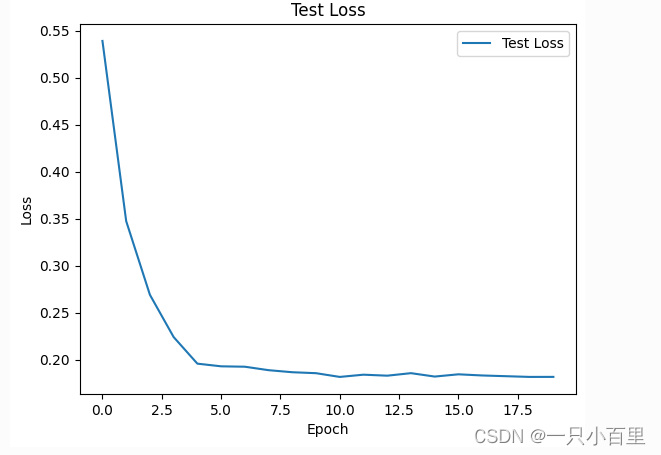
pytorch学习——如何构建一个神经网络——以手写数字识别为例
目录 一.概念介绍 1.1神经网络核心组件 1.2神经网络结构示意图 1.3使用pytorch构建神经网络的主要工具 二、实现手写数字识别 2.1环境 2.2主要步骤 2.3神经网络结构 2.4准备数据 2.4.1导入模块 2.4.2定义一些超参数 2.4.3下载数据并对数据进行预处理 2.4.4可视化数…...
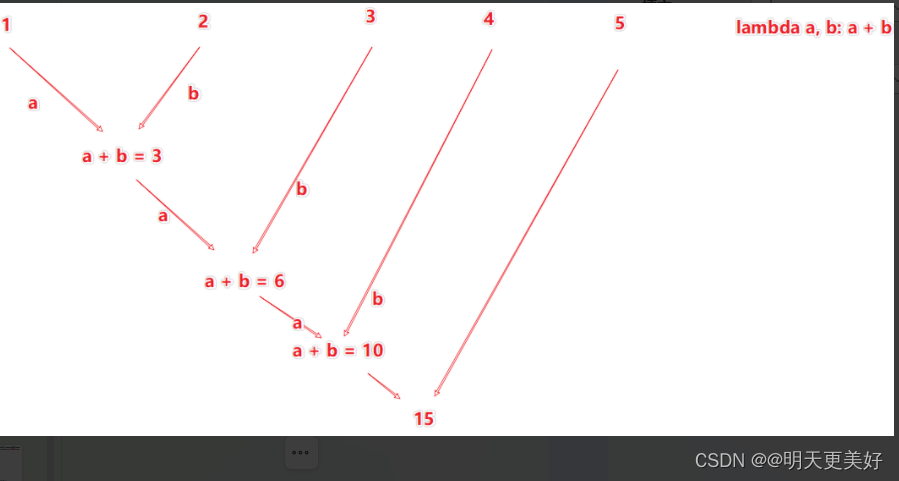
PySpark 数据操作
数据输入 RDD对象 如图可见,PySpark支持多种数据的输入,在输入完成后,都会得到一个:RDD类的对象 RDD全称为:弹性分布式数据集(Resilient Distributed Datasets) PySpark针对数据的处理&…...

FPGA2-采集OV5640乒乓缓存后经USB3.0发送到上位机显示
1.场景 基于特权A7系列开发板,采用OV5640摄像头实时采集图像数据,并将其经过USB3.0传输到上位机显示。这是验证数据流能力的很好的项目。其中,用到的软件版本,如下表所示,基本的硬件情况如下。该项目对应FPGA工程源码…...

亚信科技AntDB数据库专家参加向量数据库首次技术标准研讨会
2023年7月19日下午,中国通信标准化协会大数据技术标准推进委员会数据库与存储工作组(CCSA TC601 WG4)联合中国信通院数据库应用创新实验室(CAICT DBL)在线上召开《向量数据库技术要求》标准首次研讨会。本次会议由中国…...

Windows中实现右键把电子书通过邮件发到kindle
不使用第三方软件,通过Windows自带的函数,可以实现右键将电子书通过电子邮件发送到kindle邮箱,从而实现kindle电子书传送功能。实现过程如下: 1. 使用bat添加右键功能 打开资源管理器,在地址中输入%APPDATA%\Microso…...

Three.js之创建3D场景
参考资料 【G】Three.js官方文档:https://threejs.org/docs/ Three.js是一个流行的WebGL库,官方文档提供了详细的API参考和示例,适合学习和参考。【G】Three.js GitHub链接:https://github.com/mrdoob/three.js 这是一个流行的基…...
一个3年Android的找工作记录
作者:Petterp 这是我最近 1个月 的找工作记录,希望这些经历对你会有所帮助。 有时机会就像一阵风,如果没有握住,那下一阵风什么时候吹来,往往是个运气问题。 写在开始 先说背景: 自考本,3年经验࿰…...

CAS原理解析
CAS是一种乐观锁机制,一种比较并交换的过程和理念,用来解决线程安全问题,具体来讲就是对共享变量值的安全更新机制。能够保证原子、可见、一致性。这种交换过程是在Unsafe类中实现。 从一段简单的代码开始来对源码做分析 public static void…...
SQL项目实战:银行客户分析
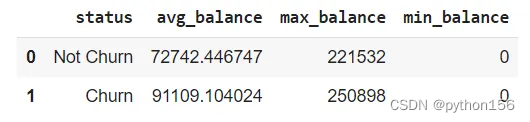
大家好,本文将与大家分享一个SQL项目,即根据从数据集收集到的信息分析银行客户流失的可能性。这些洞察来自个人信息,如年龄、性别、收入和人口统计信息、银行卡类型、产品、客户信用评分以及客户在银行的服务时间长短等。对于银行而言&#x…...
)
【Redis深度专题】「核心技术提升」探究Redis服务启动的过程机制的技术原理和流程分析的指南(集群指令分析—实战篇)
探究Redis服务启动的过程机制的技术原理和流程分析的指南(集群指令分析—下篇) Cluster XX的集群指令(扩展)写入记录主节点和备节点切换-CLUSTER FAILOVER新加入master节点新加入slave节点为slave节点重新分配master分配哈希槽删除…...

ubuntu
安装 sudo apt-get update sudo apt-get install mysql-server mysql-client 设置root密码 cat /etc/mysql/debian.cnf 查看默认密码 mysql -u debian-sys-maint -p 连接输入密码 use mysql; select user,plugin from user; update user set pluginmysql_native_passwor…...
【芯片设计- RTL 数字逻辑设计入门 3- Verdi 常用使用命令】
文章目录 Verdi 全局显示Verdi 前导 0 的显示Verdi 数据笔数统计Verdi 波形数据dump Verdi 全局显示 bsubi -n 16 -J sam visualizer -tracedir ./veloce.wave/debug_waveform.stw 打开波形后,如果想要看到所有信号的数据,可以点击下图中红框中的按钮&a…...
python-pytorch基础之cifar10数据集使用图片分类
这里写目录标题 总体思路获取数据集下载cifar10数据解压包文件介绍加载图片数字化信息查看数据信息数据读取自定义dataset使用loader加载建模训练测试建测试数据的loader测试准确性测试一张图片读取一张图片加载模型预测图片类型创建一个预测函数随便来张马的图片结果其他打开一…...

华纳云:linux下磁盘管理与挂载硬盘方法是什么
在Linux下进行磁盘管理和挂载硬盘的方法如下: 磁盘管理: a. 查看已连接的磁盘:可以使用命令 fdisk -l 或 lsblk 查看系统中已连接的磁盘信息,包括硬盘和分区。 b. 创建分区:如果磁盘是全新的,需要使用 f…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
