机器学习笔记之优化算法(六)线搜索方法(步长角度;非精确搜索;Glodstein Condition)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索,Glodstein Condition]
引言
上一节介绍了 Armijo \text{Armijo} Armijo准则 ( Armijo Condition ) (\text{Armijo Condition}) (Armijo Condition),本节将继续介绍 Glodstein \text{Glodstein} Glodstein准则 ( Glodstein Condition ) (\text{Glodstein Condition}) (Glodstein Condition)。
回顾: Armijo Condition \text{Armijo Condition} Armijo Condition
首先,希望数值解对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞收敛至最优解 f ∗ f^* f∗:
{ f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗
而数值解对应的目标函数结果满足严格的单调性是一项不可忽视的重要因素:
{ f ( x k + 1 ) = f ( x k + α ⋅ P k ) = ϕ ( α ) ϕ ( α ) = f ( x k + 1 ) < f ( x k ) = ϕ ( 0 ) \begin{cases} \begin{aligned} & f(x_{k+1}) = f(x_k + \alpha \cdot \mathcal P_k) = \phi(\alpha) \\ & \phi(\alpha) = f(x_{k+1}) < f(x_k) = \phi(0) \end{aligned} \end{cases} {f(xk+1)=f(xk+α⋅Pk)=ϕ(α)ϕ(α)=f(xk+1)<f(xk)=ϕ(0)
但仅仅满足 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞服从严格的单调性不足以证明 { f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗。也就是说:后者是前者的必要不充分条件。
关于不充分性质的反例,见传送门
Armijo \text{Armijo} Armijo准则产生的动机在于:条件 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)的约束能力太松散。而具体表现在: ϕ ( α ) \phi(\alpha) ϕ(α)函数中,满足条件 f ( x k + 1 ) < f ( x k ) f(x_{k+1})< f(x_k) f(xk+1)<f(xk)的 α \alpha α值过多,反而对优秀步长结果的选择产生阻碍:

观察上图,其中:
- 蓝色曲线表示 ϕ ( α ) \phi(\alpha) ϕ(α)的函数曲线;
- 红色虚线表示步长 α \alpha α的划分边界 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)。因而 f ( x k + 1 ) < f ( x k ) f(x_{k+1})< f(x_k) f(xk+1)<f(xk)描述的是红色虚线下方的部分,具体对应步长 α \alpha α的选择范围见 α \alpha α轴上的红色实线。
Armijo Condition \text{Armijo Condition} Armijo Condition关于 f ( x k + 1 ) < f ( x k ) f(x_{k+1})< f(x_k) f(xk+1)<f(xk)条件过于松散的处理方法是:相比于上图中的红色虚线,尝试找到一条更优的直线对 ϕ ( α ) \phi(\alpha) ϕ(α)进行划分,最终使步长 α \alpha α的选择范围明显降低。
它选择了 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)与 ϕ ( α ) \phi(\alpha) ϕ(α)在 α = 0 \alpha=0 α=0处的切线函数: l ( α ) = f ( x k ) + [ ∇ f ( x k ) ] T P k ⋅ α l(\alpha) = f(x_k) + [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha l(α)=f(xk)+[∇f(xk)]TPk⋅α进行组合,其划分边界函数表示为:
L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α C 1 ∈ ( 0 , 1 ) \mathcal L(\alpha) = f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \quad \mathcal C_1 \in (0,1) L(α)=f(xk)+C1⋅[∇f(xk)]TPk⋅αC1∈(0,1)
由于 C 1 > 0 , α > 0 \mathcal C_1 >0,\alpha>0 C1>0,α>0(步长的物理意义);并且 [ ∇ f ( x k ) ] T P k < 0 \left[\nabla f(x_k)\right]^T \mathcal P_k < 0 [∇f(xk)]TPk<0,因此函数 L ( α ) \mathcal L(\alpha) L(α)的斜率存在:
关于 [ ∇ f ( x k ) ] T P k < 0 [\nabla f(x_k)]^T \mathcal P_k < 0 [∇f(xk)]TPk<0详见优化算法——下降方向的推导过程
- 上界: 0 0 0(无法取到),此时 L ( α ) \mathcal L(\alpha) L(α)的函数图像与 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)的函数图像重合;
- 下界: [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk(无法取到),此时 L ( α ) \mathcal L(\alpha) L(α)的函数图像与 l ( α ) l(\alpha) l(α)的函数图像重合。
对应函数图像表示如下。可以看到:相比上图, α \alpha α轴上绿色实线描述的步长 α \alpha α的选择范围明显小于上图中红色实线描述的范围。从而对最优步长 α \alpha α的选择进行优化。
这里并没有涉及证明过程,仅是从逻辑角度进行描述。

关于为什么要选择 l ( α ) l(\alpha) l(α)的斜率 [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk作为下界的描述 ? ? ?主要是因为:该切线函数在局部范围内的函数图像(凸函数)中不存在位于该切线下方的函数结果。但这仅仅作用于局部范围。因为我们对完整的 ϕ ( α ) \phi(\alpha) ϕ(α)函数未知,在全局范围中可能存在函数信息位于 l ( α ) l(\alpha) l(α)下方。例如下图描述的 ϕ ( α ) \phi(\alpha) ϕ(α)函数:

因此,斜率 [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk并不是绝对下界。但不否认的是: l ( α ) l(\alpha) l(α)的斜率用于划分有效的 α \alpha α步长来说是苛刻的,至少比 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)描述的范围更加严格。
关于 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端
关于 Armijo \text{Armijo} Armijo规则,我们仅从 L ( α ) \mathcal L(\alpha) L(α)公式的角度也能看出它相比 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) <f(x_k) f(xk+1)<f(xk)更加严格:
f ( x k + 1 ) = ϕ ( α ) < L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ < 0 < f ( x k ) f(x_{k+1}) = \phi(\alpha) < \mathcal L(\alpha) = f(x_k) + \underbrace{\mathcal C_1\cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha}_{<0} <f(x_k) f(xk+1)=ϕ(α)<L(α)=f(xk)+<0 C1⋅[∇f(xk)]TPk⋅α<f(xk)
但 Armijo \text{Armijo} Armijo规则依然存在弊端:在 C 1 ∈ ( 0 , 1 ) \mathcal C_1 \in (0,1) C1∈(0,1)的选择过程中,依然存在:满足 ϕ ( α ) < L ( α ) \phi(\alpha) < \mathcal L(\alpha) ϕ(α)<L(α)的 α \alpha α结果过少,从而这些样本点包含的 α \alpha α范围过小。例如:
其中绿色实线描述 L ( α ) \mathcal L(\alpha) L(α),其对应的有效范围见 α \alpha α轴上的绿色实线。可以看出,覆盖的 α \alpha α范围极小并且对应的 ϕ ( α ) \phi(\alpha) ϕ(α)结果也不够优秀。

上述情况是有可能出现的,虽然我们并不执著最小值一定位于 ϕ ( α ) < L ( α ) \phi(\alpha) < \mathcal L(\alpha) ϕ(α)<L(α)所描述的 α \alpha α范围内(因为是求数值解),但我们同样希望:排除掉类似这种 α \alpha α较小,并且质量不高的情况,或者:我们更希望 ϕ ( α ) \phi(\alpha) ϕ(α)的核心部分有机会出现在范围内。
Glodstein Condition \text{Glodstein Condition} Glodstein Condition
Glodstein Consition \text{Glodstein Consition} Glodstein Consition是在 Armijo Condition \text{Armijo Condition} Armijo Condition的基础上,给 ϕ ( α ) \phi(\alpha) ϕ(α)的范围加上一个下界:
{ Glodstein Condition : f ( x k ) + C 2 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ Lower Bound ≤ ϕ ( α ) ≤ f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ Upper Bound;Armijo Condition C 1 + C 2 = 1 \begin{cases} \text{Glodstein Condition : }\underbrace{f(x_k) + \mathcal C_2 \cdot [\nabla f(x_k)]^T\mathcal P_k \cdot \alpha}_{\text{Lower Bound}} \leq \phi(\alpha) \leq \underbrace{f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha}_{\text{Upper Bound;Armijo Condition}} \\ \quad \\ \mathcal C_1 + \mathcal C_2 = 1 \end{cases} ⎩ ⎨ ⎧Glodstein Condition : Lower Bound f(xk)+C2⋅[∇f(xk)]TPk⋅α≤ϕ(α)≤Upper Bound;Armijo Condition f(xk)+C1⋅[∇f(xk)]TPk⋅αC1+C2=1
经过整理,使用一个参数 C \mathcal C C对上述范围进行描述:
f ( x k ) + ( 1 − C ) [ ∇ f ( x k ) ] T P k ⋅ α ≤ ϕ ( α ) ≤ f ( x k ) + C ⋅ [ ∇ f ( x k ) ] T P k α C ∈ ( 0 , 1 2 ) f(x_k) + (1 - \mathcal C) [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \leq \phi(\alpha) \leq f(x_k) + \mathcal C \cdot [\nabla f(x_k)]^T \mathcal P_k \alpha \quad \mathcal C \in \left(0,\frac{1}{2}\right) f(xk)+(1−C)[∇f(xk)]TPk⋅α≤ϕ(α)≤f(xk)+C⋅[∇f(xk)]TPkαC∈(0,21)
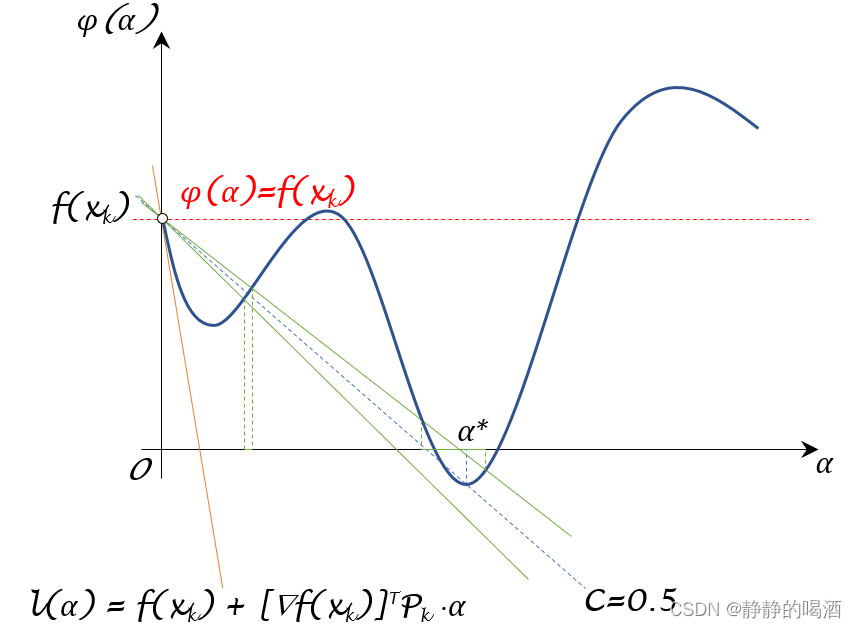
对应的函数图像表示如下:

其中两条绿色实线关于 f ( x k ) + 1 2 [ ∇ f ( x k ) ] T P k ⋅ α \begin{aligned}f(x_k) + \frac{1}{2} [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha\end{aligned} f(xk)+21[∇f(xk)]TPk⋅α(蓝色虚线)对称,两条绿色实线之间的范围就是 ϕ ( α ) \phi(\alpha) ϕ(α)有效的选择范围。其对应的 α \alpha α选择范围见上图 α \alpha α轴上的绿色实线。
从而可以通过修改 C \mathcal C C的数值,从而调整上图绿色实线之间的夹角。这种 ϕ ( α ) \phi(\alpha) ϕ(α)的选择方式极大程度地将 ϕ ( α ) \phi(\alpha) ϕ(α)的核心部分包含在选择范围内。从而缓解了 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端。
Goldstein Condition \text{Goldstein Condition} Goldstein Condition的弊端
即便 Goldstein Condition \text{Goldstein Condition} Goldstein Condition缓解了 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端。但其自身也同样存在弊端:当参数 C \mathcal C C接近 1 2 \begin{aligned}\frac{1}{2}\end{aligned} 21时,上下界均会朝着中心轴 f ( x k ) + 1 2 [ ∇ f ( x k ) ] T P k ⋅ α \begin{aligned}f(x_k) + \frac{1}{2} [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha\end{aligned} f(xk)+21[∇f(xk)]TPk⋅α方向靠拢。最终可能得到如下效果:
虽然这里描述的ϕ ( α ) \phi(\alpha) ϕ(α)范围还比较优秀,但这只是特例。在两条绿线之间的夹角极小时,我们映射出的ϕ ( α ) \phi(\alpha) ϕ(α)范围以及对应的α \alpha α范围都非常小,后面可能导致其将一些优质的α \alpha α结果给过滤掉。但与Armijo Condition \text{Armijo Condition} Armijo Condition相比,Goldstein Condition \text{Goldstein Condition} Goldstein Condition确实将选择范围集中在ϕ ( α ) \phi(\alpha) ϕ(α)的核心位置,而不是数量少的,较偏的ϕ ( α ) \phi(\alpha) ϕ(α)位置上。
下一节针对 Glodstein Condition \text{Glodstein Condition} Glodstein Condition因 C \mathcal C C值过于接近 1 2 \begin{aligned}\frac{1}{2}\end{aligned} 21而导致优质 α \alpha α结果被误杀的情况,我们介绍 Wolfe Condition \text{Wolfe Condition} Wolfe Condition。
相关参考:
【优化算法】线搜索方法-步长-Glodstein Condition
相关文章:

机器学习笔记之优化算法(六)线搜索方法(步长角度;非精确搜索;Glodstein Condition)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索,Glodstein Condition] 引言回顾: Armijo Condition \text{Armijo Condition} Armijo Condition关于 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端 Glodstein…...

Ant Design Pro 封装网络请求
可以直接在antdPro项目的app.tsx文件中对request进行运行时配置,并且该配置会直接透传到umi-request的全局配置。后续直接从umi中引入request或者useRequest直接使用,可以说是非常方便。文档可查看:umi.js 具体配置代码: import…...
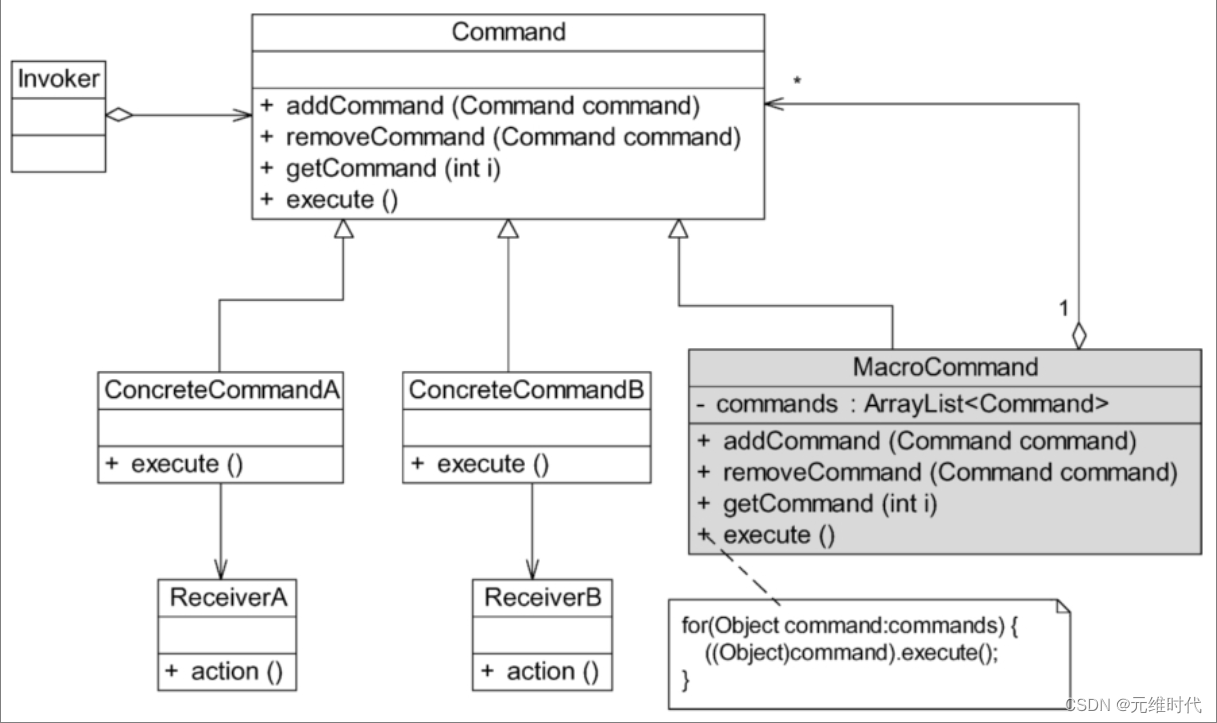
命令模式——请求发送者与接收者解耦
1、简介 1.1、概述 在软件开发中,经常需要向某些对象发送请求(调用其中的某个或某些方法),但是并不知道请求的接收者是谁,也不知道被请求的操作是哪个。此时,特别希望能够以一种松耦合的方式来设计软件&a…...

css 利用模糊属性 制作水滴
<style>.box {background-color: #111;height: 100vh;display: flex;justify-content: center;align-items: center;/* 对比度*/filter: contrast(20);}.drop {width: 150px;height: 159px;border-radius: 50%;background-color: #fff;position: absolute;/* 模糊 */filt…...

怎么才能提升自己工作能力?
表现最好的员工通常是获得加薪和工作晋升的人。您可以采取某些措施来提高您的工作绩效,并帮助您的主管将您视为他们最好的员工之一。在本文中,我们列出了 12 个技巧,可以立即提高您的工作绩效。 什么是工作绩效? 工作绩效是指您…...

Android Framework 之 Zygote
Android Zygote Android Zygote 是 Android 操作系统中一个关键的系统服务,它在系统启动时加载,为应用程序的运行提供了一种快速且资源高效的方式。 Zygote 的主要作用如下: 预加载共享库和类:Zygote 启动时,会预先加…...

二叉树的中序遍历 LeetCode热题100
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 思路 递归,按左中右的顺序添加节点。 利用栈先进后出的特性模拟递归。 代码 /**递归写法* Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left…...

IOS + Appium自动化教程
前言 项目闲置下来了,终于抽空有时间搞自动化了,看了下网上的教程基本通篇都是android自动化的介绍 ,ios自动化方面的内容网上简介的少之可怜。由于本人对ios自动化也是第一次做,甚至对苹果电脑的使用都不太熟悉,花了大…...

100个精选Python实战项目案例,在线无偿分享
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 随着 Python 语言的流行,越来越多的人加入到了 Python 的大家庭中。 为什么这么多人学 Python ? 我要喊出那句话了:“人生苦短,我用 Python!”, 正是…...

JSON语法
目录 一、JSON 语法规则 二、JSON 的两种结构: 三、JSON 名称/值对 JSON 值 JSON 数字 JSON 对象 JSON 数组 JSON 布尔值 JSON null 四、JSON 使用 JavaScript 语法 JSON 语法是 JavaScript 语法的子集。 一、JSON 语法规则 JSON 语法是 JavaScript 对象…...
PostMan+Jmeter+QTP工具介绍及安装
目录 一、PostMan介绍编辑 二、下载安装 三、Postman与Jmeter的区别 一、开发语言区别: 二、使用范围区别: 三、使用区别: 四、Jmeter安装 附一个详细的Jmeter按照新手使用教程,感谢作者,亲测有效。 五、Jme…...

2023电赛E题视觉部分
该部分主要要完成正方形区域的识别,并返回对应的坐标,但是由于距离1m,过远。因此需要引入图像增强,下面代码完成基本流程测试,仅供参考: import sensor import image import time # 初始化摄像头 senso…...

算法工程师岗位面试必备,讲透深度学习面试题,详解人工智能生成式任务与AI大模型面试题
DeepLearning-Interview-Awesome-2024 算法工程师岗位面试必备,讲透深度学习面试题,详解人工智能生成式任务与AI大模型面试题 实时更新题解链接:https://github.com/315386775/DeepLearing-Interview-Awesome-2024 记得点个关注࿰…...

JVM基础篇-虚拟机栈
JVM基础篇-虚拟机栈 定义 Java Virtual Machine Stacks (Java 虚拟机栈) 每个线程运行时所需要的内存,称为虚拟机栈每个栈由多个栈帧(Frame)组成,对应着每次方法调用时所占用的内存每个线程只能有一个活动…...
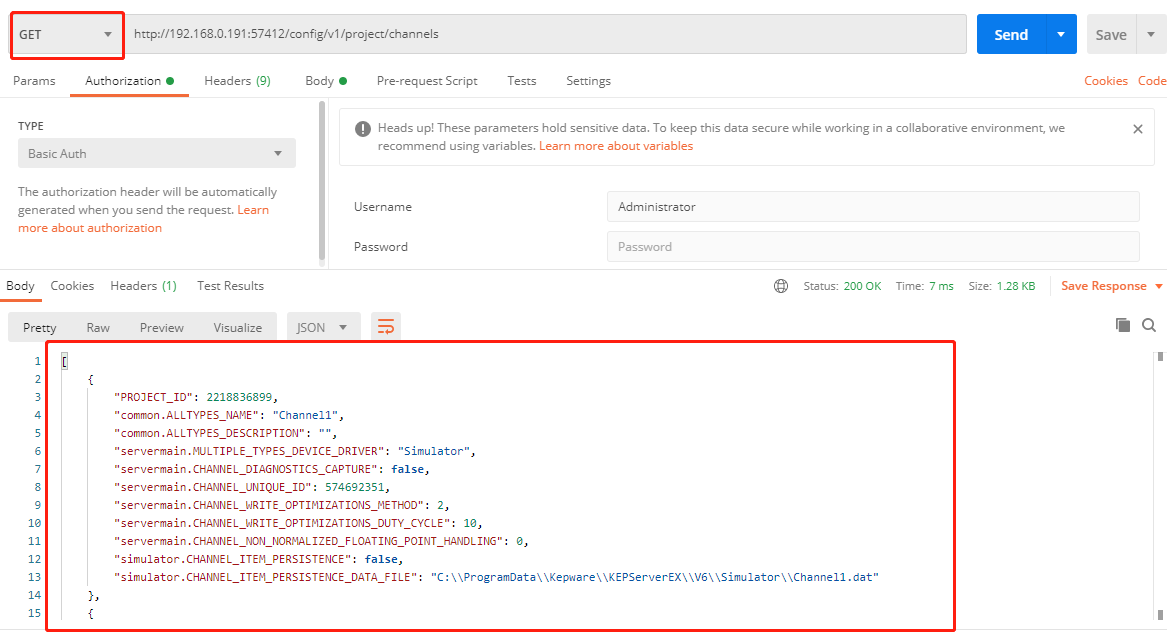
KepwareEX配置API REST接口
服务端Kepware设置 API允许连接设置 创建通道 请求地址(POST): https://<主机名_或_ip>:<端口>/config/v1/project/channels 以下示例使用postman工具访问API创建了一个名为Channel1 的通道,其使用在本地主机运行的服务器中的Simulator …...

【python】python求解矩阵的转置(详细讲解)
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...
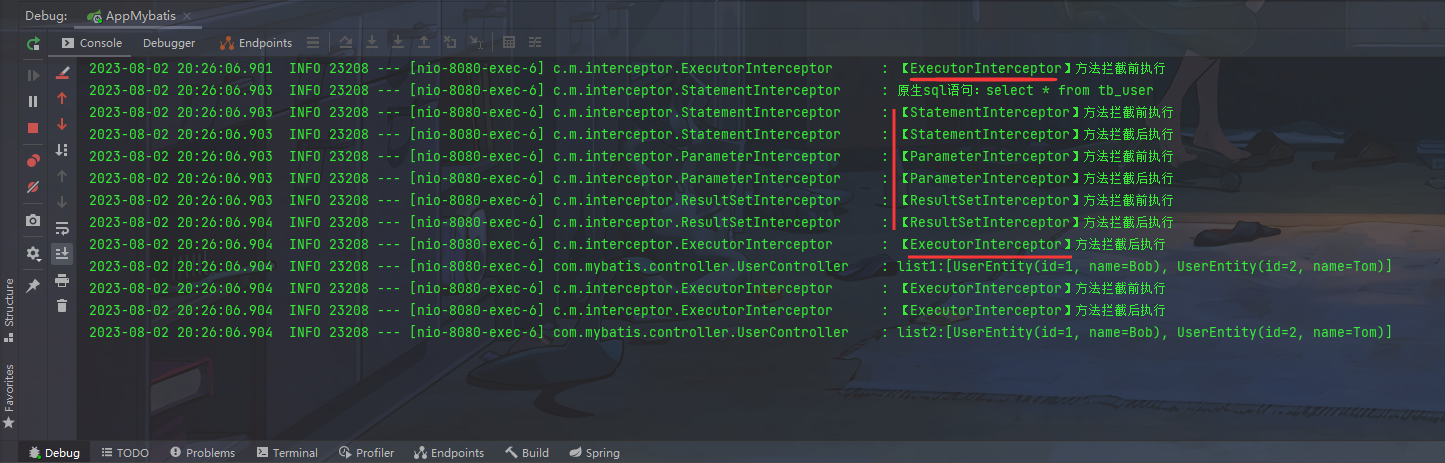
Mr. Cappuccino的第56杯咖啡——Mybatis拦截器
Mybatis拦截器 概述应用场景项目结构实现分页查询其它拦截器的使用 概述 Mybatis允许使用者在映射语句执行过程中的某一些指定的节点进行拦截调用,通过织入拦截器,在不同节点修改一些执行过程中的关键属性,从而影响SQL的生成、执行和返回结果…...
容器化安装环境EFK搭建
容器化安装环境 Docker中安装并启动ElasticSearch 前置配置 第一步:在宿主机上执行echo “net.ipv4.ip_forward1” >>/usr/lib/sysctl.d/00-system.conf 2.第二步:重启network和docker服务 [rootlocalhost /]# systemctl restart network &&…...
基于 Debian GNU/Linux 12 “书虫 “的Neptune 8.0 “Juna “来了
导读Neptune Linux 发行版背后的团队发布了 Neptune 8.0,作为这个基于 Debian 的 GNU/Linux 发行版的重大更新,它围绕最新的 KDE Plasma 桌面环境构建。 Neptune 8.0 被命名为 “Juna”,是在Neptune 7.5 发布 11 个月后发布的,也是…...
 Spatial Reference System篇 OGRSpatialReference类)
GDAL C++ API 学习之路 (4) Spatial Reference System篇 OGRSpatialReference类
class OGRSpatialReference #include <ogr_spatialref.h> OGRSpatialReference 是 GDAL/OGR 库中的一个重要类,用于管理和操作地理空间数据的空间参考系统(Spatial Reference System,SRS)。它提供了一系列功能&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
