论文笔记——Influence Maximization in Undirected Networks
Influence Maximization in Undirected Networks
- Contribution
- Motivation
- Preliminaries
- Notations
- Main results
- Reduction to Balanced Optimal Instances
- Proving Theorem 3.1 for Balanced Optimal Instances
Contribution
好久没发paper笔记了,这篇比较偏理论,可能边看边记比较高效一些,仅作为个人笔记,如有解读不到的还请包涵。这篇paper的贡献有两个,首先是证明了在无向图中使用greedy可以突破 1 − 1 / e 1-1/e 1−1/e的barrier(也就是greedy在无向图上会更强),达到 1 − 1 / e + c 1-1/e+c 1−1/e+c的近似,其中 c c c为常数;其次,该论文证明了无向图上的influence maximization是 A P X − h a r d APX-hard APX−hard。
Motivation
作者先给了一个比较紧的例子:

这里蓝色为OPT(optimal,最优解),红色为 G R D GRD GRD(greedy算法选择的种子节点)。注意,有向图中greedy选择 v 1 , v 2 v_1,v_2 v1,v2是因为 v a l ( v 1 ) = v a l ( v 2 ) = v a l ( v 3 ) = 1 val(v_1)=val(v_2)=val(v_3)=1 val(v1)=val(v2)=val(v3)=1。然而在无向图中,情况会更不一样:

这里 v a l val val为节点的影响力,同样,这里 O P T = { v 2 , v 3 } OPT = \{v_2,v_3\} OPT={v2,v3}(因为 v 2 , v 3 v_2,v_3 v2,v3的权重大),这里依然有 v a l ( { v 2 , v 3 } ) = 2 val(\{v_2,v_3\})=2 val({v2,v3})=2。然而贪心算法会可能会选择 G R D = { v 1 , v 2 } GRD = \{v_1,v_2\} GRD={v1,v2},且有 v a l ( v 2 ) = v a l ( v 3 ) = 1 + 0 + 1 ∗ 1 / 2 ∗ 1 / 2 = 5 / 4 val(v_2) =val(v_3) = 1 + 0 + 1 * 1/2 * 1/2 = 5/4 val(v2)=val(v3)=1+0+1∗1/2∗1/2=5/4,那么根据Greedy的习惯, G R D = { v 2 , v 3 } GRD = \{v_2,v_3\} GRD={v2,v3},也就是说,在这个例子中,greedy会选出最优解。
同样的结构,greedy在无向图和有向图上的表现却大相径庭,背后原因令人暖心:在无向图中,greedy选出的节点的影响力会和OPT的影响力重叠更少。然而这只是一个例子,不具备代表性,为了generalize这一现象,作者将使用 XYZ \textit{XYZ} XYZ lemma来构建反例(如下图)来说明在无向图中, k = 1 k=1 k=1时,greedy算法带来的近似比可以任意接近 3 / 4 3/4 3/4; k k k变大时,近似比则可以任意接近 1 − 1 / e 1-1/e 1−1/e。

作者的整体思路分三步走:
- Counter Example :首先构建worst case “balanced OPT”。在这个case中greedy算法的影响力函数 v a l ( . ) val(.) val(.)几乎是线性的,且每个OPT中的节点的影响力几乎是一样的。在这种情况下,greedy的近似比是 1 − 1 / e 1-1/e 1−1/e;除此之外,greedy的近似比都大于 1 − 1 / e 1-1/e 1−1/e。
- Linearity:在无向图中考虑 v a l ( . ) val(.) val(.)函数的线性情况。这里指的是,无向图中的OPT中的元素必须尽可能的不处在同一个连通分量中: v a l ( O P T ) − v a l ( O P T ∖ o i ) > v a l ( o i ) val(OPT) - val(OPT \setminus {o_i}) > val(o_i) val(OPT)−val(OPT∖oi)>val(oi),即节点 o i o_i oi的增益大于其本身的影响力。这对greedy有很大的影响。
- Technical part:设 S S S为 O P T OPT OPT中前 k / 4 k/4 k/4个种子,考虑greedy选择剩余的种子的情况:作者证明了要么greedy会选择具有较大增益的点,达到 1 − 1 / e + c 1-1/e+c 1−1/e+c的近似;要么就是在balanced form情况下,OPT会导致矛盾。这里矛盾的点在于:在balance form时,greedy在选完前 4 / k 4/k 4/k个种子后,接着应该继续选具有最大增益的点(Lemma 4.2),否则就不会具有比 1 − 1 / e 1-1/e 1−1/e更好的近似比;换句话说,假设greedy不能提供更好的近似比,那么应该选出增益低的节点,但是由于 M ′ M' M′(后续会讲到)中的节点是 5 ϵ 5\epsilon 5ϵ-uniform的,和 S S S在一个连通分量中的概率会很低,因此要选一个 O i ∈ M ′ O_i\in M' Oi∈M′具有低增益是不可能的,因为增益迪就说明 O i O_i Oi和S在同一个连通分量里面。证明的过程用到了一些technical的概率分析,描述了 XYZ \textit{XYZ} XYZ Lemma。
Preliminaries
Notations
| notations | Meaning |
|---|---|
| < G ( V , E ) , U , p , w , k > <G(V,E),U,p,w,k> <G(V,E),U,p,w,k> | An undirected graph |
| U | a valid seed set |
| p p p | he probability in edges |
| w w w | the weight on node |
| k k k | an integer |
| H ( V ′ , E ′ ) H(V',E') H(V′,E′) | an live-edge graph of G G G |
| v a l ( S ∣ T ) val(S|T) val(S∣T) | v a l ( S ∪ T ) − v a l ( T ) val(S \cup T) - val(T) val(S∪T)−val(T) |
| S → T S \rightarrow T S→T | some vertices in S S S in the same component of T T T |
此外,这里作者提供了一个加权图和无权图互相转化的方法。故文章中提到的图都是无权图。
Main results

这也是这篇paper的主要贡献,接下来是定理3.1的证明,也就是文章中具有technical的部分。首先构建lemma 3.1和lemma 3.2,这两个lemma想做的事情是说,当OPT不是特定的"balance"形式的时候,定理3.1是成立的。这里的“balance”其实就是worst case。
Reduction to Balanced Optimal Instances
首先定义了归一化影响力,具体定义如下。这个式子衡量了 X X X中节点的平均影响力和OPT中总体节点影响力的比值。 ρ ( x ) > 1 \rho(x) >1 ρ(x)>1说明 X X X中节点的平均影响力比OPT的节点平均影响力🐮。

给定 ϵ > 0 \epsilon > 0 ϵ>0,我们说一组节点 X X X是 ϵ \epsilon ϵ-uniform 的,若其每个不包含x节点的集合 X X X的元素的normalized influence浮动都很小,即 ( 1 − ϵ ) ≤ ρ ( x ∣ X ∖ x ) ≤ ( 1 + ϵ ) (1-\epsilon) \leq \rho(x \mid X \setminus {x}) \leq (1 + \epsilon) (1−ϵ)≤ρ(x∣X∖x)≤(1+ϵ),那么该组节点的发挥就很稳定,称之为 ϵ \epsilon ϵ-uniform。
X X X是 ϵ \epsilon ϵ-independent的:若每个节点和X中其他节点出现在同一连通分量的概率 P r [ x → X { x } ] ≤ ϵ Pr[x \rightarrow X\ \{x\}] \leq \epsilon Pr[x→X {x}]≤ϵ。
X X X是 ϵ \epsilon ϵ-balanced:同时满足 ϵ \epsilon ϵ-uniform和 ϵ \epsilon ϵ-independent,也就是说这组节点即均匀分布,又发挥稳定( v a l ( . ) val(.) val(.)几乎是线性的)。
这个章节的目的是想说明对于这样的一个 ϵ > 0 \epsilon > 0 ϵ>0,greedy要么可以实现一个 1 − 1 / e + f ( ϵ ) 1-1/e+f(\epsilon) 1−1/e+f(ϵ)的近似,要么OPT就是 ϵ \epsilon ϵ-balanced。

Lemma 3.1说明了greedy算法严格保证了一个大于 1 − 1 / e 1-1/e 1−1/e的近似比。证明如下:


接下来的lemma说明,OPT一定满足下面两个条件之一:1、要么包含了一组 X X X,满足归一化后的X的影响力严格大于1且 v a l ( X ) = Ω ( v a l ( O P T ) ) val(X) = \Omega(val(OPT)) val(X)=Ω(val(OPT)),即 X X X的lower bound是 v a l ( O P T ) val(OPT) val(OPT);2、要么OPT可以根据条件划分为L,H,M。L的划分方法如下:

其实这里 L L L存放了一组点,满足 v a l ( L ) ≤ ϵ ⋅ v a l ( O P T ) val(L) \leq \epsilon \cdot val(OPT) val(L)≤ϵ⋅val(OPT),也就是将 o i o_i oi加入 Z Z Z(不包含 o i o_i oi)带来的收益小于 ( 1 − ϵ ) v a l ( O P T ) k \frac{(1-\epsilon)val(OPT)}{k} k(1−ϵ)val(OPT)的那部分点,这些点至少会有 ϵ ⋅ k \epsilon \cdot k ϵ⋅k个。对于剩下的 k − ϵ ⋅ k k - \epsilon \cdot k k−ϵ⋅k个点,我们将它划分到 X X X中。

这样一来, ρ ( X ) > 1 \rho (X) >1 ρ(X)>1且 v a l ( X ) = Ω ( v a l ( O P T ) ) val(X) = \Omega(val(OPT)) val(X)=Ω(val(OPT))。

若 ∣ L ∣ ≤ ϵ ⋅ k \mid L \mid \leq \epsilon \cdot k ∣L∣≤ϵ⋅k,则不存在 X X X,那么继续划分。对于M和H,划分方法如下:

也就是说,在一个集合 Z = O 1 , . . . , O k Z = {O_1,...,O_k} Z=O1,...,Ok中,L是Z中一系列增益小于 ( 1 − ϵ ) v a l ( O P T ) k \frac{(1-\epsilon)val(OPT)}{k} k(1−ϵ)val(OPT)的节点,那么对于Z中剩下的点,选出前 j j j个连续增益最大的点 { O δ ( 1 ) , . . . , O δ ( j ) } \{O_{\delta(1)},...,O_{\delta(j)}\} {Oδ(1),...,Oδ(j)},若这些点的影响力大于 ϵ 2 v a l ( O P T ) \epsilon^2val(OPT) ϵ2val(OPT),则将其划分为X;否则为 H H H,剩下的点为 M M M。这波操作下来, L , H , M L,H,M L,H,M中的点都不会有normalized influence大于1的情况,也就是说,greedy在这种情况下不会出现比 1 − 1 / e 1-1/e 1−1/e好的近似比。根据划分的方法,满足lemma3.2中的条件:M是 ϵ \epsilon ϵ-uniform的。
证明如下:

接下来肯定是证明 ϵ \epsilon ϵ-independent了。但这里只证明 M M M中的部分。对于M,有:

也就是说, M ′ M' M′存在于 M M M中,且大小至少为 ∣ M ∣ − ϵ k \mid M\mid-\epsilon k ∣M∣−ϵk,且 M ′ M' M′中每个点 O i O_i Oi在 M ′ M' M′的连通分量中的概率最多为 5 ϵ 5\epsilon 5ϵ。这个证明暂且skip,没看懂。
Proving Theorem 3.1 for Balanced Optimal Instances

现在的情况是OPT被分成上面的样子了,这里 M ′ M' M′满足 5 ϵ 5\epsilon 5ϵ-independent和 ϵ \epsilon ϵ-uniform。按照之前的证明思路,若是有一个集合满足 ϵ \epsilon ϵ-balanced,那么该集合上的 v a l ( . ) 就是几乎就是线性的。接下来的证明策略如下。首先证明,给定 val(.)就是几乎就是线性的。接下来的证明策略如下。首先证明,给定 val(.)就是几乎就是线性的。接下来的证明策略如下。首先证明,给定S = {g_1,g_2,…,g_{k/4}}$,如果贪婪算法没有达到比 1 − 1 / e 1−1/e 1−1/e更好的近似, 那么每个 O i ∈ M ′ O_i\in M' Oi∈M′的边际影响一定不能太大(lemma 3.4),否则就会有greedy超过 1 − 1 / e 1-1/e 1−1/e的情况发生。


Lemma3.4描述了greedy选完前 k / 4 k/4 k/4之后依然还能选出增益大于 4 / 5 v a l ( O P T ) k 4/5 \frac{val(OPT)}{k} 4/5kval(OPT)的情况。接下来的Lemma 3.5会考虑矛盾的情况:当 M ′ M' M′中还存在更低的uniform集合。

L e m m a 3.4 Lemma 3.4 Lemma3.4和 L e m m a 3.5 Lemma 3.5 Lemma3.5似乎是矛盾的,因为粗略地说,当 O i O_i Oi和 S S S在同一连通分量中的概率很大时,给定S,加入 O i O_i Oi的边际影响会很小。为了正式的说明这一点,我们必须为连通分量的大小和连接性事件之间的相关性建立界限;这个界限在XYZ引理(引理3.6)中被定义。

这里作者给出了两个定义:

对于一个点 j ∈ E i j \in E_i j∈Ei,definition 1说 j j j对于 O i ∈ M ′ ′ O_i \in M'' Oi∈M′′是"exclusive":当 j j j在 M ′ ′ M'' M′′、 S S S的连通分量中,不在 H H H的连通分量中时, j j j被感染的概率依然小;
definition 2说 j j j对于 O i ∈ M ′ ′ O_i \in M'' Oi∈M′′是"good":definition 2想说的是, M ′ ′ M'' M′′和S都影响j的概率并不比 M ′ ′ M'' M′′影响 j j j的概率小多少。
最后,将XYZ引理应用于 M ′ M' M′和S,我们将证明, M ′ ′ M'' M′′中大部分的影响力都是由于 O i O_i Oi影响了一个"exclusive and good" j j j。
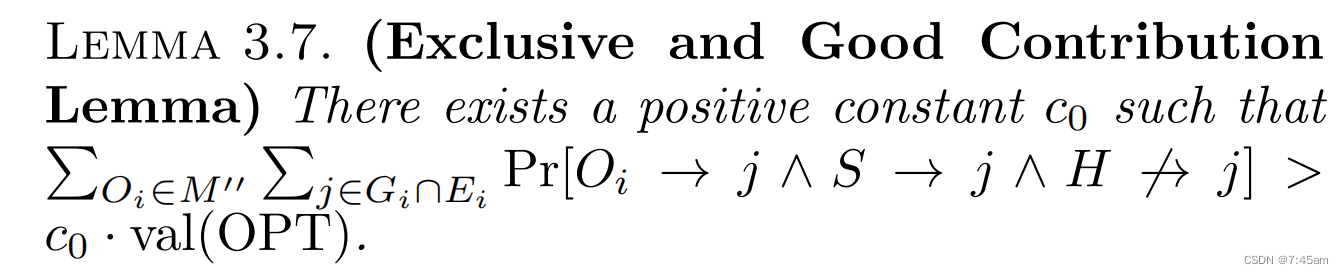
到目前为止,我们集齐了所有的武器,接下来可以证明theorem 3.1了。
这里证明的思路大概如下:先假设theorem 3.1不成立,即 v a l ( G R D ) ≤ ( 1 − 1 / e + c ) v a l ( O P T ) val(GRD)\leq (1-1/e+c)val(OPT) val(GRD)≤(1−1/e+c)val(OPT),那么由lemma 3.1,3.2和3.3可将OPT分解为 L , M ′ , M ′ ′ , H L,M',M'',H L,M′,M′′,H且满足lemma 3.5( ∣ M ′ ′ ∣ ≥ k / 3 a n d P r [ O i → S ] < 14 ϵ |M''| \geq k/3 and Pr[O_i \rightarrow S] < 14 \sqrt{\epsilon} ∣M′′∣≥k/3andPr[Oi→S]<14ϵ for all O i ∈ M ′ ′ O_i \in M'' Oi∈M′′)。通过随后的几个Lemma,作者证明了再这种情况下依然有 v a l ( S ) ≥ c 2 ⋅ 1 δ v a l ( O P T ) val(S) \geq c_2 \cdot \frac{1}{\delta}val(OPT) val(S)≥c2⋅δ1val(OPT)(这里S是GRD的前k个种子, δ = 14 ϵ \delta = 14\sqrt{\epsilon} δ=14ϵ),因此原结论成立。
相关文章:
论文笔记——Influence Maximization in Undirected Networks
Influence Maximization in Undirected Networks ContributionMotivationPreliminariesNotations Main resultsReduction to Balanced Optimal InstancesProving Theorem 3.1 for Balanced Optimal Instances Contribution 好久没发paper笔记了,这篇比较偏理论&…...
Stable Diffusion - SDXL 1.0 全部样式设计与艺术家风格的配置与提示词
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/132072482 来源于 Anna Dittmann 安娜迪特曼,艺术家风格的图像,融合幻想、数字艺术、纹理等样式。 SDXL 是 Stable Diffus…...

Hbase pe 压测 OOM问题解决
说明:本人使用CDH虚拟机搭建了Hbase集群,但是在压测的时发现线程多个的时候直接回OOM,记录一下 执行命令 hbase pe --nomapred --oneContrue --tablerw_test_1 --rows1000 --valueSize100 --compressSNAPPY --presplit10 --autoFlushtrue randomWrite …...

问题解决——datagrip远程连接虚拟机中ubuntu的mysql失败
问题解决——datagrid远程连接虚拟机中ubuntu的mysql失败 情况:datagrip远程win11系统下虚拟机里的ubuntu20.04的mysql,连接失败。 1 如果是防火墙没开放3306端口,则需要开放:linux 3306端口无法连接 无法通过防火墙的解决办法 …...

【晚风摇叶之随机密码生成器】随机生成密码
需求:想要生成位数不低于16的随机密码,而且要包含大小写字母,数字,特殊字符四类 用别人的在线生成器,生成的密码有个别没有数字或者特殊字符,验证方式就是,生成几个长度是4的密码,看…...

Spring Cache
什么是Spring Cache? Spring Cache是Spring框架的一个模块,它提供了对应用程序方法级别的缓存支持。通过使用Spring Cache,您可以在方法的结果被计算后,将其缓存起来,从而避免相同输入导致的重复计算。 Spring Cache…...
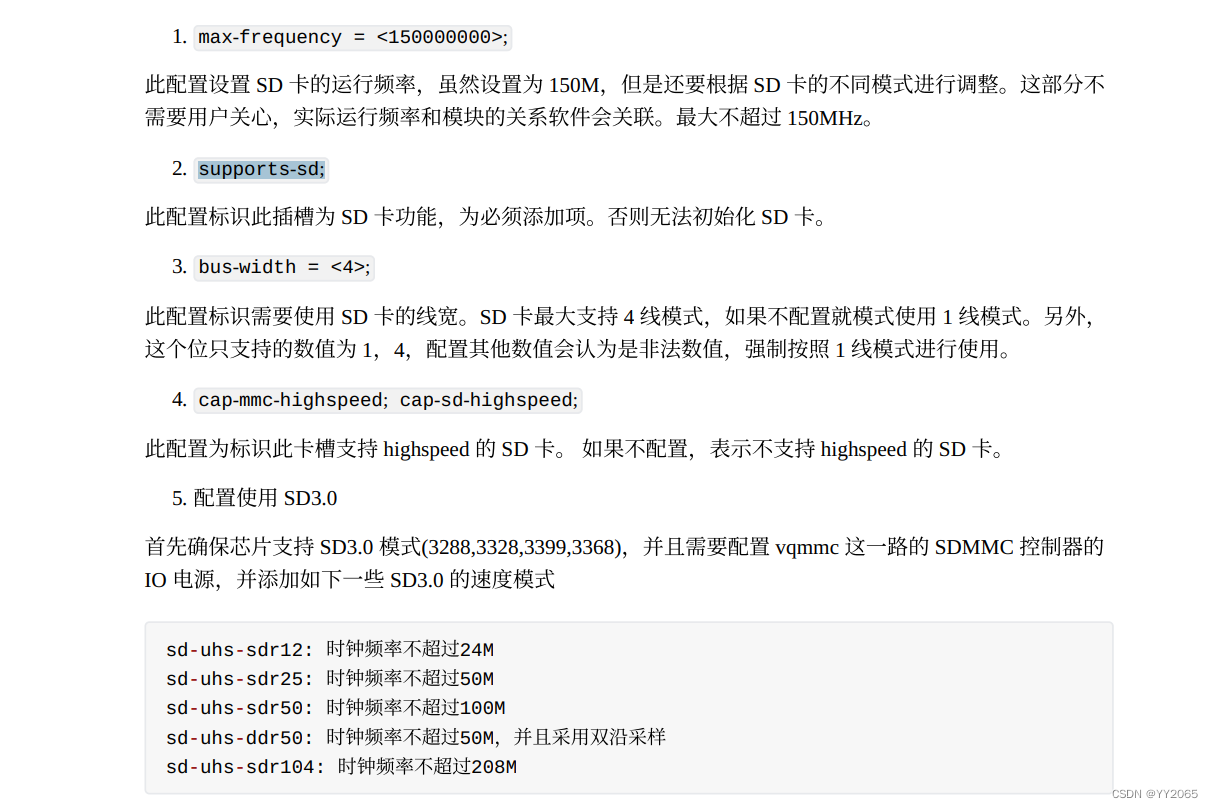
em3288 linux_4.19 sd卡调试
默认配置,根据实际配置即可。...

前端vue uni-app cc-countdown倒计时组件
随着技术的不断发展,传统的开发方式使得系统的复杂度越来越高。在传统开发过程中,一个小小的改动或者一个小功能的增加可能会导致整体逻辑的修改,造成牵一发而动全身的情况。为了解决这个问题,我们采用了组件化的开发模式。通过组…...
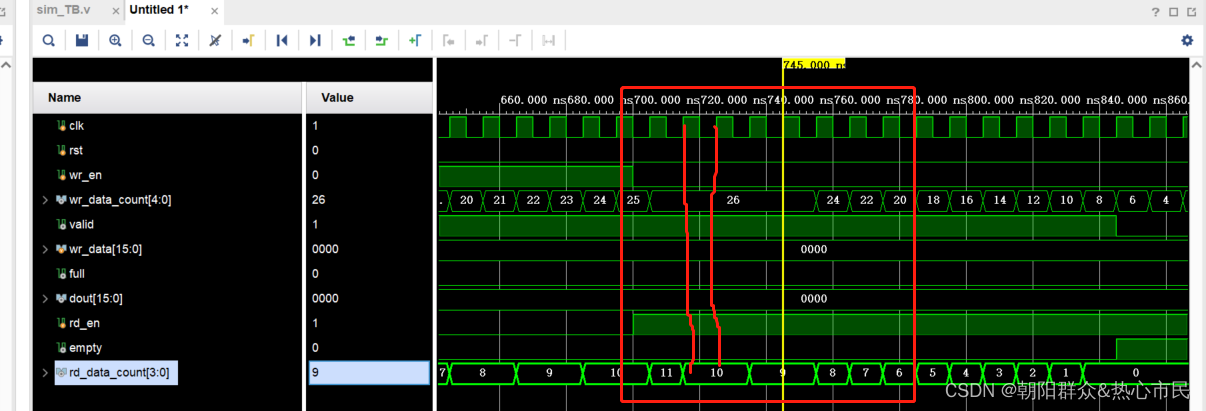
fifo读写的数据个数
fifo IP核设置读写个数 如果不勾选精确值,则统计的当前写入和待读出的数据为估计值,可能会相差2个左右。且fifo设计的wr_data_count. wr_data_count:当前的fifo中剩余已经写入的数据。 rd_data_count:当前的fifo中剩余可以读出…...

Java之Map接口
文章目录 简述Map中key-value特点 Map接口的常用方法Map的主要实现类:HashMapHashMap概述 Map实现类之二:LinkedHashMapMap实现类之三:TreeMapMap实现类之四:Hashtable(古老实现类)Map实现类之五࿱…...
,但是pycharm的terminal中无法使用。)
windows系统中的命令行可以用python,pip等命令(已在系统中添加过python环境变量),但是pycharm的terminal中无法使用。
如果你已经在Windows系统中添加了Python环境变量,那么在命令行中使用python和pip命令应该是没有问题的。但是在PyCharm的Terminal中无法使用这些命令,可能是因为PyCharm的Terminal使用的是自己的虚拟环境,而不是系统环境。 你可以尝试在PyCh…...

编译 OneFlow 模型
本篇文章译自英文文档 Compile OneFlow Models tvm 0.14.dev0 documentation 作者是 BBuf (Xiaoyu Zhang) GitHub 更多 TVM 中文文档可访问 →Apache TVM 是一个端到端的深度学习编译框架,适用于 CPU、GPU 和各种机器学习加速芯片。 | Apache TVM 中文站 本文介…...
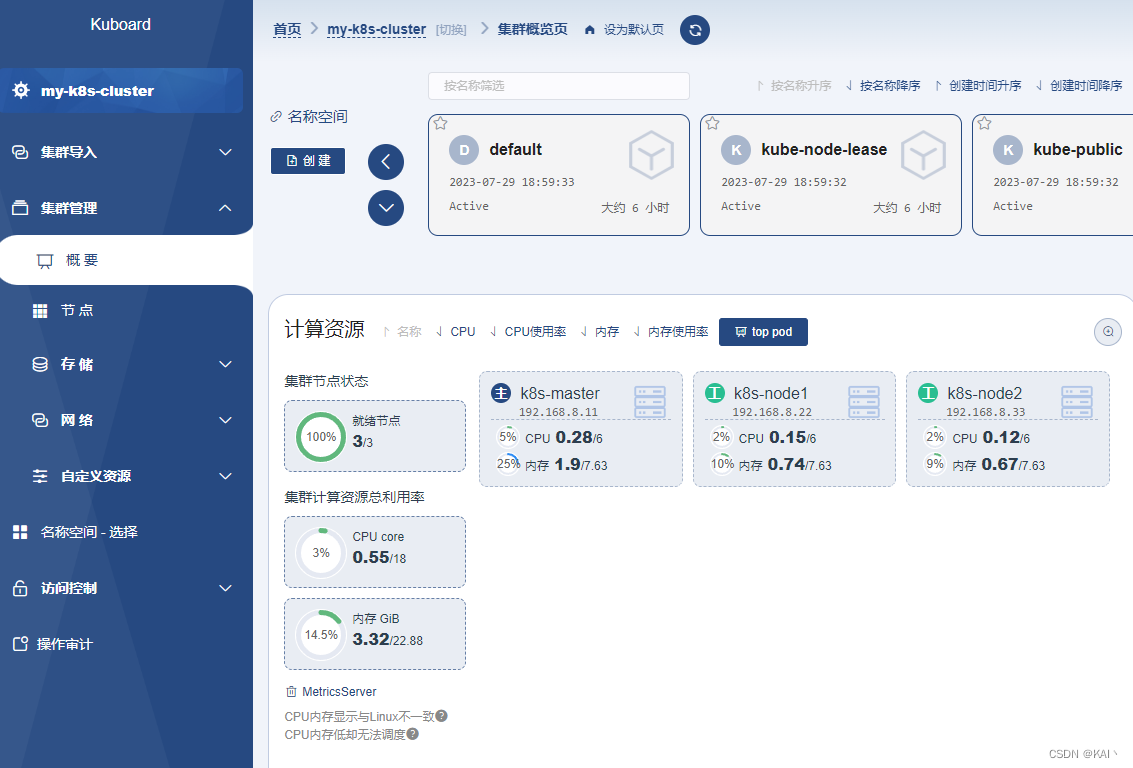
【kubernetes】k8s单master集群环境搭建及kuboard部署
k8s入门学习环境搭建 学习于许大仙: https://www.yuque.com/fairy-era k8s官网 https://kubernetes.io/ kuboard官网 https://kuboard.cn/ 基于k8s 1.21.10版本 前置环境准备 一主两从,三台虚拟机 CPU内存硬盘角色主机名IPhostname操作系统4C16G50Gmasterk8s-mast…...
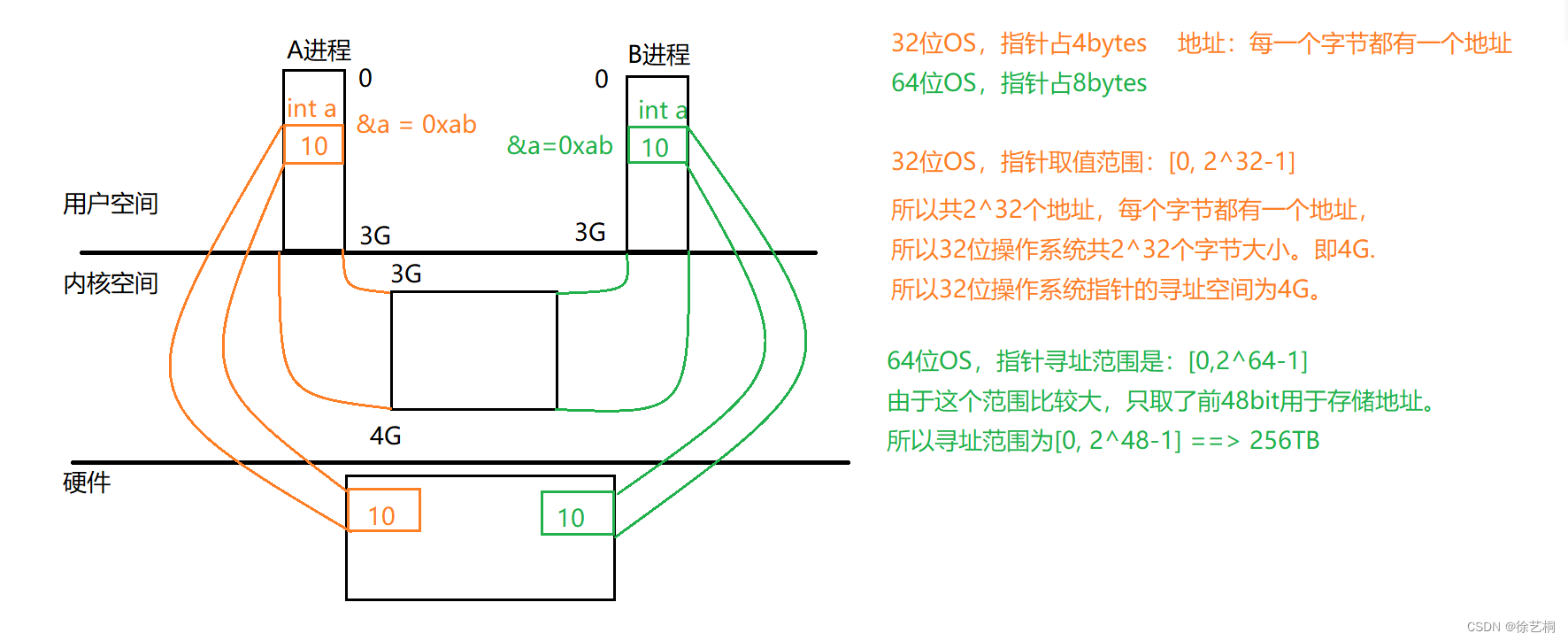
0802|IO进程线程 day5 进程概念
一、进程的基础 1.1 什么是进程 1)进程是程序的一次执行过程 程序:是静态的,它是存储在外存上的可执行二进制文件;进程:动态的概念,它是程序的一次执行过程,包括了进程的创建,调度、…...
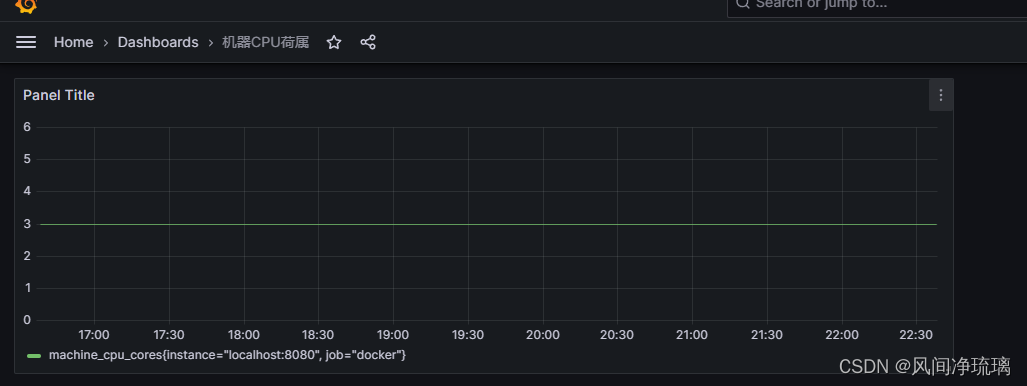
4 Promethues监控主机和容器
目录 目录 1. 监控节点 1.1 安装Node exporter 解压包 拷贝至目标目录 查看版本 1.2 配置Node exporter 1.3 配置textfile收集器 1.4 启动systemd收集器 1.5 基于Docker节点启动node_exporter 1.6 抓取Node Exporter 1.7 过滤收集器 2. 监控Docker容器 2.1 运行cAdviso…...
亚马逊买家账号ip关联怎么处理
对于亚马逊买家账号,同样需要注意IP关联问题。在亚马逊的眼中,如果多个买家账号共享相同的IP地址,可能会被视为潜在的操纵、违规或滥用行为。这种情况可能导致账号受到限制或处罚。 处理亚马逊买家账号IP关联问题,建议采取以下步骤…...
NO4 实验四:生成Web工程
1、说明 使用 mvn archetype:generate 命令生成 Web 工程时,需要使用一个专门的 archetype。这个专门生成 Web 工程骨架的 archetype 可以参照官网看到它的用法: 2、操作 注意:如果在上一个工程的目录下执行 mvn archetype&…...
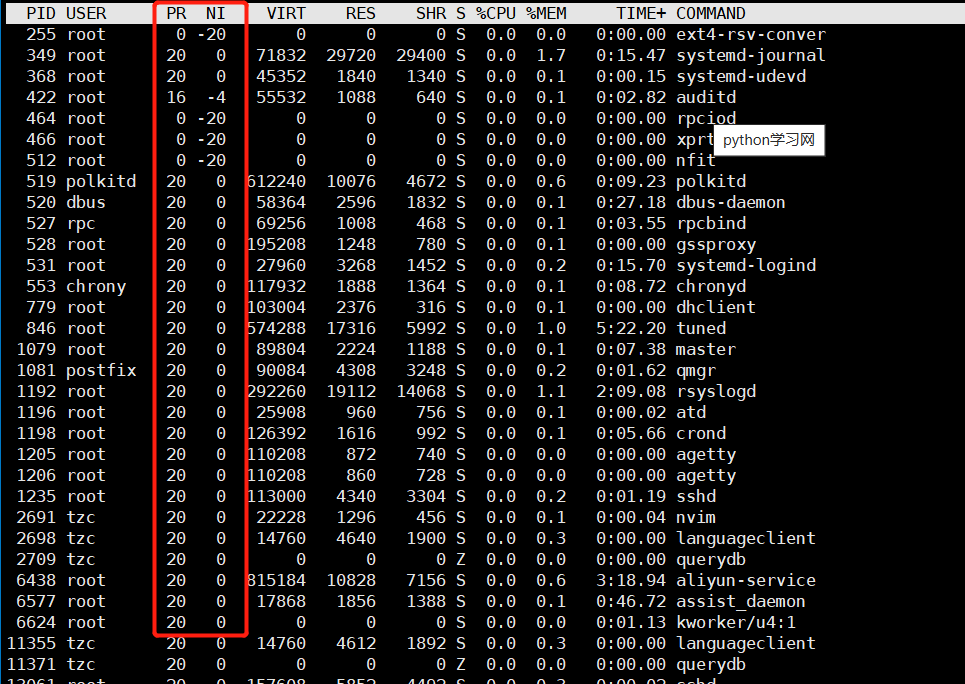
【linux】进程
文章目录 前言一、概念基本概念进程-PCBtask_structtask_struct内容分类 二、查看和创建进程查看进程PID创建进程 三、进程状态五、僵尸进程和孤儿进程僵尸进程孤儿进程获取进程退出码 四、进程优先级基本概念查看系统进程PRI and NI用top命令更改已存在进程的nice 前言 我们常…...

电商高并发设计之SpringBoot整合Redis实现布隆过滤器
文章目录 问题背景前言布隆过滤器原理使用场景基础中间件搭建如何实现布隆过滤器引入依赖注入RedisTemplate布隆过滤器核心代码Redis操作布隆过滤器验证 总结 问题背景 研究布隆过滤器的实现方式以及使用场景 前言 本篇的代码都是参考SpringBootRedis布隆过滤器防恶意流量击穿缓…...

SpringBoot第25讲:SpringBoot集成MySQL - MyBatis 注解方式
SpringBoot第25讲:SpringBoot集成MySQL - MyBatis 注解方式 本文是SpringBoot第25讲,上文主要介绍了Spring集成MyBatis访问MySQL,采用的是XML配置方式;我们知道除了XML配置方式,MyBatis还支持注解方式。本文主要介绍Sp…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
