排序进行曲-v1.0
排序
排序是将一组数据按照一定的规则进行排列的过程。在计算机科学中,排序是一
种常见的算法问题,通常用于对数据进行整理、查找、统计等操作。
概念解读
基本概念
排序算法:排序算法是实现数据排序的具体方法。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等。每个排序算法都有其特定的时间复杂度和空间复杂度,适用于不同规模和特点的数据集合。排序稳定性:排序稳定性是指排序算法在排序过程中是否能够保持相等元素的相对顺序不变。稳定的排序算法可以确保相等元素的顺序不会发生变化,而不稳定的排序算法则无法保证。例如,对于序列[3a, 2, 3b, 1],如果排序算法是稳定的,那么排序后的结果应该是[1, 2, 3a, 3b],否则可能是[1, 2, 3b, 3a]内部排序和外部排序:内部排序是指在内存中对数据进行排序,而外部排序是指在外部存储介质(如硬盘)上对数据进行排序。内部排序通常适用于数据规模较小的情况,可以直接将数据加载到内存中进行排序;而外部排序适用于数据规模较大的情况,需要借助外部存储介质进行分段排序。排序的时间复杂度和空间复杂度:排序算法的时间复杂度是指排序算法执行所需的时间,通常以大O表示法表示。不同的排序算法具有不同的时间复杂度,从O(n^2)到O(nlogn)不等。排序算法的空间复杂度是指排序算法执行所需的额外空间,包括辅助数组、栈空间等。空间复杂度也是根据算法的特点而不同。排序的稳定性和效率的权衡:在选择排序算法时,需要考虑排序的稳定性和效率之间的权衡。稳定的排序算法可以确保相等元素的相对顺序不变,但可能牺牲一定的效率;而不稳定的排序算法可能具有更高的效率,但无法保证相等元素的顺序。具体选择哪种排序算法取决于具体的应用场景和需求。
分类
内部排序和外部排序
内部排序:所有待排序的数据可以一次性加载到内存中进行排序,常见的内部排序算法有冒泡排序、插入排序、选择排序、快速排序、归并排序等。外部排序:待排序的数据量太大,无法一次性加载到内存中进行排序,需要利用外部存储进行排序,常见的外部排序算法有多路归并排序、败者树排序等。
内部排序精讲
冒泡排序是一种简单的排序算法,它通过多次比较相邻的元素,并交换位置,从而将最大(或最小)的元素逐渐“冒泡”到正确的位置。插入排序是一种通过构建有序序列,对未排序数据逐个进行插入的排序算法。在插入排序中,将第一个元素视为已排序序列,然后将后续元素依次插入到已排序序列的正确位置。选择排序是一种简单直观的排序算法,它通过每次从未排序序列中选择最小(或最大)的元素,将其放置到已排序序列的末尾。快速排序是一种高效的排序算法,它采用分治的策略,将问题分解为多个子问题,并通过递归的方式解决。快速排序的基本思想是选择一个基准元素,将序列分为两个子序列,其中一个子序列的元素都小于基准元素,另一个子序列的元素都大于基准元素,然后对子序列进行递归排序。归并排序是一种稳定的排序算法,它采用分治的策略,将问题分解为多个子问题,并通过递归的方式解决。归并排序的基本思想是将序列分成两个子序列,分别进行排序,然后将两个已排序的子序列合并成一个有序序列。
外部排序精讲
多路归并排序的过程
1、将待排序的序列分成多个子序列,每个子序列都是有序的。2、创建一个辅助数组,用于存储合并后的有序序列。3、依次比较每个子序列的第一个元素,选择最小的元素放入辅助数组中,并将该元素所在子序列的指针后移一位。4、重复步骤3,直到所有子序列都为空。5、将辅助数组中的元素复制回原始序列。败者树排序过程
1、初始化败者树:首先,我们需要创建一个败者树的数据结构。败者树是一棵完全二叉树,每个节点表示一个参与排序的数据源。在初始化时,所有节点的值都设置为正无穷大,表示初始状态下的败者。2、建立初始归并段:接下来,我们从每个数据源中读取一个元素,构成初始的归并段。归并段是一个有序的数据序列,每个数据源对应一个归并段。3、比较并选择胜者:对于每个归并段,我们需要比较归并段中的元素,并选择其中的胜者。胜者是指归并段中最小的元素。在比较过程中,我们将败者树中对应节点的值与归并段中的元素进行比较,如果归并段中的元素较小,则将其作为胜者,并将其索引保存在败者树的对应节点中。4、重建败者树:在选择胜者后,我们需要根据新的胜者重新调整败者树。具体操作是将新的胜者与其父节点进行比较,如果新的胜者较小,则将其与父节点交换位置,并继续向上调整,直到达到根节点。5、输出胜者:重复步骤3和步骤4,直到所有归并段中的元素都被选择为胜者。此时,败者树的根节点中保存的就是最小的元素。我们将该胜者输出,并从对应归并段中读取下一个元素,继续比较和选择胜者。6、归并段更新:当一个归并段中的元素被输出后,我们需要从对应的数据源中读取一个新的元素来更新该归并段。如果数据源已经读取完毕,则将其对应节点的值设置为正无穷大,表示该数据源已经没有更多的元素可供选择。7、重复步骤3到步骤6,直到所有数据源中的元素都被输出。
比较排序和非比较排序
比较排序:通过比较待排序元素之间的大小关系来进行排序,常见的比较排序算法有插入排序、选择排序、冒泡排序、快速排序、归并排序、堆排序等。非比较排序:不通过比较待排序元素之间的大小关系来进行排序,常见的非比较排序算法有计数排序、桶排序、基数排序等。
稳定排序和不稳定排序
稳定排序:如果待排序的序列中存在相等的元素,经过排序后,相等元素之间的相对顺序不发生变化,常见的稳定排序算法有插入排序、归并排序、冒泡排序等。不稳定排序:如果待排序的序列中存在相等的元素,经过排序后,相等元素之间的相对顺序可能发生变化,常见的不稳定排序算法有选择排序、快速排序、希尔排序、堆排序等。
内排序算法的时间复杂度
最好情况时间复杂度:表示待排序序列已经有序时的时间复杂度。最坏情况时间复杂度:表示待排序序列逆序时的时间复杂度。平均情况时间复杂度:表示待排序序列各种可能情况下的时间复杂度。
递归排序和非递归排序
递归排序:通过递归的方式进行排序,如快速排序、归并排序等。
非递归排序:不使用递归的方式进行排序,如插入排序、选择排序、堆排序等。
冒泡排序
冒泡排序是一种简单的排序算法,它重复地走访过要排序的元素,依次比较相邻的两个元素,如果它们的顺序错误就交换它们,直到没有需要交换的元素,排序完成。
步骤
1、从待排序的元素中选择第一个元素作为当前元素。
2、将当前元素与其后面的元素进行比较,如果当前元素大于后面的元素,则交换它们的位置,否则保持不变。
3、将当前元素移动到下一个位置,即将当前元素的索引加1。
4、重复步骤2和步骤3,直到当前元素移动到最后一个位置。
5、重复步骤1到步骤4,直到所有元素都被排序。
冒泡排序的核心思想
通过相邻元素的比较和交换来将最大的元素逐渐移动到最后的位置。每一轮排序都会将待排序序列中最大的元素移动到最后。
时间复杂度
时间复杂度为O(n^2),其中n是待排序序列的长度。最好情况下,待排序序列已经是有序的,只需要进行一轮比较,时间复杂度为O(n)。最坏情况下,待排序序列是逆序的,需要进行n-1轮比较,时间复杂度为O(n^2)。
代码实现
public class BubbleSort {public static void main(String[] args) {int[] arr = {5, 3, 8, 4, 2};bubbleSort(arr);System.out.println("排序结果:");for (int num : arr) {System.out.print(num + " ");}}public static void bubbleSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]和arr[j+1]int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
}
简单选择排序
简单排序,也称为冒泡排序和插入排序,是一种基本的排序算法。它的思想是通过多次比较和交换相邻的元素,将最大(或最小)的元素逐渐“冒泡”(或“插入”)到序列的一端,从而实现排序的目的。
具体步骤
以升序排序为例,简单排序的具体步骤如下1遍历待排序的序列,从第一个元素开始。
2比较当前元素与下一个元素的大小。
3如果当前元素大于下一个元素,交换这两个元素的位置,使较大的元素“冒泡”到序列的末尾。
4继续比较下一个元素,重复步骤2和步骤3,直到遍历到序列的倒数第二个元素。
5重复步骤1至步骤4,直到所有元素都按照升序排列。
时间复杂度
简单排序的时间复杂度为O(n^2),其中n为待排序序列的长度。这是因为在最坏情况下,需要进行n-1次遍历,每次遍历需要比较n-1次并进行相应的交换操作。因此,总的比较和交换次数为(n-1) + (n-2) + ... + 1 = n(n-1)/2,即O(n^2)。
代码实现
public class SelectionSort {public static void selectionSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {int minIndex = i;for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}int temp = arr[minIndex];arr[minIndex] = arr[i];arr[i] = temp;}}public static void main(String[] args) {int[] arr = {64, 25, 12, 22, 11};selectionSort(arr);System.out.println("Sorted array:");for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}}
}
相关文章:

排序进行曲-v1.0
排序 排序是将一组数据按照一定的规则进行排列的过程。在计算机科学中,排序是一 种常见的算法问题,通常用于对数据进行整理、查找、统计等操作。概念解读 基本概念 排序算法:排序算法是实现数据排序的具体方法。常见的排序算法包括冒泡排序…...
算法入门篇——用位运算解决一些问题
目录 1.判断一个数是2的次方数 2.统计一个数,它的二进制数中,1的个数 3.在2*(n-1)个数中,找到只出现一次的那个数 1.判断一个数是2的次方数 这个问题有好几种做法,但是最优雅的解法是用’位运算‘来做。…...
腾讯云-宝塔添加MySQL数据库
1. 数据库菜单 2. 添加数据库 3. 数据库添加成功 4. 上传数据库文件 5. 导入数据库文件 6. 开启数据库权限 7. 添加安全组 (宝塔/腾讯云) 8. Navicat 连接成功...

【雕爷学编程】MicroPython动手做(27)——物联网之掌控板小程序
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...

Mysql删除重复数据通用SQL
在日常开发过程中,可能会出现一些 bug,导致 Mysql 数据库数据重复,需要删除重复数据,这里记录下删除重复数据的通用 SQL ,方便以后需要时查阅 1、写法一 DELETE t1 FROMtbl_name t1 INNER JOIN tbl_name t2 WHEREt1.…...

“快速入门Spring Boot:从零开始构建Web应用程序“
标题:快速入门Spring Boot:从零开始构建Web应用程序 摘要:本文将介绍如何使用Spring Boot从零开始构建一个简单的Web应用程序。我们将学习如何配置和启动Spring Boot应用程序,创建控制器和路由,以及如何使用模板引擎来…...
微信小程序tab加列表demo
一、效果 代码复制即可使用,记得把图标替换成个人工程项目图片。 微信小程序开发经常会遇到各种各样的页面组合,本demo为list列表与tab组合,代码如下: 二、json代码 {"usingComponents": {},"navigationStyle&q…...

深入挖掘地核和地幔之间的相互作用
一本新书介绍了我们在理解地核-地幔相互作用和共同进化方面的重大进展,并展示了提高我们对地球深层过程的洞察力的技术发展。 与地核-地幔共同演化相关的地球深层结构和动力学的图示。图片来源:白石千寻 Editors Vox是 AGU 出版部的博客。 地球深层内部很…...
网络:SecureCRT介绍
1. 使用Tab键补全时出现^I,如下操作...

我的512天创作纪念日
眼馋csdn发的虚拟徽章,所以写此文。个人总结,无技术分享。 机缘 写代码的机缘,在于听说这个挣钱多,坐办公室,凤吹不着,雨淋不着。 而写blog的机缘,则在于是自己的技术的总结,经常是…...

mysql进阶-用户密码的设置和管理
一、修改密码 1.1 修改自己的密码 方式一: 推荐使用 alter user user() identified by 新密码;方式二: set password 新密码;演示 [rootVM-4-6-centos /]# mysql -uzhang3 -pZhangSan123456 mysql: [Warning] Using a password on the command line…...
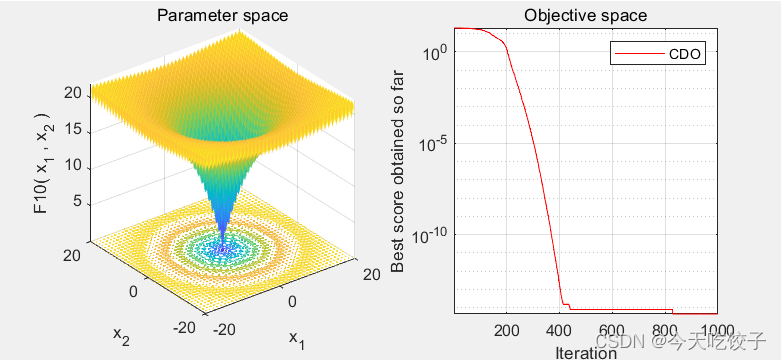
2023年最新智能优化算法之——切诺贝利灾难优化器 (CDO),附MATLAB代码和文献
切诺贝利灾难优化器Chernobyl Disaster Optimizer (CDO)是H. Shehadeh于2023年提出的新型智能优化算法。该方法是受到切尔诺贝利核反应堆堆芯爆炸而来的启发。在CDO方法中,放射性的发生是由于核的不稳定性,核爆炸会发出不同类型的辐射。这些辐射中最常见…...
uniapp跨域解决
uniapp跨域解决 跨域是什么 跨域指的是浏览器不能执行其他网站的脚本,当一个网页去请求另一个域名的资源时,域名、端口、协议任一不同,就会存在跨域。跨域是由浏览器的同源策略造成的,是浏览器对JavaScript施加的安全限制。 报错…...

力扣-94、144、145-前中后序遍历
二叉树遍历方法总结 二叉树的遍历总体上分为深度优先遍历和广度优先遍历。常见的前中后序三种遍历方式就属于深度优先遍历,遍历过程中是顺着一条路径一直遍历到空节点然后向上回溯继续顺着遍历上一个节点的其他方向。层序遍历属于广度优先遍历,先遍历完同…...

什么是线程?为什么需要线程?和进程的区别?
目录 前言 一.线程是什么? 1.1.为什么需要线程 1.2线程的概念 1.3线程和进程的区别 二.线程的生命周期 三.认识多线程 总结 🎁个人主页:tq02的博客_CSDN博客-C语言,Java,Java数据结构领域博主 🎥 本文由 tq02 原创…...
【业务功能篇61】SpringBoot项目流水线 dependencyManagement 标签整改依赖包版本漏洞问题
业务场景:当前我们项目引入了公司自研的一些公共框架组件,比如SSO单点登录jar包,文件上传服务jar包等公共组件,开发新功能,本地验证好之后,部署流水线,报出一些jar包版本的整改漏洞问题…...
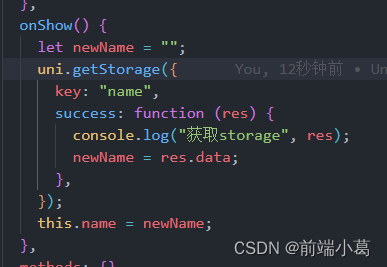
uniapp使用getStorage对属性赋值无效
1正常set(get)storage都是可以正常使用的 2.但对属性进行赋值的时候,却发现this.name并没有发生变化 3. 在里面打印this发现,在set*getStorage中并不能拿到this. 4.优化代码 这样就可以给this.name成功赋值...
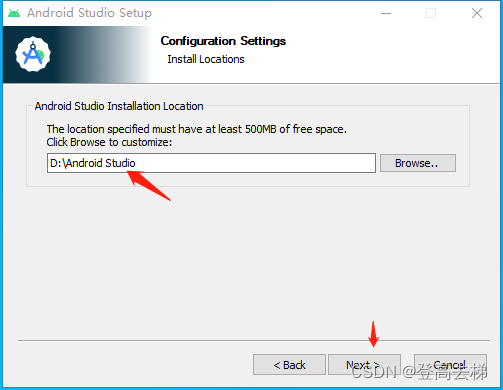
20230802-下载并安装android-studio
下载 android-studio 安装包 https://developer.android.google.cn/studio/ 安装android-studio 双击安装包 D:\Android Studio...
)
python 第九章 —— GUI界面开发(tkinter详解)
文章目录 前言一、GUI与CLI对比二、GUI原理三、tkinter基本使用1.主窗口2.控件(1)button(2)布局(3)Frame(以微信布局为例)(4)Label(5)Entry(6)Text(7)Checkbutton(8)Radiobutton(9)Listbox(10)Scrollbar(11)Canvas...

线段树合并例题
https://www.luogu.com.cn/problem/P3224 1. 永无乡 题意: 给 n 个岛屿,每个岛有一个标号,初始修有 m 条路,有两个操作,操作1 为 给两个岛屿之间修路,操作2为求出 所有能从当前岛屿到达的岛 中标号第k小的…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
