线段树合并例题
https://www.luogu.com.cn/problem/P3224
1. 永无乡
题意:
给 n 个岛屿,每个岛有一个标号,初始修有 m 条路,有两个操作,操作1 为 给两个岛屿之间修路,操作2为求出 所有能从当前岛屿到达的岛 中标号第k小的岛
思路:
求标号第k小的岛,我们考虑使用权值线段树,通过线段树上二分查找第k小,对于多个岛屿,我们考虑动态开点建 n 棵线段树,对于岛屿修路的操作 使用并查集维护连通块,并利用线段树合并实现岛屿合并
代码:
#include<bits/stdc++.h>
using namespace std;#define int long long
#define mid ((l+r)>>1)const int N=1e5+5;
int rt[N],n,m,num,id[N],f[N];
int ls[60*N],rs[60*N],cnt[60*N];int find(int x){return x==f[x]?x:f[x]=find(f[x]);}int merge(int x,int y,int l,int r){ //线段树合并if(!x)return y;if(!y)return x;if(l==r){cnt[x]+=cnt[y];return x;}ls[x]=merge(ls[x],ls[y],l,mid);rs[x]=merge(rs[x],rs[y],mid+1,r);cnt[x]=cnt[ls[x]]+cnt[rs[x]];return x;
}void upd(int &p,int l,int r,int x){ //建树if(!p)p=++num;if(l==r){cnt[p]=1;return;}if(x<=mid)upd(ls[p],l,mid,x);else upd(rs[p],mid+1,r,x);cnt[p]=cnt[ls[p]]+cnt[rs[p]];
}int q(int p,int l,int r,int k){ //二分查找第k小if(cnt[p]<k)return -1;if(l==r)return l;if(cnt[ls[p]]>=k)return q(ls[p],l,mid,k);return q(rs[p],mid+1,r,k-cnt[ls[p]]);
}void solve(){cin>>n>>m;for(int i=1;i<=n;i++){int x;cin>>x;id[x]=i;upd(rt[i],1,n,x);f[i]=i;}while(m--){int u,v;cin>>u>>v;if(find(u)==find(v))continue;u=find(u),v=find(v);rt[u]=merge(rt[u],rt[v],1,n);f[v]=u;}cin>>m;while(m--){string op;int x,y;cin>>op>>x>>y;if(op=="B"){if(find(x)==find(y))continue;x=find(x),y=find(y);rt[x]=merge(rt[x],rt[y],1,n);f[y]=x;}else{x=find(x);int ans=q(rt[x],1,n,y);if(ans!=-1)ans=id[ans];cout<<ans<<endl;}}return;
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;//cin>>T;while(T--){solve();}return 0;
}2. 雨天的尾巴
https://www.luogu.com.cn/problem/P4556
题意:
给一棵树型村庄,每次给 x到y路径上的村庄发一袋 z 粮食 ,求最后 每个村庄拥有数量最多的粮食种类
思路:
将树看成有根树,取1作为根,每次发放粮食的操作 利用树上差分转化为4次单点发放粮食,直接修改即可,查询数量最多的粮食种类,我们采用 权值线段树 维护每种粮食的数量,建n棵线段树,最后通过 线段树合并+dfs 求出线段树的树上前缀和
代码:
#include<bits/stdc++.h>
using namespace std;#define int long longconst int N=1e5+5;
int head[N],cntt=0; //建图
struct Edge{int to,next;
}edge[2*N];
void add(int u,int v){edge[++cntt].to=v;edge[cntt].next=head[u];head[u]=cntt;
}int f[N][30],dis[N],n,t;
void init(){ //lcaqueue<int>q;q.push(1);dis[1]=1;while(!q.empty()){int tmp=q.front();q.pop();for(int i=head[tmp];i;i=edge[i].next){int y=edge[i].to;if(dis[y])continue;dis[y]=dis[tmp]+1;f[y][0]=tmp;q.push(y);for(int j=1;j<=t;j++){f[y][j]=f[f[y][j-1]][j-1];}}}
}
int lca(int u,int v){if(dis[u]>dis[v])swap(u,v);for(int i=t;i>=0;i--){if(dis[f[v][i]]>=dis[u])v=f[v][i];}if(u==v)return u;for(int i=t;i>=0;i--){if(f[u][i]!=f[v][i]){u=f[u][i],v=f[v][i];}}return f[u][0];
}#define mid ((l+r)>>1)int X[N],Y[N],Z[N],rt[N],num=0;
int ls[60*N],rs[60*N],cnt[60*N],pos[60*N];void pushup(int p){if(cnt[ls[p]]>cnt[rs[p]]){cnt[p]=cnt[ls[p]];pos[p]=pos[ls[p]];}else if(cnt[rs[p]]>cnt[ls[p]]){cnt[p]=cnt[rs[p]];pos[p]=pos[rs[p]];}else{cnt[p]=cnt[ls[p]];pos[p]=min(pos[ls[p]],pos[rs[p]]);}
}void upd(int &p,int l,int r,int x,int k){if(!p)p=++num;if(l==r){cnt[p]+=k;pos[p]=l;return;}if(x<=mid)upd(ls[p],l,mid,x,k);else upd(rs[p],mid+1,r,x,k);pushup(p);
}int merge(int x,int y,int l,int r){if(!x)return y;if(!y)return x;if(l==r){cnt[x]+=cnt[y];pos[x]=l;return x;}ls[x]=merge(ls[x],ls[y],l,mid);rs[x]=merge(rs[x],rs[y],mid+1,r);pushup(x);return x;
}int ans[N],mx;
void dfs(int x,int ff){for(int i=head[x];i;i=edge[i].next){int y=edge[i].to;if(y==ff)continue;dfs(y,x);rt[x]=merge(rt[x],rt[y],1,mx);}if(cnt[rt[x]])ans[x]=pos[rt[x]];
}void solve(){int m;cin>>n>>m;t=log2(n);for(int i=1;i<n;i++){int u,v;cin>>u>>v;add(u,v);add(v,u);}init();for(int i=1;i<=m;i++){cin>>X[i]>>Y[i]>>Z[i];mx=max(mx,Z[i]);}for(int i=1;i<=m;i++){upd(rt[X[i]],1,mx,Z[i],1);upd(rt[Y[i]],1,mx,Z[i],1);upd(rt[lca(X[i],Y[i])],1,mx,Z[i],-1);if(f[lca(X[i],Y[i])][0])upd(rt[f[lca(X[i],Y[i])][0]],1,mx,Z[i],-1);}dfs(1,1);for(int i=1;i<=n;i++){cout<<ans[i]<<endl;}return;
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;while(T--){solve();}return 0;
}相关文章:

线段树合并例题
https://www.luogu.com.cn/problem/P3224 1. 永无乡 题意: 给 n 个岛屿,每个岛有一个标号,初始修有 m 条路,有两个操作,操作1 为 给两个岛屿之间修路,操作2为求出 所有能从当前岛屿到达的岛 中标号第k小的…...
Stable Diffusion 硬核生存指南:WebUI 中的 VAE
本篇文章聊聊 Stable Diffusion 生态中呼声最高、也是最复杂的开源模型管理图形界面 “stable-diffusion-webui” 中和 VAE 相关的事情。 写在前面 Stable Diffusion 生态中有一个很重要的项目,它对于 SD 生态繁荣做出的贡献可以说居功至伟,自去年八月…...
)
vue项目 前端加前缀(包括页面及静态资源)
具体步骤 Vue 中配置 (1)更改router模式,添加前缀 位置:router文件夹下面的index.js const router new Router({base: /nhtjfx/, // 路由前缀mode: history, // 采用history模式URL的路径才跟配置的对应上,不然UR…...
使用文心一言等智能工具指数级提升嵌入式/物联网(M5Atom/ESP32)和机器人操作系统(ROS1/ROS2)学习研究和开发效率
以M5AtomS3为例,博客撰写效率提升10倍以上: 0. Linux环境Arduino IDE中配置ATOM S3_zhangrelay的博客-CSDN博客 1. M5ATOMS3基础01按键_zhangrelay的博客-CSDN博客 2. M5ATOMS3基础02传感器MPU6886_zhangrelay的博客-CSDN博客 3. M5ATOMS3基础03给RO…...

【Rust 基础篇】Rust动态大小类型:理解动态大小类型与编写安全的代码
导言 Rust是一种以安全性和高效性著称的系统级编程语言,其设计哲学是在不损失性能的前提下,保障代码的内存安全和线程安全。在Rust中,动态大小类型(DST)是一种特殊的类型,它的大小在编译时无法确定&#x…...

【Python】使用nuitka打包Python程序为EXE可执行程序
1.说明 写好的Python程序如果想要拿到其他电脑上运行,那还得安装一下Python环境和各种库,这是比较麻烦的,所以有必要把它打包成一个可执行的exe文件。可以打包exe的库有好多个,比如说pyinstaller、cx_Freeze等。 pyinstaller打包…...
背景图片及精灵图
.picture {width: 48px;height: 48px;background-image: url(../images/精灵图-侧边功能.png); }为一个有宽高的div设置了背景图片,背景图片只作用在div的content区域内,不作用在padding和border上。 知识点: 背景图使用精灵图(…...
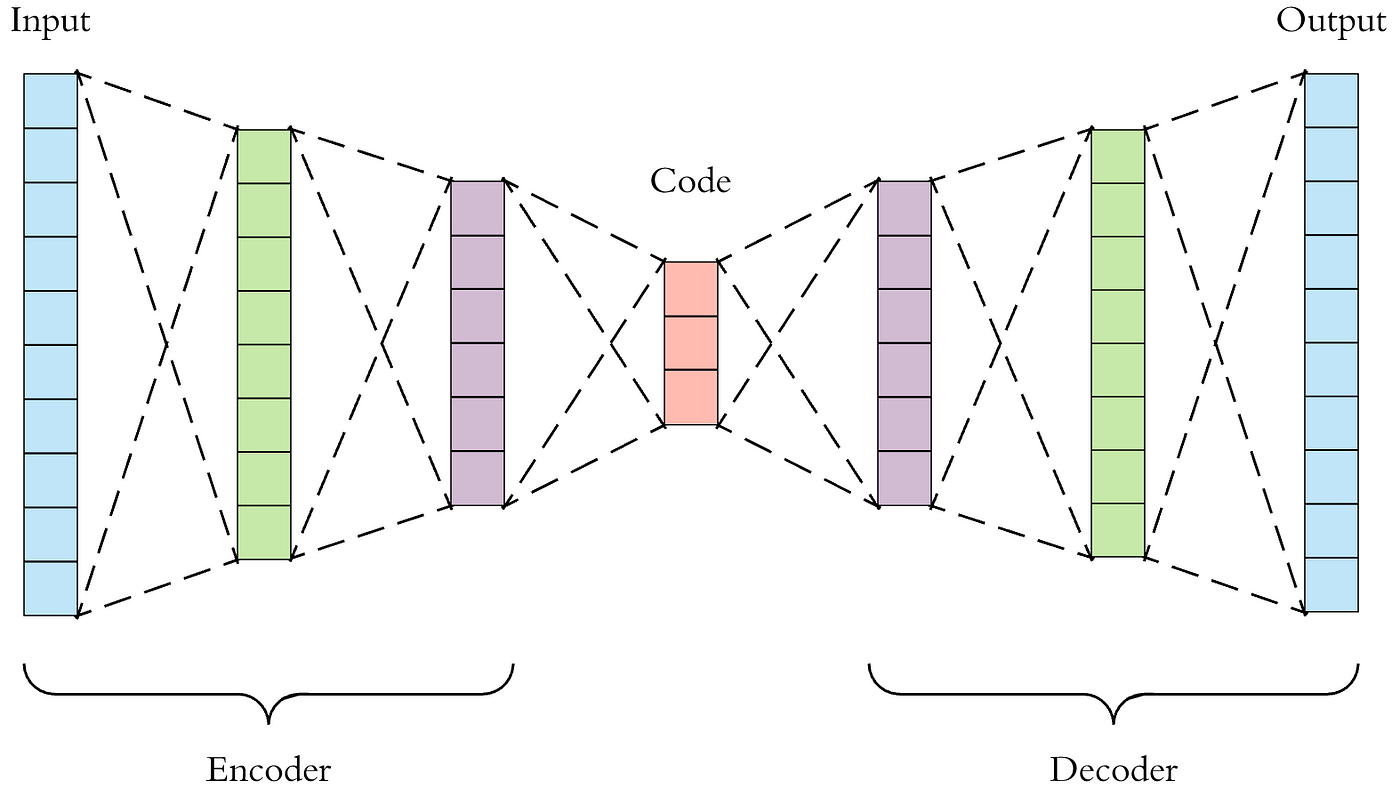
简要介绍 | 生成模型的演进:从自编码器(AE)到变分自编码器(VAE)和生成对抗网络(GAN),再到扩散模型
注1:本文系“简要介绍”系列之一,仅从概念上对生成模型(包括AE, VAE, GAN,以及扩散模型)进行非常简要的介绍,不适合用于深入和详细的了解。 生成模型的演进:从自编码器(AE)到变分自编码器(VAE)和生成对抗网络(GAN),再到扩散模型 一、背景介绍 生成模型在机器学习领域…...
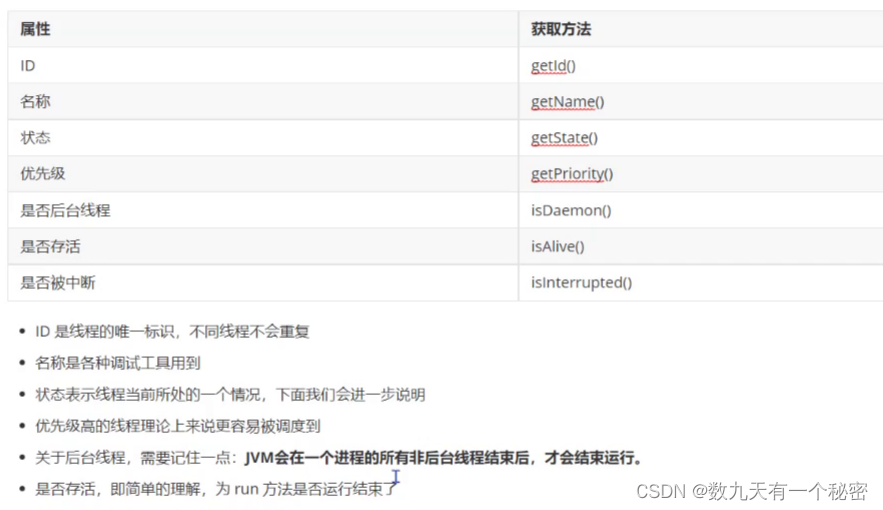
8.2Thread类的常见属性
1. 2.前台线程和后台线程 前台线程:影响进程结束(如果前台线程没有执行完,进程不结束). 后台线程(守护线程):不影响线程结束. 创建线程默认是前台线程. 修改成后台线程:thread.setDaetrue);...

博客摘录「 mvvm框架工作原理及优缺」2023年7月31日
mvvm 的核心是数据劫持、数据代理、数据编译和"发布订阅模式"。 1、数据劫持——就是给对象属性添加get,set钩子函数。 ● 1、观察对象,给对象增加 Object.defineProperty ● 2、vue的特点就是新增不存在的属性不会给该属性添加 get 、 set 钩子函数。…...
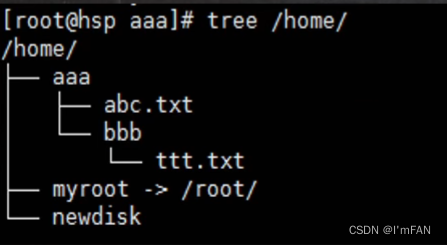
第12章 Linux 实操篇-Linux磁盘分区、挂载
12.1 Linux 分区 12.1.1 原理介绍 (1) Linux来说无论有几个分区,分给哪一目录使用,它归根结底就只有一个根目录,一个独立且唯一的文件结构, Linux中每个分区都是用来组成整个文件系统的一部分。 (2) Linux采用了一种叫“载入”的处理方法,…...

使用express搭建后端服务
目录 1 创建工程目录2 初始化3 安装express依赖4 启动服务5 访问服务总结 上一篇我们利用TDesign搭建了前端服务,现在的开发讲究一个前后端分离,后端的话需要单独搭建服务。后端服务的技术栈还挺多,有java、php、python、nodejs等。在众多的技…...
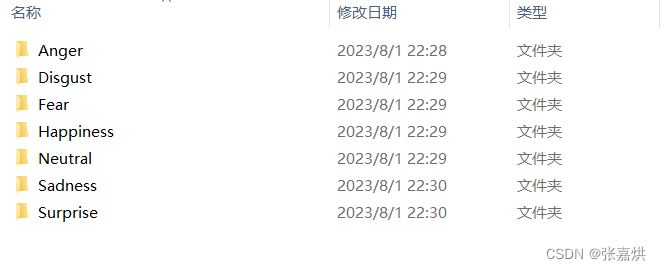
深度学习——划分自定义数据集
深度学习——划分自定义数据集 以人脸表情数据集raf_db为例,初始目录如下: 需要经过处理后返回 train_images, train_label, val_images, val_label 定义 read_split_data(root: str, val_rate: float 0.2) 方法来解决,代码如下:…...
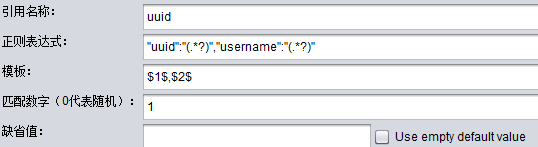
Jmeter性能测试之正则表达式提取器
目录 前言 1. Jmeter正则表达式提取器 2. 入门实例 3. 进阶实例 前言 Jmeter正则表达式提取器属于Jmeter后置处理器(post processors)的一种,用于将取样器请求到的结果以正则表达式的方式读取出来。 1. Jmeter正则表达式提取器 1. 作用…...
)
浅谈Kubernetes中Service网络实现(服务发现)
目录 CoreDNS(Kube-DNS) Kube-proxy kube-proxy的三种实现模式 iptables模式 IPVS模式 之前的文章介绍了Kubernetes中基于service实现了集群内部的网络通信,这篇文章详细聊一下Kubernetes中的Service网络本身又是如何实现的。...

【重造轮子】golang实现可重入锁
造个可重入锁的轮子 介绍目标 正文sync.Mutexsync.Mutex介绍多协程计数器demo多协程计数器加锁 源码剖析Mutex数据结构Lock()加锁核心逻辑 UnLock() 重入锁与可重入锁魔改 sync.Mutex 参考文档 介绍 开新坑啦!! 从这篇文章开始,尝试造轮子&a…...

torch显存分析——对生成模型清除显存
torch显存分析——对生成模型清除显存 1. 问题介绍2. 应对方法 1. 问题介绍 本文主要针对生成场景下,如何方便快捷地清除当前进程占用的显存。文章的重点不止是对显存的管理,还包括怎样灵活的使用自定义组件来控制生成过程。 在之前的文章torch显存分析…...

electron+vue+ts窗口间通信
文章目录 一. 目的二.逻辑分析三. 代码示例 "types/node": "^20.3.1","vitejs/plugin-vue": "^4.1.0","vueuse/electron": "^10.2.1","electron": "^25.2.0","electron-packager":…...
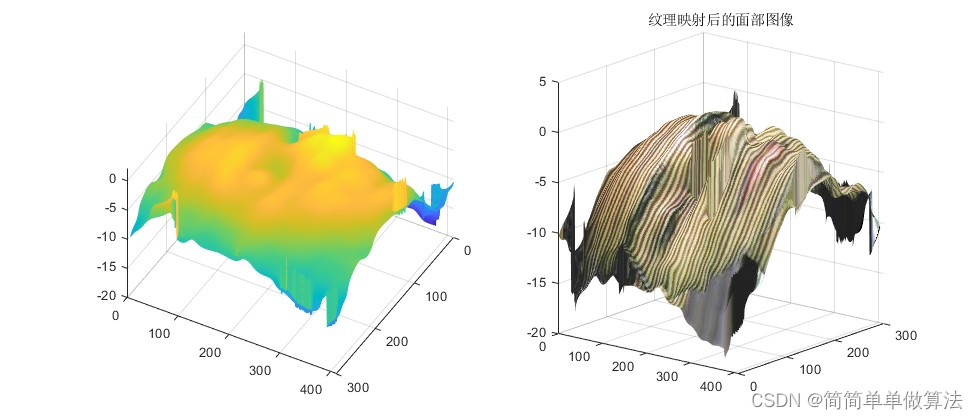
基于Fringe-Projection环形投影技术的人脸三维形状提取算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 .................................................................... figure; imshow(Im…...

如何使用Webman框架实现多语言支持和国际化功能?
如何使用Webman框架实现多语言支持和国际化功能? Webman是一款轻量级的PHP框架,提供了丰富的功能和扩展性,使得开发人员能够更加高效地开发Web应用程序。其中,多语言支持和国际化功能是Web应用程序中非常重要的一项功能ÿ…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
