【物理】带电粒子在磁场和电场中移动的 3D 轨迹研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
带电粒子在磁场和电场中移动的轨迹可以由洛伦兹力定律描述。洛伦兹力定律描述了带电粒子在电场和磁场中所受到的合力,它的表达式为:
F = q(E + v × B)
其中,F 是带电粒子所受到的合力,q 是粒子的电荷量,E 是电场强度,v 是粒子的速度,B 是磁场强度。"×" 表示叉乘。
根据洛伦兹力定律,带电粒子在电场和磁场的共同作用下,其速度和加速度会发生变化,从而导致轨迹的偏转。在三维空间中,粒子的轨迹取决于初始条件,包括粒子的初速度、初始位置以及电场和磁场的性质。
在一个恒定的磁场中,带电粒子将遵循螺旋状轨道,被称为洛伦兹轨道。这是因为磁场对粒子施加一个垂直于速度方向的力,使得粒子不断弯曲向心,形成一个螺旋形轨道。
在存在电场的情况下,电场会对带电粒子产生力,使粒子加速或减速。因此,带电粒子的轨迹将不再是简单的螺旋形状,而是受到电场力的影响而产生偏移。
需要注意的是,粒子的质量、电荷、速度、磁场和电场的特性等因素都会影响轨迹的形状和特征。因此,具体的轨迹方程需要通过数值模拟或解析方法来求解,具体取决于系统的参数和初始条件。
总结起来,带电粒子在磁场和电场中移动时的轨迹是一个复杂的问题,取决于粒子的初始条件以及磁场和电场的性质。通过洛伦兹力定律,可以描述其受到的合力,但具体的轨迹方程需要根据具体情况进一步分析和计算。
使用有限差分法求解由洛仑兹力定律推导出的带电粒子在均匀磁场或均匀电场或交叉磁场和电场中的运动方程。mscript 的图形输出汇总了仿真中使用的参数、
XY 平面中的轨迹以及 3D 轨迹和位移、速度和加速度时间图。
📚2 运行结果
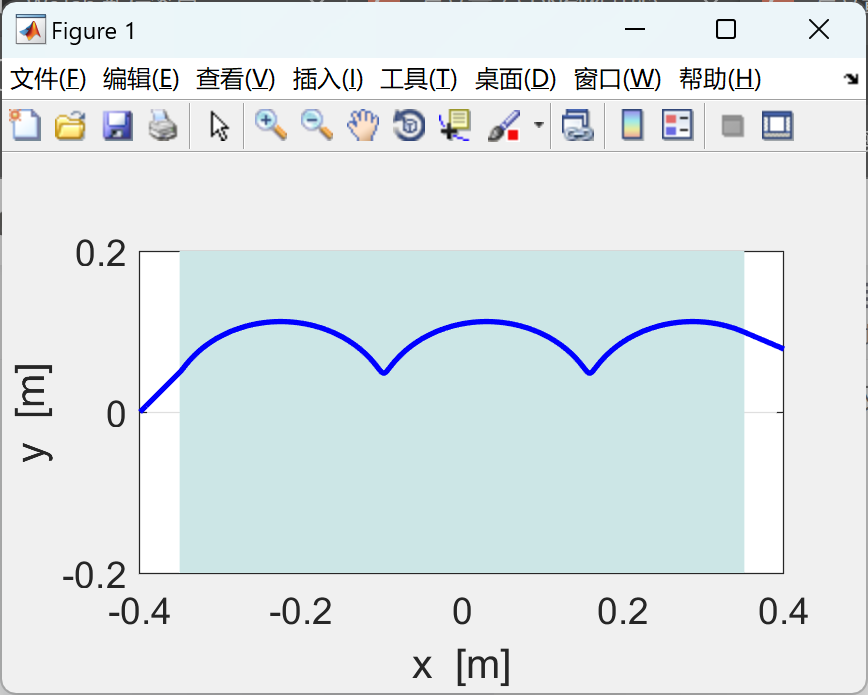
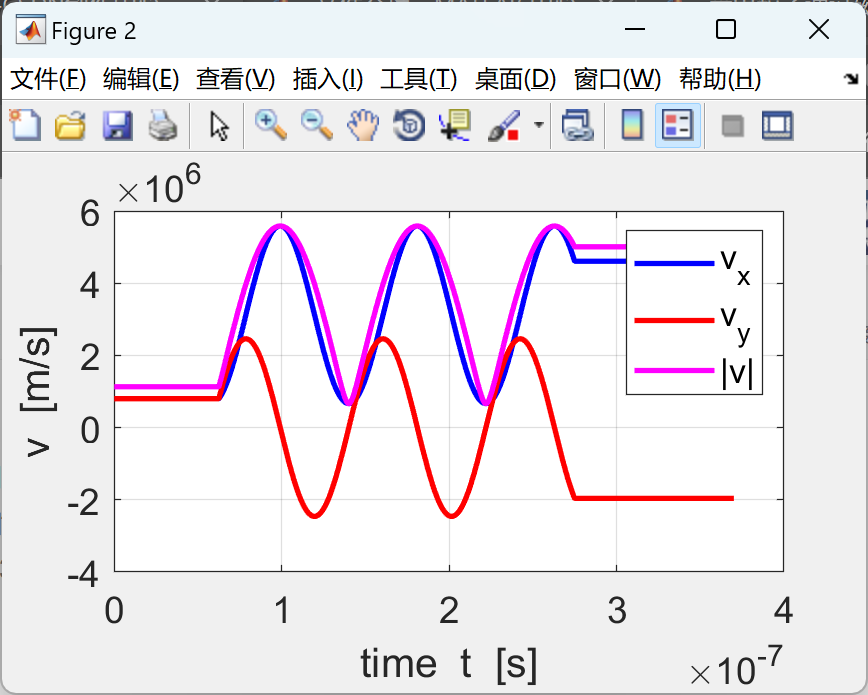
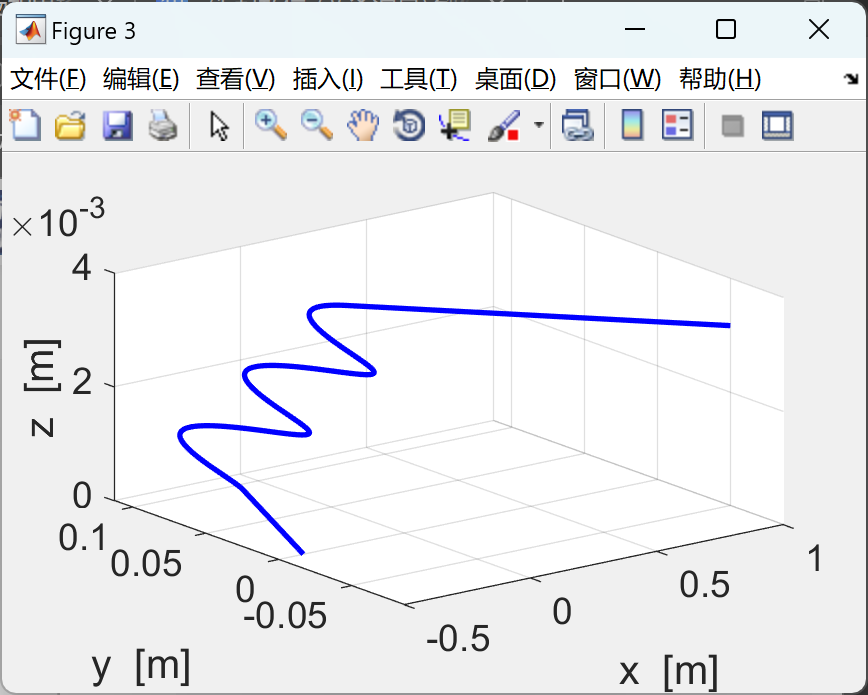
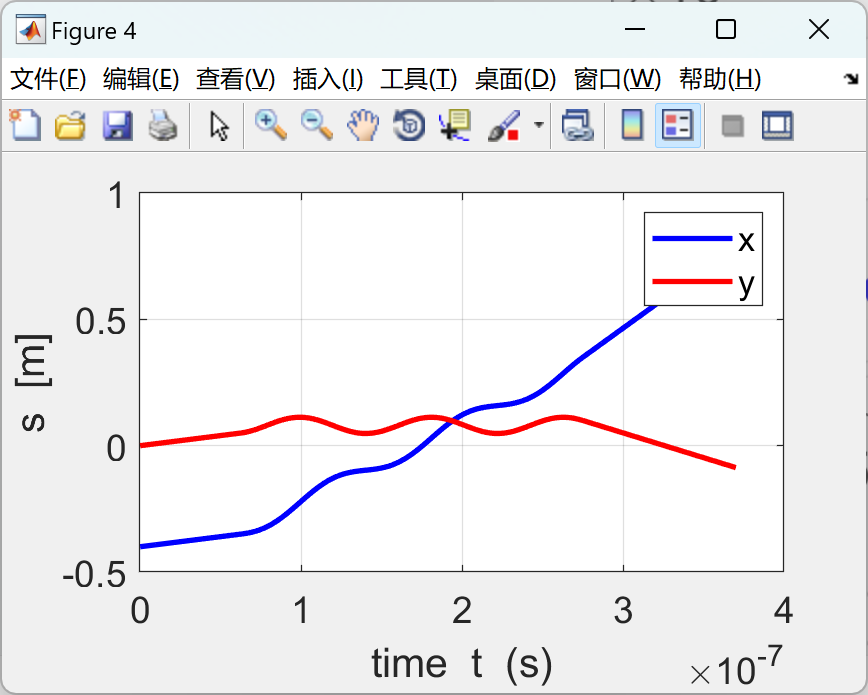
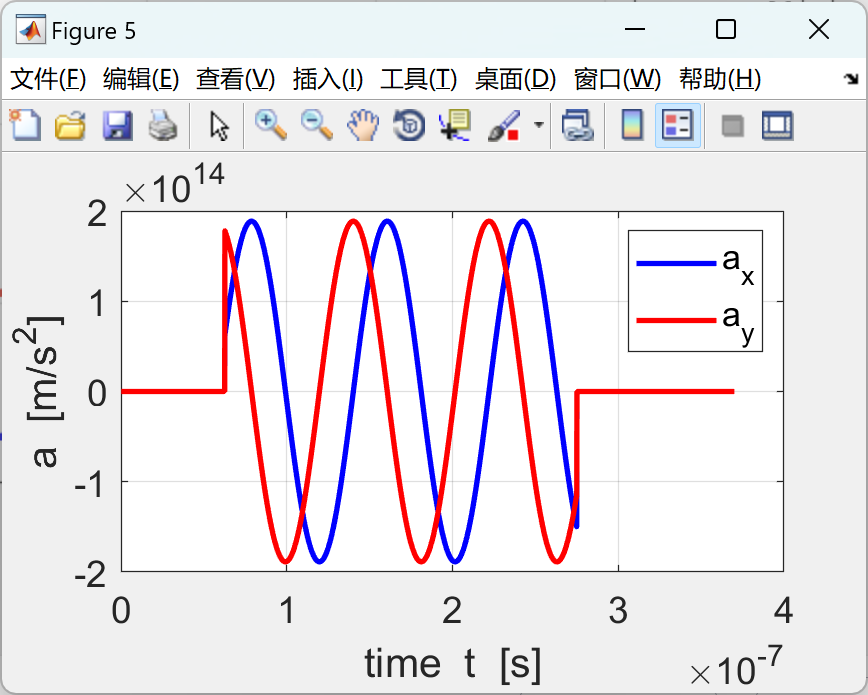
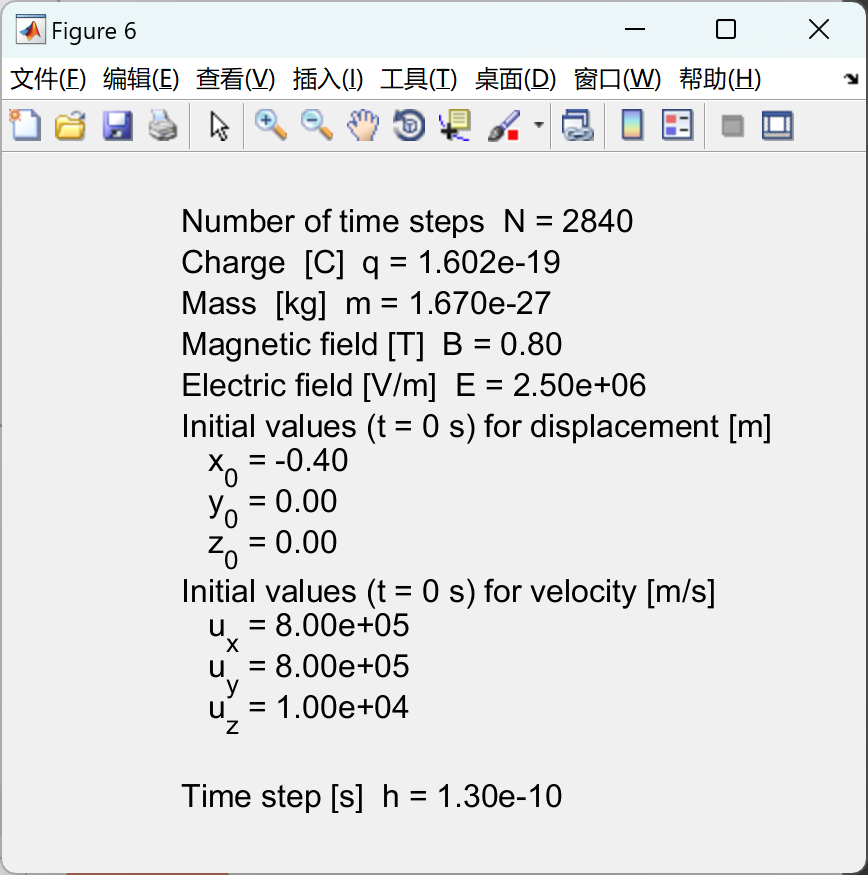
部分代码:
figure (5) % -------------------------------------------------------------
set(gcf,'units','normalized','position',[0.36,0.1,0.3,0.3]);
xP = t; yP = ax;
plot(xP,yP,'b','LineWidth',2)
hold on
xP = t; yP = ay;
plot(xP,yP,'r','LineWidth',2)
xlabel('time t [s]');
ylabel('a [m/s^2]');
legend('a_x','a_y');
grid on
set(gca,'fontsize',14);
figure (6) % -------------------------------------------------------------
set(gcf,'units','normalized','position',[0.67,0.1,0.3,0.4]);
xP = 0; yP = 0;
plot(xP,yP,'b','LineWidth',2)
axis([0 100 0 100]);
fs = 12;
px1 = 10; py1 = 98; dpx = 5; dpy = 7; px2 = 50;
% Number of elements N
tx1 = 'Number of time steps N = ';
tx2 = num2str(N,'%4.0f\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% charge q
py1 = py1 - dpy;
tx1 = 'Charge [C] q = ';
tx2 = num2str(q,'%2.3e\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% charge m
py1 = py1 - dpy;
tx1 = 'Mass [kg] m = ';
tx2 = num2str(m,'%2.3e\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% magnetic field B
py1 = py1 - dpy;
tx1 = 'Magnetic field [T] B = ';
tx2 = num2str(B,'%2.2f\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% electric field E
py1 = py1 - dpy;
tx1 = 'Electric field [V/m] E = ';
tx2 = num2str(E,'%2.2e\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
axis off
% initial positions x y z
py1 = py1 - 1*dpy;
tx1 = 'Initial values (t = 0 s) for displacement [m]';
tx2 = ' ';
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
py1 = py1 - 1*dpy;
tx1 = ' x_0 = ';
tx2 = num2str(x(1),'%2.2f\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
py1 = py1 - dpy;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
1. Griffiths, D. J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press.
- 书籍中的第11章介绍了带电粒子在电场和磁场中运动的基本理论和轨迹。
2. Reitz, J.R., Milford, F.J., & Christy, R.W. (2013). Foundations of Electromagnetic Theory (4th ed.). Addison-Wesley.
- 本书第9章探讨了带电粒子在电场和磁场中运动的数学描述和轨迹分析。
3. Purcell, E.M., & Morin, D.J. (2013). Electricity and Magnetism (3rd ed.). Cambridge University Press.
- 该教材的第5章涵盖了带电粒子在电场和磁场中的运动以及相关的轨迹描述。
🌈4 Matlab代码实现
相关文章:

【物理】带电粒子在磁场和电场中移动的 3D 轨迹研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【云原生】K8S二进制搭建上篇
目录 一、环境部署1.1操作系统初始化 二、部署etcd集群2.1 准备签发证书环境在 master01 节点上操作在 node01与02 节点上操作 三、部署docker引擎四、部署 Master 组件4.1在 master01 节点上操 五、部署Worker Node组件 一、环境部署 集群IP组件k8s集群master01192.168.243.1…...
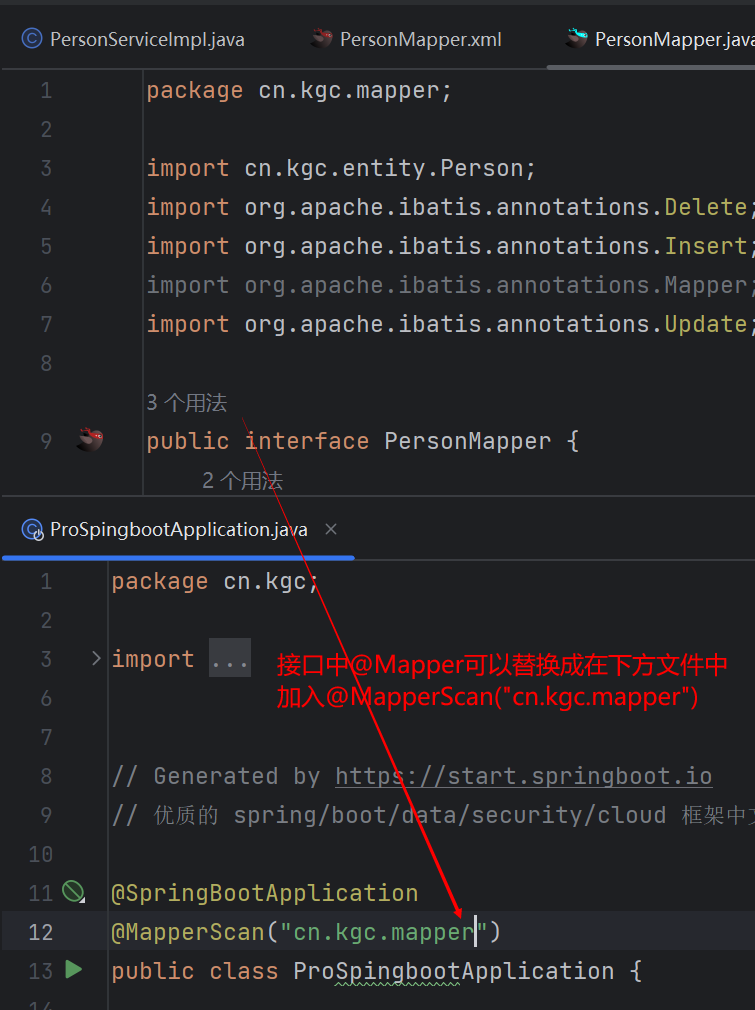
day49-Springboot
Springboot 1. Springboot简介 1.1 简介:Springboot来简化Spring应用开发的一个框架,约定大于配置 1.2 优点: 可以快速的构建独立运行的Spring项目; 框架内有Servlet容器,无需依赖外部,所以不需要达成w…...

Day 9 字符串
慢慢补。 Prefixes and Suffixes 水个代码先。 代码...

Promise用法
学习了promise之后,有点懂但让我说又说不出来,参考别人的记录一下。 1.什么是promise? 2.promise解决了什么问题 3.es6 promise语法 (1)then链式操作语法 (2)catch的语法 (3…...

JSP教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 JSP(全称Java Server Pages)是由Sun Microsystems公司主导创建的一种动态网页技术标准。JSP部署于网络服务器上,可以响应客户端发送的请求,并根据请求内容动态地生成HTML、XML或其他格式文档的Web网页,然后返…...
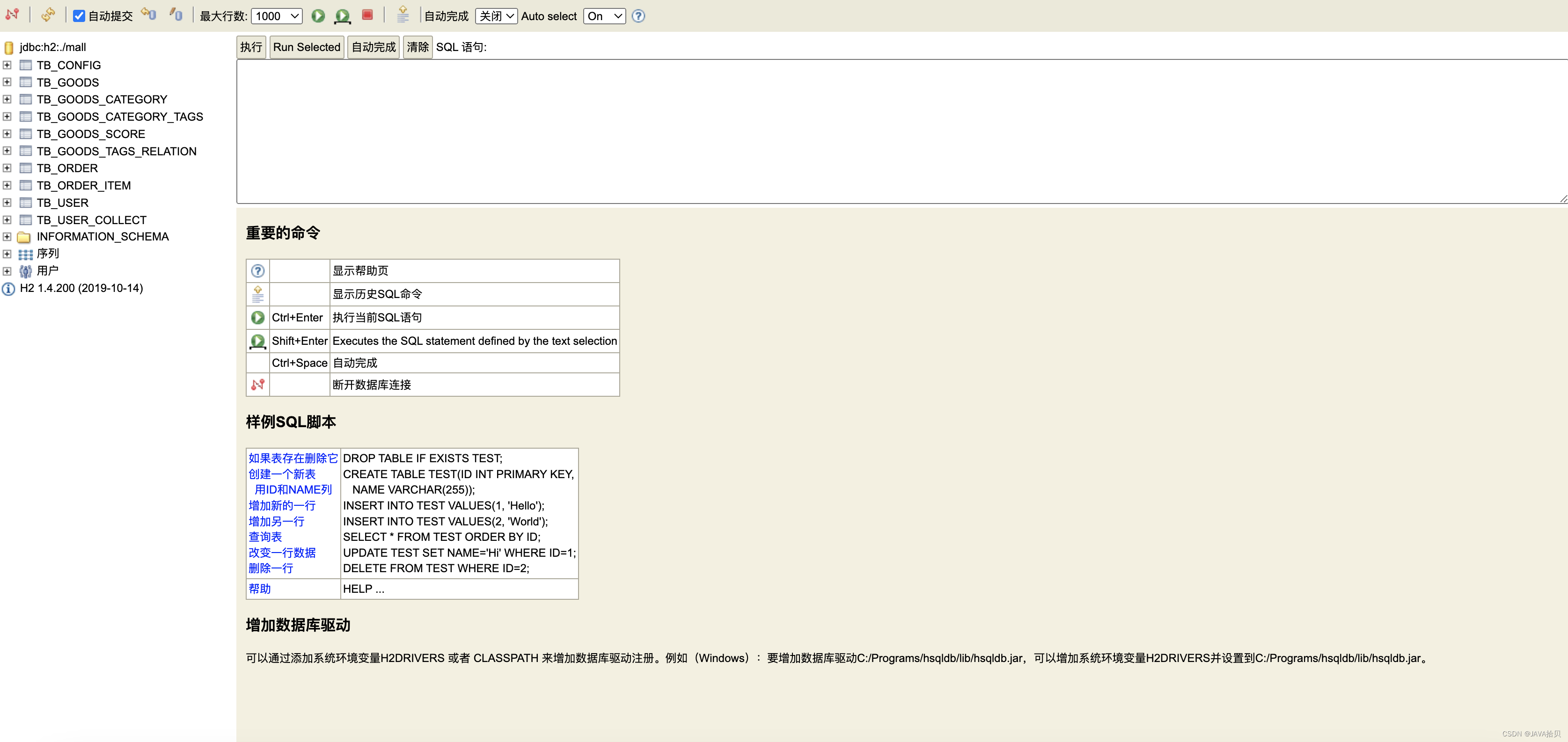
极简在线商城系统,支持docker一键部署
Hmart 给大家推荐一个简约自适应电子商城系统,针对虚拟商品在线发货,支持企业微信通知,支持docker一键部署,个人资质也可搭建。 前端 后端 H2 console 运行命令 docker run -d --name mall --restartalways -p 8080:8080 -e co…...
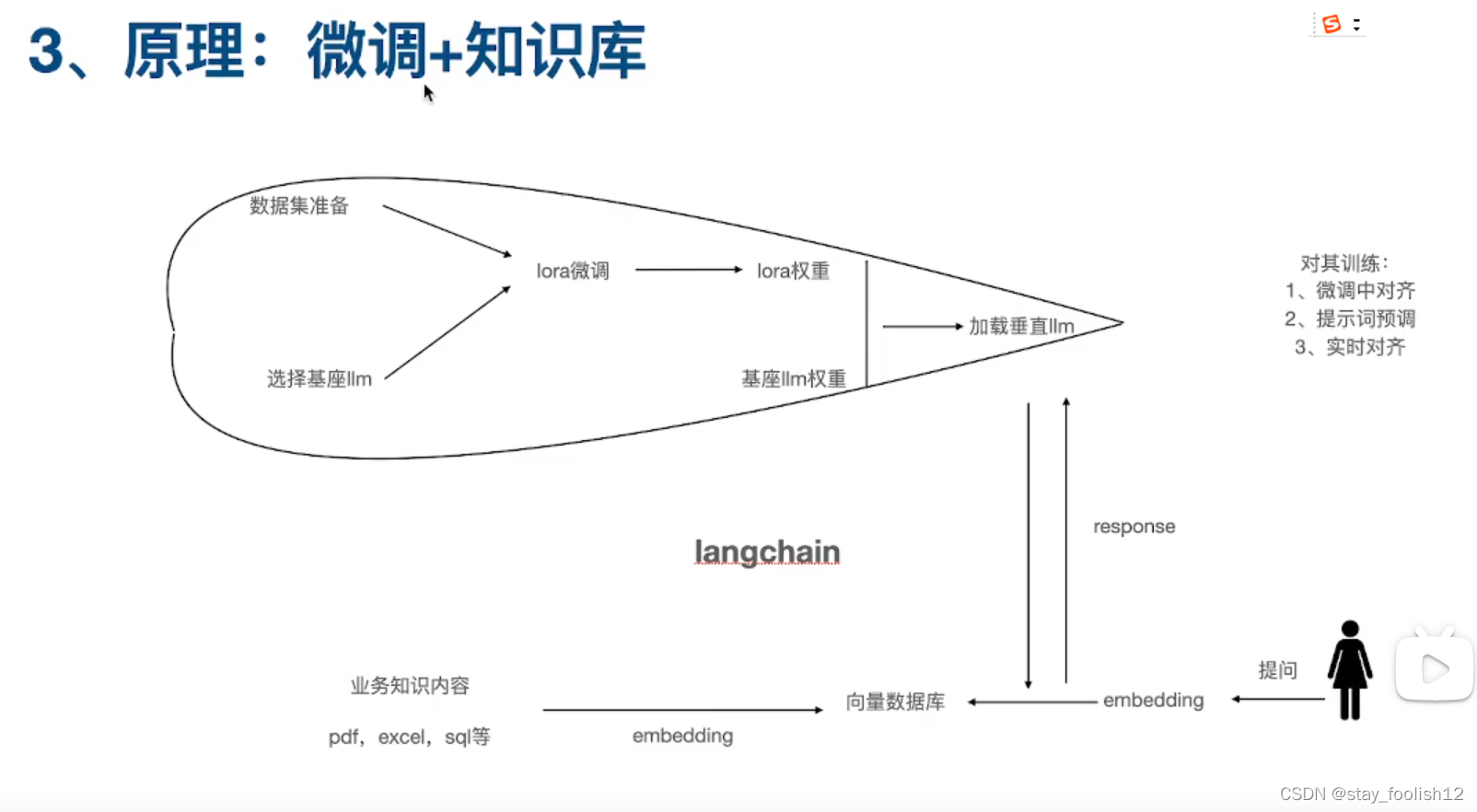
如何微调医疗大模型llm:llama2学习笔记
三个微调方向:简单医疗问答 临床问答 影像学 一般流程: 1 数据集准备 2 模型基座选择 3 微调 4 案例拆解 1 数据集准备:两种类型,一种文本一种影像 扩展,多模态 2 模型基座选择 多模态处理所有视频,文本…...
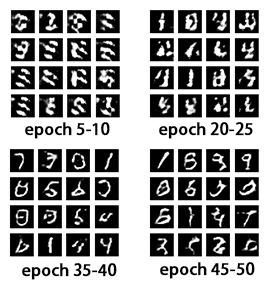
生成对抗网络DCGAN学习
在AI内容生成领域,有三种常见的AI模型技术:GAN、VAE、Diffusion。其中,Diffusion是较新的技术,相关资料较为稀缺。VAE通常更多用于压缩任务,而GAN由于其问世较早,相关的开源项目和科普文章也更加全面&#…...
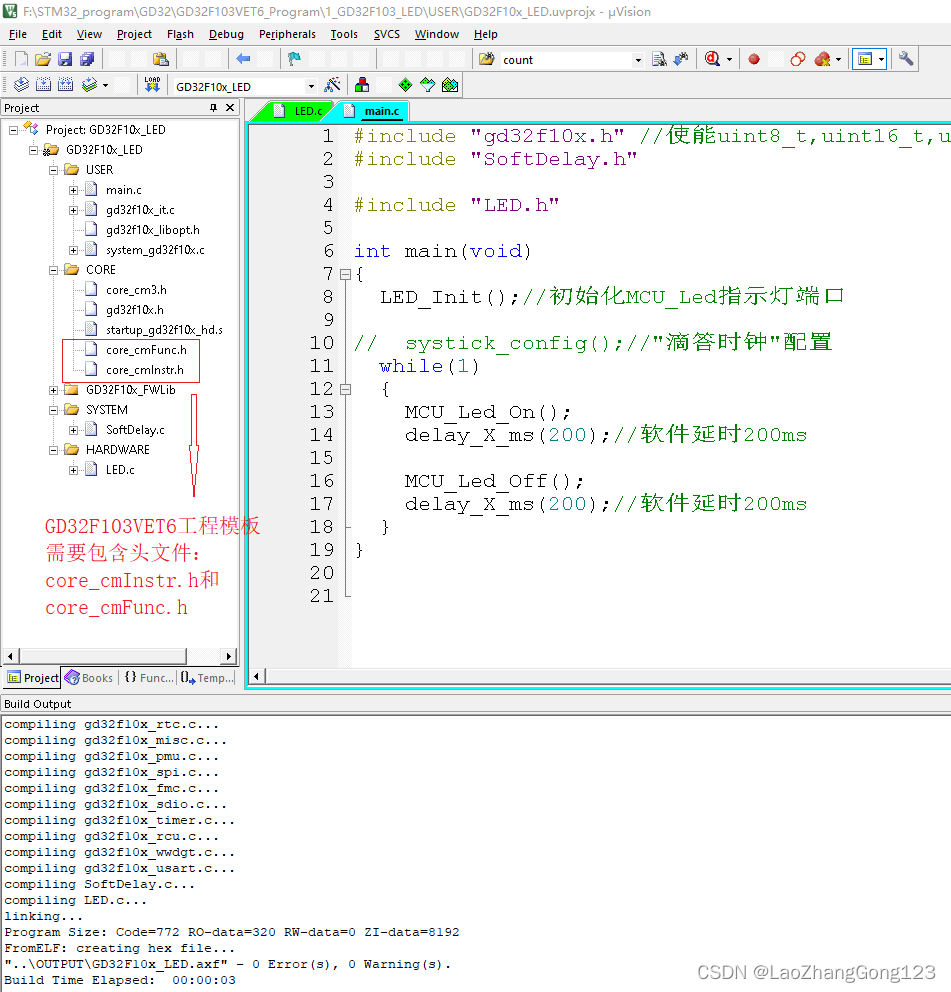
error: #5: cannot open source input file “core_cmInstr.h“
GD32F103VET6和STM32F103VET6引脚兼容。 GD32F103VET6工程模板需要包含头文件:core_cmInstr.h和core_cmFunc.h,这个和STM32F103还是有区别的,否则会报错,如下: error: #5: cannot open source input file "core…...

FastAPI 教程、结合vue实现前后端分离
英文版文档:https://fastapi.tiangolo.com/ 中文版文档:https://fastapi.tiangolo.com/zh/ 1、FastAPI 教程 简 介 FastAPI 和 Sanic 类似,都是 Python 中的异步 web 框架。相比 Sanic,FastAPI 更加的成熟、社区也更加的活跃。 …...
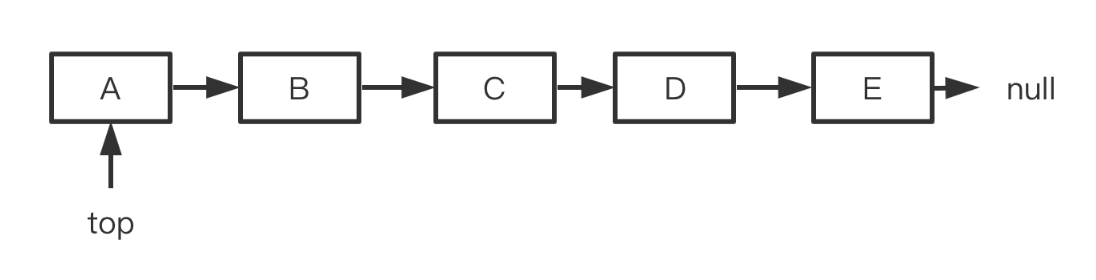
算法通关村第四关——如何基于数组(链表)实现栈
栈的基础知识 栈的特征 特征1 栈和队列是比较特殊的线性表,又被称为 访问受限的线性表。栈是很多表达式、符号等运算的基础,也是递归的底层实现(递归就是方法自己调用自己,在JVM的虚拟机栈中,一个线程中的栈帧就是…...

Postgresql警告日志的配置
文章目录 1.postgresql与日志有关的参数2.开启日志3.指定日志目录4.設置文件名format5.設置日志文件產出模式6.設置日志记录格式7.日誌輪換7.1非截斷式輪換7.2 截斷式輪換 8.日誌記錄內容8.1 log_statement8.2 log_min_duration_statement 9 輸出範本 1.postgresql与日志有关的…...

Java、JSAPI、 ssm架构 微信支付demo
1.前端 index.html <%page import"com.tenpay.configure.WxPayConfig"%> <% page language"java" contentType"text/html; charsetUTF-8" pageEncoding"UTF-8"%> <html><style>#fukuan{font-size: 50px;marg…...
MongoDB文档--基本安装-linux安装(mongodb环境搭建)-docker安装(挂载数据卷)-以及详细版本对比
阿丹: 前面了解了mongodb的一些基本概念。本节文章对安装mongodb进行讲解以及汇总。 官网教程如下: 安装 MongoDB - MongoDB-CN-Manual 版本特性 下面是各个版本的选择请在安装以及选择版本的时候参考一下: MongoDB 2.x 版本:…...

tomcat限制IP访问
tomcat可以通过增加配置,来对来源ip进行限制,即只允许某些ip访问或禁止某些来源ip访问。 配置路径:server.xml 文件下 标签下。与同级 <Valve className"org.apache.catalina.valves.RemoteAddrValve" allow"192.168.x.x&…...

互联网宠物医院系统开发:数字化时代下宠物医疗的革新之路
随着人们对宠物关爱意识的提高,宠物医疗服务的需求也日益增加。传统的宠物医院存在排队等待、预约难、信息不透明等问题,给宠物主人带来了诸多不便。而互联网宠物医院系统的开发,则可以带来许多便利和好处。下面将介绍互联网宠物医院系统开发…...

docker镜像批量导出导入
docker镜像批量导出导入 image_tar为存储镜像目录 删除所有容器 一、首先需要停止所有运行中的容器 docker stopdocker ps -a -q docker ps -a -q 意思是列出所有容器(包括未运行的),只显示容器编号,其中 -a : 显示所有的容器&…...
宇凡微2.4g遥控船开发方案,采用合封芯片
2.4GHz遥控船的开发方案是一个有趣且具有挑战性的项目。这样的遥控船可以通过无线2.4GHz频率进行远程控制,让用户在池塘或湖泊上畅游。以下是一个简要的2.4GHz遥控船开发方案: 基本构想如下 mcu驱动两个小电机,小电机上安装两个螺旋桨&#…...
RPC框架引入zookeeper服务注册与服务发现
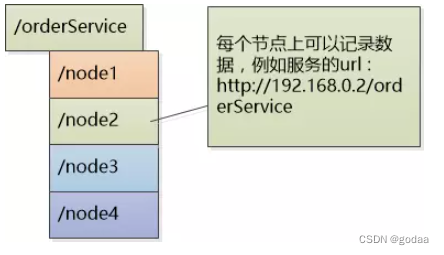
Zookeeper概念及其作用 ZooKeeper是一个分布式的,开放源码的分布式应用程序协调服务,是Google的Chubby一个开源的实现,是大数据生态中的重要组件。它是集群的管理者,监视着集群中各个节点的状态根据节点提交的反馈进行下一步合理…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

