【LeetCode每日一题】——1572.矩阵对角线元素的和
文章目录
- 一【题目类别】
- 二【题目难度】
- 三【题目编号】
- 四【题目描述】
- 五【题目示例】
- 六【题目提示】
- 七【解题思路】
- 八【时间频度】
- 九【代码实现】
- 十【提交结果】
一【题目类别】
- 矩阵
二【题目难度】
- 简单
三【题目编号】
- 1572.矩阵对角线元素的和
四【题目描述】
- 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
- 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
五【题目示例】
-
示例 1:
-
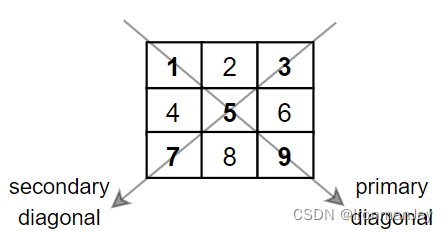
-
输入:mat = [[1,2,3],
[4,5,6],
[7,8,9]] -
输出:25
-
解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25。请注意,元素 mat[1][1] = 5 只会被计算一次。
-
-
示例 2:
- 输入:mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]] - 输出:8
- 输入:mat = [[1,1,1,1],
-
示例 3:
- 输入:mat = [[5]]
- 输出:5
六【题目提示】
- n = = m a t . l e n g t h = = m a t [ i ] . l e n g t h n == mat.length == mat[i].length n==mat.length==mat[i].length
- 1 < = n < = 100 1 <= n <= 100 1<=n<=100
- 1 < = m a t [ i ] [ j ] < = 100 1 <= mat[i][j] <= 100 1<=mat[i][j]<=100
七【解题思路】
- 定义i遍历二维数组的行数,j遍历二维数组的列数
- 如果i==j,说明是主对角线的元素
- 如果i+j==n-1,说明是副对角线的元素
- 采用
||进行判断,这样就不会将主对角线和副对角线的元素多加一次,因为只遍历了一次数组 - 然后将其求和,最后返回结果即可
八【时间频度】
- 时间复杂度: O ( n 2 ) O(n^2) O(n2), n n n为传入的正方形数组的长度
- 空间复杂度: O ( 1 ) O(1) O(1)
九【代码实现】
- Java语言版
class Solution {public int diagonalSum(int[][] mat) {int n = mat.length;int res = 0;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(i == j || i + j == n - 1){res += mat[i][j];}}}return res;}
}
- C语言版
int diagonalSum(int** mat, int matSize, int* matColSize)
{int n = matSize;int res = 0;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(i == j || i + j == n - 1){res += mat[i][j];}}}return res;
}
- Python语言版
class Solution:def diagonalSum(self, mat: List[List[int]]) -> int:n = len(mat)res = 0for i in range(0,n):for j in range(0,n):if i == j or i + j == n - 1:res += mat[i][j]return res
- C++语言版
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size();int res = 0;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(i == j || i + j == n - 1){res += mat[i][j];}}}return res;}
};
十【提交结果】
-
Java语言版
-
C语言版
-
Python语言版
-
C++语言版
相关文章:

【LeetCode每日一题】——1572.矩阵对角线元素的和
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 矩阵 二【题目难度】 简单 三【题目编号】 1572.矩阵对角线元素的和 四【题目描述】 给你一…...

牛客网Verilog刷题——VL55
牛客网Verilog刷题——VL55 题目答案 题目 请用Verilog实现4位约翰逊计数器(扭环形计数器),计数器的循环状态如下: 电路的接口如下图所示: 输入输出描述: 信号类型输入/输出位宽描述clkwireInput1系统…...
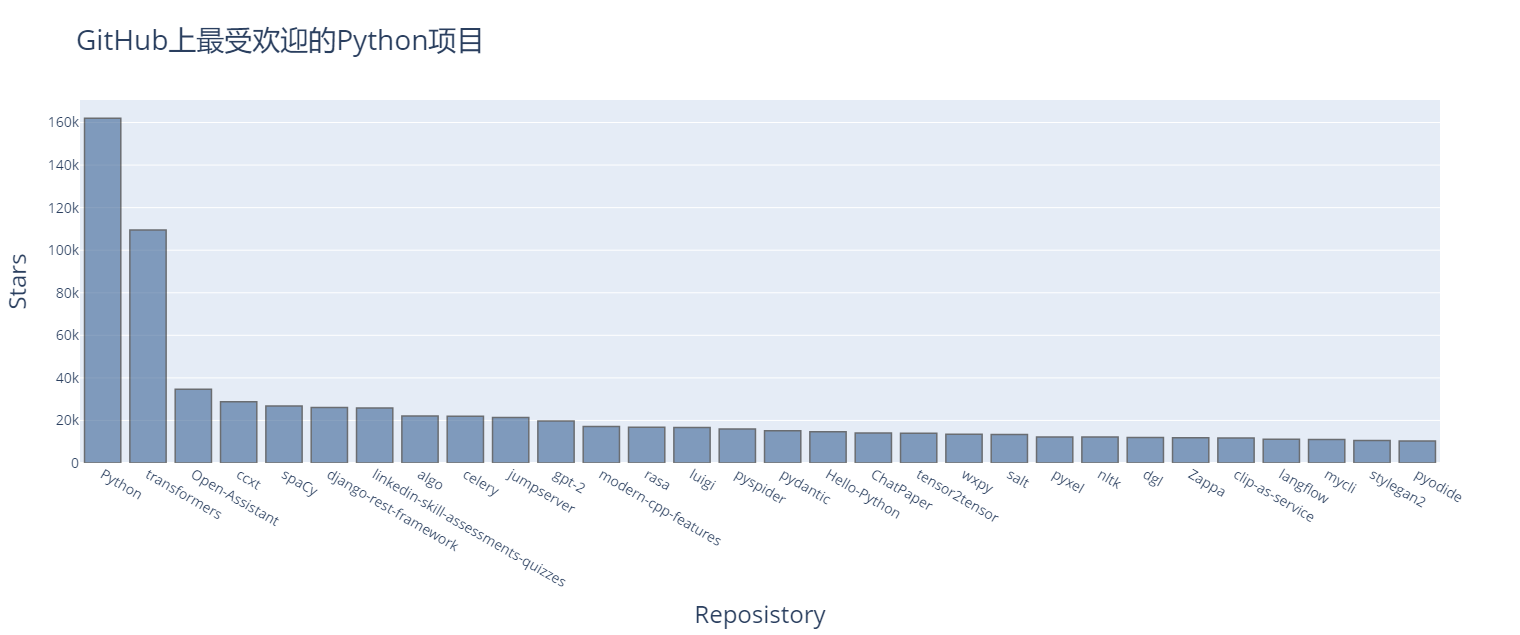
python中数据可视化
1.掷一个D6和一个D10 50000次的结果 die.py from random import randintclass Die:def __init__(self, num_sides6):self.num_sides num_sidesdef roll(self):return randint(1, self.num_sides) die_visual.py from die import Die from plotly.graph_objs import Bar, L…...

DASCTF 2023 0X401七月暑期挑战赛web复现
目录 <1> Web (1) EzFlask(python原型链污染&flask-pin) (2) MyPicDisk(xpath注入&文件名注入) (3) ez_cms(pearcmd文件包含) (4) ez_py(django框架 session处pickle反序列化) <1> Web (1) EzFlask(python原型链污染&flask-pin) 进入题目 得到源…...
go编译文件
1.编译go文件 go build [go文件]2.执行文件编译文件 ./demo [demo为go文件名称]...
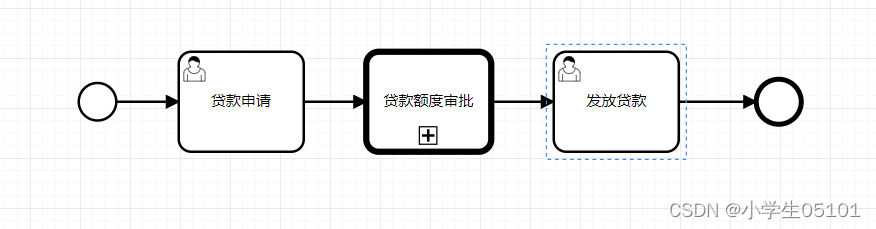
Flowable-子流程-调用活动
目录 定义图形标记XML内容界面操作使用示例子流程设计子流程的XML内容主流程设计主流程的XML内容 视频教程 定义 调用活动是在一个流程定义中调用另一个独立的流程定义,通常可以定义一些通用的流程作为 这种调用子流程,供其他多个流程定义复用。这种子流…...

java 并发
目录 什么是线程?什么是进程?为什么要有线程?有什么关系与区别?什么是守护线程?如何创建、启动 Java 线程?线程池参数详细解释Callable接口和Future类偏向锁 / 轻量级锁 / 重量级锁synchronized 和 java.ut…...
【MySQL】DDL和DML
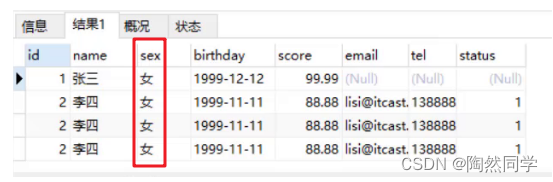
4,DDL:操作数据库 我们先来学习DDL来操作数据库。而操作数据库主要就是对数据库的增删查操作。 4.1 查询 查询所有的数据库 SHOW DATABASES; 运行上面语句效果如下: 上述查询到的是的这些数据库是mysql安装好自带的数据库,我们以后不要操…...

使用python框架FastAPI
中文文档 Python ORM之SQLAlchemy Fastapi大型项目目录规划 SQL数据库操作 依赖项Depends 待看 和APIRouter from sqlalchemy import create_engine from sqlalchemy.ext.declarative import declarative_base from sqlalchemy.orm import sessionmakerapp FastAPI()SQ…...
Vue实现leafletMap自定义绘制线段 并且删除指定的已绘制的点位
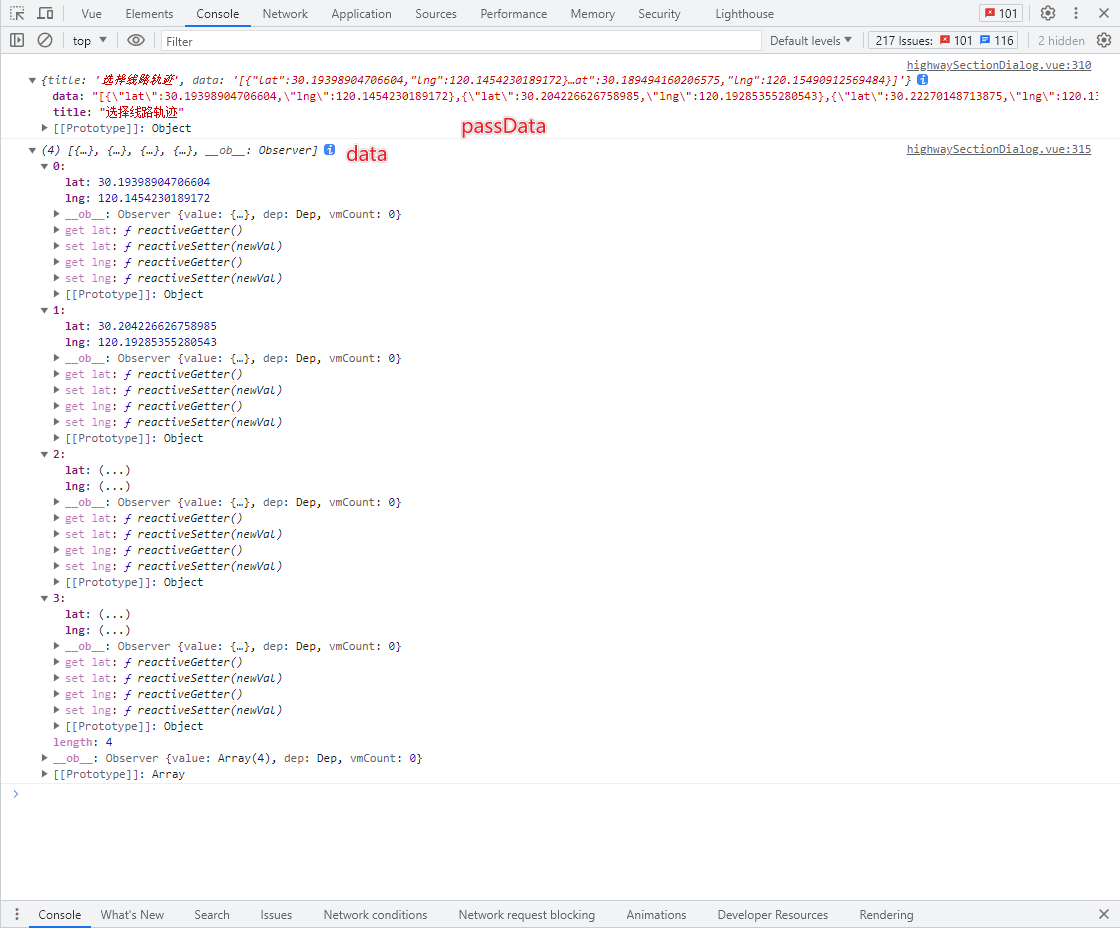
效果:点击表格可实现选中地图点位,删除按钮点击可删除对应点位并且重新绘制线段,点击确定按钮 保存已经绘制的点位信息传给父组件 并且该组件已实现回显 完整的组件代码如下 文件名称为: leafletMakePointYt <!--* Descripti…...

ChatGPT辅助写论文:提升效率与创造力的利器
写作是人类最重要的交流方式之一,也是学术研究中不可或缺的环节。然而,写作并不是一件容易的事情,尤其是对于科研人员来说,他们需要花费大量的时间和精力来撰写高质量的论文,并且面临着各种各样的挑战,如语…...
)
面试攻略,Java 基础面试 100 问(六)
JAVA 泛型 泛型提供了编译时类型安全检测机制,该机制允许程序员在编译时检测到非法的类型。泛型的本 质是参数化类型,也就是说所操作的数据类型被指定为一个参数。比如我们要写一个排序方法, 能够对整型数组、字符串数组甚至其他任何类型的…...
图解系列 DNS查找过程和DNS缓存
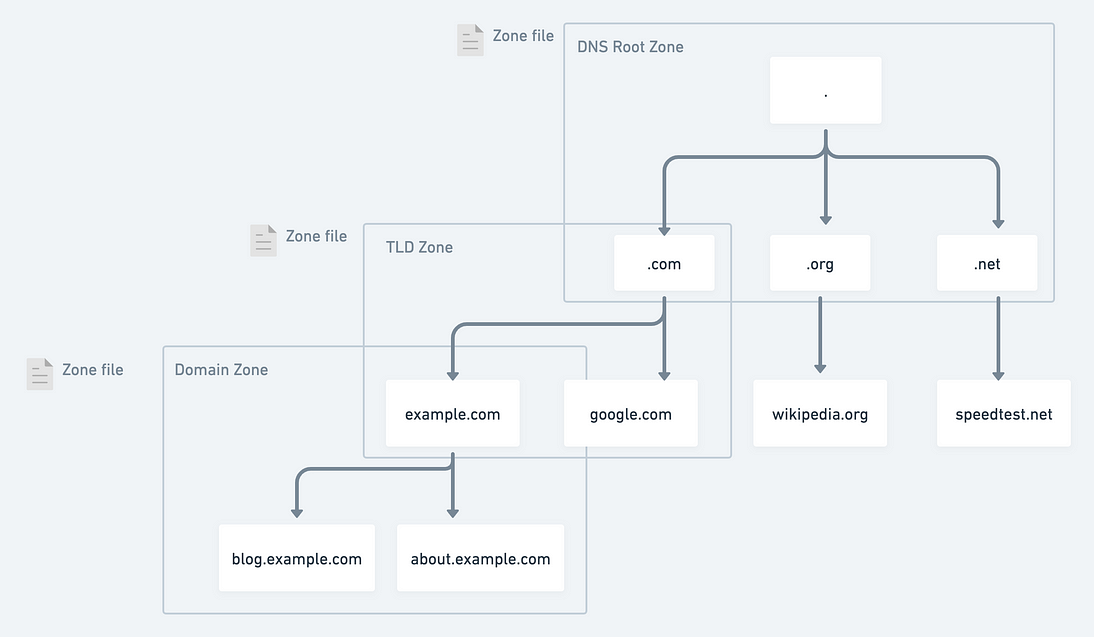
DNS 充当地址簿。它将人类可读的域名 (google.com) 转换为机器可读的 IP 地址 (142.251.46.238)。 开局一张图 来自:https://xiaolishen.medium.com/the-dns-lookup-journey-240e9a5d345c 寻址流程 查询浏览器缓存:当你输入一个域名后,浏览…...
《吐血整理》高级系列教程-吃透Fiddler抓包教程(21)-如何使用Fiddler生成Jmeter脚本-上篇
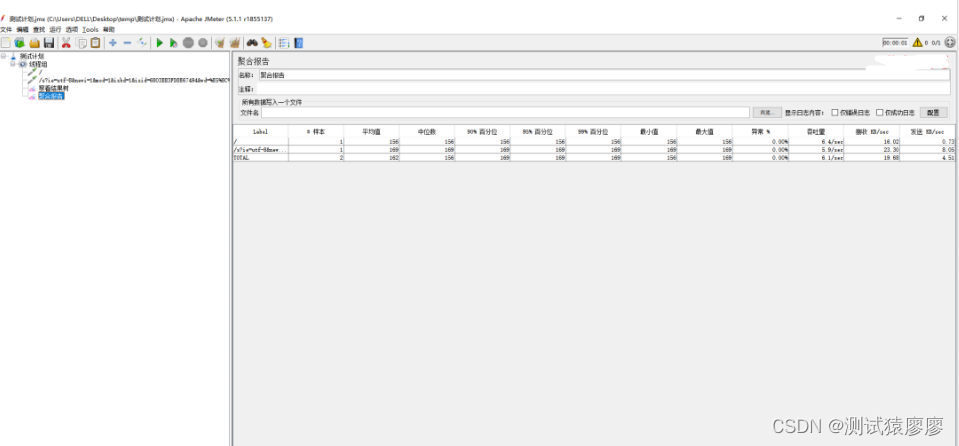
1.简介 我们知道Jmeter本身可以录制脚本,也可以通过BadBoy,BlazeMeter等工具进行录制,其实Fiddler也可以录制Jmter脚本(而且有些页面,由于安全设置等原因,使用Jmeter直接无法打开录制时,这时就…...

vim中出现复制不对齐-乱码问题
不对齐解决: 使用纯文本模式粘贴:在进入 Vim 编辑器后,先按下 :set paste 进入插入模式,然后再进行粘贴操作。这样可以确保粘贴的文本以纯文本格式插入,而不会触发自动缩进或其他格式化操作 中文乱码问题:…...

华为OD机考真题--单词接龙--带答案
2023华为OD统一考试(AB卷)题库清单-带答案(持续更新)or2023年华为OD真题机考题库大全-带答案(持续更新) 题目描述: 单词接龙的规则是: 用于接龙的单词首字母必须要前一个单词的尾字母…...
排序进行曲-v3.0
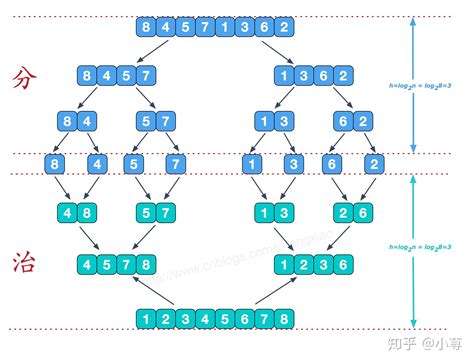
文章目录 小程一言归并排序步骤举例总结时间复杂度分析:空间复杂度分析:注意 应用场景总结 实际举例Other 代码实现结果解释 小程一言 这篇文章是在排序进行曲2.0之后的续讲, 这篇文章主要是对归并排序进行细致分析,以及操作。 希…...
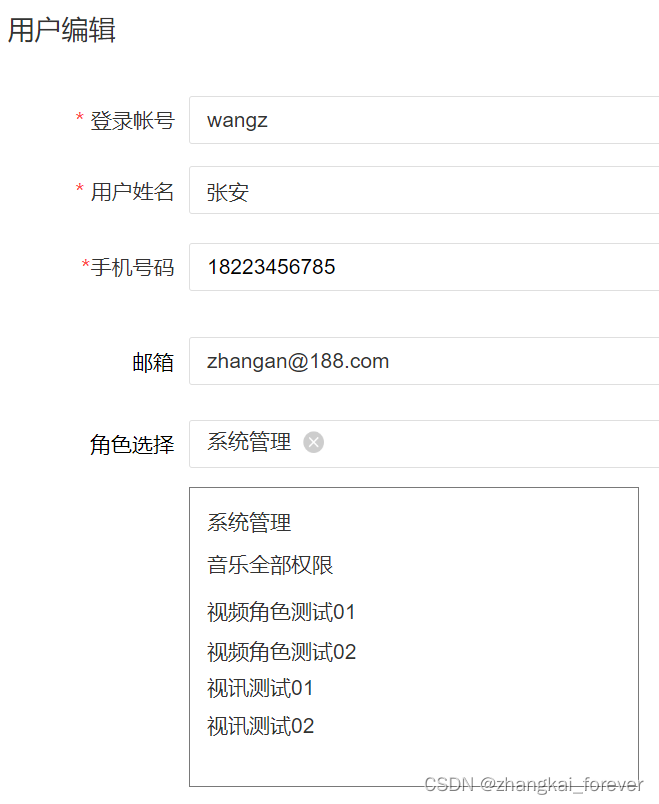
编辑列表操作时的一些思考,关于全量和增量操作
假设我有一个这样的页面,需要对用户的信息做编辑操作 角色下面有一些菜单项,通过一张角色-菜单关系表来维护,那么我要在编辑用户后也要对用户角色关系表做修改,是经过两次比较分别计算出需要增加或者删除的角色用户关系࿰…...
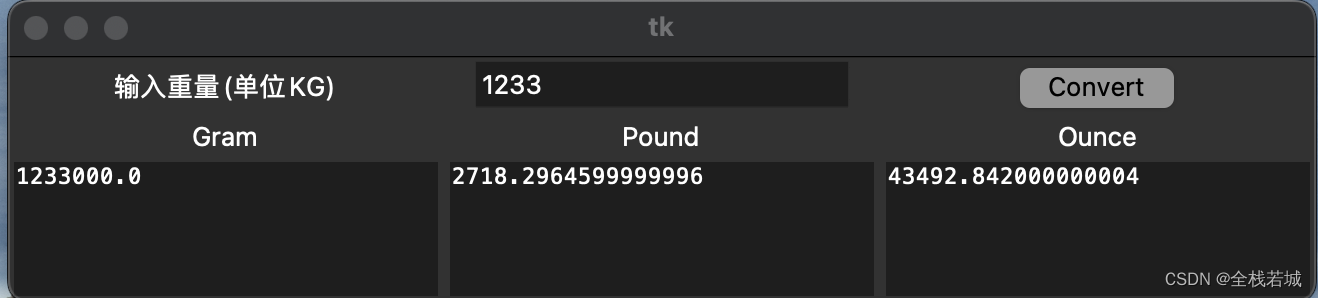
【python】Python tkinter库实现重量单位转换器的GUI程序
文章目录 前言学到什么?导入模块和库创建一个GUI窗口定义函数 from_kg()创建标签、输入框、文本框和按钮设置组件的布局运行窗口循环完整代码运行效果结束语 前言 这段代码是一个简单的重量单位转换器的 GUI 程序,使用了 Python 的 tkinter 库来创建图形界面。该程…...

CVPR2023新作:源数据集对迁移学习性能的影响以及相应的解决方案
Title: A Data-Based Perspective on Transfer Learning (迁移学习的基于数据的观点) Affiliation: MIT (麻省理工学院) Authors: Saachi Jain, Hadi Salman, Alaa Khaddaj, Eric Wong, Sung Min Park, Aleksander Mądry Keywords: transfer learning, source dataset, dow…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
