排序进行曲-v3.0
小程一言
这篇文章是在排序进行曲2.0之后的续讲,
这篇文章主要是对归并排序进行细致分析,以及操作。
希望大家多多支持
图片: 
归并排序
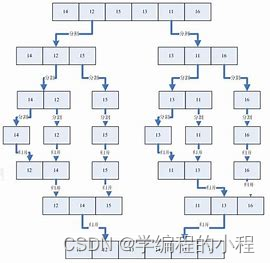
归并排序是一种分治算法,它将一个待排序的数组分成两个子数组,分别对这两个子数组进行排序,然后再将
两个有序的子数组合并为一个有序的数组。这个过程不断地递归进行,直到最后将整个数组排序完成。
步骤
分割(Divide):将待排序的数组不断地二分,直到分成单个元素的子数组。这个过程可以通过递归实现。递归的终止条件是数组的长度为1。合并(Merge):将相邻的两个有序子数组合并为一个有序的子数组。合并的方法是比较两个子数组的第一个元素,将较小的元素放在新的子数组中,并将该元素从原子数组中移除。然后继续比较两个子数组的新的第一个元素,重复这个过程,直到其中一个子数组为空。将剩余的另一个子数组直接拼接到新的子数组的末尾。递归合并(Recursive Merge):对每个单个元素的子数组进行排序和合并。当子数组长度为1时,它已经是有序的,直接返回该子数组即可。对于长度大于1的子数组,先将其分割成两个子数组,然后分别对这两个子数组进行递归合并,得到两个有序的子数组。最后将这两个有序的子数组进行合并,得到一个更大的有序子数组。
举例
假设我们要对数组 [5, 3, 8, 2, 9, 1] 进行排序。分割(Divide):首先将数组分成两个子数组,即 [5, 3, 8] 和 [2, 9, 1]。递归合并(Recursive Merge):对两个子数组分别进行递归合并排序。首先对 [5, 3, 8] 进行递归合并排序,得到有序子数组 [3, 5, 8]。然后对 [2, 9, 1] 进行递归合并排序,得到有序子数组 [1, 2, 9]。合并(Merge):将两个有序子数组 [3, 5, 8] 和 [1, 2, 9] 进行合并。比较两个子数组的第一个元素,将较小的元素放入新的子数组中,并将该元素从原子数组中移除。依次比较,得到新的子数组[1, 2, 3, 5, 8, 9]。最终,整个数组 [5, 3, 8, 2, 9, 1] 经过归并排序后,得到有序数组 [1, 2, 3, 5, 8, 9]。
总结
这个例子展示了归并排序的过程,通过不断地分割和合并子数组,最终将整个数组排序。在每一次合并过程中,我们都是将两个有序的子数组合并为一个有序的子数组,这保证了最终得到的整个数组是有序的。

)### 复杂度分析
归并排序的时间复杂度为 O(nlogn),空间复杂度为 O(n)。
时间复杂度分析:
分割(Divide):每次将数组分割成两个子数组,分割的时间复杂度为 O(logn)。因为每次分割都将数组的大小减半,所以需要进行 logn 次分割。
合并(Merge):对于每一次合并操作,需要比较两个子数组的元素并将较小的元素放入新的子数组中,合并的时间复杂度为 O(n)。因为每次合并都是将两个子数组的元素全部比较一遍,所以需要进行 n 次合并。
递归合并(Recursive Merge):对于长度为 n 的数组,需要进行 logn 次递归合并,每次递归合并的时间复杂度为 O(n)。所以总的时间复杂度为 O(nlogn)。
空间复杂度分析:
在每次递归合并的过程中,需要创建临时数组来存储合并后的子数组,临时数组的空间复杂度为 O(n)。
在每次递归合并完成后,临时数组会被销毁,所以整个归并排序的空间复杂度为 O(n)。
注意
归并排序是一种稳定的排序算法,因为在合并的过程中,如果两个元素相等,我们会先将左边的元素放入新的子数组中,这样可以保持原始数组中相等元素的相对顺序不变。
应用场景
排序问题:归并排序可以用于对数组、链表等数据结构进行排序。它的时间复杂度为O(nlogn),在处理大规模数据集时表现较好。大规模数据的排序:归并排序适用于需要对大规模数据进行排序的场景。由于归并排序是一种分治算法,可以将大规模数据分割成较小的子问题进行排序,然后再将排序好的子问题合并起来。外部排序:归并排序是一种适用于外部排序的算法。外部排序是指需要处理的数据量大于计算机内存容量,需要将数据存储在外部存储介质(如硬盘)中进行排序。归并排序的特点是每次只需要读取一部分数据到内存中进行排序,然后将排序好的数据写回外部存储介质。并行计算:归并排序可以通过并行计算的方式提高排序的效率。由于归并排序的分治特性,可以将大规模数据分割成多个子问题进行排序,然后再将排序好的子问题合并起来。这种并行计算的方式可以利用多核处理器或分布式计算环境来加速排序过程。
总结
归并排序适用于排序问题,特别是大规模数据的排序和外部排序场景。它具有稳定的时间复杂度和较好的并行性能,因此在实际应用中被广泛使用。
实际举例
数组排序:归并排序可以用于对数组进行排序。例如,给定一个整数数组,可以使用归并排序将数组中的元素按照升序进行排序。链表排序:归并排序也可以用于对链表进行排序。例如,给定一个链表,可以使用归并排序将链表中的节点按照升序进行排序。文件排序:归并排序可以用于对大规模文件进行排序。例如,当需要对一个非常大的文件进行排序时,可以使用归并排序算法将文件分割成多个较小的部分,分别对这些部分进行排序,然后再将排序好的部分合并起来。数据库排序:归并排序可以用于对数据库中的数据进行排序。例如,在某个数据库表中有大量的数据需要按照某个字段进行排序,可以使用归并排序算法将数据分割成多个较小的部分,分别对这些部分进行排序,然后再将排序好的部分合并起来。外部排序:归并排序是一种适用于外部排序的算法。外部排序是指需要处理的数据量大于计算机内存容量,需要将数据存储在外部存储介质(如硬盘)中进行排序。归并排序的特点是每次只需要读取一部分数据到内存中进行排序,然后将排序好的数据写回外部存储介质。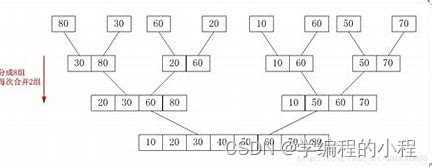
Other
这些例子只是归并排序在实际中的一些应用,实际上归并排序的思想和方法也可以应用于其他问题,只需要将问题分割成更小的子问题,并将子问题的结果合并起来。
代码实现
public class MergeSort {public static void mergeSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}int[] temp = new int[arr.length];mergeSort(arr, 0, arr.length - 1, temp);}private static void mergeSort(int[] arr, int start, int end, int[] temp) {if (start >= end) {return;}int mid = start + (end - start) / 2;mergeSort(arr, start, mid, temp);mergeSort(arr, mid + 1, end, temp);merge(arr, start, mid, end, temp);}private static void merge(int[] arr, int start, int mid, int end, int[] temp) {int left = start;int right = mid + 1;int index = start;while (left <= mid && right <= end) {if (arr[left] <= arr[right]) {temp[index++] = arr[left++];} else {temp[index++] = arr[right++];}}while (left <= mid) {temp[index++] = arr[left++];}while (right <= end) {temp[index++] = arr[right++];}for (int i = start; i <= end; i++) {arr[i] = temp[i];}}public static void main(String[] args) {int[] arr = {5, 2, 8, 4, 9, 1, 3, 7, 6};mergeSort(arr);System.out.println("Sorted array: " + Arrays.toString(arr));}
}

结果
运行以上代码,输出结果为:Sorted array: [1, 2, 3, 4, 5, 6, 7, 8, 9],表示归并排序对给定的数组进行了升序排序。
解释
在mergeSort方法中,首先判断数组的长度是否小于等于1,如果是,则直接返回。然后创建一个临时数组temp,并调用mergeSort方法对数组进行递归排序。在mergeSort方法中,首先计算出数组的中间位置mid,然后分别对左半部分和右半部分进行递归排序,最后调用merge方法将排序好的左右两部分合并起来。在merge方法中,使用双指针分别指向左半部分和右半部分的起始位置,比较两个指针所指的元素大小,将较小的元素放入临时数组temp中,并将对应指针向后移动一位。最后将临时数组temp中的元素复制回原数组arr中,完成排序。
图片: 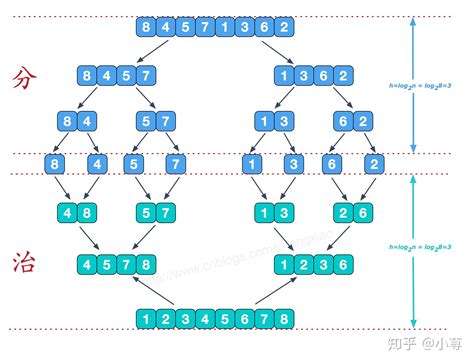
相关文章:

排序进行曲-v3.0
文章目录 小程一言归并排序步骤举例总结时间复杂度分析:空间复杂度分析:注意 应用场景总结 实际举例Other 代码实现结果解释 小程一言 这篇文章是在排序进行曲2.0之后的续讲, 这篇文章主要是对归并排序进行细致分析,以及操作。 希…...
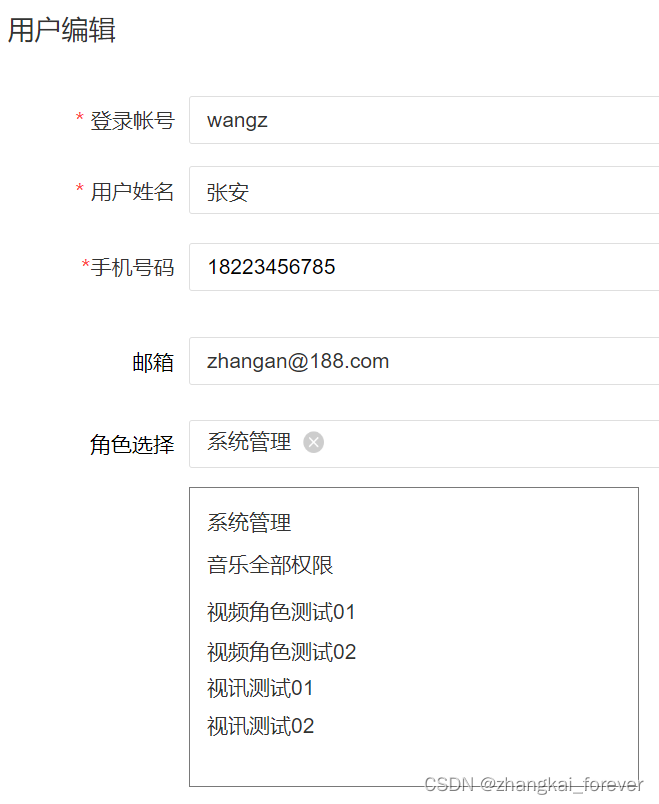
编辑列表操作时的一些思考,关于全量和增量操作
假设我有一个这样的页面,需要对用户的信息做编辑操作 角色下面有一些菜单项,通过一张角色-菜单关系表来维护,那么我要在编辑用户后也要对用户角色关系表做修改,是经过两次比较分别计算出需要增加或者删除的角色用户关系࿰…...
【python】Python tkinter库实现重量单位转换器的GUI程序
文章目录 前言学到什么?导入模块和库创建一个GUI窗口定义函数 from_kg()创建标签、输入框、文本框和按钮设置组件的布局运行窗口循环完整代码运行效果结束语 前言 这段代码是一个简单的重量单位转换器的 GUI 程序,使用了 Python 的 tkinter 库来创建图形界面。该程…...

CVPR2023新作:源数据集对迁移学习性能的影响以及相应的解决方案
Title: A Data-Based Perspective on Transfer Learning (迁移学习的基于数据的观点) Affiliation: MIT (麻省理工学院) Authors: Saachi Jain, Hadi Salman, Alaa Khaddaj, Eric Wong, Sung Min Park, Aleksander Mądry Keywords: transfer learning, source dataset, dow…...
《TCP IP 网络编程》第十五章
第 15 章 套接字和标准I/O 15.1 标准 I/O 的优点 标准 I/O 函数的两个优点: 除了使用 read 和 write 函数收发数据外,还能使用标准 I/O 函数收发数据。下面是标准 I/O 函数的两个优点: 标准 I/O 函数具有良好的移植性标准 I/O 函数可以利用…...

新特性解读 | MySQL 8.0 字段信息统计机制
作者通过一个案例详细说明了 MySQL 8.0 字段信息统计机制的相关参数和使用方式。 作者:杨奇龙 网名“北在南方”,资深 DBA,主要负责数据库架构设计和运维平台开发工作,擅长数据库性能调优、故障诊断。 本文来源:原创投…...

基于Java+Swing实现超级玛丽游戏
基于JavaSwing实现超级玛丽游戏 一、系统介绍二、功能展示三、其他系统 一、系统介绍 超级玛丽小游戏的JAVA程序,进入游戏后首先按空格键开始,利用方向键来控制的马里奥的移动,同时检测马里奥与场景中的障碍物和敌人的碰撞,并判断…...

Day12-1-Webpack前端工程化开发
Webpack前端工程化 1 案例-webpack打包js文件 1 在index.html中编写代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><me…...

JUnit教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 JUnit是一个Java语言的单元测试框架。它由Kent Beck和Erich Gamma建立,逐渐成为源于Kent Beck的sUnit的xUnit家族中最为成功的一个。 JUnit有它自己的JUnit扩展生态圈。多数Java的开发环境都已经集成了JUnit作为单元测试的工具。JUnit是由 Erich Gamma 和…...

Hive 安装介绍
介绍 Hive是基于Hadoop的一个数据仓库工具,可以将结构化的数据文件映射为一张数据库表,并提供类SQL查询功能。 其本质是将SQL转换为MapReduce的任务进行运算,底层由HDFS来提供数据的存储,说白了hive可以理解为一个将SQL转换为Ma…...

npm ERR! code EPERM npm ERR! syscall unlink npm ERR!错误解决方法
npm ERR! code EPERM npm ERR! syscall unlink npm ERR!错误解决方法 1、问题描述2、解决方法 1、问题描述 由于之前电脑系统的原因,电脑重置了一下,之前安装的环境都没了,然后在重新安装node.js后在使用npm安装时总是报如下错误:…...
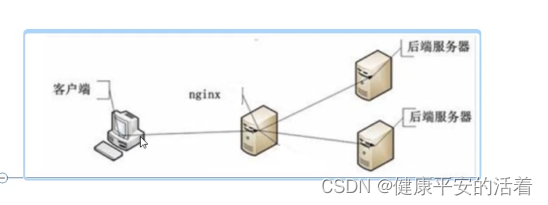
redis 高级篇4 分布式锁
一 redis架构图 1.1 redis的架构图 1.2 分布式锁满足条件 1.独占性;2.高可用;3.防死锁;4.不乱抢;5.重入性 二 分布式锁的案例情况 2.1 分布式锁1:单机分布式部署 描述: 使用lock锁和synchronized,单机…...

TPU-NNTC 编译部署LPRNet 车牌识别算法
TPU-NNTC 编译部署LPRNet 车牌识别算法 注意: 由于SOPHGO SE5微服务器的CPU是基于ARM架构,以下步骤将在基于x86架构CPU的开发环境中完成 初始化开发环境(基于x86架构CPU的开发环境中完成)模型转换 (基于x86架构CPU的开发环境中完成) 处理后的LPRNet 项…...
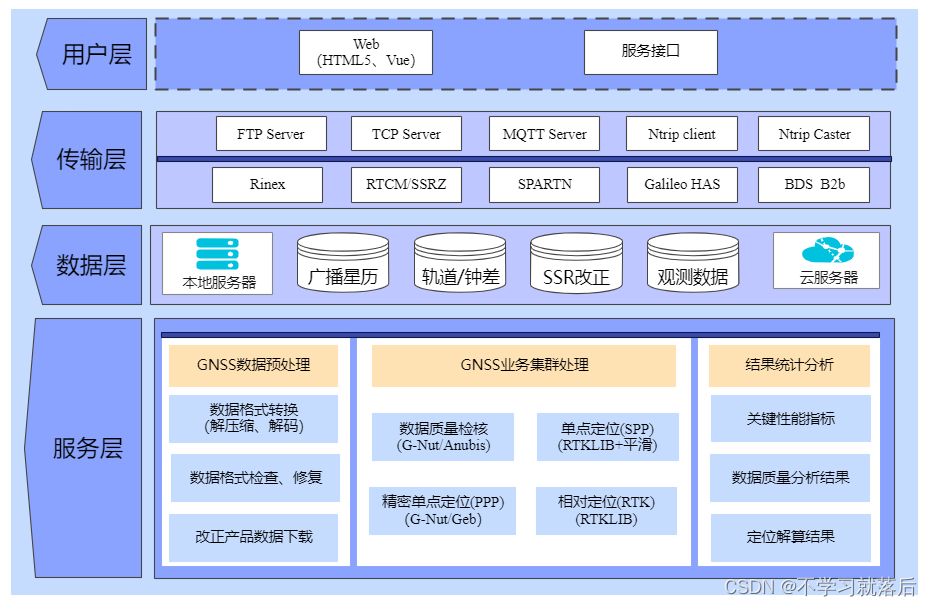
在线/开源GNSS处理软件/平台介绍
当前,存在较多的GNSS开源/免费软件,可用于质量检核、RTK解算和PPP解算等,本文总结了部分常用的处理软件,其详细信息如表1和表2所示。 表1 常用GNSS预处理(格式转换、质量检核)软件: 软件名称 …...

SpringBoot集成企业微信群聊机器人消息
目录 参考文档概述一、功能作用二、应用场景三、 群机器人发送限制四、创建机器人1、添加2、群机器人Webhook地址 五、发送消息1、文本 text请求体 图文连接 news 参考文档 官方文档 企业微信群机器人应用 概述 现在很多企业都在使用企业微信进行工作交流,自从企…...

五、驱动 - 音频系统硬件电路
文章目录 1. 音频系统硬件电路结构2. 蓝牙音频2.1 音乐播放2.2 VoIP通话2.3 4G通话3. 其他3.1 什么是S/PDIF1. 音频系统硬件电路结构 录音放音设备:mic、speaker、耳机、听筒这些带有录音放音功能的设备(因为录放设备可能是模拟设备也可能是数字设备,所以接口可能是模拟接口…...
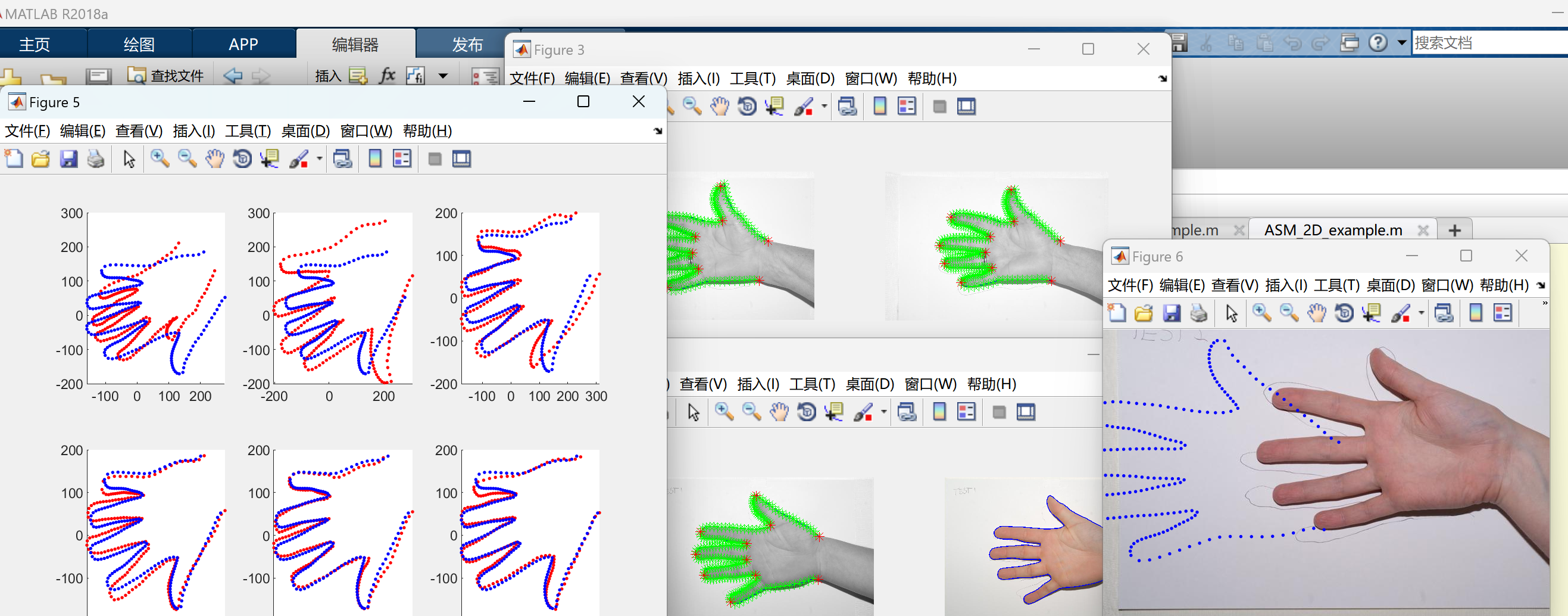
【图像分割和识别】活动形状模型 (ASM) 和活动外观模型 (AAM)(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

HTML基础介绍2
表单格式化 ctrld:复制选中行数的所有代码 ctrlx:删除代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>表单综合案例</title> </head> <body> <!--…...
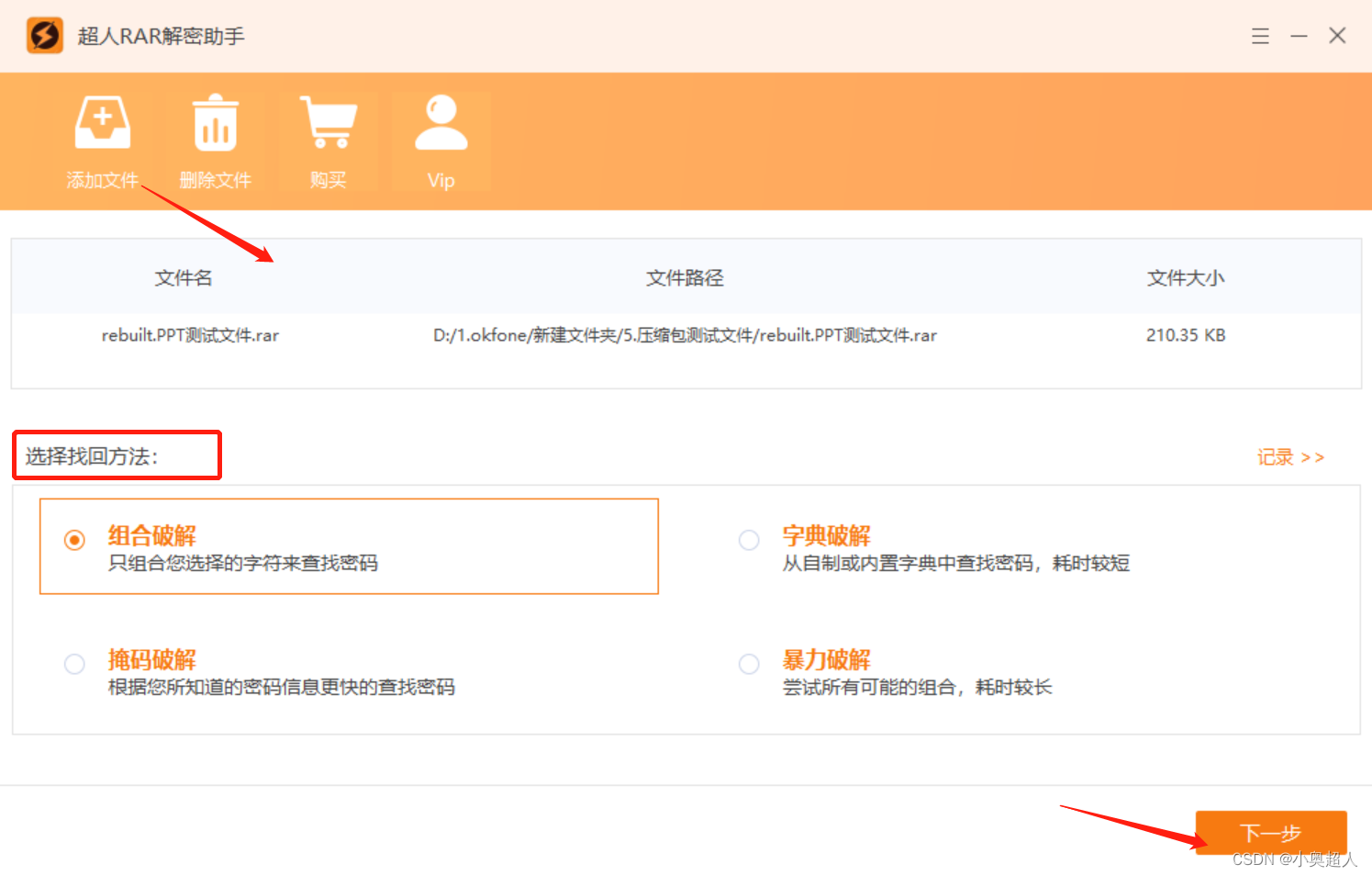
rar压缩包怎么改成zip格式
不知道大家有没有遇到需要转换压缩包格式的问题,今天想和大家分享rar压缩包改成zip格式的方法。 方法一: 直接修改rar压缩包的后缀名变为zip,就可以修改压缩包文件格式了 方法二: 先将rar压缩包解压出来,然后再将解…...

Mac 补丁管理
Mac 补丁管理涉及通过扫描收集所有缺失补丁的完整列表、下载缺失的补丁、在非生产计算机上测试它们,最后将它们推广到生产环境中进行部署来管理 macOS 端点,修补 Mac 设备(又称 Mac 修补)可增强 macOS 环境的安全级别。 什么是 m…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
