Node=>Express中间件 学习3
1.概念:

例:在处理污水的时候,一般都要经过三个处理环节,从而保证处理过后的废水,达到排放标准
处理污水的这三个中间处理环节,就可以叫中间件
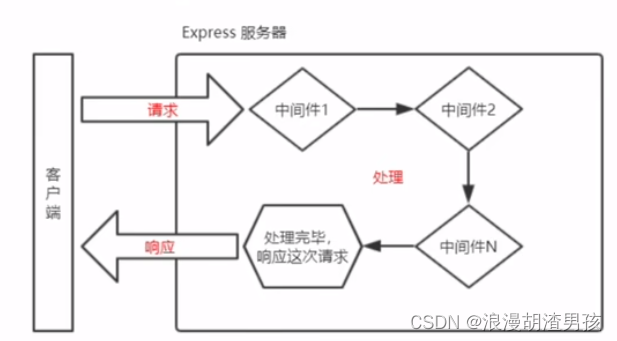
2.中间件调用流程
当一个请求到达Express的服务器之后,可以连续调用多个中间件,从而对这次请求进行预处理
3.express的中间件,本质上就是一个function处理函数,express中间件的格式如下:
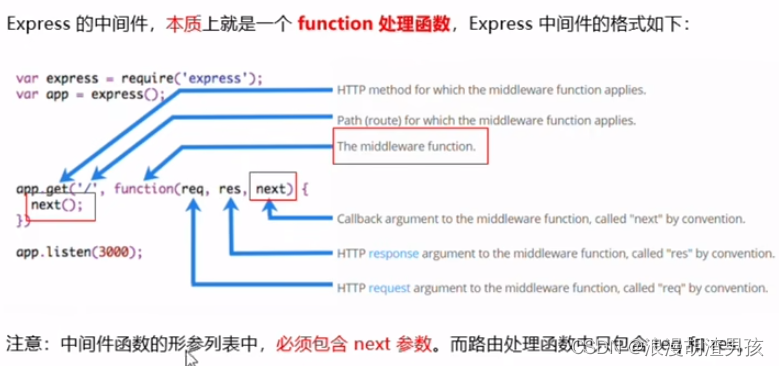
注:中间件函数的形参列表中,必须包含next参数,而路由处理函数中只包含req和res
4.next函数的作用
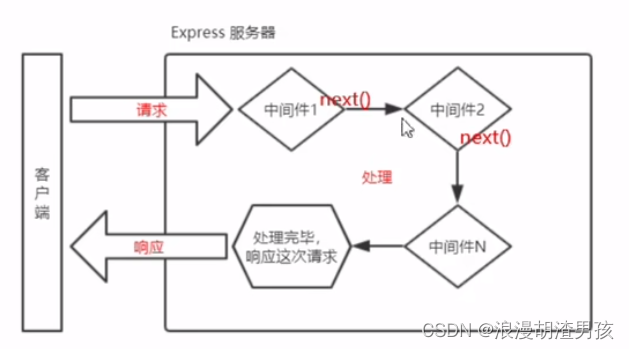
next函数是实现多个中间件连续调用的关键,他表示把流转关系转交给下一个中间件或路由
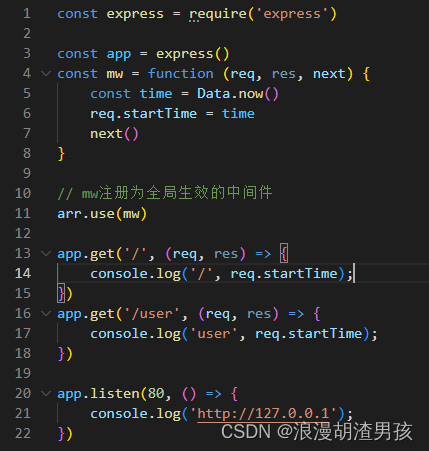
5.定义中间件函数
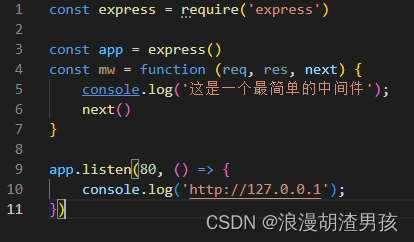
6.全局生效的中间件
客户端发起的任何请求,到达服务器之后,都会触发的中间件,叫做全局生效的中间件 调用app.use(中间件函数),即可定义一个全局生效的中间件
7.中间件的作用
多个中间件之间,共享同一份req和res,基于这样的特性,我们可以在上游的中间件,统一为req和res对象添加自定义的属性和方法,供下游的中间件或路由进行使用
8.定义多个全局中间件
连续使用app.use()定义全局中间件,执行顺序按照定义顺序
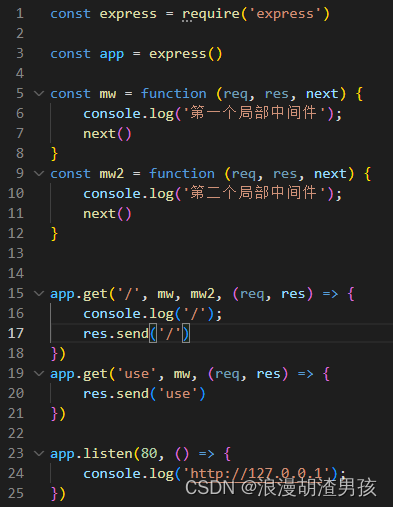
9.局部生效的中间件
不使用app.use()定义的中间件,叫做局部生效的中间件
10.中间件使用注意事项
- 中间件要在路由之前注册
- 客户端发送过来的请求,可以连续调用多个中间件进行处理
- 执行完中间件的业务代码之后,不要忘记调用next()函数
- 为了防止逻辑代码混乱,调用next()后不要再写额外的代码
- 连续调用多个中间件时,多个中间件之间,共享req和res对象
相关文章:
Node=>Express中间件 学习3
1.概念: 例:在处理污水的时候,一般都要经过三个处理环节,从而保证处理过后的废水,达到排放标准 处理污水的这三个中间处理环节,就可以叫中间件 2.中间件调用流程 当一个请求到达Express的服务器之后&#x…...
【STM32笔记】HAL库UART串口配置及重定向(解决接收中断与scanf不能同时工作的问题)
【STM32笔记】HAL库UART串口配置及重定向(解决接收中断与scanf不能同时工作的问题) 首先 要使用printf和scanf 必不可少的就是 #include <stdio.h>这里需要做的就是配置单片机的UART 并且使其能够被printf和scanf调用 打开异步工作模式 并且选择…...

【前端CSS面试题】2023前端最新版css模块,高频15问
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:博主收集的CSS面试题 目录 一、CSS必备面试题 1.CSS3新特性 2.CSS实现元素两个盒子垂…...

Linux命令大全,赶紧收藏!
新的一年 新的征程 新的课程开班 等你来学! 本文为Linux命令大全,从A到Z都有总结,建议大家收藏以便查用,或者查漏补缺! A 命令 描述 access 用于检查调用程序是否可以访问指定的文件,用于检查文件…...

大数据入门怎么学习
大数据学习不能停留在理论的层面上,大数据方向切入应是全方位的,基础语言的学习只是很小的一个方面,编程落实到最后到编程思想。学习前一定要对大数据有一个整体的认识。 大数据是数据量多吗?其实并不是,通过Hadoop其…...
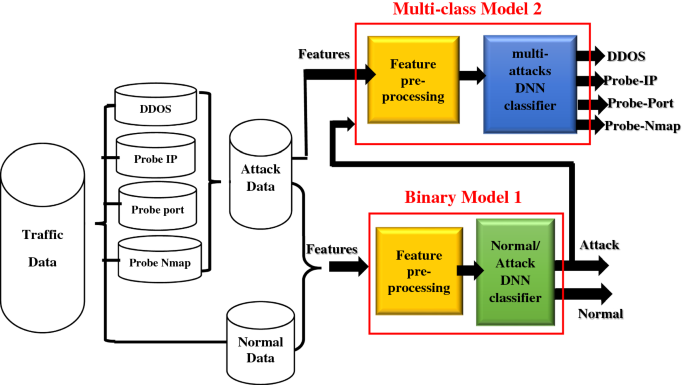
用于异常检测的深度神经网络模型融合
用于异常检测的深度神经网络模型融合 在当今的数字时代,网络安全至关重要,因为全球数十亿台计算机通过网络连接。近年来,网络攻击的数量大幅增加。因此,网络威胁检测旨在通过观察一段时间内的流量数据来检测这些攻击,…...

游戏服务器如何选择合适的服务器配置
游戏服务器如何选择合适的服务器配置 大家好,今天给大家分享一下游戏服务器配置的选择,为什么特别的说明一下服务器呢?服务器是决定服稳定性和安全性最重要的一个程序,如果是服务器配置不够,可能会导致服掉线、卡顿的…...
01-幂等性解释,问题及常用解决方案
目录 1. 幂等性简介 2. 后端如何解决幂等性问题 2.1 数据库层面 -> 2.1.1 防重表 -> 2.1.2 数据库悲观锁(不建议,容易出现死锁情况) -> 2.1.3 数据库乐观锁 -> 2.1.4 乐观锁CAS算法原理 2.2 锁层面 2.3 幂等性token层面 -> 2.3.1 简介文字描述: …...

SpringBoot配置文件
配置文件有两种格式: .properties .yml .properties是老版配置文件,.yml是新版配置文件 一、properties详解 IDEA社区版不支持 properties格式的日志的提示,需要安装相应插件。 3.1properties 基本语法 (ps:小技巧࿰…...

基于蜣螂算法改进的DELM分类-附代码
蜣螂算法改进的深度极限学习机DELM的分类 文章目录蜣螂算法改进的深度极限学习机DELM的分类1.ELM原理2.深度极限学习机(DELM)原理3.蜣螂算法4.蜣螂算法改进DELM5.实验结果6.参考文献7.Matlab代码1.ELM原理 ELM基础原理请参考:https://blog.c…...
FPGA纯verilog代码实现图像对数变换,提供工程源码和技术支持
目录1、图像对数变换理论2、log系数的matlab生成3、FPGA实现图像对数变换4、vivado与matlab联合仿真5、vivado工程介绍6、上板调试验证并演示7、福利:工程代码的获取1、图像对数变换理论 对数变换可以将图像的低灰度值部分扩展,显示出低灰度部分更多的细…...

【Python百日进阶-Web开发-Vue3】Day516 - Vue+ts后台项目3:首页
文章目录 一、首页头部1.1 element-plus中找到适合的Container布局容器1.2 头部容器Layout 布局1.3 src/views/HomeView.vue二、侧边菜单栏2.1 element-plus中找到适合的Menu侧栏2.2 src/views/HomeView.vue三、侧边栏的动态路由3.1 src/views/HomeView.vue3.2 src/views/Goods…...
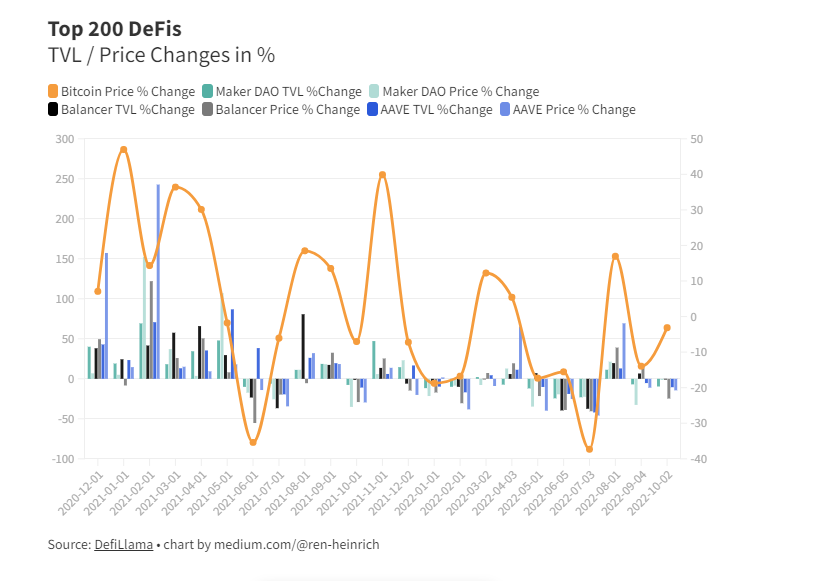
分析了 200 个 DeFi 项目,我发现了这些规律
作者:Ren & Heinrich翻译:dongdong在这篇文章中,我分享了我通过分析当前排名前 200 的 DeFi 加密项目的见解。这不是一项学术研究。尽管如此,这些发现对加密货币投资者来说具有附加值。我使用 https://defillama.com/ 的公共数…...

你领证了吗?各地2022下半年软考纸质证书发放中
不少同学都在关注2022下半年软考证书领取时间,截止至目前,江苏、南京、山东、浙江、贵州、云南、大连、广西地区的纸质证书可以领取了,请大家在证书申领时间内及时预约证书邮寄发放哦~ 江苏 证书领取时间:2023年2月3日起 南京 …...
将群晖NAS变为本地盘
本文介绍一个工具,可以在 Windows 系统下将群晖NAS的目录变为本地盘,好处是在外部访问的时候,能够大大改善体验。可以用本地的应用程序直接打开,速度依赖网络带宽,正常情况下,看视频是没有问题的。当然&…...

以太坊上交易异常Pending的处理方法
交易Pending ETH交易pending的原因: 1.交易GasPrice设置过低,共识节点不打包 2.账户Nonce不连续,一直处于交易池队列当中 只要确认了是哪种原因引起的,就可以做出对应的解决方案。 GasPrice设置过低 由于ETH共识节点是按照Gas价格从高到低打包交易,如果每笔交易的GasPr…...

第三节 第一个内核模块
hellomodule 实验 实验说明 硬件介绍 本节实验使用到STM32MP157 开发板 实验代码讲解 本章的示例代码目录为:linux_driver/module/hellomodule 从前面我们已经知道了内核模块的工作原理,这一小节就开始写代码了,跟hello world 一样&…...
从CNN到Transformer:基于PyTorch的遥感影像、无人机影像的地物分类、目标检测、语义分割和点云分类
我国高分辨率对地观测系统重大专项已全面启动,高空间、高光谱、高时间分辨率和宽地面覆盖于一体的全球天空地一体化立体对地观测网逐步形成,将成为保障国家安全的基础性和战略性资源。随着小卫星星座的普及,对地观测已具备多次以上的全球覆盖…...

操作系统的奋斗(三)内存管理
第三章 内存管理3.1内存管理概念3.1.1 内存管理的基本原理和要求(1)内存管理的主要功能3.1.2 覆盖和交换(1)覆盖(2)交换3.1.3 连续分配管理方式(1)单一连续分配(2&#x…...

多选多的一种通用处理逻辑
开发的时候,我们经常会涉及元素的多选多,并且还需要对选中的元素进行拖动排序 通用的设计方案如下 游戏资源集合与游戏资源的绑定关系处理(多选多的一种通用处理逻辑) 可能的情况: 1.之前被选中的资源,现…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...