常见的相似性度量方法
有如下几种计算相似性方法:
点积相似度
X ⋅ Y = ∣ X ∣ ∣ Y ∣ c o s θ = ∑ i = 1 n x i ∗ y i \begin{aligned} X \cdot Y &= |X||Y|cos\theta \\ &= \sum_{i=1}^n x_i * y_i \end{aligned} X⋅Y=∣X∣∣Y∣cosθ=i=1∑nxi∗yi
向量内积的结果是没有界限的,解决办法就是先归一化再相乘,就是下面的余弦相似度了。
余弦相似度
X ⋅ Y = ∑ i = 1 n x i ∗ y i ∑ i = 1 n ( x i ) 2 ∗ ∑ i = 1 n ( x i ) 2 X \cdot Y = \frac{\sum_{i=1}^n x_i * y_i}{\sqrt{\sum_{i=1}^n (x_i)^2} * {\sum_{i=1}^n (x_i)^2}} X⋅Y=∑i=1n(xi)2∗∑i=1n(xi)2∑i=1nxi∗yi
余弦相似度衡量两个向量在方向上的相似性,并不关注两个向量的实际长度,即对绝对数据不敏感。
示例
用户对内容评分,5分制。A和B两个用户对两个商品的评分分别为A:(1,2)和B:(4,5)。使用余弦相似度得出的结果是0.98,看起来两者极为相似,但从评分上看A不喜欢这两个东西,而B比较喜欢。造成这个现象的原因就在于,余弦相似度没法衡量每个维数值的差异,对数值的不敏感导致了结果的误差。
需要修正这种不合理性,就出现了调整余弦相似度,即所有维度上的数值都减去一个均值。
比如A和B对两部电影评分的均值分别是(1+4)/2=2.5,(2+5)/2=3.5。那么调整后为A和B的评分分别是:(-1.5,-1.5)和(1.5,2.5),再用余弦相似度计算,得到-0.98,相似度为负值,显然更加符合现实。
注:为什么是在所有用户对同一物品的打分上求均值,每个人打分标准不一,对所有用户求均值,等于是所有用户的打分映射到了同一空间内。上述是在计算两个用户的相似度,以此类推计算两个物品的相似度,就要计算所有物品的均值了。
修正的余弦相似度可以说就是对余弦相似度进行归一化处理的算法,公式如下:
s ( A , B ) = ∑ i ∈ I ( R A , i − R i ˉ ) ( R B , i − R i ˉ ) ∑ i ∈ I ( R A , i − R i ˉ ) 2 ∑ i ∈ I ( R B , i − R i ˉ ) 2 s(A, B)=\frac{\sum_{i \in I}\left(R_{A, i}-\bar{R_i}\right)\left(R_{B, i}-\bar{R_i}\right)}{\sqrt{\sum_{i \in I}\left(R_{A, i}-\bar{R_i}\right)^2} \sqrt{\sum_{i \in I}\left(R_{B, i}-\bar{R_i}\right)^2}} s(A,B)=∑i∈I(RA,i−Riˉ)2∑i∈I(RB,i−Riˉ)2∑i∈I(RA,i−Riˉ)(RB,i−Riˉ)
R A , i R_{A,i} RA,i 表示用户A在商品i上的打分, R i ˉ \bar{R_i} Riˉ表示商品i在所有用户上的打分均值。
皮尔逊相关系数
Pearson 相关系数是用来检测两个连续型变量之间线性相关的程度,它解决了余弦相似度会收到向量平移影响的问题。取值范围为 [−1,1],正值表示正相关,负值表示负相关,绝对值越大表示线性相关程度越高:
ρ x , y = cov ( x , y ) σ x σ y = E [ ( x − μ x , y − μ y ) ] σ x σ y = ∑ i ( x i − x ˉ ) ( y i − y ˉ ) ∑ i ( x i − x ˉ ) 2 ∑ i ( y i − y ˉ ) 2 \begin{aligned} \rho_{\boldsymbol{x}, \boldsymbol{y}} &= \frac{\operatorname{cov}(\boldsymbol{x}, \boldsymbol{y})}{\sigma_{\boldsymbol{x}} \sigma_{\boldsymbol{y}}} \\ &= \frac{E\left[\left(\boldsymbol{x}-\mu_{\boldsymbol{x}}, \boldsymbol{y}-\mu_{\boldsymbol{y}}\right)\right]}{\sigma_{\boldsymbol{x}} \sigma_{\boldsymbol{y}}} \\ &= \frac{\sum_i\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_i\left(x_i-\bar{x}\right)^2} \sqrt{\sum_i\left(y_i-\bar{y}\right)^2}} \end{aligned} ρx,y=σxσycov(x,y)=σxσyE[(x−μx,y−μy)]=∑i(xi−xˉ)2∑i(yi−yˉ)2∑i(xi−xˉ)(yi−yˉ)
如果把 x ′ = x − x ˉ , y ′ = y − y ˉ x'=x-\bar{x}, y'=y-\bar{y} x′=x−xˉ,y′=y−yˉ ,那么皮尔逊系数计算的就是 x ′ 和 y ′ x' 和 y' x′和y′ 的余弦相似度。
参考
- 点积相似度、余弦相似度、欧几里得相似度
- 常用的特征选择方法之 Pearson 相关系数
- 图片向量相似检索服务(2)——四种基本距离计算原理
- 这篇博客倒是很简洁,适合速读
- 点积相似度、余弦相似度、欧几里得相似度
- 相似性和距离度量 (Similarity & Distance Measurement)
相关文章:

常见的相似性度量方法
有如下几种计算相似性方法: 点积相似度 X ⋅ Y ∣ X ∣ ∣ Y ∣ c o s θ ∑ i 1 n x i ∗ y i \begin{aligned} X \cdot Y & |X||Y|cos\theta \\ & \sum_{i1}^n x_i * y_i \end{aligned} X⋅Y∣X∣∣Y∣cosθi1∑nxi∗yi 向量内积的结果是没…...

Day06-JS高级编程
Day01-JS高级编程 一 变量和常量 1 概念 在程序中,变量是值可以改变的量,常量是值不可以改变的量 在ES6以前变量的创建使用var关键字 (可以创建多个同名变量) 从ES6开始变量的创建推荐使用let关键字 (不可以创建多个同名变量) 从ES6开始常量的创建使用const关键 (不可以创建…...
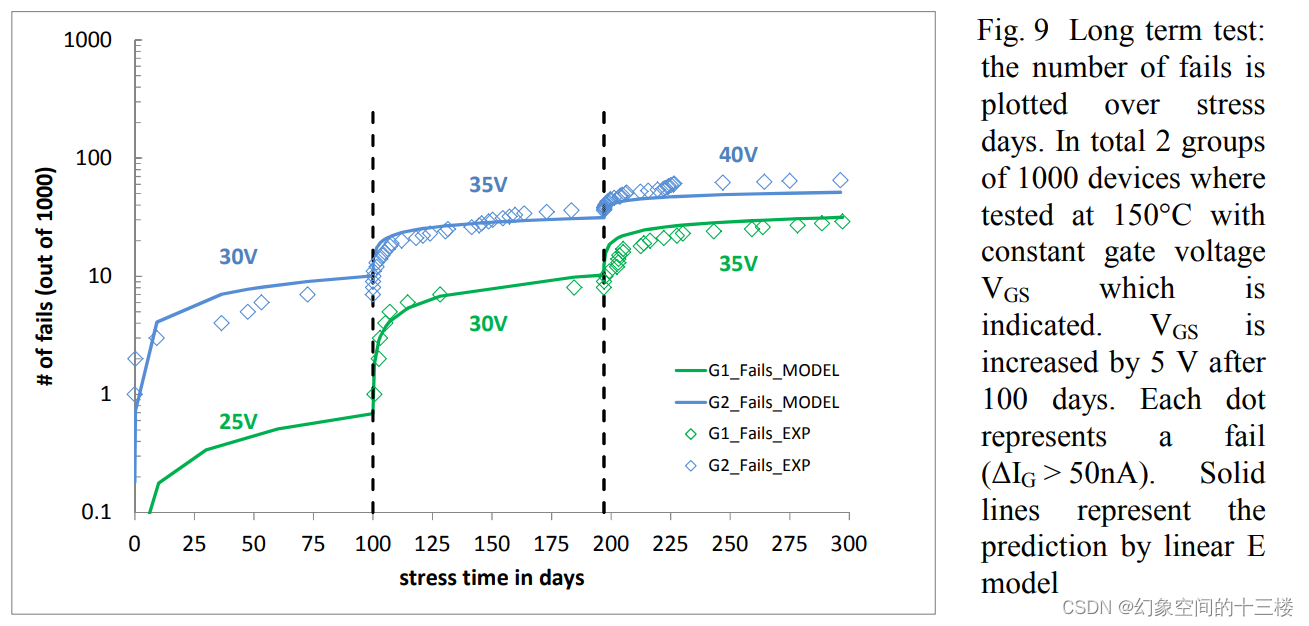
针对高可靠性和高性能优化的1200V硅碳化物沟道MOSFET
目录 标题:1200V SiC Trench-MOSFET Optimized for High Reliability and High Performance摘要信息解释研究了什么文章创新点文章的研究方法文章的结论 标题:1200V SiC Trench-MOSFET Optimized for High Reliability and High Performance 摘要 本文详…...

开发框架软件公司:与之携手,共同开启办公流程化之路!
在快节奏的社会里,如何提高企业的办公效率?如何让各部门之间的协作关系更为顺畅?如何把企业内部的数据真正利用起来,成为高层做出经营决策的重要依据?其实,要做到这些,与开发框架软件公司联手合…...

openCV C++环境配置
文章目录 一、openCV 安装二、新建项目三、配置环境变量四、测试使用 编译器:vs2017 OpenCV:4.5.4 一、openCV 安装 将openCV安装到一个路径下,我安装到了D盘根目录下 二、新建项目 在vs2017新建控制台空项目,打开项目属性 在VC目录 -> 包含目录下…...
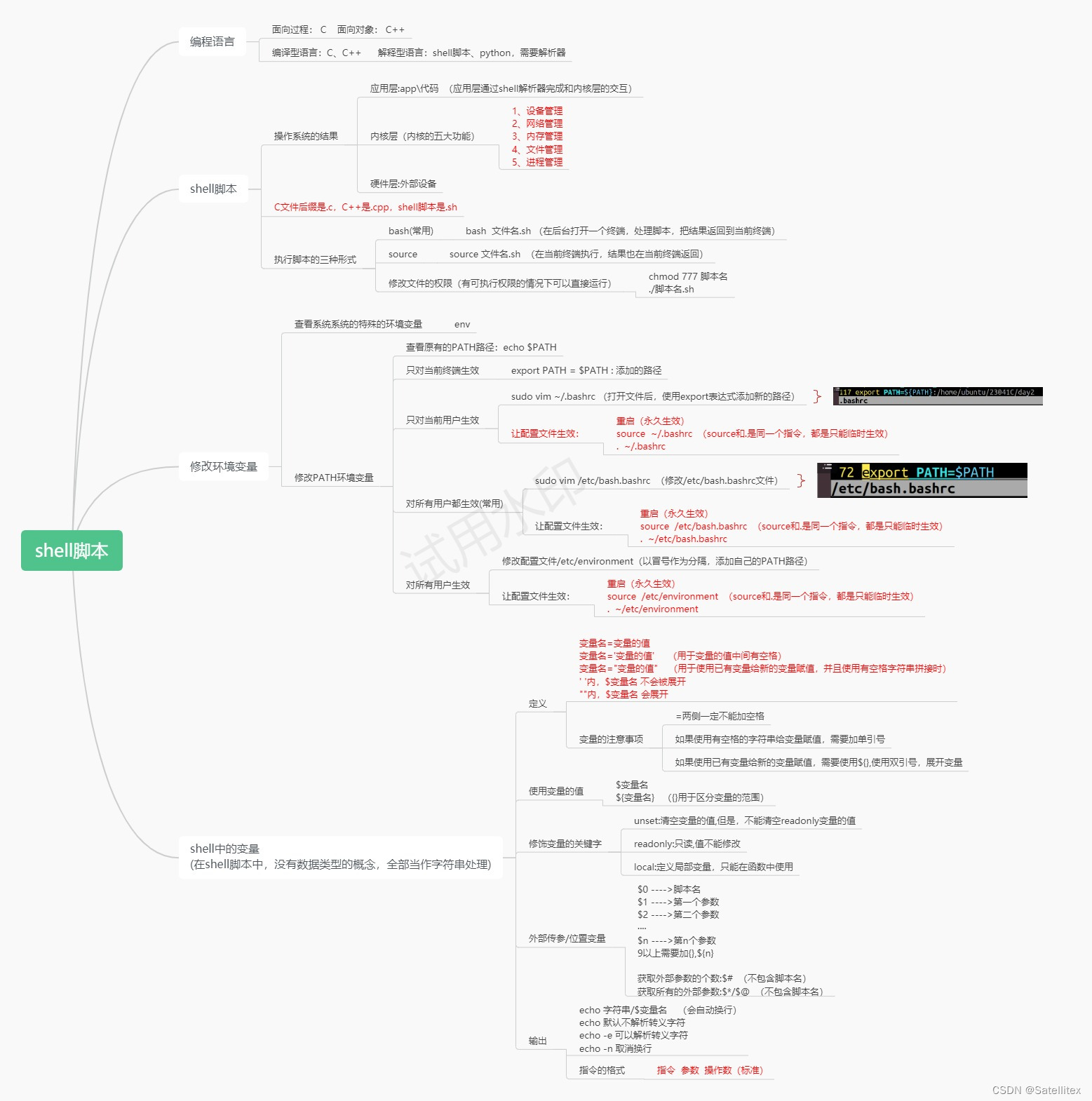
8.3 作业 c高级
1.递归实现,输入一个数,输出这个数的每一位: #include<myhead.h>void print_digit(int num) {if(num<10){printf("%d",num);puts("");}else{print_digit(num/10); //递归打印除最后一位外的数printf("%…...
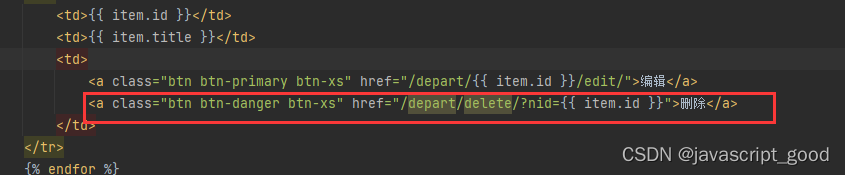
django实现部门表的增删改查界面
1、前期准备 部署好mysql数据库,创建好unicom数据库下载好bootstap的插件下载好jquery的插件下载好mysqlclient-1.4.6-cp36-cp36m-win_amd64.whl的安装包,根据python的版本下载 2、创建项目 在pycharm中创建项目 在pycharm的终端创建虚拟环境 py -m v…...
Tomcat的介绍和安装配置、eclipse中动态web项目的创建和运行、使用IDEA创建web项目并运行
一、Tomcat的介绍和安装配置 安装tomcat: 环境变量的配置: 配置之后重启cmd,执行startup命令,启动tomcat 在localhost:8080,能进入tomcat主界面,说明配置成功 二、eclipse中动态web项目的创建和运行 tomca…...
idea操作——已经push到远程的代码回滚(不保留本地更改)
1. git: 2. 找到相应分支--->找到要回滚的代码的位置----->右键,然后选择如图的选项: 3.下图的选项选择hard,然后选择reset 4.操作完成后等一会,待同步结束后push代码到远程,选择force push.…...

无涯教程-Lua - 垃圾回收
Lua使用自动内存管理,该管理使用基于Lua内置的某些算法的垃圾回收。 垃圾收集器暂停 垃圾收集器暂停用于控制垃圾收集器之前需要等待多长时间; Lua的自动内存管理再次调用它。值小于100意味着Lua将不等待下一个周期。同样,此值的较高值将导…...

DP(各种模型)
数字三角形模型 摘花生 Hello Kitty想摘点花生送给她喜欢的米老鼠。 她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。 地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就…...

开学在即,这个超好用的中小学新生录取查询系统制作方法值得借鉴
即将开学,中小学负责招生的老师面临着新学年的招生工作。这是一项紧迫且重要的任务,需要老师们迅速而有效地应对。在新生录取过程中,有几个关键任务需要尽快完成。 首先,老师们需要录入新生的成绩信息。这包括学生的考试成绩、综…...

使用Canvas裁剪图片
使用Canvas裁剪图片 概述 在Web开发中,我们经常需要对图片进行裁剪,以满足不同尺寸需求或者实现图片的局部展示。本篇博客将带您深入了解如何使用Canvas技术来实现图片的裁剪功能。我们将通过一个实例来演示如何利用Canvas绘制图片,并通过蒙…...

JavaScript |(三)内建对象 | 数组 | string对象 | 尚硅谷JavaScript基础实战
学习来源:尚硅谷JavaScript基础&实战丨JS入门到精通全套完整版 文章目录 📚数组🐇数组介绍⭐️数组(Array)⭐️基本操作⭐️数组的字面量 🐇数组中的常用方法⭐️push()⭐️pop()⭐️unshift()⭐️shif…...
势能线段树
目录 简单介绍 题目 1. 上帝造题的七分钟 2 2.SUM and REPLACE 3. And RMQ 总结 简单介绍 题目 1. 上帝造题的七分钟 2 链接:https://www.luogu.com.cn/problem/P4145 维护两种操作 1.区间开根号(下取整) 2.区间和询问 显然无法通过懒标记来计算区间开根号…...

【phaser微信抖音小游戏开发004】往画布上增加文本以及文本的操作
我们在states中创建st004.js的类,或者将states中的index.js直接重命名为st004.js,把里面的类名也修改为st004.如下图 在main.js中,引入st004,并设置启用的state为st004。如下图 接下来到states/st004里面,在create里面将文本修改一…...
【1.4】Java微服务:服务注册和调用(Eureka和Ribbon实现)
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: 微服务 ✨特色专栏: 知识分享 &#x…...

QT中使用ffmpeg的api进行视频的播放
在了解ffmpeg使用api进行视频的播放之前,我们首先了解一下视频的播放流程。 一、视频的播放流程 首先是我们最常见的视频文件,在播放流程中首先是要打开视频文件,将视频文件中的数据进行解封装,之后再将解封装之后的视频进行解码…...
使用idea实现git操作大全(在项目开发中遇到的实际情况
使用idea实现git操作大全(在项目开发中遇到的实际情况) 1.安装git插件2.在开发中切记拉一个自己的分支 1.安装git插件 2.在开发中切记拉一个自己的分支 选中需要拉的分支,右键该分支,选中new breach from “分支”,点…...

SQL面试题:一个优化案例
问题描述 假如存在以下两个表: CREATE TABLE customer ( C_CUSTKEY int NOT NULL, C_NAME varchar(25) NOT NULL, C_ADDRESS varchar(40) NOT NULL, C_NATIONKEY int NOT NULL, C_PHONE char(15) NOT NULL, C_ACCTBAL decimal(15,2) NOT NULL, C_MKTSEGMENT char(…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
