势能线段树
目录
简单介绍
题目
1. 上帝造题的七分钟 2
2.SUM and REPLACE
3. And RMQ
总结
简单介绍

题目
1. 上帝造题的七分钟 2
链接:https://www.luogu.com.cn/problem/P4145
维护两种操作
1.区间开根号(下取整)
2.区间和询问
显然无法通过懒标记来计算区间开根号后的值,其由叶子结点本身的值决定。容易发现当一个数连续进行开根号操作会在很少的次数变为1,且值不再改变,1即为零势能点。因此我们可以维护区间max。一旦区间修改时发现此区间的max<=1时,我们不需要再次修改,直接return即可,否则向下递归修改。
Code:
#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>
#define endl "\n"
#define int long long
const int N=1e5+10;
struct segment_tree {int a[N];struct node {int l,r;int mx,sum;}tr[N<<2];void build(int u,int l,int r) {tr[u].l=l,tr[u].r=r;if(l==r) {tr[u].mx=tr[u].sum=a[l];return ;}int mid=(l+r)>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushup(u);} void modify(int u,int l,int r) {if(tr[u].mx<=1) return ;if(tr[u].l==tr[u].r) {tr[u].mx=sqrt(tr[u].mx);tr[u].sum=tr[u].mx;return ;}int mid=(tr[u].l+tr[u].r)>>1;if(l<=mid) modify(u<<1,l,r);if(r>mid) modify(u<<1|1,l,r);pushup(u);} int query(int u,int l,int r) {if(tr[u].l>=l&&tr[u].r<=r) {return tr[u].sum;}int mid=(tr[u].l+tr[u].r)>>1;int res=0;if(l<=mid) res+=query(u<<1,l,r);if(r>mid) res+=query(u<<1|1,l,r);return res;}void pushup(int u) {tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;tr[u].mx=max(tr[u<<1].mx,tr[u<<1|1].mx);}
}ST;
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n,m;cin>>n;for(int i=1;i<=n;i++) cin>>ST.a[i];ST.build(1,1,n);cin>>m;while(m--) {int op,l,r;cin>>op>>l>>r;if(l>r) swap(l,r);if(op==0) ST.modify(1,l,r);else cout<<ST.query(1,l,r)<<endl; }
}2.SUM and REPLACE
链接:https://codeforces.com/contest/920/problem/F
定义f(x)为x因子的数量
维护三种操作
1.区间修改x=f(x)
2.区间和查询
手动模拟f(x)可以发现,进行f(x)操作,数值单调不增,且x<=2时,其值不在改变,因此同上题一样维护区间最大值即可。f(x)可以O(nlogn)时间预处理出来。
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<map>
#include<set>
using namespace std;
#define PII pair<int,int>
#define endl "\n"
#define int long long
const int N=3e5+10,M=1e6+10;
int d[M+1];
struct segment_tree {int a[N];struct node {int l,r;int mx,sum;}tr[N<<2];void build(int u,int l,int r) {tr[u].l=l,tr[u].r=r;if(l==r) {tr[u].mx=tr[u].sum=a[l];return ;}int mid=(l+r)>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushup(u);} void modify(int u,int l,int r) {if(tr[u].mx<=2) return ;if(tr[u].l==tr[u].r) {tr[u].mx=d[tr[u].mx];tr[u].sum=tr[u].mx;return ;}int mid=(tr[u].l+tr[u].r)>>1;if(l<=mid) modify(u<<1,l,r);if(r>mid) modify(u<<1|1,l,r);pushup(u);} int query(int u,int l,int r) {if(tr[u].l>=l&&tr[u].r<=r) {return tr[u].sum;}int mid=(tr[u].l+tr[u].r)>>1;int res=0;if(l<=mid) res+=query(u<<1,l,r);if(r>mid) res+=query(u<<1|1,l,r);return res;}void pushup(int u) {tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;tr[u].mx=max(tr[u<<1].mx,tr[u<<1|1].mx);}
};
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);for(int i=1;i<=M;i++) { //预处理for(int j=i;j<=M;j+=i) {d[j]++;}}int n,m;cin>>n>>m;segment_tree ST;for(int i=1;i<=n;i++) cin>>ST.a[i];ST.build(1,1,n);while(m--) {int op,l,r;cin>>op>>l>>r;if(op==1) ST.modify(1,l,r);else cout<<ST.query(1,l,r)<<endl;}
}3. And RMQ
链接:
维护三个操作
1.区间按位与x
2.区间最大值
3.单点修改
这题零势能点藏得较深,我们考虑将x二进制展开,发现在x的二进制位为零的位置,区间所有数的二进制位也为零,则操作可以忽略。维护区间或
当 orsum & x =orsum,则直接return
Code:
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<map>
#include<set>
using namespace std;
#define PII pair<int,int>
#define endl "\n"
const int N=4e5+10;
struct segment_tree {int a[N];struct node {int l,r;int mx,sum;}tr[N<<2];void build(int u,int l,int r) {tr[u].l=l,tr[u].r=r;if(l==r) {tr[u].mx=tr[u].sum=a[l];return ;}int mid=(l+r)>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushup(u);} void modify(int u,int l,int r,int x) {if((tr[u].sum&x)==tr[u].sum) return ;if(tr[u].l==tr[u].r) {tr[u].mx=tr[u].mx&x;tr[u].sum=tr[u].mx;return ;}int mid=(tr[u].l+tr[u].r)>>1;if(l<=mid) modify(u<<1,l,r,x);if(r>mid) modify(u<<1|1,l,r,x);pushup(u);} int query(int u,int l,int r) {if(tr[u].l>=l&&tr[u].r<=r) {return tr[u].mx;}int mid=(tr[u].l+tr[u].r)>>1;int res=0;if(l<=mid) res=max(res,query(u<<1,l,r));if(r>mid) res=max(res,query(u<<1|1,l,r));return res;}void update(int u,int k,int x) {if(tr[u].l==tr[u].r) {tr[u].mx=tr[u].sum=x;return ;}int mid=(tr[u].l+tr[u].r)>>1;if(k<=mid) update(u<<1,k,x);else update(u<<1|1,k,x);pushup(u);}void pushup(int u) {tr[u].sum=tr[u<<1].sum|tr[u<<1|1].sum;tr[u].mx=max(tr[u<<1].mx,tr[u<<1|1].mx);}
}ST;
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>ST.a[i];ST.build(1,1,n);while(m--) {int l,r,x;string op;cin>>op;if(op=="AND") {cin>>l>>r>>x;ST.modify(1,l,r,x);}else if(op=="UPD") {cin>>l>>x;ST.update(1,l,x);}else {cin>>l>>r;cout<<ST.query(1,l,r)<<endl;}}
}总结
1.对于区间修改操作,修改操作会使得值在趋向零势能点前严格单调减少,在变为零势能点后不在变化。需要维护一个值来界定是否到达零势能
2.且题目不能出现其他非单调的区间修改操作,如区间加,区间乘等。如果有其他修改操作,可以通过构造形如 update1 ,update 2,update 1,update 2 的数据破坏单调性,从而使操作1复杂度变为暴力修改的O(nlogn)
相关文章:
势能线段树
目录 简单介绍 题目 1. 上帝造题的七分钟 2 2.SUM and REPLACE 3. And RMQ 总结 简单介绍 题目 1. 上帝造题的七分钟 2 链接:https://www.luogu.com.cn/problem/P4145 维护两种操作 1.区间开根号(下取整) 2.区间和询问 显然无法通过懒标记来计算区间开根号…...

【phaser微信抖音小游戏开发004】往画布上增加文本以及文本的操作
我们在states中创建st004.js的类,或者将states中的index.js直接重命名为st004.js,把里面的类名也修改为st004.如下图 在main.js中,引入st004,并设置启用的state为st004。如下图 接下来到states/st004里面,在create里面将文本修改一…...
【1.4】Java微服务:服务注册和调用(Eureka和Ribbon实现)
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: 微服务 ✨特色专栏: 知识分享 &#x…...

QT中使用ffmpeg的api进行视频的播放
在了解ffmpeg使用api进行视频的播放之前,我们首先了解一下视频的播放流程。 一、视频的播放流程 首先是我们最常见的视频文件,在播放流程中首先是要打开视频文件,将视频文件中的数据进行解封装,之后再将解封装之后的视频进行解码…...
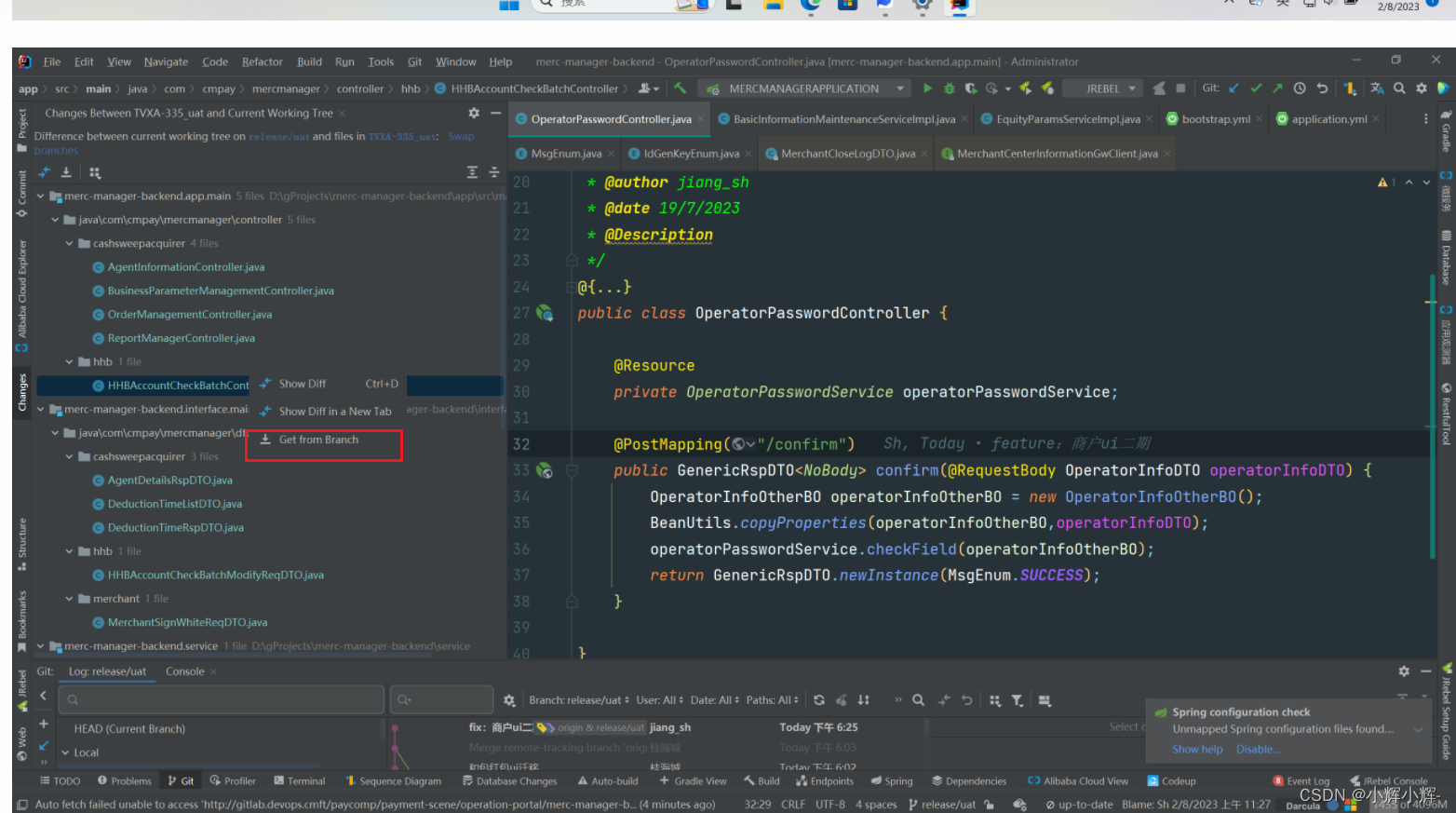
使用idea实现git操作大全(在项目开发中遇到的实际情况
使用idea实现git操作大全(在项目开发中遇到的实际情况) 1.安装git插件2.在开发中切记拉一个自己的分支 1.安装git插件 2.在开发中切记拉一个自己的分支 选中需要拉的分支,右键该分支,选中new breach from “分支”,点…...

SQL面试题:一个优化案例
问题描述 假如存在以下两个表: CREATE TABLE customer ( C_CUSTKEY int NOT NULL, C_NAME varchar(25) NOT NULL, C_ADDRESS varchar(40) NOT NULL, C_NATIONKEY int NOT NULL, C_PHONE char(15) NOT NULL, C_ACCTBAL decimal(15,2) NOT NULL, C_MKTSEGMENT char(…...
链表的总体涵盖以及无哨兵位单链表实现——【数据结构】
😊W…Y:个人主页 在学习之前看一下美丽的夕阳,也是很不错的。 如果觉得博主的美景不错,博客也不错的话,关注一下博主吧💕 在上一期中,我们说完了顺序表,并且提出顺序表中的问题 1. 中…...
网页版Java五子棋项目(一)websocket【服务器给用户端发信息】
网页版Java五子棋项目(一)websocket【服务器给用户端发信息】 一、为什么要用websocket二、websocket介绍原理解析 三、代码演示1. 创建后端api(TestAPI)新增知识点:extends TextWebSocketHandler重写各种方法 2. 建立…...
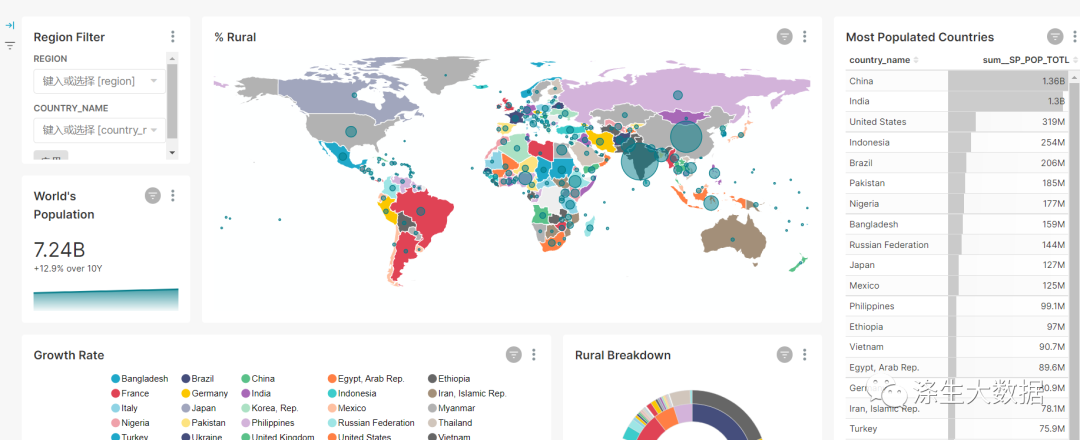
企业大数据可视化案例专题分享-入门
一、什么是数据可视化? 基本概念:数据可视化是以图示或图形格式表示的数据。让决策者可以看到以直观方式呈现的分析,以便他们可以掌握困难的概念或识别新的模式。借助交互式可视化,可以使用技术深入挖掘图表和图形以获取更多详细…...
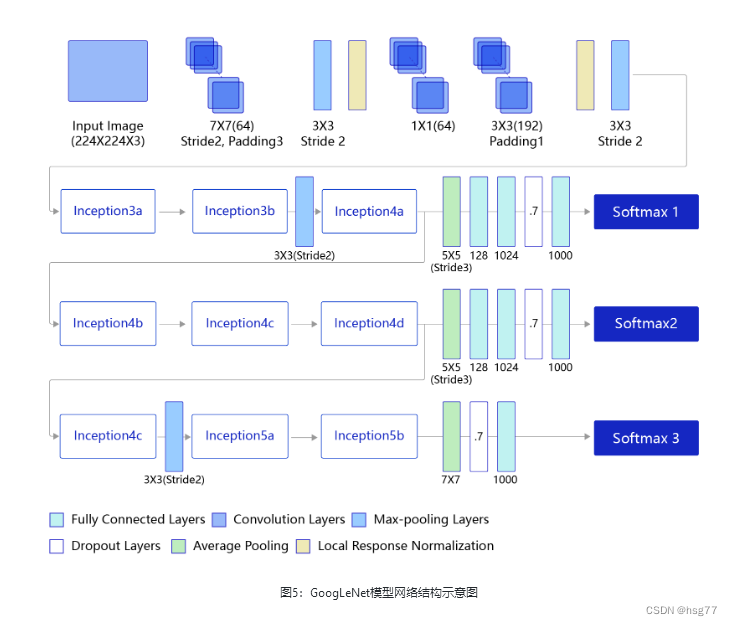
GoogLeNet卷积神经网络-笔记
GoogLeNet卷积神经网络-笔记 GoogLeNet是2014年ImageNet比赛的冠军, 它的主要特点是网络不仅有深度, 还在横向上具有“宽度”。 由于图像信息在空间尺寸上的巨大差异, 如何选择合适的卷积核来提取特征就显得比较困难了。 空间分布范围更广的…...

腾讯云TencentOS Server镜像系统常见问题解答
腾讯云TencentOS Server镜像是腾讯云推出的Linux操作系统,完全兼容CentOS生态和操作方式,TencentOS Server操作系统为云上运行的应用程序提供稳定、安全和高性能的执行环境,TencentOS可以运行在腾讯云CVM全规格实例上,包括黑石物理…...

【项目 进程13】2.28共享内存(1) 2.29共享内存(2)
文章目录 2.28共享内存(1)共享内存(效率最高,比内存映射更高。因为内存映射还需一个文件做载体)共享内存使用步骤共享内存操作函数头文件 2.29共享内存(2)共享内存相关问题共享内存和内存映射的…...

Flask框架-流量控制:flask-limiter的使用
一、flask使用flask-limiter存在版本问题 Flask1.1.4 Flask-Bootstrap3.3.7.1 Flask-Caching1.9.0 Flask-Cors3.0.10 Flask-Limiter1.4 Flask-Migrate2.5.3 Flask-RESTful0.3.8 Flask-Script2.0.6 Flask-SocketIO5.0.1 Flask-Sockets0.2.1 Flask-SQLAlchemy2.4.4 Jinjia22.11.…...
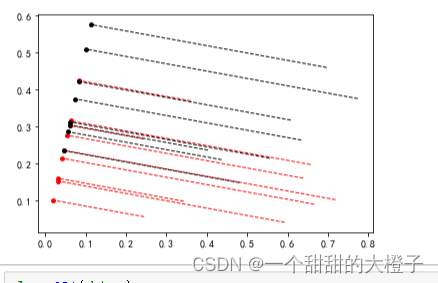
【机器学习】西瓜书习题3.5Python编程实现线性判别分析,并给出西瓜数据集 3.0α上的结果
参考代码 结合自己的理解,添加注释。 代码 导入相关的库 import numpy as np import pandas as pd import matplotlib from matplotlib import pyplot as plt导入数据,进行数据处理和特征工程 得到数据集 D { ( x i , y i ) } i 1 m , y i ∈ { 0 ,…...

Elasticsearch:通过动态修剪实现更快的基数聚合
作者:Adrien Grand Elasticsearch 8.9 通过支持动态修剪(dynamic pruning)引入了基数聚合加速。 这种优化需要满足特定的条件才能生效,但一旦实现,通常会产生惊人的结果。 我们观察到,通过此更改࿰…...

Webpack5 生产模式压缩图片ImageMinimizerPlugin
文章目录 一、 ImageMinimizerPlugin是什么?二、已经有了asset,为什么需要ImageMinimizerPlugin?三、怎么使用ImageMinimizerPlugin?四、ImageMinimizerPlugin压缩的成果 一、 ImageMinimizerPlugin是什么? 它的实际依…...

时序预测 | Matlab实现基于BP神经网络的电力负荷预测模型
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 时序预测 | Matlab实现基于BP神经网络的电力负荷预测模型 BP神经网络是一种多层的前馈神经网络,其主要的特点是:信号是前向传播的,而误差是反向传播的。B...
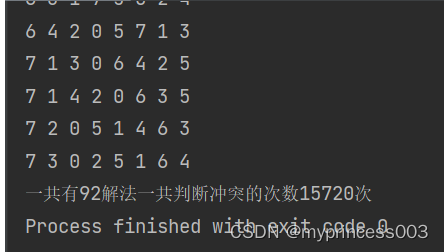
基于回溯算法实现八皇后问题
八皇后问题是一个经典的计算机科学问题,它的目标是将8个皇后放置在一个大小为88的棋盘上,使得每个皇后都不会攻击到其他的皇后。皇后可以攻击同一行、同一列和同一对角线上的棋子。 一、八皇后问题介绍 八皇后问题最早由国际西洋棋大师马克斯贝瑟尔在18…...
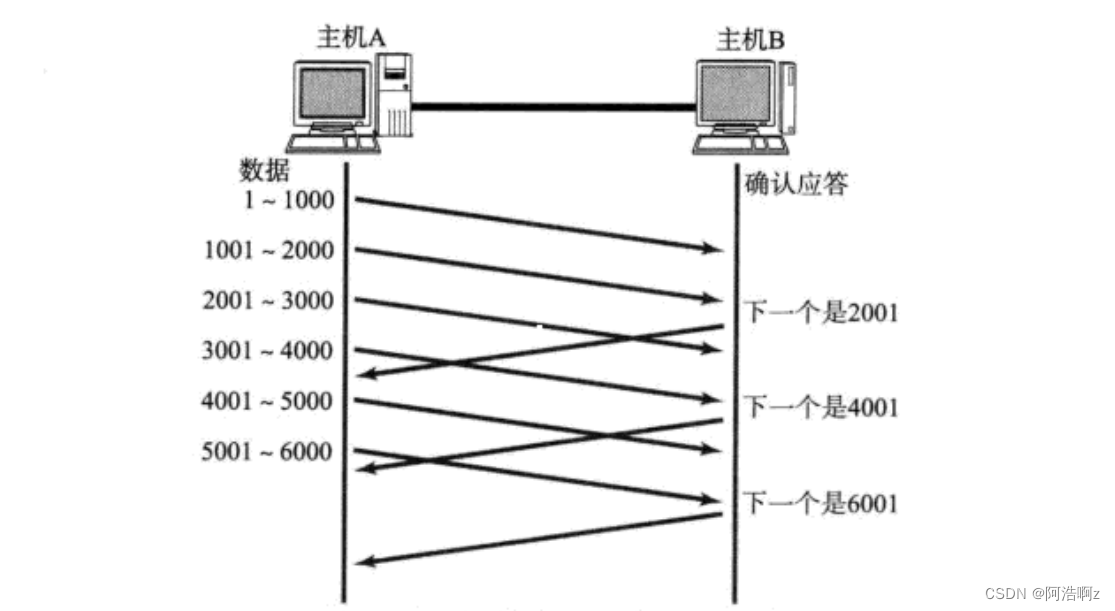
Linux【网络编程】之深入理解TCP协议
Linux【网络编程】之深入理解TCP协议 TCP协议TCP协议段格式4位首部长度---TCP报头长度信息 TCP可靠性(确认应答)&& 提高传输效率确认应答(ACK)机制32位序号与32为确认序号 16位窗口大小---自己接收缓冲区剩余空间的大小16位紧急指针---紧急数据处…...

如何克服看到别人优于自己而感到的焦虑和迷茫?
文章目录 每日一句正能量前言简述自己的感受怎么做如何调整自己的心态后记 每日一句正能量 行动是至于恐惧的良药,而犹豫、拖延,将不断滋养恐惧。 前言 虽然清楚知识需要靠时间沉淀,但在看到自己做不出来的题别人会做,自己写不出的…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
