【机器学习】西瓜书习题3.5Python编程实现线性判别分析,并给出西瓜数据集 3.0α上的结果
参考代码
结合自己的理解,添加注释。
代码
- 导入相关的库
import numpy as np
import pandas as pd
import matplotlib
from matplotlib import pyplot as plt
- 导入数据,进行数据处理和特征工程
得到数据集 D = { ( x i , y i ) } i = 1 m , y i ∈ { 0 , 1 } D=\{ (x_i,y_i) \}_{i=1}^m, y_i \in \{0,1\} D={(xi,yi)}i=1m,yi∈{0,1}
# 1.数据处理,特征工程
data_path = 'watermelon3_0_Ch.csv'
data = pd.read_csv(data_path).values
# 按照数据集3.0α,强制转换数据类型
X = data[:,7:9].astype(float)
y = data[:,9]
y[y=='是'] = 1
y[y=='否'] = 0
y = y.astype(int)
- 计算西瓜书60页中的 X i 、 μ i 、 Σ i X_{i}、\mu_i、\Sigma_i Xi、μi、Σi
# 将X的数据根据label值分成X0和X1
pos = y == 1
neg = y == 0
X0 = X[neg]
X1 = X[pos]# 计算u0,u1 keepdims保持原数据维数
u0 = X0.mean(0, keepdims=True)
u1 = X1.mean(0, keepdims=True)# 计算sigma0,sigma1
sigma0 = np.dot((X0-u0).T,X0-u0)
sigma1 = np.dot((X1-u1).T,X1-u1)
- 根据式3.33计算类内散度矩阵
S w = Σ 0 + Σ 1 = ∑ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ X 1 ( x − μ 1 ) ( x − μ 1 ) T S_w=\Sigma_0+\Sigma_1=\sum_{x\in X_{0}}(x-\mu_0)(x-\mu_0)^T+\sum_{x\in X_{1}}(x-\mu_1)(x-\mu_1)^T Sw=Σ0+Σ1=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T
根据式3.39计算 w w w
w = S w − 1 ( μ 0 − μ 1 ) w=S_w^{-1}(\mu_0-\mu_1) w=Sw−1(μ0−μ1)
# 计算类内散度矩阵 with-class scatter matrix
sw = sigma0 + sigma1# numpy.linalg.inv() 函数来计算矩阵的逆
w = np.dot(np.linalg.inv(sw),(u0-u1).T).reshape(1,-1)
- 画出样本点和得到的直线
fig, ax = plt.subplots()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['left'].set_position(('data', 0))
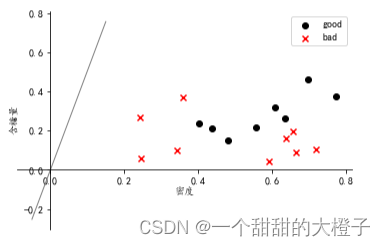
ax.spines['bottom'].set_position(('data', 0))plt.scatter(X1[:, 0], X1[:, 1], c='k', marker='o', label='good')
plt.scatter(X0[:, 0], X0[:, 1], c='r', marker='x', label='bad')plt.xlabel('密度', labelpad=1)
plt.ylabel('含糖量')
plt.legend(loc='upper right')x_tmp = np.linspace(-0.05, 0.15)
y_tmp = x_tmp * w[0, 1] / w[0, 0]
plt.plot(x_tmp, y_tmp, '#808080', linewidth=1)
得到下图
- 计算每个样本点在直线上的投影
计算的理解参考这篇文章
# 求w这个向量的 单位向量 wu
# np.linalg.norm()默认求2 范数,表示向量中各个元素平方和 的 1/2 次方,L2 范数又称 Euclidean 范数或者 Frobenius 范数。
wu = w / np.linalg.norm(w)# 正负样本点
# 求负样本的投影点,并连线
X0_project = np.dot(X0, np.dot(wu.T, wu))
plt.scatter(X0_project[:, 0], X0_project[:, 1], c='r', s=15)
for i in range(X0.shape[0]):plt.plot([X0[i, 0], X0_project[i, 0]], [X0[i, 1], X0_project[i, 1]], '--r', linewidth=1)# 求正样本的投影点,并连线
X1_project = np.dot(X1, np.dot(wu.T, wu))
plt.scatter(X1_project[:, 0], X1_project[:, 1], c='k', s=15)
for i in range(X1.shape[0]):plt.plot([X1[i, 0], X1_project[i, 0]], [X1[i, 1], X1_project[i, 1]], '--k', linewidth=1)
得到下图
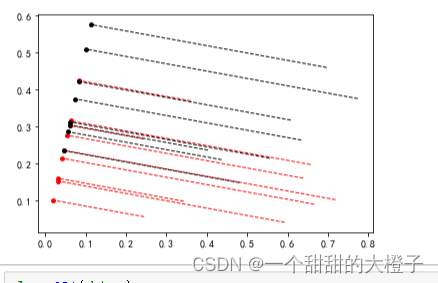
将上述代码封装成类,如下:
class LDA(object):def fit(self, X_, y_, plot_=False):pos = y_ == 1neg = y_ == 0X0 = X_[neg]X1 = X_[pos]u0 = X0.mean(0, keepdims=True) # (1, n)u1 = X1.mean(0, keepdims=True)sw = np.dot((X0 - u0).T, X0 - u0) + np.dot((X1 - u1).T, X1 - u1)w = np.dot(np.linalg.inv(sw), (u0 - u1).T).reshape(1, -1) # (1, n)if plot_:# 设置字体为楷体plt.rcParams['axes.unicode_minus']=False #用来正常显示负号plt.rcParams['font.sans-serif'] = ['KaiTi']fig, ax = plt.subplots()ax.spines['right'].set_color('none')ax.spines['top'].set_color('none')ax.spines['left'].set_position(('data', 0))ax.spines['bottom'].set_position(('data', 0))plt.scatter(X1[:, 0], X1[:, 1], c='k', marker='o', label='good')plt.scatter(X0[:, 0], X0[:, 1], c='r', marker='x', label='bad')plt.xlabel('密度', labelpad=1)plt.ylabel('含糖量')plt.legend(loc='upper right')x_tmp = np.linspace(-0.05, 0.15)y_tmp = x_tmp * w[0, 1] / w[0, 0]plt.plot(x_tmp, y_tmp, '#808080', linewidth=1)wu = w / np.linalg.norm(w)# 正负样板店X0_project = np.dot(X0, np.dot(wu.T, wu))plt.scatter(X0_project[:, 0], X0_project[:, 1], c='r', s=15)for i in range(X0.shape[0]):plt.plot([X0[i, 0], X0_project[i, 0]], [X0[i, 1], X0_project[i, 1]], '--r', linewidth=1)X1_project = np.dot(X1, np.dot(wu.T, wu))plt.scatter(X1_project[:, 0], X1_project[:, 1], c='k', s=15)for i in range(X1.shape[0]):plt.plot([X1[i, 0], X1_project[i, 0]], [X1[i, 1], X1_project[i, 1]], '--k', linewidth=1)# 中心点的投影u0_project = np.dot(u0, np.dot(wu.T, wu))plt.scatter(u0_project[:, 0], u0_project[:, 1], c='#FF4500', s=60)u1_project = np.dot(u1, np.dot(wu.T, wu))plt.scatter(u1_project[:, 0], u1_project[:, 1], c='#696969', s=60)ax.annotate(r'u0 投影点',xy=(u0_project[:, 0], u0_project[:, 1]),xytext=(u0_project[:, 0] - 0.2, u0_project[:, 1] - 0.1),size=13,va="center", ha="left",arrowprops=dict(arrowstyle="->",color="k",))ax.annotate(r'u1 投影点',xy=(u1_project[:, 0], u1_project[:, 1]),xytext=(u1_project[:, 0] - 0.1, u1_project[:, 1] + 0.1),size=13,va="center", ha="left",arrowprops=dict(arrowstyle="->",color="k",))plt.axis("equal") # 两坐标轴的单位刻度长度保存一致plt.show()self.w = wself.u0 = u0self.u1 = u1return selfdef predict(self, X):project = np.dot(X, self.w.T)wu0 = np.dot(self.w, self.u0.T)wu1 = np.dot(self.w, self.u1.T)return (np.abs(project - wu1) < np.abs(project - wu0)).astype(int)
相关文章:

【机器学习】西瓜书习题3.5Python编程实现线性判别分析,并给出西瓜数据集 3.0α上的结果
参考代码 结合自己的理解,添加注释。 代码 导入相关的库 import numpy as np import pandas as pd import matplotlib from matplotlib import pyplot as plt导入数据,进行数据处理和特征工程 得到数据集 D { ( x i , y i ) } i 1 m , y i ∈ { 0 ,…...

Elasticsearch:通过动态修剪实现更快的基数聚合
作者:Adrien Grand Elasticsearch 8.9 通过支持动态修剪(dynamic pruning)引入了基数聚合加速。 这种优化需要满足特定的条件才能生效,但一旦实现,通常会产生惊人的结果。 我们观察到,通过此更改࿰…...

Webpack5 生产模式压缩图片ImageMinimizerPlugin
文章目录 一、 ImageMinimizerPlugin是什么?二、已经有了asset,为什么需要ImageMinimizerPlugin?三、怎么使用ImageMinimizerPlugin?四、ImageMinimizerPlugin压缩的成果 一、 ImageMinimizerPlugin是什么? 它的实际依…...

时序预测 | Matlab实现基于BP神经网络的电力负荷预测模型
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 时序预测 | Matlab实现基于BP神经网络的电力负荷预测模型 BP神经网络是一种多层的前馈神经网络,其主要的特点是:信号是前向传播的,而误差是反向传播的。B...
基于回溯算法实现八皇后问题
八皇后问题是一个经典的计算机科学问题,它的目标是将8个皇后放置在一个大小为88的棋盘上,使得每个皇后都不会攻击到其他的皇后。皇后可以攻击同一行、同一列和同一对角线上的棋子。 一、八皇后问题介绍 八皇后问题最早由国际西洋棋大师马克斯贝瑟尔在18…...
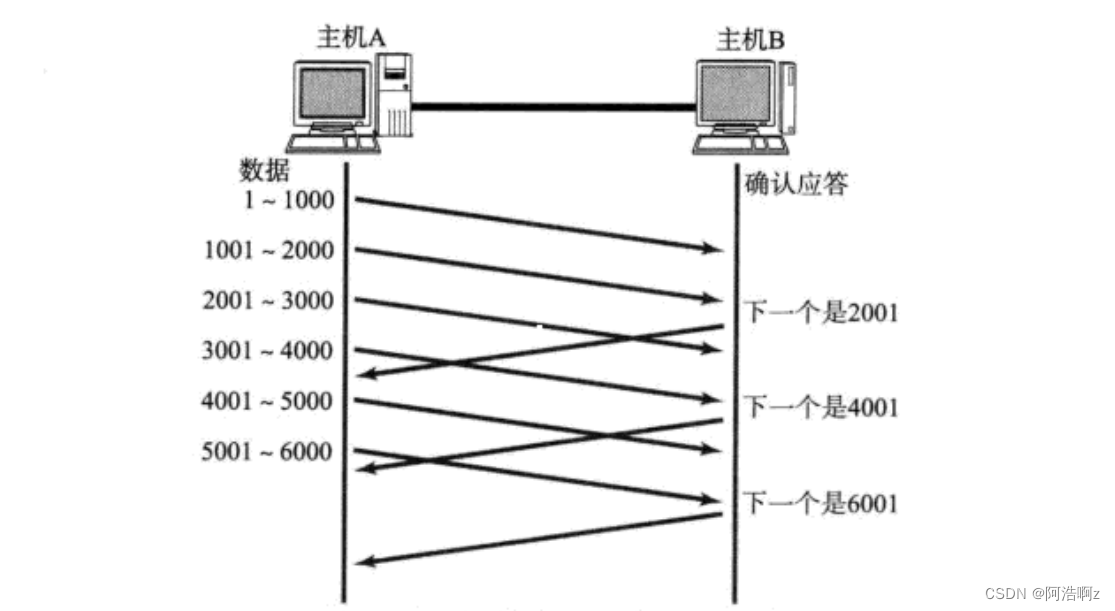
Linux【网络编程】之深入理解TCP协议
Linux【网络编程】之深入理解TCP协议 TCP协议TCP协议段格式4位首部长度---TCP报头长度信息 TCP可靠性(确认应答)&& 提高传输效率确认应答(ACK)机制32位序号与32为确认序号 16位窗口大小---自己接收缓冲区剩余空间的大小16位紧急指针---紧急数据处…...

如何克服看到别人优于自己而感到的焦虑和迷茫?
文章目录 每日一句正能量前言简述自己的感受怎么做如何调整自己的心态后记 每日一句正能量 行动是至于恐惧的良药,而犹豫、拖延,将不断滋养恐惧。 前言 虽然清楚知识需要靠时间沉淀,但在看到自己做不出来的题别人会做,自己写不出的…...
浅谈React中的ref和useRef
目录 什么是useRef? 使用 ref 访问 DOM 元素 Ref和useRef之间的区别 Ref和useRef的使用案例 善用工具 结论 在各种 JavaScript 库和框架中,React 因其开发人员友好性和支持性而得到认可。 大多数开发人员发现 React 非常舒适且可扩展,…...

Linux C 获取主机网卡名及 IP 的几种方法
在进行 Linux 网络编程时,经常会需要获取本机 IP 地址,除了常规的读取配置文件外,本文罗列几种个人所知的编程常用方法,仅供参考,如有错误请指出。 方法一:使用 ioctl() 获取本地 IP 地址 Linux 下可以使用…...

解密外接显卡:笔记本能否接外置显卡?如何连接外接显卡?
伴随着电脑游戏和图形处理的需求不断增加,很多笔记本电脑使用者开始考虑是否能够通过外接显卡来提升性能。然而,外接显卡对于笔记本电脑是否可行,以及如何连接外接显卡,对于很多人来说仍然是一个迷。本文将为您揭秘外接显卡的奥秘…...
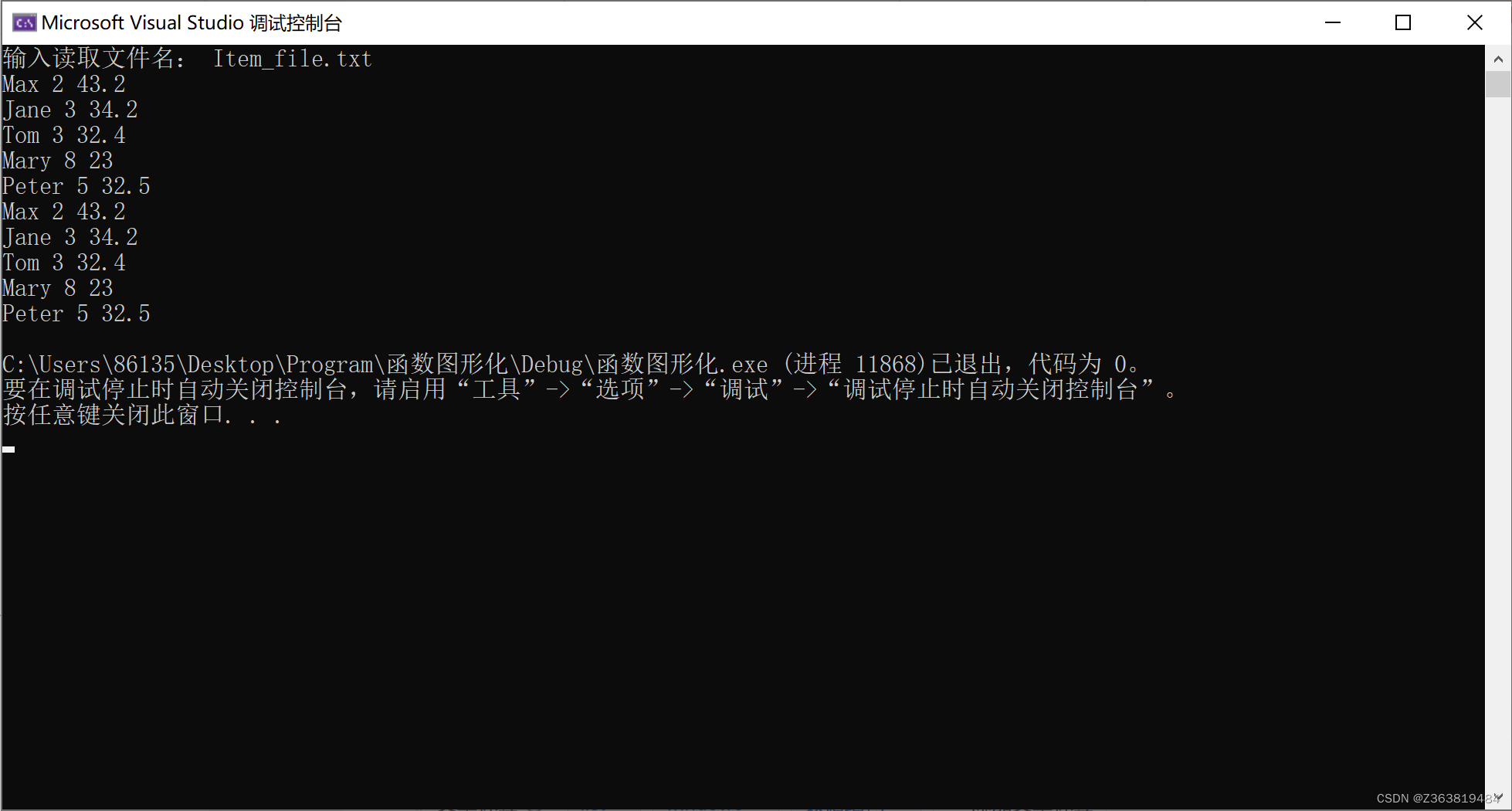
list与erase()
运行代码: //list与erase() #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;Item():name(" "),iid(0),value(0.0){}Item(string ss,int ii,double vv):name(ss),iid(ii),value(vv){}friend istr…...
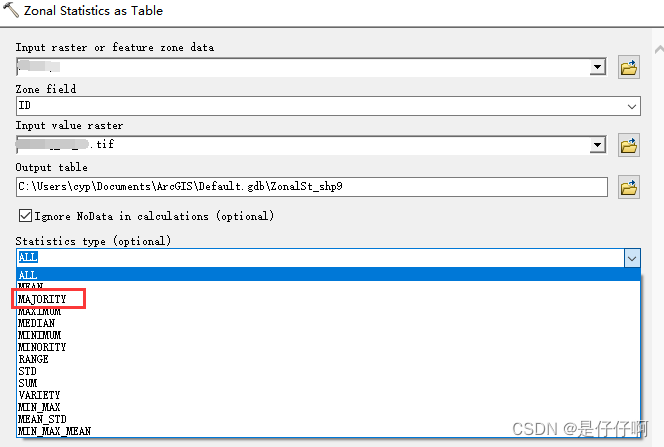
Arcgis 分区统计majority参数统计问题
利用Arcgis 进行分区统计时,需要统计不同矢量区域中栅格数据的众数(majority),出现无法统计majority参数问题解决 解决:利用copy raster工具,将原始栅格数据 64bit转为16bit...
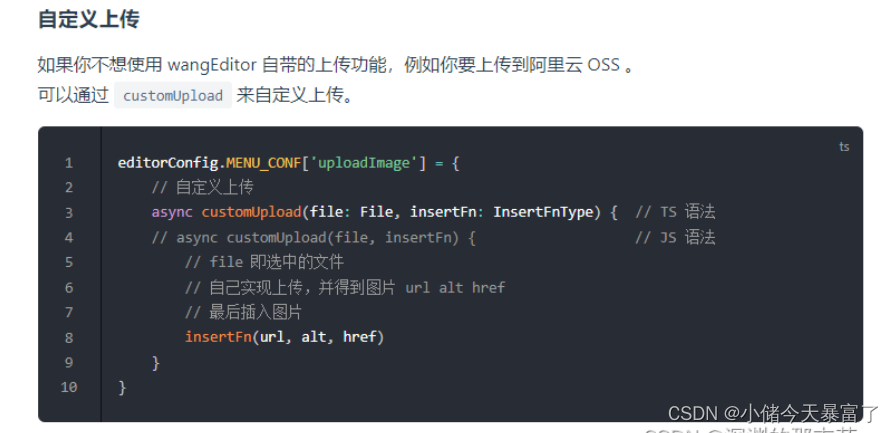
vue2+wangEditor5富文本编辑器(图片视频自定义上传七牛云/服务器)
1、安装使用 安装 yarn add wangeditor/editor # 或者 npm install wangeditor/editor --save yarn add wangeditor/editor-for-vue # 或者 npm install wangeditor/editor-for-vue --save在main.js中引入样式 import wangeditor/editor/dist/css/style.css在使用编辑器的页…...

shell脚本练习--安全封堵脚本,使用firewalld实现
一.什么是安全封堵 安全封堵(security hardening)是指采取一系列措施来增强系统的安全性,防止潜在的攻击和漏洞利用。以下是一些常见的安全封堵措施: 更新和修补系统:定期更新操作系统和软件包以获取最新的安全补丁和修…...

双端冒泡排序
双端冒泡排序是对传统冒泡排序的改进,其主要改进在于同时从两端开始排序,相对于传统冒泡排序每次只从一端开始排序,这样可以减少排序的遍历次数。 传统冒泡排序从一端开始,每次将最大(或最小)的元素冒泡到…...

如何在Visual Studio Code中用Mocha对TypeScript进行测试
目录 使用TypeScript编写测试用例 在Visual Studio Code中使用调试器在线调试代码 首先,本文不是一篇介绍有关TypeScript、JavaScript或其它编程语言数据结构和算法的文章。如果你正在准备一场面试,或者学习某一个课程,互联网上可以找到许多…...

GO中Json的解析
一个json字串,想要拿到其中的数据,就需要解析出来 一、适用于json数据的结构已知的情况下 使用json.Unmarshal将json数据解析到结构体中 根据json字串数据的格式定义struct,用来保存解码后的值。这里首先定义了一个与要解析的数据结构一样的…...

chatgpt 提示词-关于数据科学的 75个词语
这里有 75 个 chatgpt 提示,可以立即将其用于数据科学或数据分析等。 1. 伪装成一个SQL终端 提示:假设您是示例数据库前的 SQL 终端。该数据库包含名为“用户”、“项目”、“订单”、“评级”的表。我将输入查询,您将用终端显示的内容进行…...

(自控原理)控制系统的数学模型
目录 一、时域数学模型 1、线性元件微分方程的建立 2、微分方程的求解方法编辑 3、非线性微分方程的线性化 二、复域数学模型 1、传递函数的定义 2、传递函数的标准形式 3、系统的典型环节的传递函数 4、传递函数的性质 5、控制系统数学模型的建立 6、由传递函数求…...

Webpack5 cacheGroups
文章目录 一、 cacheGroups是什么?二、怎么使用cacheGroups?三、cacheGroups实际应用之一? 一、 cacheGroups是什么? 在Webpack 5中,cacheGroups是用于配置代码拆分的规则,它可以帮助你更细粒度地控制生成…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
