基于回溯算法实现八皇后问题
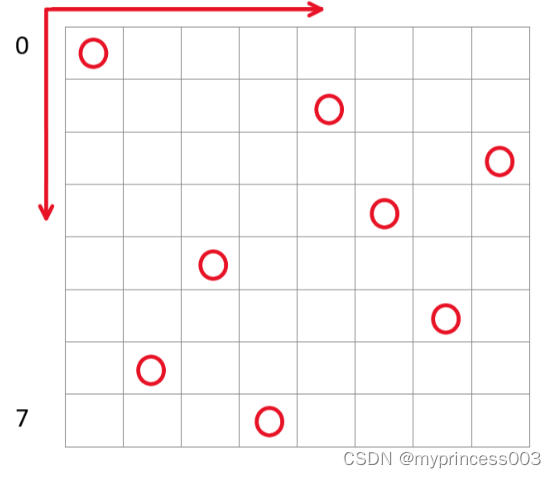
八皇后问题是一个经典的计算机科学问题,它的目标是将8个皇后放置在一个大小为8×8的棋盘上,使得每个皇后都不会攻击到其他的皇后。皇后可以攻击同一行、同一列和同一对角线上的棋子。
一、八皇后问题介绍
八皇后问题最早由国际西洋棋大师马克斯·贝瑟尔在1848年提出,但当时他并不知道如何解决这个问题。后来,在1960年代,计算机科学家们开始研究八皇后问题,并提出了多种解决方法。
二、八皇后问题算法思路分析
解决八皇后问题的算法有很多,其中最常见的是回溯算法。
回溯算法通过尝试所有可能的解来找到正确的解,因此在处理八皇后问题时也可以使用回溯算法来求解。另外,还有其他的一些算法,如位运算和启发式搜索等方法,也可以用来解决八皇后问题。
八皇后问题是一个重要的算法问题,它具有较高的难度和复杂性,同时也有着广泛的应用。在现代的计算机科学领域中,八皇后问题被视为一项基础性的问题,对于提高程序员的算法能力和解决实际问题都有着重要的意义。
八皇后问题算法的核心思路是通过回溯法来找到所有可能的解,并判断是否符合题目要求。
具体地步骤如下:
定义一个棋盘,用二维数组表示,其中0表示空白位置,1表示皇后的位置。
从第一行开始尝试将皇后放置在每一列上,并判断是否和前面的皇后冲突(即同一行、同一列或同一对角线)。
如果当前位置没有冲突,则将皇后放置在该位置,并递归处理下一行。
如果当前位置有冲突,则尝试下一列。
如果无法在当前行中找到合适的位置,则回溯到上一行并尝试其它列。
当处理完所有行时,输出解决方案。
在这个过程中,我们需要定义一些辅助函数来检查某个位置是否可以放置皇后、打印棋盘以及递归函数等。具体实现方式会根据不同的算法思路而有所不同,但以上的基本思路是通用的。
三、八皇后问题的回溯算法代码实现
package com.biyu.demo;public class EightQueens {//有多少个皇后int max = 8;//定义数组array, 保存皇后放置位置的结果int[] array = new int[max];//多少种解法static int count = 0;//冲突次数static int judgeCount = 0;public static void main(String[] args) {EightQueens queue8= new EightQueens();queue8.check(0);System.out.printf("一共有%d解法", count);System.out.printf("一共判断冲突的次数%d次", judgeCount);}/*** 放置第n个皇后** @param n*/private void check(int n) {if (n == max) {printBoard();return;}//依次放入皇后,并判断是否冲突for (int i = 0; i < max; i++) {//先把当前这个皇后 n , 放到该行的第1列array[n] = i;//判断当放置第n个皇后到i列时,是否冲突if (judge(n)) { // 不冲突//接着放n+1个皇后,即开始递归check(n + 1); //}}}/*** 检测该皇后是否和前面已经摆放的皇后冲突** @param n 表示第n个皇后* @return*/private boolean judge(int n) {judgeCount++;for (int i = 0; i < n; i++) {//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线// n = 1 放置第 2列 1 n = 1 array[1] = 1// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1//3. 判断是否在同一行, 没有必要,n 每次都在递增if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {return false;}}return true;}/*** 输出皇后摆放的位置*/private void printBoard() {count++;for (int i = 0; i < array.length; i++) {System.out.print(array[i] + " ");}System.out.println();}}
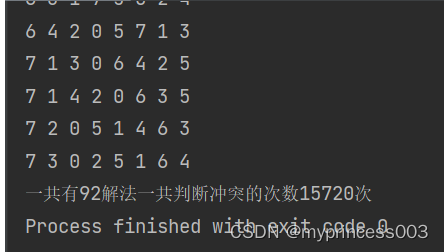
八皇后问题的解不止一个,因此我们需要找到所有的解才能得到正确的结果。同时,在实现算法时应该尽量避免重复计算,以提高效率。
相关文章:

基于回溯算法实现八皇后问题
八皇后问题是一个经典的计算机科学问题,它的目标是将8个皇后放置在一个大小为88的棋盘上,使得每个皇后都不会攻击到其他的皇后。皇后可以攻击同一行、同一列和同一对角线上的棋子。 一、八皇后问题介绍 八皇后问题最早由国际西洋棋大师马克斯贝瑟尔在18…...
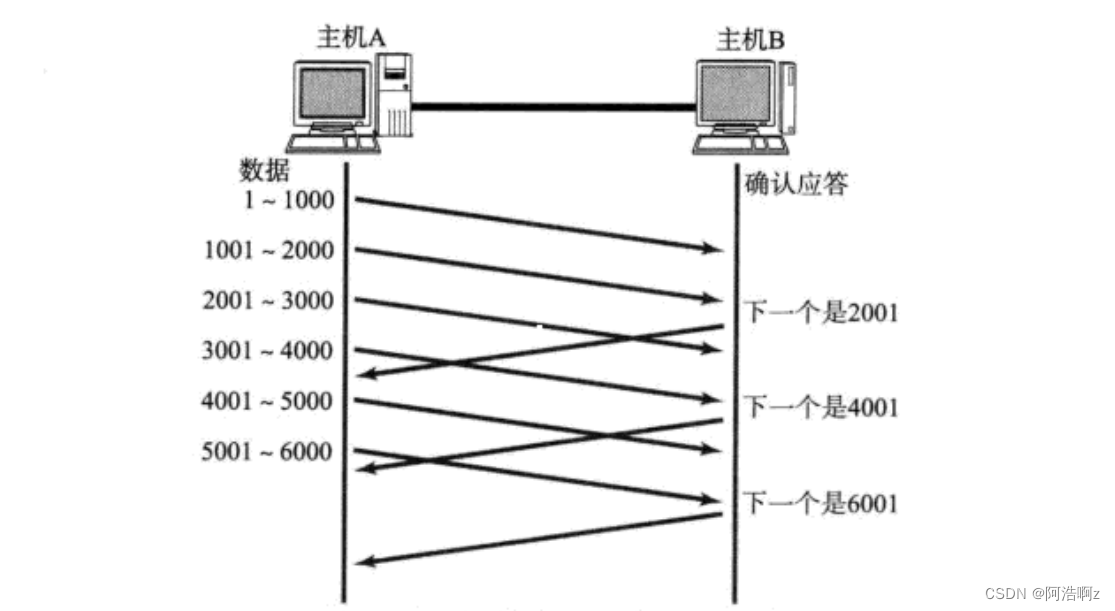
Linux【网络编程】之深入理解TCP协议
Linux【网络编程】之深入理解TCP协议 TCP协议TCP协议段格式4位首部长度---TCP报头长度信息 TCP可靠性(确认应答)&& 提高传输效率确认应答(ACK)机制32位序号与32为确认序号 16位窗口大小---自己接收缓冲区剩余空间的大小16位紧急指针---紧急数据处…...

如何克服看到别人优于自己而感到的焦虑和迷茫?
文章目录 每日一句正能量前言简述自己的感受怎么做如何调整自己的心态后记 每日一句正能量 行动是至于恐惧的良药,而犹豫、拖延,将不断滋养恐惧。 前言 虽然清楚知识需要靠时间沉淀,但在看到自己做不出来的题别人会做,自己写不出的…...
浅谈React中的ref和useRef
目录 什么是useRef? 使用 ref 访问 DOM 元素 Ref和useRef之间的区别 Ref和useRef的使用案例 善用工具 结论 在各种 JavaScript 库和框架中,React 因其开发人员友好性和支持性而得到认可。 大多数开发人员发现 React 非常舒适且可扩展,…...

Linux C 获取主机网卡名及 IP 的几种方法
在进行 Linux 网络编程时,经常会需要获取本机 IP 地址,除了常规的读取配置文件外,本文罗列几种个人所知的编程常用方法,仅供参考,如有错误请指出。 方法一:使用 ioctl() 获取本地 IP 地址 Linux 下可以使用…...

解密外接显卡:笔记本能否接外置显卡?如何连接外接显卡?
伴随着电脑游戏和图形处理的需求不断增加,很多笔记本电脑使用者开始考虑是否能够通过外接显卡来提升性能。然而,外接显卡对于笔记本电脑是否可行,以及如何连接外接显卡,对于很多人来说仍然是一个迷。本文将为您揭秘外接显卡的奥秘…...
list与erase()
运行代码: //list与erase() #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;Item():name(" "),iid(0),value(0.0){}Item(string ss,int ii,double vv):name(ss),iid(ii),value(vv){}friend istr…...
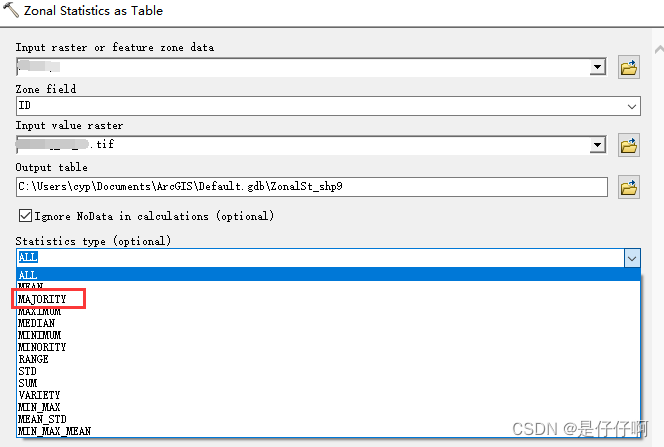
Arcgis 分区统计majority参数统计问题
利用Arcgis 进行分区统计时,需要统计不同矢量区域中栅格数据的众数(majority),出现无法统计majority参数问题解决 解决:利用copy raster工具,将原始栅格数据 64bit转为16bit...
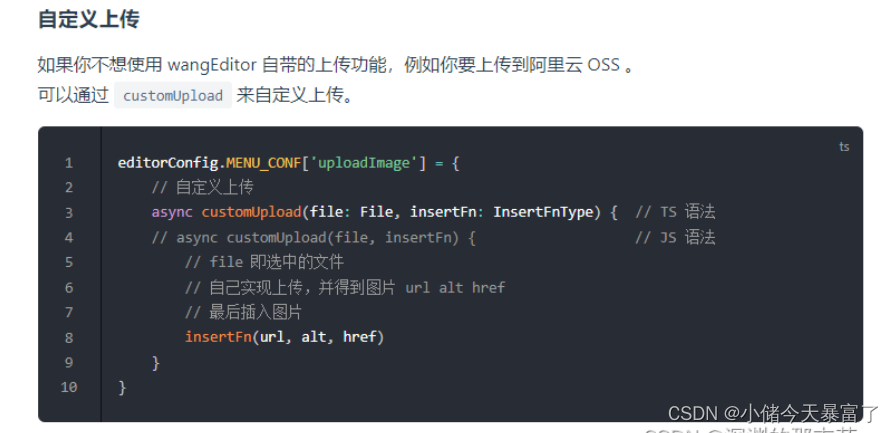
vue2+wangEditor5富文本编辑器(图片视频自定义上传七牛云/服务器)
1、安装使用 安装 yarn add wangeditor/editor # 或者 npm install wangeditor/editor --save yarn add wangeditor/editor-for-vue # 或者 npm install wangeditor/editor-for-vue --save在main.js中引入样式 import wangeditor/editor/dist/css/style.css在使用编辑器的页…...

shell脚本练习--安全封堵脚本,使用firewalld实现
一.什么是安全封堵 安全封堵(security hardening)是指采取一系列措施来增强系统的安全性,防止潜在的攻击和漏洞利用。以下是一些常见的安全封堵措施: 更新和修补系统:定期更新操作系统和软件包以获取最新的安全补丁和修…...

双端冒泡排序
双端冒泡排序是对传统冒泡排序的改进,其主要改进在于同时从两端开始排序,相对于传统冒泡排序每次只从一端开始排序,这样可以减少排序的遍历次数。 传统冒泡排序从一端开始,每次将最大(或最小)的元素冒泡到…...

如何在Visual Studio Code中用Mocha对TypeScript进行测试
目录 使用TypeScript编写测试用例 在Visual Studio Code中使用调试器在线调试代码 首先,本文不是一篇介绍有关TypeScript、JavaScript或其它编程语言数据结构和算法的文章。如果你正在准备一场面试,或者学习某一个课程,互联网上可以找到许多…...

GO中Json的解析
一个json字串,想要拿到其中的数据,就需要解析出来 一、适用于json数据的结构已知的情况下 使用json.Unmarshal将json数据解析到结构体中 根据json字串数据的格式定义struct,用来保存解码后的值。这里首先定义了一个与要解析的数据结构一样的…...

chatgpt 提示词-关于数据科学的 75个词语
这里有 75 个 chatgpt 提示,可以立即将其用于数据科学或数据分析等。 1. 伪装成一个SQL终端 提示:假设您是示例数据库前的 SQL 终端。该数据库包含名为“用户”、“项目”、“订单”、“评级”的表。我将输入查询,您将用终端显示的内容进行…...

(自控原理)控制系统的数学模型
目录 一、时域数学模型 1、线性元件微分方程的建立 2、微分方程的求解方法编辑 3、非线性微分方程的线性化 二、复域数学模型 1、传递函数的定义 2、传递函数的标准形式 3、系统的典型环节的传递函数 4、传递函数的性质 5、控制系统数学模型的建立 6、由传递函数求…...

Webpack5 cacheGroups
文章目录 一、 cacheGroups是什么?二、怎么使用cacheGroups?三、cacheGroups实际应用之一? 一、 cacheGroups是什么? 在Webpack 5中,cacheGroups是用于配置代码拆分的规则,它可以帮助你更细粒度地控制生成…...
每篇10题)
前端面试的游览器部分(5)每篇10题
41.什么是浏览器的同步和异步加载脚本的区别?你更倾向于使用哪种方式,并解释原因。 浏览器的同步和异步加载脚本是两种不同的脚本加载方式,它们的主要区别在于加载脚本时是否阻塞页面的解析和渲染。 同步加载脚本: 同步加载脚本…...

数据挖掘七种常用的方法汇总
数据挖掘(Data Mining)就是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中,提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。这个定义包括几层含义:数据源必须是真实的、大量的、含噪声的;发现的是用户…...
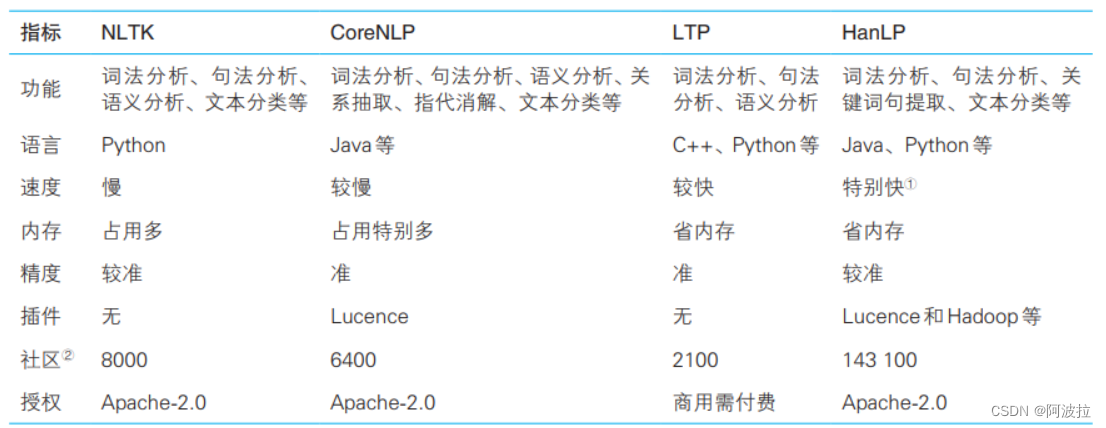
自然语言处理学习笔记(二)————语料库与开源工具
目录 1.语料库 2.语料库建设 (1)规范制定 (2)人员培训 (3)人工标注 3.中文处理中的常见语料库 (1)中文分词语料库 (2)词性标注语料库 (3…...

Rust dyn - 动态分发 trait 对象
dyn - 动态分发 trait 对象 dyn是关键字,用于指示一个类型是动态分发(dynamic dispatch),也就是说,它是通过trait object实现的。这意味着这个类型在编译期间不确定,只有在运行时才能确定。 practice tr…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
