ESD防静电监控系统在SMT产线中的应用案例
作为电子厂的关键制造环节之一,SMT(表面贴装技术)产线的效率和质量对企业的竞争力至关重要。为了提高生产线的管理效率和保障生产环境的质量,许多电子厂开始采用MES生产管理系统和ESD防静电监控系统的综合解决方案。

在SMT产线中安装一套MES生产管理系统可以实现对产线的全面监控和管理。该系统可以统计每条产线每天白班和夜班的产量,完成率,设备运行状况等关键指标,并汇总近半年的生产状况,以便企业管理层做出及时的决策。通过这种方式,生产线的生产效率可以得到有效的提高,同时也可以准确评估设备的运行状态,及时发现和解决潜在问题。
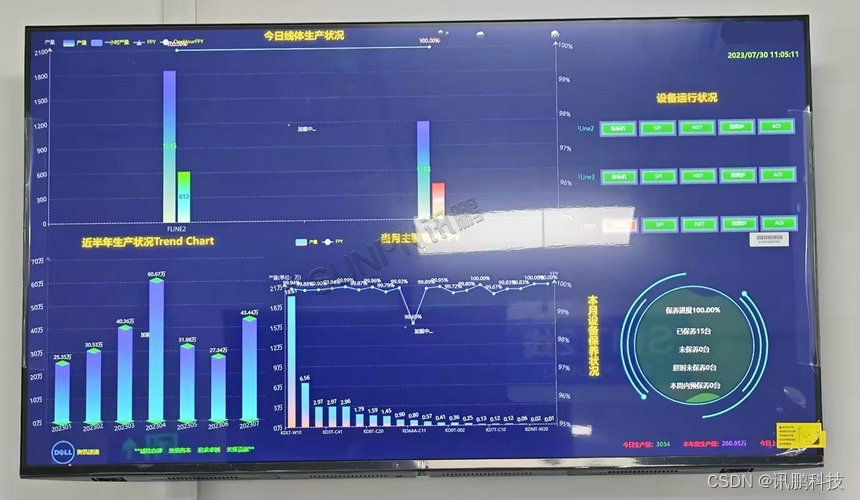
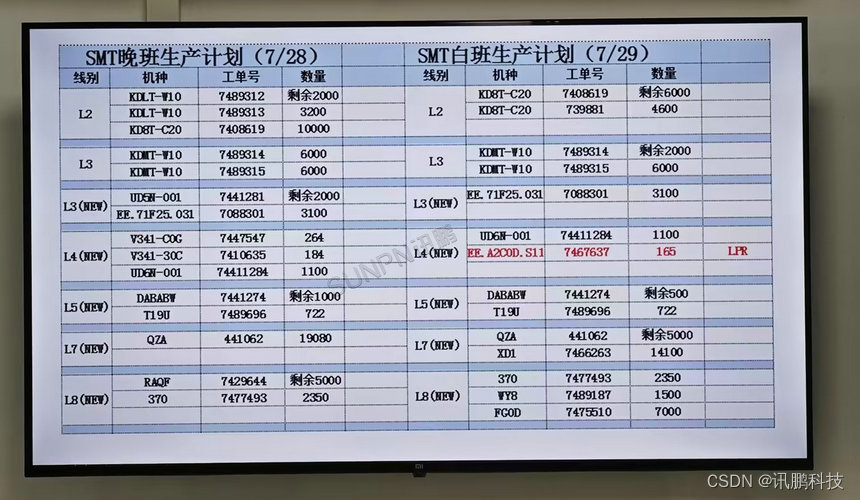
为了解决长期以来在静电监控和数据采集记录方面存在的困难,电子厂还可以集成ESD防静电监控系统。ESD防静电监控系统是一种数字化管理工具,可以对企业的防静电设备(包括机器、台垫、离子风机)和人员进行实时监控、数据储存和动态显示。

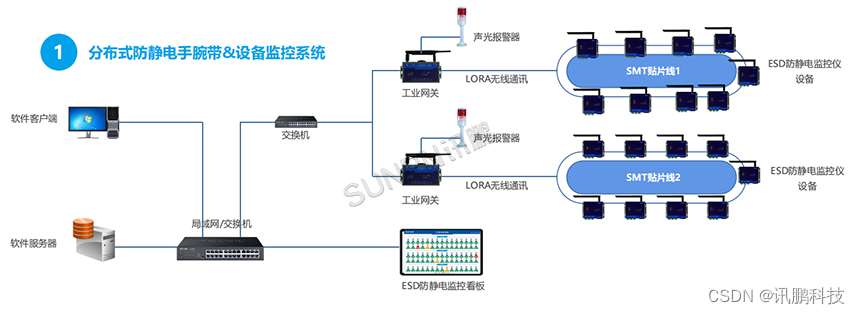
这套系统由管理软件、现场显示屏和讯鹏自主研发的防静电监控仪组成。防静电监控仪可以通过对防静电手腕带和生产设备的实时监测,将数据传输给管理软件进行存储,并实时发送至现场显示屏。通过这种方式,现场的管理人员可以时刻精准了解生产现场的静电防护情况。

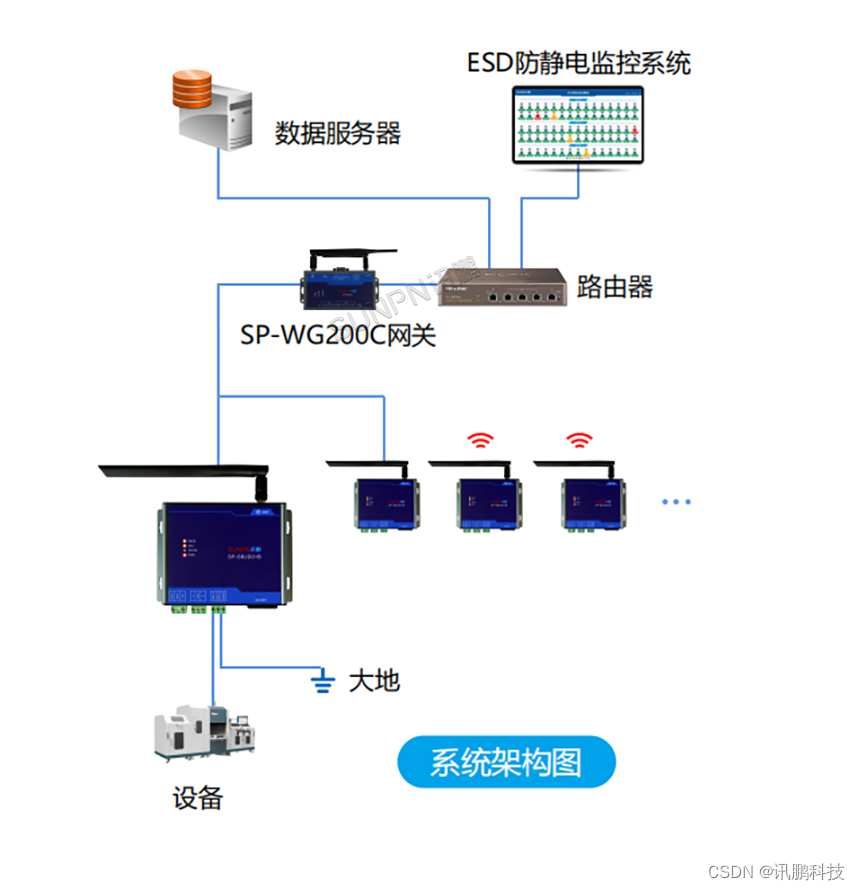
集成ESD防静电监控系统对电子厂来说具有诸多优势。首先,通过实时监控防静电设备和人员,可以确保防静电措施的有效实施,减少静电的产生和累积,为电子产品的生产提供更可靠的保障。其次,数据的实时储存和显示,使管理人员可以随时查看生产现场的静电防护情况,及时采取措施纠正问题。最重要的是,ESD防静电监控系统可以为公司提供宝贵的数据,为持续改进和优化生产流程提供决策支持。

通过在SMT产线中安装MES生产管理系统和集成ESD防静电监控系统,电子厂可以实现对生产线的全面监控和管理,提高生产效率,确保生产质量。这些技术的应用为企业创造了更为稳定和安全的生产环境,提升了企业的竞争力和可持续发展能力。未来,随着科技的不断进步,我们有理由相信这些技术将会进一步完善和创新,为电子产业带来更多的发展机遇。
【X】
相关文章:

ESD防静电监控系统在SMT产线中的应用案例
作为电子厂的关键制造环节之一,SMT(表面贴装技术)产线的效率和质量对企业的竞争力至关重要。为了提高生产线的管理效率和保障生产环境的质量,许多电子厂开始采用MES生产管理系统和ESD防静电监控系统的综合解决方案。 在SMT产线中安…...

Vue+Nodejs+Express+Minio 实现本地图片上传
安装Minio,Minio server和Minio client都要下载可以自定义安装目录 安装完成之后,可以将minio配置成环境变量方便使用 配置了环境变量启动命令式 minio server start,默认账号密码minioadmin和minioadmin,点击9000端口的这个链接,即可访问客户端 nodejs连接Minio,简易服务进…...
em3288 linux_4.19 第一次烧写无法进入内核的情况
1. 情况一: /DDR Version 1.11 20210818 In SRX Channel a: DDR3 400MHz Bus Width32 Col10 Bank8 Row15 CS1 Die Bus-Width16 Size1024MB Channel b: DDR3 400MHz Bus Width32 Col10 Bank8 Row15 CS1 Die Bus-Width16 Size1024MB OUT Boot1 Release Time: Jul 22 2…...

【Java多线程学习5】什么是悲观锁,什么是乐观锁?如何实现乐观锁、乐观锁存在哪些问题
【Java多线程学习5】什么是悲观锁,什么是乐观锁?如何实现乐观锁、乐观锁存在哪些问题 一、什么是悲观锁 概述 悲观锁总是假设最坏的情况,认为共享资源每次被访问的时候就会出现问题(比如共享数据被修改),所以每次在获取资源操作…...
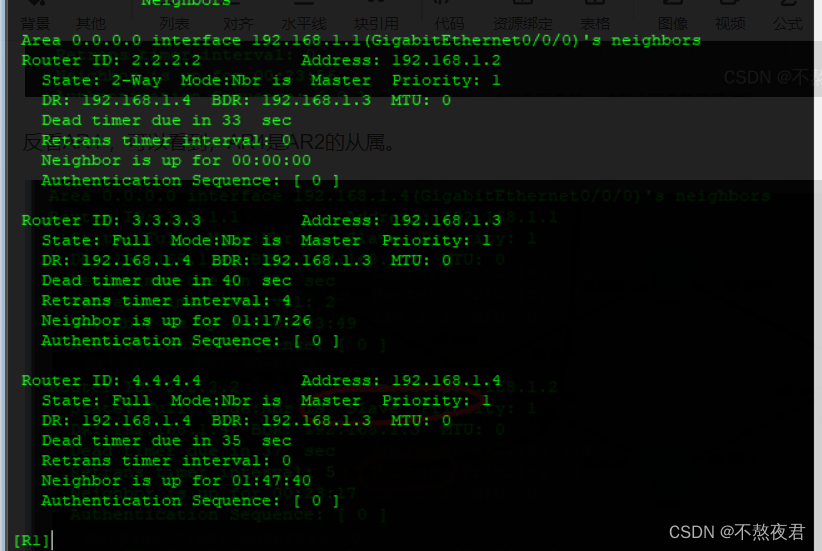
OSPF协议RIP协议+OSPF实验(eNSP)
本篇博客主要讲解单区域的ospf,多区域的仅作了解。 目录 一、OSPF路由协议概述 1.内部网关协议和外部网关协议 二、OSPF的应用环境 1.从以下几方面考虑OSPF的使用 2.OSPF的特点 三、OSPF重要基本概念 3.1,辨析邻居和邻接关系以及七种邻居状态 3…...
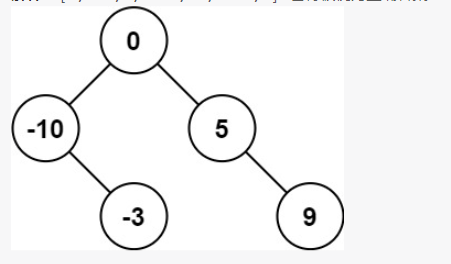
leetcode每日一练-第108题-将有序数组转换为二叉搜索树
一、思路 递归 二、解题方法 在给定中序遍历序列数组的情况下,每一个子树中的数字在数组中一定是连续的,因此可以通过数组下标范围确定子树包含的数字,下标范围记为 [left,right]。对于整个中序遍历序列,下标范围从 left0到 ri…...
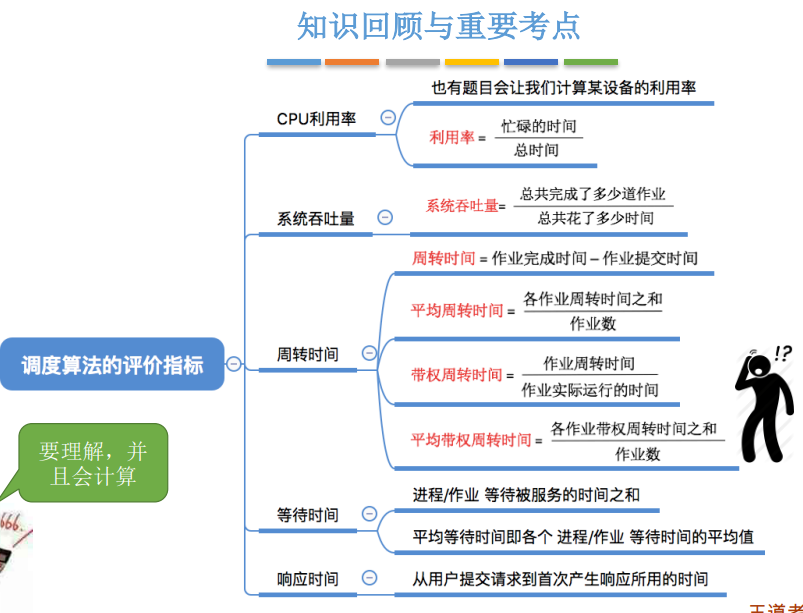
王道《操作系统》学习(二)—— 进程管理(二)
2.1 处理机调度的概念、层次 2.1.1 调度的基本概念 2.1.2 调度的三个层次 (1)高级调度(作业调度) (2)中级调度(内存调度) 补充知识:进程的挂起状态和七状态模型 &#x…...
Vulnhub: shenron: 3靶机
kali:192.168.111.111 靶机:192.168.111.171 信息收集 端口扫描 nmap -A -sC -v -sV -T5 -p- --scripthttp-enum 192.168.111.171 修改hosts后访问目标80端口,发现是wordpress wpscan收集目标用户,爆破出密码:ilov…...
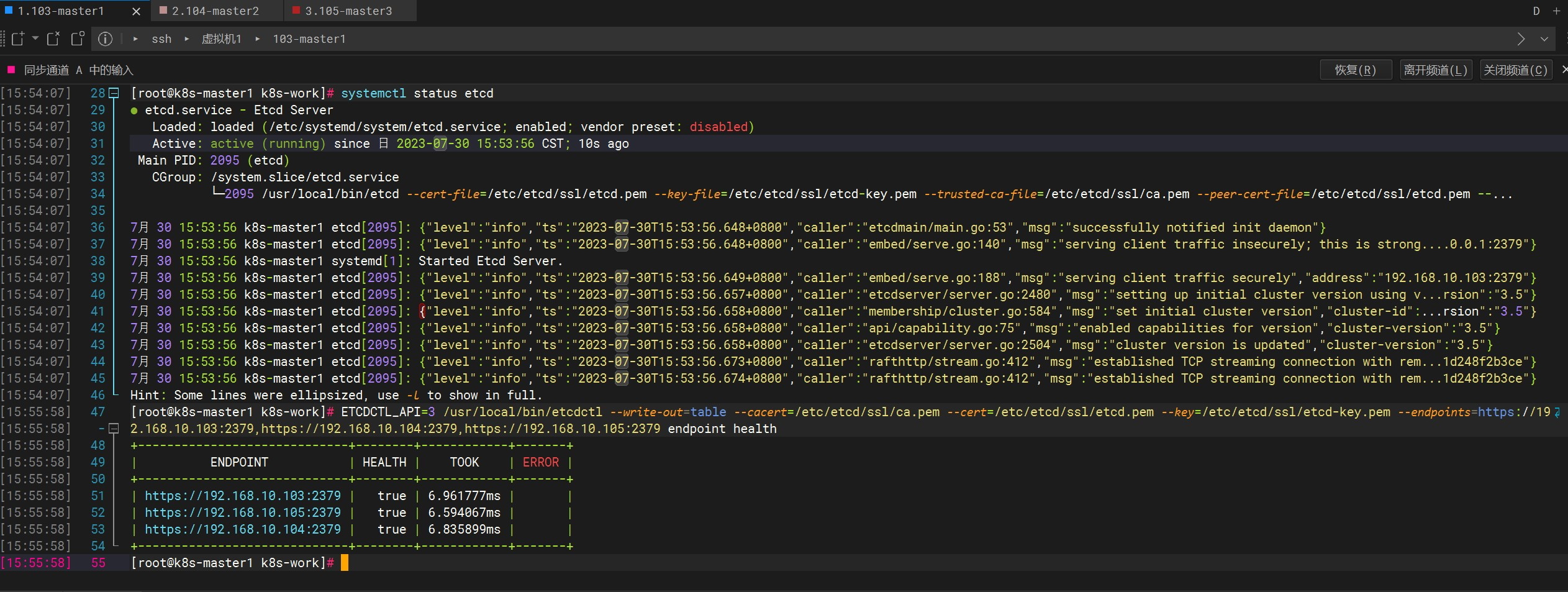
Kubernetes高可用集群二进制部署(二)ETCD集群部署
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...

mysql主从复制及原理
目录 主从复制原理实现主从复制 主从复制原理 主要基于MySQL二进制日志 主要包括三个线程(2个I/O线程,1个SQL线程) 1、MySQL将数据变化记录到二进制日志中; 2、Slave将MySQL的二进制日志拷贝到Slave的中继日志中; …...

MQTT服务器详细介绍:连接物联网的通信枢纽
随着物联网技术的不断发展,MQTT(Message Queuing Telemetry Transport)协议作为一种轻量级、可靠、灵活的通信协议,被广泛应用于物联网领域。在MQTT系统中,MQTT服务器扮演着重要的角色,作为连接物联网设备和…...

通过VBA宏合并Excel工作表
工作中经常会用到的把几个Excel文件合并到一个,或者是把一个Excel文件里的所有Sheet合并到一个Sheet来进行统计。下面分别提供用vba宏来解决这两个问题的方法。 1、合并Excel文件 打开一个空Excel文件,AltF11,插入一个模块,开始…...
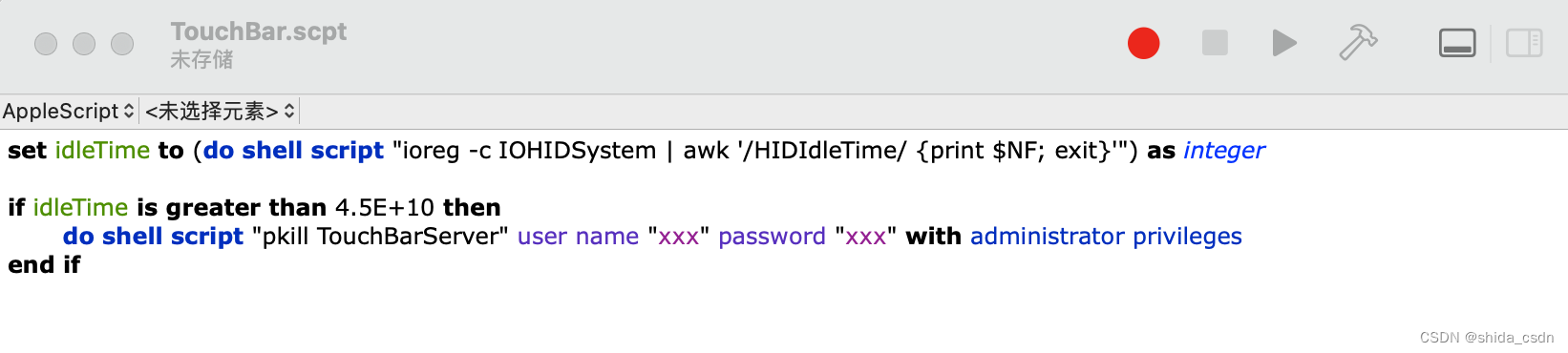
Mac 定时重启 TouchBar 脚本(缓解闪烁问题)
背景 Mac 笔记本 TouchBar 是真的脆啊,合盖使用一段时间就废了,右侧一直闪烁简直亮瞎眼 😂 经过观察,总结出闪烁规律如下: 工作状态:不断操作电脑时,触控栏处于工作状态,几乎不闪…...

Redis主从复制、哨兵机制、集群分片
目录 一.主从复制 1.概述 2.主从架构相比于单点架构的优势 3.主从复制原理和工作流程 第一次同步 第一阶段:建立链接、协商同步 第二阶段:主服务器同步数据给从服务器 第三阶段:主服务器发送新写操作命令给从服务器 基于长连接的命…...
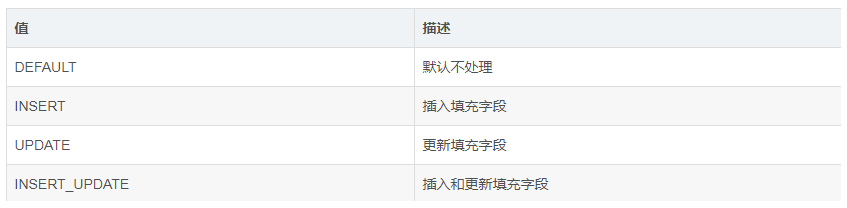
字段填充策略 FieldFill
实体类中有如下属性,通过上面的自动填充属性,我们可以实现在进行插入(insert)操作时对添加了注解TableField(fill FieldFill.INSERT)的字段进行自动填充(解释:后面会写配置自动填充的配置类,该…...

Docker run 启动容器报错
今天在Windows下启动docker容器发现的三个错误: Ports are not available: exposing port TCP 0.0.0.0:1521 -> 0.0.0.0:0: listen tcp 0.0.0.0:1521: bind: Only one usage of each socket address (protocol/network address/port) is normally permitted. 端口…...

Golang之路---03 面向对象——类型断言
类型断言 作用 检查 i 是否为 nil检查 i 存储的值是否为某个类型 使用方式 第一种: t : i.(T)这个表达式可以断言一个接口对象(i)里不是 nil,并且接口对象(i)存储的值的类型是 T,如果断言成…...
Atcoder 做题记录
My OI Blog A R C 155 F \mathbb{ARC \ 155 \ F} ARC 155 F E, F 先咕着,做一些多项式题,这篇题解是我人工翻译的 [1] Double Counting 双重计数 考虑从叶子节点开始,用唯一的方式(如果有的话)来构造出一棵满足条件的树…...
C++之观察者模式(发布-订阅)
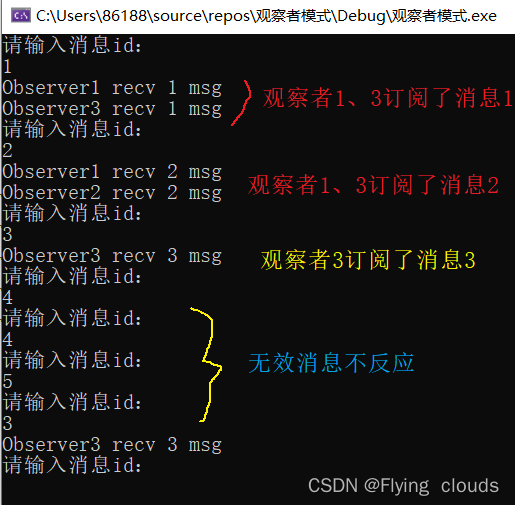
目录 模式简介 介绍 优点 缺点 代码实现 场景说明 实现代码 运行结果 模式简介 观察者模式(Observer Pattern),也叫我们熟知的发布-订阅模式。 它是一种行为型模式。 介绍 观察者模式主要关注的是对象的一对多的关系, …...

无头单链表,有完整测试程序
🍟无头单链表 👻无头单链表的所有结点都存储有效信息 👻无头单链表相对带头单链表,在有些涉及更改头节点的函数上需要传二级指针 🍟头文件list.h #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #includ…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
