2023年第四届“华数杯”数学建模思路 - 案例:最短时间生产计划安排
文章目录
- 0 赛题思路
- 1 模型描述
- 2 实例
- 2.1 问题描述
- 2.2 数学模型
- 2.2.1 模型流程
- 2.2.2 符号约定
- 2.2.3 求解模型
- 2.3 相关代码
- 2.4 模型求解结果
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
最短时间生产计划模型
该模型出现在好几个竞赛赛题上,预测2022今年国赛也会与该模型相关。
1 模型描述
离散系统仿真在工业生产的工序安排中起到了相当重要的作用,如何就一些内部机制复杂的离散问题建立简单易行、可监测性强的数学模型一直是仿真技术的研究热点.
离散事件系统现有三种仿真建模策略,即:
- 事件调度法
- 活动扫描法
- 进程交互法.
该模型demo学长采用了其中的活动扫描法对生产中的一个实际例子进行了处理.
活动扫描法对于各事件之间相关性很强的系统有着很好的适用性.
2 实例
2.1 问题描述
在许多工厂生产过程中,由于设备的数量、产品加工的次序限制,往往不能简单地安排生产任务.我们设想,应用强大的数学软件配合简单易行的方法进行安排.
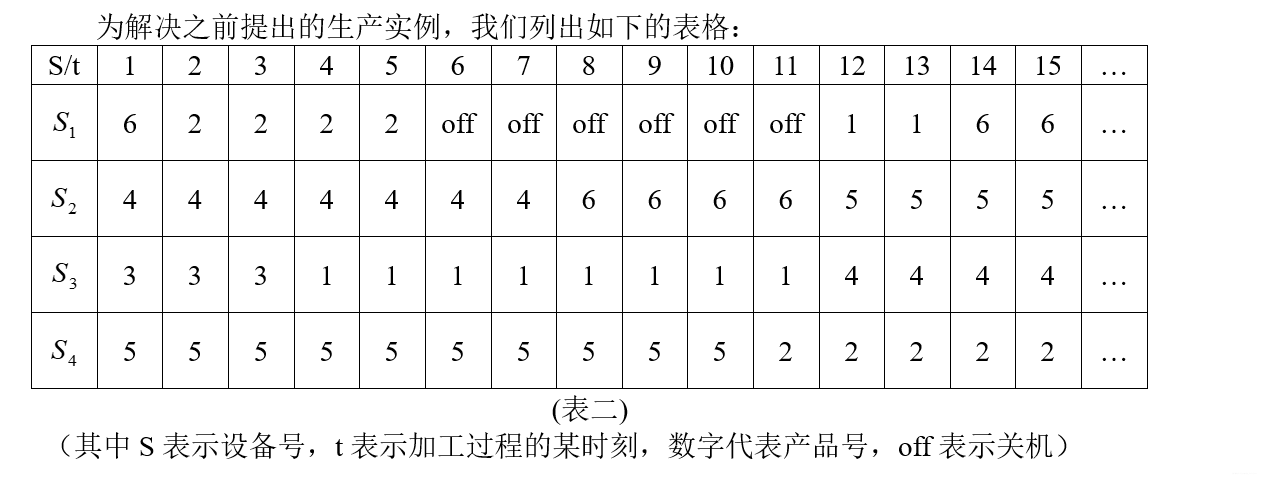
设某重型机械厂产品都是单件性的,其中有一车间共有4种不同设备,现接受6件产品的加工任务,每件产品接受的程序在指定的设备上加工,其工序与加工周期如下表

现在我们根据这一实际问题,寻求安排的方法.
要求:
1、每件产品必须按规定的工序加工,不得颠倒.
2、每台设备在同一时间只能担任一项任务(每件产品的每个工序为一个任务).
3、在尽可能短的时间里,完成所接受的全部任务.
为了节省电能,合理分配生产任务,厂方还要求:
1、做出每件产品的每个工序开工、完工时间表.
2、给出每台设备承担任务的时间表.
2.2 数学模型
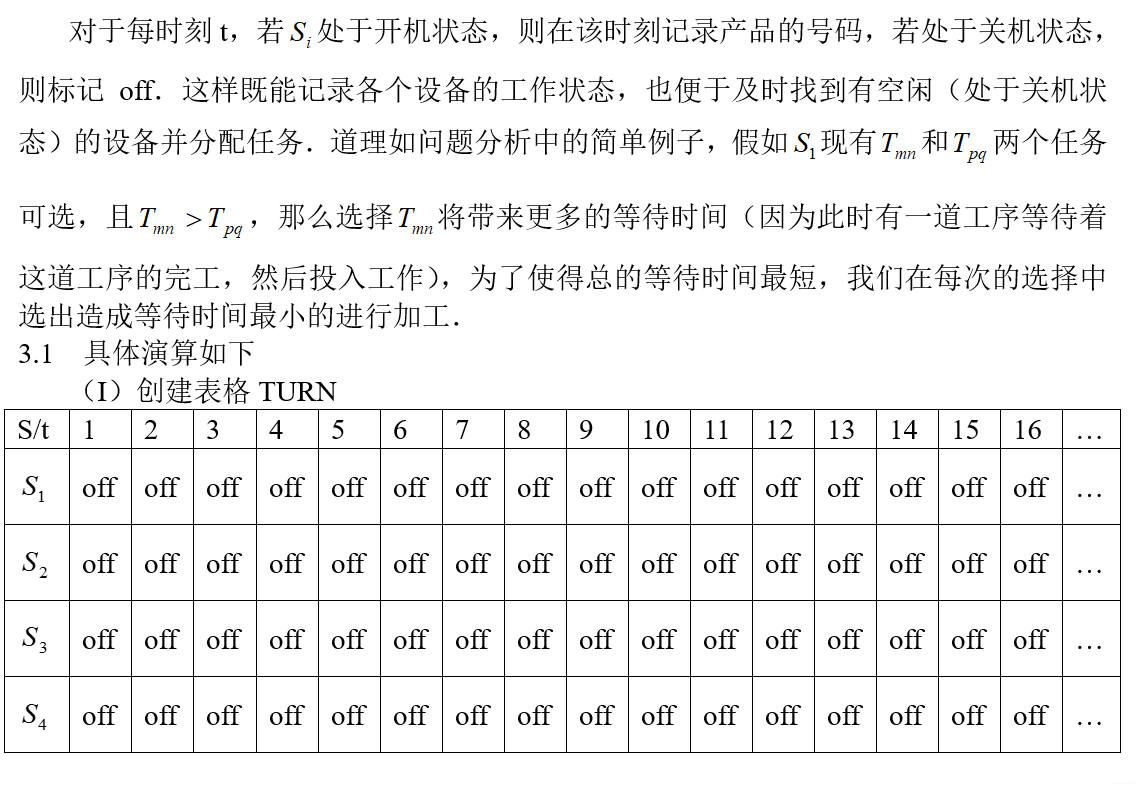
2.2.1 模型流程

2.2.2 符号约定

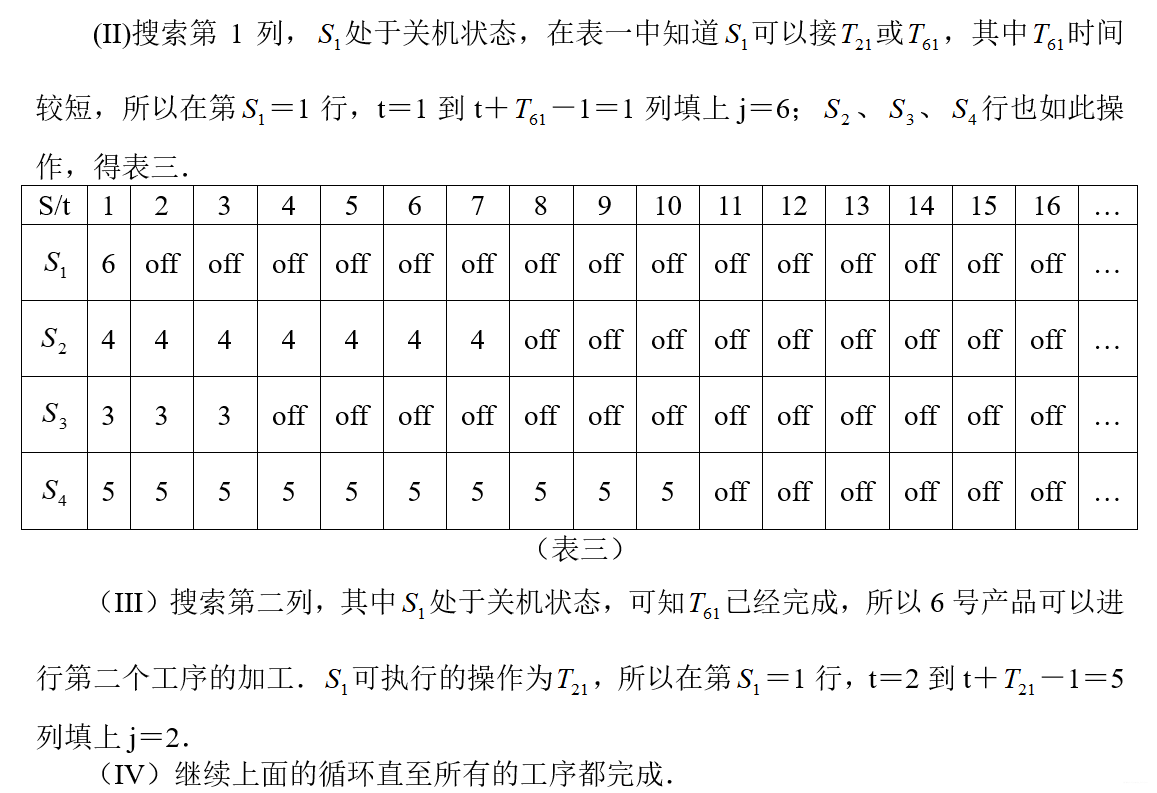
2.2.3 求解模型
2.3 相关代码
clear
clc
seq=[3 1 2 3 4 0 0 0 %各产品加工时所用的设备的次序1 4 2 3 0 0 0 03 4 1 2 1 0 0 02 3 4 1 4 3 0 04 2 3 4 1 3 4 01 2 1 3 4 1 3 1];tim=[8 2 4 24 6 0 0 0 %加工对应使用的时间4 5 3 4 0 0 0 03 7 15 20 8 0 0 07 6 21 1 16 3 0 010 4 8 4 12 6 1 01 4 7 3 5 2 5 8];
whole=[0 0 0 0];
for i=1:6for j=1:8if(seq(i,j)~=0)whole(seq(i,j))=whole(seq(i,j))+tim(i,j);endend
end
whole %生产各件产品所需的总时间mes=cell(4,1); %记录各个设备的工作时间(对应于上面tim的位置)
for k=1:4mes{k,1}=zeros(6,8);for j=1:8for i=1:6if(seq(i,j)==k)mes{k,1}(i,j)=tim(i,j);elsemes{k,1}(i,j)=100;endendend
endturn=cell(5,100); %记录四个设备的开关时间及加工对象(on(i))
for i=1:4for j=1:100turn{i,j}='off';end
end
for i=1:100turn{5,i}=[num2str(i) '分'];
endopen=zeros(6,8);
%记录6个产品的加工进度,0表示未进行,1表示已开始(或已结束),2表示可选,3表示没有这个程序
for i=1:6open(i,1)=2;
end
for i=1:6for j=1:8if seq(i,j)==0open(i,j)=3;endend
endgongxu=zeros(6,1);
dai=zeros(4,1);
j=1;
s=[1 1 1 1 1 3 3 3
1 1 1 1 3 3 3 3
1 1 1 1 1 3 3 3
1 1 1 1 1 1 3 3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1];
while isequal(open,s)==0on=[];for i=1:4if turn{i,j}=='off'
%在turn矩阵中逐列搜索,若设备处于关机状态,则作记录(可用)on=[on i];endendl1=length(on);for m=1:l1 %在整个生产计划中(对设备逐个)寻找能够选作操作的步骤[x,y]=find(open==2);l2=length(x);a=[x(1) y(1)];for k=1:l2 %对某个设备on(m),找出当前它能操作的步骤中耗时最小的一个if mes{on(m)}(a(1),a(2))>mes{on(m)}(x(k),y(k))a=[x(k) y(k)];endendif turn{on(m),j}=='off' & mes{on(m)}(a(1),a(2))~=100
%若时间为100则意味着这个步骤不属于我们希望使用的那件设备while tim(a(1),a(2))>0turn{on(m),tim(a(1),a(2))+j-1}=a(1);tim(a(1),a(2))=tim(a(1),a(2))-1;endendendfor i=1:4if turn{i,j}~='off'dai(i)=turn{i,j};endendfor i=1:4if turn{i,j}~='off' & turn{i,j+1}=='off'gongxu(turn{i,j})=gongxu(turn{i,j})+1;open(turn{i,j},gongxu(turn{i,j}))=1;endif gongxu(dai(i))<8 & open(dai(i),gongxu(dai(i))+1)~=3 & turn{i,j+1}=='off'open(dai(i),gongxu(dai(i))+1)=2;endendj=j+1;
end2.4 模型求解结果
每件产品的每个工序开工、完工时间表

每台设备承担任务的时间表
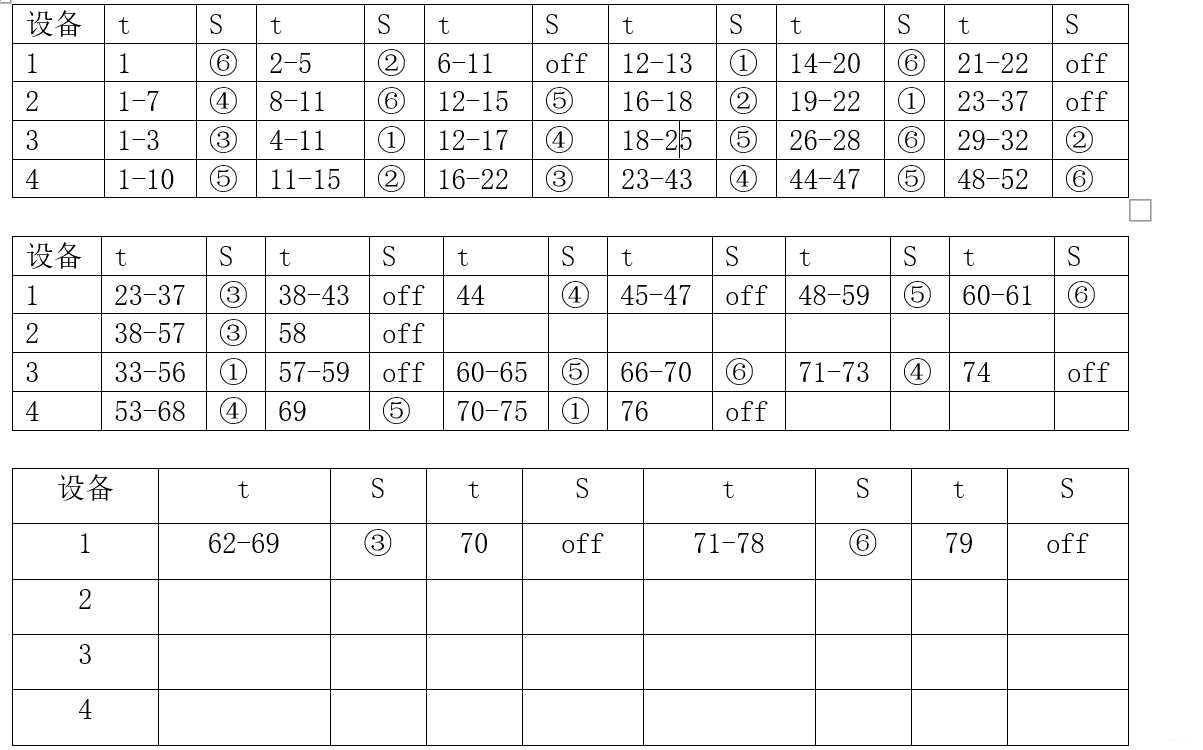
从结果中我们可以看到,使用这种方法,只需78个单位时间就可以完成所有的工序.而我们同时也可以在论文的开始部分看到,单就完成 就需耗费75个单位时间.可见这种方法得出的结果还是相当使人满意的,而且操作简单,可监测性强.
相关文章:

2023年第四届“华数杯”数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 0 赛题思路 (赛题出来以后第一时间在CSDN分享) 最短时间生产计划模型 该模型出现在好几个竞赛赛题上&#x…...

LeetCode404. 左叶子之和
404. 左叶子之和 文章目录 [404. 左叶子之和](https://leetcode.cn/problems/sum-of-left-leaves/)一、题目二、题解方法一:递归方法二:迭代 一、题目 给定二叉树的根节点 root ,返回所有左叶子之和。 示例 1: 输入: root [3,9…...
Nginx 高性能内存池 ----【学习笔记】
跟着这篇文章学习: c代码实现一个高性能内存池(超详细版本)_c 内存池库_linux大本营的博客-CSDN博客https://blog.csdn.net/qq_40989769/article/details/130874660以及这个视频学习: nginx的内存池_哔哩哔哩_bilibilihttps://w…...
iOS--frame和bounds
坐标系 首先,我们来看一下iOS特有的坐标系,在iOS坐标系中以左上角为坐标原点,往右为X正方向,往下是Y正方向如下图: bounds和frame都是属于CGRect类型的结构体,系统的定义如下,包含一个CGPoint…...
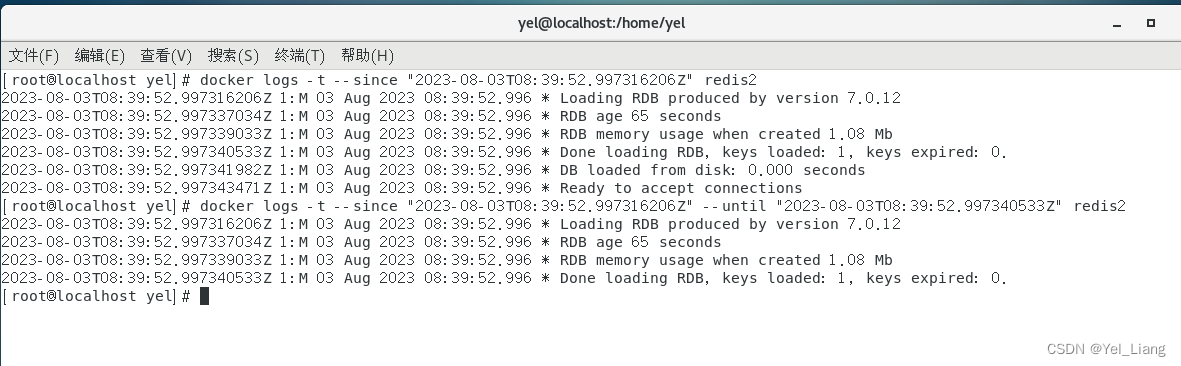
docker logs 使用说明
docker logs 可以查看某个容器内的日志情况。 前置参数说明 c_name容器名称 / 容器ID logs 获取容器的日志 , 命令如下: docker logs [options] c_name option参数: -n 查看最近多少条记录:docker logs -n 5 c_name--tail与-n 一样 &#…...
)
Ceph入门到精通-Ceph PG状态详细介绍(全)
本文主要介绍PG的各个状态,以及ceph故障过程中PG状态的转变。 Placement Group States(PG状态) creating Ceph is still creating the placement group. Ceph 仍在创建PG。activating The placement group is peered but not yet active.…...
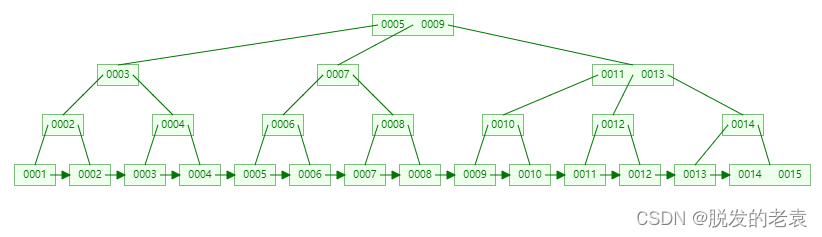
【数据结构】二叉树、二叉搜索树、平衡二叉树、红黑树、B树、B+树
概述 二叉树(Binary Tree):每个节点最多有两个子节点(左子节点和右子节点),没有限制节点的顺序。特点是简单直观,易于实现,但查找效率较低。 二叉搜索树(Binary Search…...

【JVM】(二)深入理解Java类加载机制与双亲委派模型
文章目录 前言一、类加载过程1.1 加载(Loading)1.2 验证(Verification)1.3 准备(Preparation)1.4 解析(Resolution)1.5 初始化(Initialization) 二、双亲委派…...
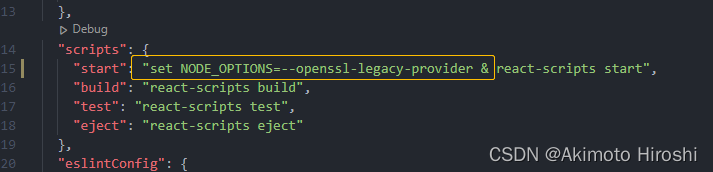
npm i 报错项目启动不了解决方法
1.场景 在另一台电脑低版本node环境跑的react项目,换到另一台电脑node18环境执行npm i时候报错 2.解决方法 脚本前加上set NODE_OPTIONS--openssl-legacy-provider...

【从零开始学习JAVA | 第三十七篇】初识多线程
目录 前言: 编辑 引入: 多线程: 什么是多线程: 多线程的意义: 多线程的应用场景: 总结: 前言: 本章节我们将开始学习多线程,多线程是一个很重要的知识点ÿ…...
微信新功能,你都知道吗?
近日iOS 微信8.0.40正式版来了,一起来看看有哪些变化? 1、朋友圈置顶 几个月前微信开始内测「朋友圈置顶」功能,从网友们的反馈来看,iOS 微信 8.0.40 似乎扩大了内测范围,更多用户可以体验到该功能了。 大家可以去自己…...
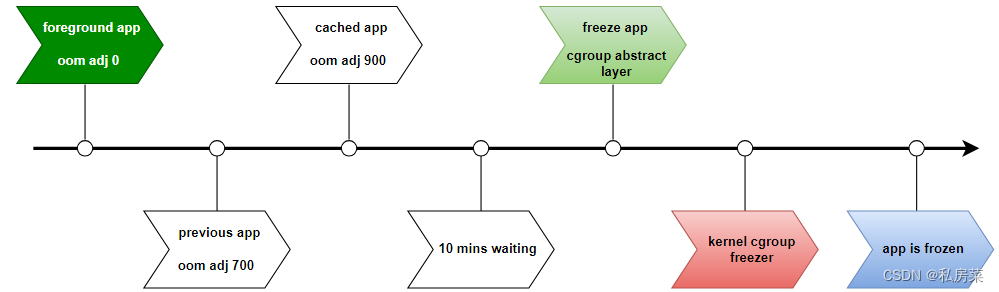
Android 中 app freezer 原理详解(二):S 版本
基于版本:Android S 0. 前言 在之前的两篇博文《Android 中app内存回收优化(一)》和 《Android 中app内存回收优化(二)》中详细剖析了 Android 中 app 内存优化的流程。这个机制的管理通过 CachedAppOptimizer 类管理,为什么叫这个名字,而不…...

Vue3_04_ref 函数和 reactive 函数
ref 函数 声明变量时,赋值的值要写在 ref() 函数中修改变量时,变量名.value xxx在模板中使用时可以省略掉 .value,直接使用变量名即可 <template><h1>一个人的信息</h1><h2>姓名:{{name}}</h2><…...
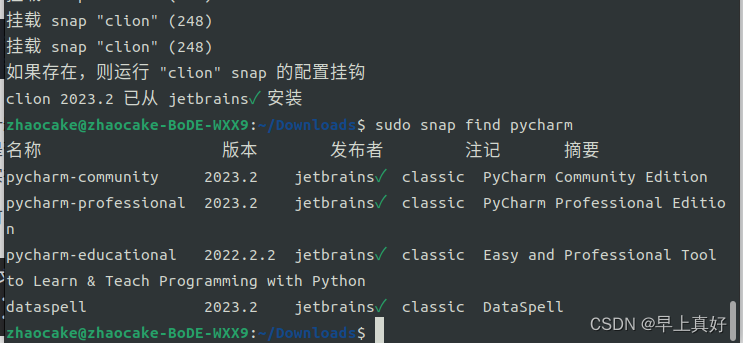
05 Ubuntu下安装.deb安装包方式安装vscode,snap安装Jetbrains产品等常用软件
使用deb包安装类型 deb包指的其实就是debian系统,ubuntu系统是基于debian系统的发行版。 一般我们会到需要的软件官网下载deb安装包,然后你既可以采用使用“软件安装”打开的方法来进行安装,也可以使用命令行进行安装。我推荐后者ÿ…...

性能测试jmeter连接数据库jdbc(sql server举例)
一、下载第三方工具包驱动数据库 1. 因为JMeter本身没有提供链接数据库的功能,所以我们需要借助第三方的工具包来实现。 (有这个jar包之后,jmeter可以发起jdbc请求,没有这个jar包,也有jdbc取样器,但不能发起…...
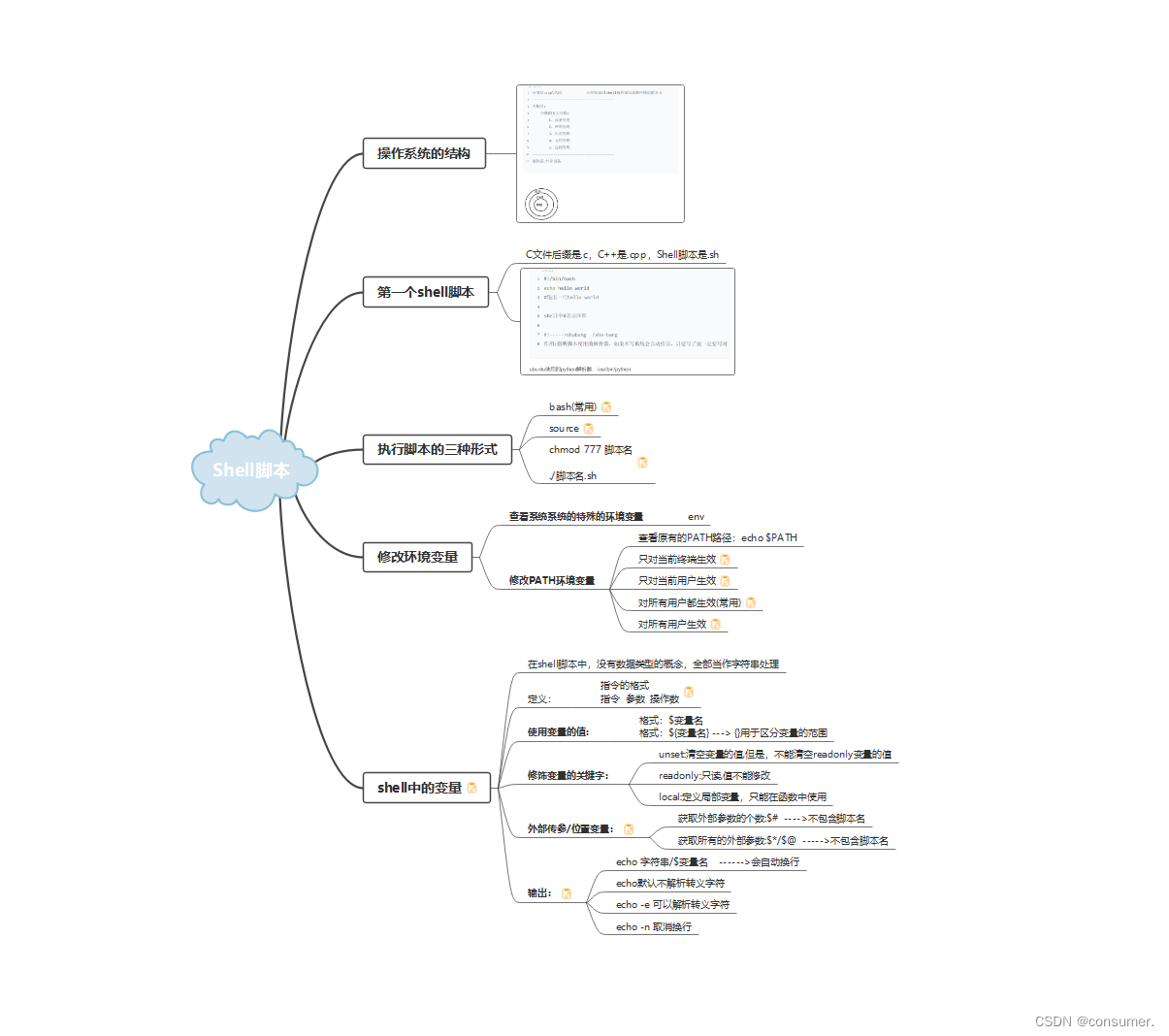
8.3 C高级 Shell脚本
写一个脚本,包含以下内容: 显示/etc/group文件中第五行的内容创建目录/home/ubuntu/copy切换工作路径到此目录赋值/etc/shadow到此目录,并重命名为test将当前目录中test的所属用户改为root将test中其他用户的权限改为没有任何权限 #!/bin/b…...

2023年华数杯A题
A 题 隔热材料的结构优化控制研究 新型隔热材料 A 具有优良的隔热特性,在航天、军工、石化、建筑、交通等 高科技领域中有着广泛的应用。 目前,由单根隔热材料 A 纤维编织成的织物,其热导率可以直接测出;但是 单根隔热材料 A 纤维…...

【零基础学Rust | 基础系列 | 函数,语句和表达式】函数的定义,使用和特性
文章标题 简介一,函数1,函数的定义2,函数的调用3,函数的参数4,函数的返回值 二,语句和表达式1,语句2,表达式 总结: 简介 在Rust编程中,函数,语句…...

加解密算法+压缩工具
sha256 工具类 package com.fanghui.vota.packages.util;import org.slf4j.Logger; import org.slf4j.LoggerFactory;import java.io.File; import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.IOException; import java.math.BigInteger…...

FeignClient接口的几种方式总结
FeignClient这个注解,已经封装了远程调用协议。在springboot的开发,或者微服务的开发过程中,我们需要跨服务调用,或者调用外部的接口,我们都可以使用FeignClient。 一、FeignClient介绍 FeignClient 注解是 Spring Cl…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
