LeetCode--HOT100题(18)
目录
- 题目描述:73. 矩阵置零(中等)
- 题目接口
- 解题思路1
- 代码
- 解题思路2
- 代码
- PS:
题目描述:73. 矩阵置零(中等)
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
LeetCode做题链接:LeetCode-矩阵置零
示例 1:
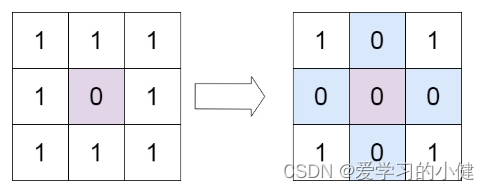
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
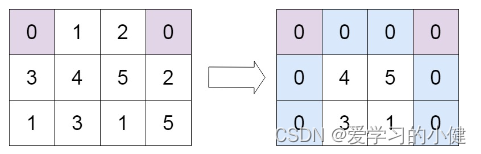
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
题目接口
class Solution {public void setZeroes(int[][] matrix) {}
}
解题思路1
方法一:使用标记数组
我们可以用两个布尔类型的标记数组(一个记录整行,一个记录整列)分别记录每一行和每一列是否有零出现,有的话将整行和整列置为true,然后再遍历一次数组将所有true的值对应的下标的数组换成0
代码
class Solution {public void setZeroes(int[][] matrix) {int colLen = matrix.length;int rowLen = matrix[0].length;boolean[] col = new boolean[colLen];boolean[] row = new boolean[rowLen];// 标记for (int i = 0; i < colLen; i++) {for (int j = 0; j < rowLen; j++) {if (matrix[i][j] == 0) {col[i] = true;row[j] = true;}}}// 遍历数组,将col,row为true的地方设为0for (int i = 0; i < colLen; i++) {for (int j = 0; j < rowLen; j++) {if (col[i] || row[j]) {matrix[i][j] = 0;}}}}
}
成功!

复杂度分析
时间复杂度:O(mn),其中 m 是矩阵的行数,n 是矩阵的列数。我们至多只需要遍历该矩阵两次。
空间复杂度:O(m+n),其中 m 是矩阵的行数,n 是矩阵的列数。我们需要分别记录每一行或每一列是否有零出现。
解题思路2

代码
class Solution {public void setZeroes(int[][] matrix) {int colLen = matrix.length;int rowLen = matrix[0].length;boolean flagRow = false; // 行boolean flagCol = false; // 列if (matrix[0][0] == 0) {// 如果第一个元素就是0,那 flagRow、flagCol直接置为true,不去遍历flagRow = flagCol = true;} else {for (int i = 0; i < rowLen; i++) {if (matrix[0][i] == 0) {flagRow = true; // 说明第一行有0,就直接为标true,然后退出break;}}for (int i = 0; i < colLen; i++) {if (matrix[i][0] == 0) {flagCol = true; // 说明第一列有0,就直接为标true,然后退出break;}}}// 开始标记,跟方法一类似,注意从1开始for (int i = 1; i < colLen; i++) {for (int j = 1; j < rowLen; j++) {if (matrix[i][j] == 0) {matrix[i][0] = 0;matrix[0][j] = 0;}}}// 遍历数组,将matrix[i][0] = 0 matrix[0][i] = 0 的行和列设为0,注意从1开始for (int i = 1; i < colLen; i++) {for (int j = 1; j < rowLen; j++) {if (matrix[i][0] == 0 || matrix[0][j] == 0) {matrix[i][j] = 0;}}}// 更新第一行与第一列if (flagRow) {for (int i = 0; i < rowLen; i++) {matrix[0][i] = 0;}}if (flagCol) {for (int i = 0; i < colLen; i++) {matrix[i][0] = 0;}}}
}
成功!

PS:
感谢您的阅读!如果您觉得本篇文章对您有所帮助,请给予博主一个赞喔~
相关文章:

LeetCode--HOT100题(18)
目录 题目描述:73. 矩阵置零(中等)题目接口解题思路1代码解题思路2代码 PS: 题目描述:73. 矩阵置零(中等) 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都…...

ES6的语法兼容IE浏览器
案例1 zdsxData.zdsxData.forEach(el>{let str <tr> <td><a href${el.url} target"_blank"><font color"#79EEFF">${el.sxms}</font></a></td> <td>${el.gjjd}</td> <td>${el.zrr}<…...

【opencv学习】鼠标回调函数、鼠标控制画矩形
#include <iostream> #include <opencv2/opencv.hpp> using namespace cv; #define WinDow "程序窗口"void MouseHandle(int event, int x, int y, int flags, void* param);//鼠标回调函数 void Drawrectangle(cv::Mat& img, cv::Rect box);//矩形绘…...

Typescript面试题
文章目录 了解过TS吗?使用ts写一个对象属性约束说一下typescript中的泛型如何在TS中对函数的返回值进行类型约束ts和js相比有什么区别 了解过TS吗? ts是一种基于静态类型检查的强类型语言 let num:number20 console.log(num) console.log("str&qu…...
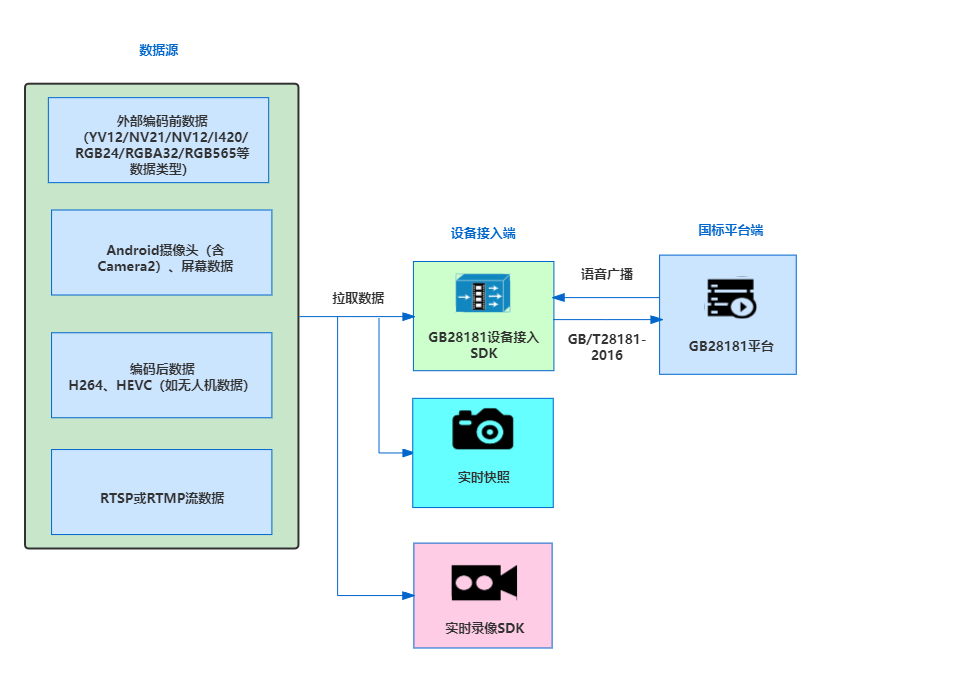
GB28181智能安全帽方案探究及技术实现
什么是智能安全帽? 智能安全帽是一种集成先进科技的安全帽,可基于GB28181规范,适用于铁路巡检、电力、石油化工等高风险行业的作业人员,以及消防、救援等紧急情况下的安全防护。 智能安全帽通常具有以下功能: 实时…...

【css】解决元素浮动溢出问题
如果一个元素比包含它的元素高,并且它是浮动的,它将“溢出”到其容器之外:然后可以向包含元素添加 overflow: auto;,来解决此问题: 代码: <!DOCTYPE html> <html> <head> <style>…...

SOC FPGA之流水灯设计
一、DS-5简介 Altera Soc EDS开发套件的核心是Altera版ARM Development Studio 5(DS-5)工具包,为SoC器件提供了完整的嵌入式开发环境、FPGA自适应调试和对Altera工具的兼容。 1.1 DS-5 eclipse破解 首先下载破解器 然后进入cmd运行,进入到破解器所在文…...

无涯教程-Lua - Iterators(迭代器)
迭代器是一种构造,使您可以遍历所谓的集合或集合的元素。在Lua中,这些集合通常引用表,这些表用于创建各种数据结构(如数组)。 通用迭代器 通用的 for 迭代器提供集合中每个元素的键值对。下面给出一个简单的示例。 array{"Lua",…...
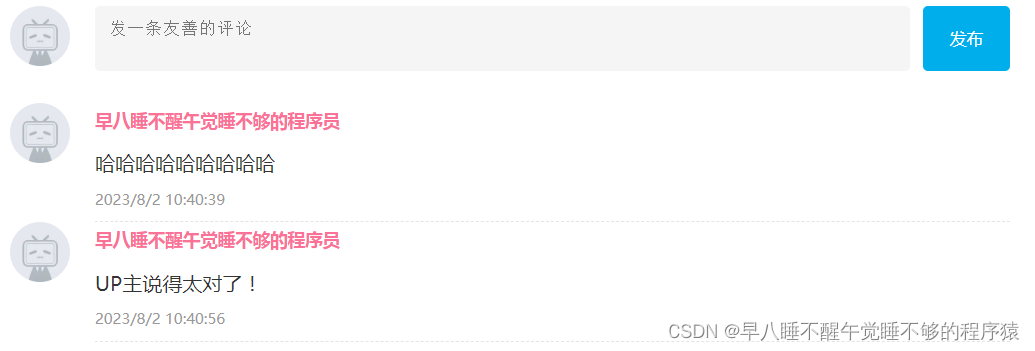
HTML+CSS+JavaScript:实现B站评论发布效果
一、需求 1、用户输入内容,输入框左下角实时显示输入字数 2、为避免用户输入时在内容左右两端误按多余的空格,在发送评论时,检测用户输入的内容左右两端是否带有空格,若有空格,发布时自动取消左右两端的空格 3、若用…...

实战 - 利用 ThreadLocal 线程局部变量实现数据缓存
文章目录 1. 利用 ThreadLocal 缓存 AssetBranchCache 数据1. 定义 AssetBranchCache 类2. 定义 BranchContext 类操作 AssetBranchCache 对象3. 配置拦截器实时更新和清除缓存数据4. 定义 SaasThreadContextDataHolderBranch 类持有 AssetBranchCache 对象5. 定义 SaasThreadC…...
wxwidgets Ribbon使用简单实例
// RibbonSample.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include <wx/wx.h> #include "wx/wxprec.h" #include "wx/app.h" #include "wx/frame.h" #include "wx/textctrl.h" #include "…...
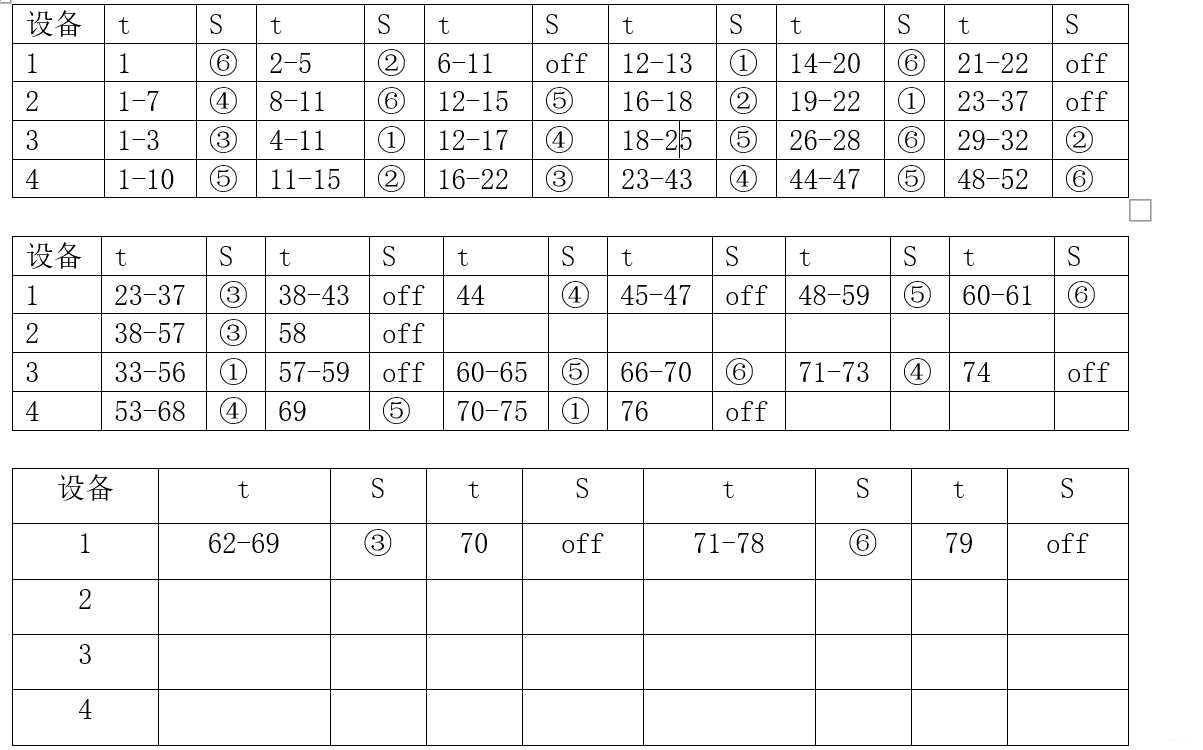
2023年第四届“华数杯”数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 0 赛题思路 (赛题出来以后第一时间在CSDN分享) 最短时间生产计划模型 该模型出现在好几个竞赛赛题上&#x…...

LeetCode404. 左叶子之和
404. 左叶子之和 文章目录 [404. 左叶子之和](https://leetcode.cn/problems/sum-of-left-leaves/)一、题目二、题解方法一:递归方法二:迭代 一、题目 给定二叉树的根节点 root ,返回所有左叶子之和。 示例 1: 输入: root [3,9…...
Nginx 高性能内存池 ----【学习笔记】
跟着这篇文章学习: c代码实现一个高性能内存池(超详细版本)_c 内存池库_linux大本营的博客-CSDN博客https://blog.csdn.net/qq_40989769/article/details/130874660以及这个视频学习: nginx的内存池_哔哩哔哩_bilibilihttps://w…...
iOS--frame和bounds
坐标系 首先,我们来看一下iOS特有的坐标系,在iOS坐标系中以左上角为坐标原点,往右为X正方向,往下是Y正方向如下图: bounds和frame都是属于CGRect类型的结构体,系统的定义如下,包含一个CGPoint…...
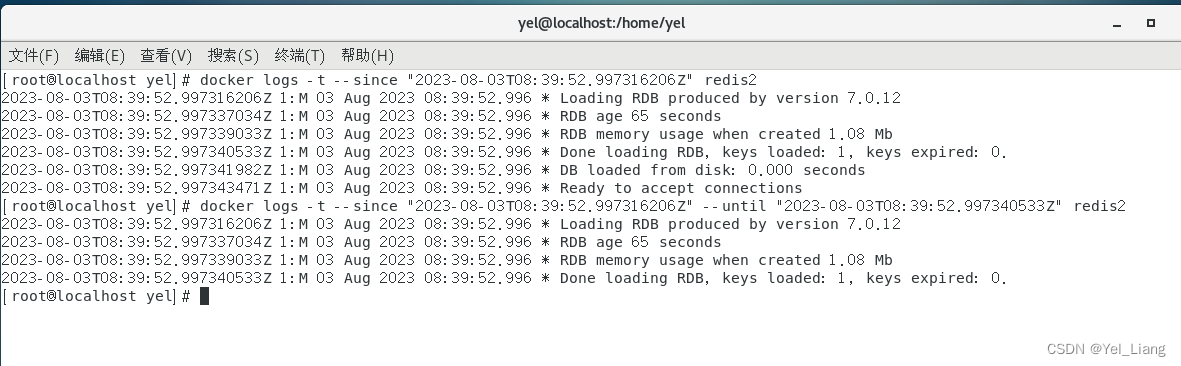
docker logs 使用说明
docker logs 可以查看某个容器内的日志情况。 前置参数说明 c_name容器名称 / 容器ID logs 获取容器的日志 , 命令如下: docker logs [options] c_name option参数: -n 查看最近多少条记录:docker logs -n 5 c_name--tail与-n 一样 &#…...
)
Ceph入门到精通-Ceph PG状态详细介绍(全)
本文主要介绍PG的各个状态,以及ceph故障过程中PG状态的转变。 Placement Group States(PG状态) creating Ceph is still creating the placement group. Ceph 仍在创建PG。activating The placement group is peered but not yet active.…...
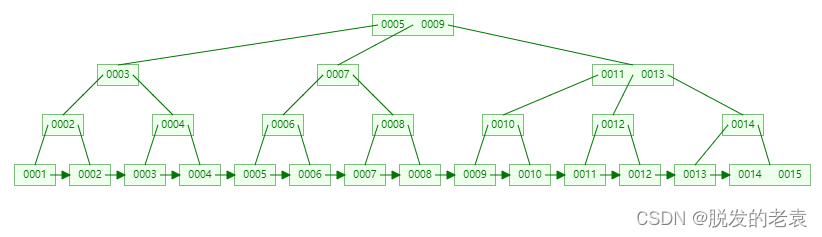
【数据结构】二叉树、二叉搜索树、平衡二叉树、红黑树、B树、B+树
概述 二叉树(Binary Tree):每个节点最多有两个子节点(左子节点和右子节点),没有限制节点的顺序。特点是简单直观,易于实现,但查找效率较低。 二叉搜索树(Binary Search…...

【JVM】(二)深入理解Java类加载机制与双亲委派模型
文章目录 前言一、类加载过程1.1 加载(Loading)1.2 验证(Verification)1.3 准备(Preparation)1.4 解析(Resolution)1.5 初始化(Initialization) 二、双亲委派…...
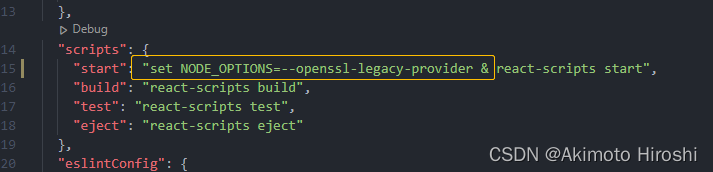
npm i 报错项目启动不了解决方法
1.场景 在另一台电脑低版本node环境跑的react项目,换到另一台电脑node18环境执行npm i时候报错 2.解决方法 脚本前加上set NODE_OPTIONS--openssl-legacy-provider...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
