【机器学习】Feature Engineering and Polynomial Regression
Feature Engineering and Polynomial Regression
- 1. 多项式特征
- 2. 选择特征
- 3. 缩放特征
- 4. 复杂函数
- 附录
首先,导入所需的库:
import numpy as np
import matplotlib.pyplot as plt
from lab_utils_multi import zscore_normalize_features, run_gradient_descent_feng
np.set_printoptions(precision=2) # reduced display precision on numpy arrays
线性回归模型表示为:
f w , b = w 0 x 0 + w 1 x 1 + . . . + w n − 1 x n − 1 + b (1) f_{\mathbf{w},b} = w_0x_0 + w_1x_1+ ... + w_{n-1}x_{n-1} + b \tag{1} fw,b=w0x0+w1x1+...+wn−1xn−1+b(1)
思考一下,如果特征是非线性的或者是特征的结合,线性模型不能拟合,那该怎么办?
1. 多项式特征
尝试使用目前已知的知识来拟合非线性曲线。我们将从一个简单的二次方程开始: y = 1 + x 2 y = 1+x^2 y=1+x2
# create target data
x = np.arange(0, 20, 1)
y = 1 + x**2
X = x.reshape(-1, 1)model_w,model_b = run_gradient_descent_feng(X,y,iterations=1000, alpha = 1e-2)plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("no feature engineering")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("X"); plt.ylabel("y"); plt.legend(); plt.show()

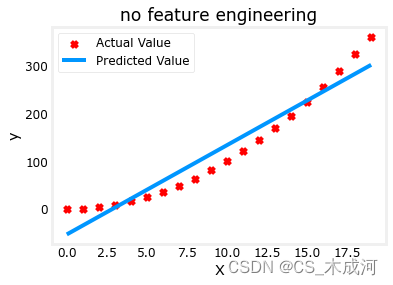
正如所期待的那样,线性方程明显不合适。如果将X 换成 X**2会如何?
# create target data
x = np.arange(0, 20, 1)
y = 1 + x**2# Engineer features
X = x**2 #<-- added engineered feature
X = X.reshape(-1, 1) #X should be a 2-D Matrix
model_w,model_b = run_gradient_descent_feng(X, y, iterations=10000, alpha = 1e-5)plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Added x**2 feature")
plt.plot(x, np.dot(X,model_w) + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()

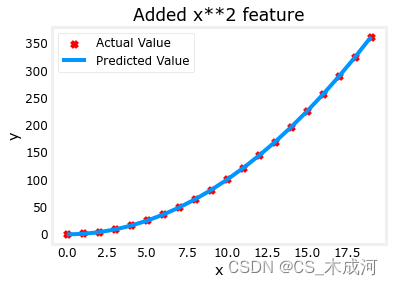
梯度下降将 w , b \mathbf{w},b w,b的初始值修改为 (1.0,0.049) ,即模型方程 y = 1 ∗ x 0 2 + 0.049 y=1*x_0^2+0.049 y=1∗x02+0.049, 这非常接近目标方程 y = 1 ∗ x 0 2 + 1 y=1*x_0^2+1 y=1∗x02+1.
2. 选择特征
从上面可以知道, x 2 x^2 x2是需要的。接下来我们尝试: y = w 0 x 0 + w 1 x 1 2 + w 2 x 2 3 + b y=w_0x_0 + w_1x_1^2 + w_2x_2^3+b y=w0x0+w1x12+w2x23+b
# create target data
x = np.arange(0, 20, 1)
y = x**2# engineer features .
X = np.c_[x, x**2, x**3] #<-- added engineered feature
model_w,model_b = run_gradient_descent_feng(X, y, iterations=10000, alpha=1e-7)plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("x, x**2, x**3 features")
plt.plot(x, X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()

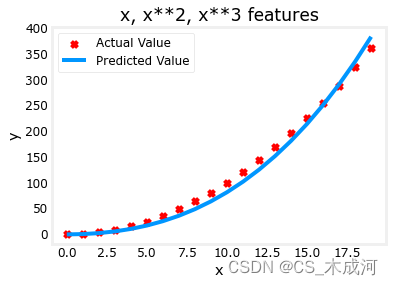
w \mathbf{w} w的值为 [0.08 0.54 0.03] , b 为 0.0106。训练后的模型为:
0.08 x + 0.54 x 2 + 0.03 x 3 + 0.0106 0.08x + 0.54x^2 + 0.03x^3 + 0.0106 0.08x+0.54x2+0.03x3+0.0106
梯度下降通过相对于其他项增加 w 1 w_1 w1项,强调了最适合 x 2 x^2 x2的数据。如果运行很长时间,它将继续减少其他项的影响。梯度下降通过强调其相关参数来为我们选择“正确”的特征。
- 一般来讲,特征被重新缩放,因此它们可以相互比较
- 权重值越小意味着不太重要的特征,在极端情况下,当权重变为零或非常接近零时,相关特征在将模型拟合到数据中是有用的。
- 如上所述,拟合后,与 x 2 x^2 x2功能相关的权重远大于 x x x或 x 3 x^3 x3的权重,因为它在拟合数据时最有用。
多项式特征是根据它们与目标数据的匹配程度来选择的。一旦我们创建了新特征,我们仍然使用线性回归。最好的特征将相对于目标呈线性关系。下面通过一个例子来理解这一点。
# create target data
x = np.arange(0, 20, 1)
y = x**2# engineer features .
X = np.c_[x, x**2, x**3] #<-- added engineered feature
X_features = ['x','x^2','x^3']
fig,ax=plt.subplots(1, 3, figsize=(12, 3), sharey=True)
for i in range(len(ax)):ax[i].scatter(X[:,i],y)ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("y")
plt.show()
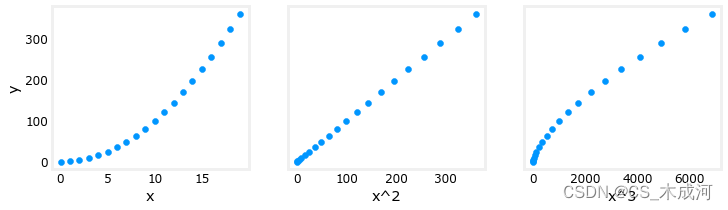
很明显, x 2 x^2 x2特征映射到目标值 y y y是线性的。线性回归可以使用该特征轻松生成模型。
3. 缩放特征
如果数据集具有显着不同尺度的特征,则应该应用特征缩放来加速梯度下降。在上面的例子中,有 x x x, x 2 x^2 x2 和 x 3 x^3 x3,这自然会有非常不同的规模。接下来将 Z-score 归一化应用到示例中。
# create target data
x = np.arange(0,20,1)
X = np.c_[x, x**2, x**3]
print(f"Peak to Peak range by column in Raw X:{np.ptp(X,axis=0)}")# add mean_normalization
X = zscore_normalize_features(X)
print(f"Peak to Peak range by column in Normalized X:{np.ptp(X,axis=0)}")

使用更大的alpha值运行:
x = np.arange(0,20,1)
y = x**2X = np.c_[x, x**2, x**3]
X = zscore_normalize_features(X) model_w, model_b = run_gradient_descent_feng(X, y, iterations=100000, alpha=1e-1)plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Normalized x x**2, x**3 feature")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()

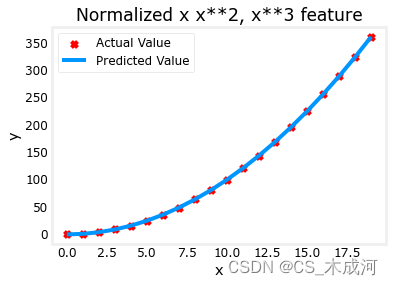
特征缩放使得收敛速度更快。梯度下降过程中, x 2 x^2 x2 是最受强调的, x 3 x^3 x3项几乎被消除。
4. 复杂函数
通过特征工程,甚至可以对相当复杂的函数进行建模:
x = np.arange(0,20,1)
y = np.cos(x/2)X = np.c_[x, x**2, x**3,x**4, x**5, x**6, x**7, x**8, x**9, x**10, x**11, x**12, x**13]
X = zscore_normalize_features(X) model_w,model_b = run_gradient_descent_feng(X, y, iterations=1000000, alpha = 1e-1)plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Normalized x x**2, x**3 feature")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()

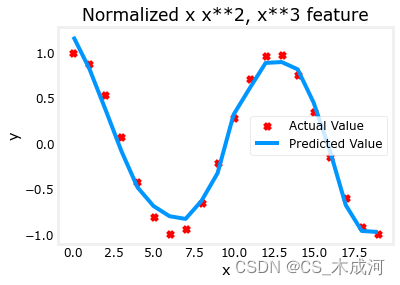
附录
lab_utils_multi.py源码:
import numpy as np
import copy
import math
from scipy.stats import norm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib.ticker import MaxNLocator
dlblue = '#0096ff'; dlorange = '#FF9300'; dldarkred='#C00000'; dlmagenta='#FF40FF'; dlpurple='#7030A0';
plt.style.use('./deeplearning.mplstyle')def load_data_multi():data = np.loadtxt("data/ex1data2.txt", delimiter=',')X = data[:,:2]y = data[:,2]return X, y##########################################################
# Plotting Routines
##########################################################def plt_house_x(X, y,f_wb=None, ax=None):''' plot house with aXis '''if not ax:fig, ax = plt.subplots(1,1)ax.scatter(X, y, marker='x', c='r', label="Actual Value")ax.set_title("Housing Prices")ax.set_ylabel('Price (in 1000s of dollars)')ax.set_xlabel(f'Size (1000 sqft)')if f_wb is not None:ax.plot(X, f_wb, c=dlblue, label="Our Prediction")ax.legend()def mk_cost_lines(x,y,w,b, ax):''' makes vertical cost lines'''cstr = "cost = (1/2m)*1000*("ctot = 0label = 'cost for point'for p in zip(x,y):f_wb_p = w*p[0]+bc_p = ((f_wb_p - p[1])**2)/2c_p_txt = c_p/1000ax.vlines(p[0], p[1],f_wb_p, lw=3, color=dlpurple, ls='dotted', label=label)label='' #just onecxy = [p[0], p[1] + (f_wb_p-p[1])/2]ax.annotate(f'{c_p_txt:0.0f}', xy=cxy, xycoords='data',color=dlpurple, xytext=(5, 0), textcoords='offset points')cstr += f"{c_p_txt:0.0f} +"ctot += c_pctot = ctot/(len(x))cstr = cstr[:-1] + f") = {ctot:0.0f}"ax.text(0.15,0.02,cstr, transform=ax.transAxes, color=dlpurple)def inbounds(a,b,xlim,ylim):xlow,xhigh = xlimylow,yhigh = ylimax, ay = abx, by = bif (ax > xlow and ax < xhigh) and (bx > xlow and bx < xhigh) \and (ay > ylow and ay < yhigh) and (by > ylow and by < yhigh):return(True)else:return(False)from mpl_toolkits.mplot3d import axes3d
def plt_contour_wgrad(x, y, hist, ax, w_range=[-100, 500, 5], b_range=[-500, 500, 5], contours = [0.1,50,1000,5000,10000,25000,50000], resolution=5, w_final=200, b_final=100,step=10 ):b0,w0 = np.meshgrid(np.arange(*b_range),np.arange(*w_range))z=np.zeros_like(b0)n,_ = w0.shapefor i in range(w0.shape[0]):for j in range(w0.shape[1]):z[i][j] = compute_cost(x, y, w0[i][j], b0[i][j] )CS = ax.contour(w0, b0, z, contours, linewidths=2,colors=[dlblue, dlorange, dldarkred, dlmagenta, dlpurple]) ax.clabel(CS, inline=1, fmt='%1.0f', fontsize=10)ax.set_xlabel("w"); ax.set_ylabel("b")ax.set_title('Contour plot of cost J(w,b), vs b,w with path of gradient descent')w = w_final; b=b_finalax.hlines(b, ax.get_xlim()[0],w, lw=2, color=dlpurple, ls='dotted')ax.vlines(w, ax.get_ylim()[0],b, lw=2, color=dlpurple, ls='dotted')base = hist[0]for point in hist[0::step]:edist = np.sqrt((base[0] - point[0])**2 + (base[1] - point[1])**2)if(edist > resolution or point==hist[-1]):if inbounds(point,base, ax.get_xlim(),ax.get_ylim()):plt.annotate('', xy=point, xytext=base,xycoords='data',arrowprops={'arrowstyle': '->', 'color': 'r', 'lw': 3},va='center', ha='center')base=pointreturn# plots p1 vs p2. Prange is an array of entries [min, max, steps]. In feature scaling lab.
def plt_contour_multi(x, y, w, b, ax, prange, p1, p2, title="", xlabel="", ylabel=""): contours = [1e2, 2e2,3e2,4e2, 5e2, 6e2, 7e2,8e2,1e3, 1.25e3,1.5e3, 1e4, 1e5, 1e6, 1e7]px,py = np.meshgrid(np.linspace(*(prange[p1])),np.linspace(*(prange[p2])))z=np.zeros_like(px)n,_ = px.shapefor i in range(px.shape[0]):for j in range(px.shape[1]):w_ij = wb_ij = bif p1 <= 3: w_ij[p1] = px[i,j]if p1 == 4: b_ij = px[i,j]if p2 <= 3: w_ij[p2] = py[i,j]if p2 == 4: b_ij = py[i,j]z[i][j] = compute_cost(x, y, w_ij, b_ij )CS = ax.contour(px, py, z, contours, linewidths=2,colors=[dlblue, dlorange, dldarkred, dlmagenta, dlpurple]) ax.clabel(CS, inline=1, fmt='%1.2e', fontsize=10)ax.set_xlabel(xlabel); ax.set_ylabel(ylabel)ax.set_title(title, fontsize=14)def plt_equal_scale(X_train, X_norm, y_train):fig,ax = plt.subplots(1,2,figsize=(12,5))prange = [[ 0.238-0.045, 0.238+0.045, 50],[-25.77326319-0.045, -25.77326319+0.045, 50],[-50000, 0, 50],[-1500, 0, 50],[0, 200000, 50]]w_best = np.array([0.23844318, -25.77326319, -58.11084634, -1.57727192])b_best = 235plt_contour_multi(X_train, y_train, w_best, b_best, ax[0], prange, 0, 1, title='Unnormalized, J(w,b), vs w[0],w[1]',xlabel= "w[0] (size(sqft))", ylabel="w[1] (# bedrooms)")#w_best = np.array([111.1972, -16.75480051, -28.51530411, -37.17305735])b_best = 376.949151515151prange = [[ 111-50, 111+50, 75],[-16.75-50,-16.75+50, 75],[-28.5-8, -28.5+8, 50],[-37.1-16,-37.1+16, 50],[376-150, 376+150, 50]]plt_contour_multi(X_norm, y_train, w_best, b_best, ax[1], prange, 0, 1, title='Normalized, J(w,b), vs w[0],w[1]',xlabel= "w[0] (normalized size(sqft))", ylabel="w[1] (normalized # bedrooms)")fig.suptitle("Cost contour with equal scale", fontsize=18)#plt.tight_layout(rect=(0,0,1.05,1.05))fig.tight_layout(rect=(0,0,1,0.95))plt.show()def plt_divergence(p_hist, J_hist, x_train,y_train):x=np.zeros(len(p_hist))y=np.zeros(len(p_hist))v=np.zeros(len(p_hist))for i in range(len(p_hist)):x[i] = p_hist[i][0]y[i] = p_hist[i][1]v[i] = J_hist[i]fig = plt.figure(figsize=(12,5))plt.subplots_adjust( wspace=0 )gs = fig.add_gridspec(1, 5)fig.suptitle(f"Cost escalates when learning rate is too large")#===============# First subplot#===============ax = fig.add_subplot(gs[:2], )# Print w vs cost to see minimumfix_b = 100w_array = np.arange(-70000, 70000, 1000)cost = np.zeros_like(w_array)for i in range(len(w_array)):tmp_w = w_array[i]cost[i] = compute_cost(x_train, y_train, tmp_w, fix_b)ax.plot(w_array, cost)ax.plot(x,v, c=dlmagenta)ax.set_title("Cost vs w, b set to 100")ax.set_ylabel('Cost')ax.set_xlabel('w')ax.xaxis.set_major_locator(MaxNLocator(2)) #===============# Second Subplot#===============tmp_b,tmp_w = np.meshgrid(np.arange(-35000, 35000, 500),np.arange(-70000, 70000, 500))z=np.zeros_like(tmp_b)for i in range(tmp_w.shape[0]):for j in range(tmp_w.shape[1]):z[i][j] = compute_cost(x_train, y_train, tmp_w[i][j], tmp_b[i][j] )ax = fig.add_subplot(gs[2:], projection='3d')ax.plot_surface(tmp_w, tmp_b, z, alpha=0.3, color=dlblue)ax.xaxis.set_major_locator(MaxNLocator(2)) ax.yaxis.set_major_locator(MaxNLocator(2)) ax.set_xlabel('w', fontsize=16)ax.set_ylabel('b', fontsize=16)ax.set_zlabel('\ncost', fontsize=16)plt.title('Cost vs (b, w)')# Customize the view angle ax.view_init(elev=20., azim=-65)ax.plot(x, y, v,c=dlmagenta)return# draw derivative line
# y = m*(x - x1) + y1
def add_line(dj_dx, x1, y1, d, ax):x = np.linspace(x1-d, x1+d,50)y = dj_dx*(x - x1) + y1ax.scatter(x1, y1, color=dlblue, s=50)ax.plot(x, y, '--', c=dldarkred,zorder=10, linewidth = 1)xoff = 30 if x1 == 200 else 10ax.annotate(r"$\frac{\partial J}{\partial w}$ =%d" % dj_dx, fontsize=14,xy=(x1, y1), xycoords='data',xytext=(xoff, 10), textcoords='offset points',arrowprops=dict(arrowstyle="->"),horizontalalignment='left', verticalalignment='top')def plt_gradients(x_train,y_train, f_compute_cost, f_compute_gradient):#===============# First subplot#===============fig,ax = plt.subplots(1,2,figsize=(12,4))# Print w vs cost to see minimumfix_b = 100w_array = np.linspace(-100, 500, 50)w_array = np.linspace(0, 400, 50)cost = np.zeros_like(w_array)for i in range(len(w_array)):tmp_w = w_array[i]cost[i] = f_compute_cost(x_train, y_train, tmp_w, fix_b)ax[0].plot(w_array, cost,linewidth=1)ax[0].set_title("Cost vs w, with gradient; b set to 100")ax[0].set_ylabel('Cost')ax[0].set_xlabel('w')# plot lines for fixed b=100for tmp_w in [100,200,300]:fix_b = 100dj_dw,dj_db = f_compute_gradient(x_train, y_train, tmp_w, fix_b )j = f_compute_cost(x_train, y_train, tmp_w, fix_b)add_line(dj_dw, tmp_w, j, 30, ax[0])#===============# Second Subplot#===============tmp_b,tmp_w = np.meshgrid(np.linspace(-200, 200, 10), np.linspace(-100, 600, 10))U = np.zeros_like(tmp_w)V = np.zeros_like(tmp_b)for i in range(tmp_w.shape[0]):for j in range(tmp_w.shape[1]):U[i][j], V[i][j] = f_compute_gradient(x_train, y_train, tmp_w[i][j], tmp_b[i][j] )X = tmp_wY = tmp_bn=-2color_array = np.sqrt(((V-n)/2)**2 + ((U-n)/2)**2)ax[1].set_title('Gradient shown in quiver plot')Q = ax[1].quiver(X, Y, U, V, color_array, units='width', )qk = ax[1].quiverkey(Q, 0.9, 0.9, 2, r'$2 \frac{m}{s}$', labelpos='E',coordinates='figure')ax[1].set_xlabel("w"); ax[1].set_ylabel("b")def norm_plot(ax, data):scale = (np.max(data) - np.min(data))*0.2x = np.linspace(np.min(data)-scale,np.max(data)+scale,50)_,bins, _ = ax.hist(data, x, color="xkcd:azure")#ax.set_ylabel("Count")mu = np.mean(data); std = np.std(data); dist = norm.pdf(bins, loc=mu, scale = std)axr = ax.twinx()axr.plot(bins,dist, color = "orangered", lw=2)axr.set_ylim(bottom=0)axr.axis('off')def plot_cost_i_w(X,y,hist):ws = np.array([ p[0] for p in hist["params"]])rng = max(abs(ws[:,0].min()),abs(ws[:,0].max()))wr = np.linspace(-rng+0.27,rng+0.27,20)cst = [compute_cost(X,y,np.array([wr[i],-32, -67, -1.46]), 221) for i in range(len(wr))]fig,ax = plt.subplots(1,2,figsize=(12,3))ax[0].plot(hist["iter"], (hist["cost"])); ax[0].set_title("Cost vs Iteration")ax[0].set_xlabel("iteration"); ax[0].set_ylabel("Cost")ax[1].plot(wr, cst); ax[1].set_title("Cost vs w[0]")ax[1].set_xlabel("w[0]"); ax[1].set_ylabel("Cost")ax[1].plot(ws[:,0],hist["cost"])plt.show()##########################################################
# Regression Routines
##########################################################def compute_gradient_matrix(X, y, w, b): """Computes the gradient for linear regression Args:X : (array_like Shape (m,n)) variable such as house size y : (array_like Shape (m,1)) actual value w : (array_like Shape (n,1)) Values of parameters of the model b : (scalar ) Values of parameter of the model Returnsdj_dw: (array_like Shape (n,1)) The gradient of the cost w.r.t. the parameters w. dj_db: (scalar) The gradient of the cost w.r.t. the parameter b. """m,n = X.shapef_wb = X @ w + b e = f_wb - y dj_dw = (1/m) * (X.T @ e) dj_db = (1/m) * np.sum(e) return dj_db,dj_dw#Function to calculate the cost
def compute_cost_matrix(X, y, w, b, verbose=False):"""Computes the gradient for linear regression Args:X : (array_like Shape (m,n)) variable such as house size y : (array_like Shape (m,)) actual value w : (array_like Shape (n,)) parameters of the model b : (scalar ) parameter of the model verbose : (Boolean) If true, print out intermediate value f_wbReturnscost: (scalar) """ m,n = X.shape# calculate f_wb for all examples.f_wb = X @ w + b # calculate costtotal_cost = (1/(2*m)) * np.sum((f_wb-y)**2)if verbose: print("f_wb:")if verbose: print(f_wb)return total_cost# Loop version of multi-variable compute_cost
def compute_cost(X, y, w, b): """compute costArgs:X : (ndarray): Shape (m,n) matrix of examples with multiple featuresw : (ndarray): Shape (n) parameters for prediction b : (scalar): parameter for prediction Returnscost: (scalar) cost"""m = X.shape[0]cost = 0.0for i in range(m): f_wb_i = np.dot(X[i],w) + b cost = cost + (f_wb_i - y[i])**2 cost = cost/(2*m) return(np.squeeze(cost)) def compute_gradient(X, y, w, b): """Computes the gradient for linear regression Args:X : (ndarray Shape (m,n)) matrix of examples y : (ndarray Shape (m,)) target value of each examplew : (ndarray Shape (n,)) parameters of the model b : (scalar) parameter of the model Returnsdj_dw : (ndarray Shape (n,)) The gradient of the cost w.r.t. the parameters w. dj_db : (scalar) The gradient of the cost w.r.t. the parameter b. """m,n = X.shape #(number of examples, number of features)dj_dw = np.zeros((n,))dj_db = 0.for i in range(m): err = (np.dot(X[i], w) + b) - y[i] for j in range(n): dj_dw[j] = dj_dw[j] + err * X[i,j] dj_db = dj_db + err dj_dw = dj_dw/m dj_db = dj_db/m return dj_db,dj_dw#This version saves more values and is more verbose than the assigment versons
def gradient_descent_houses(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): """Performs batch gradient descent to learn theta. Updates theta by taking num_iters gradient steps with learning rate alphaArgs:X : (array_like Shape (m,n) matrix of examples y : (array_like Shape (m,)) target value of each examplew_in : (array_like Shape (n,)) Initial values of parameters of the modelb_in : (scalar) Initial value of parameter of the modelcost_function: function to compute costgradient_function: function to compute the gradientalpha : (float) Learning ratenum_iters : (int) number of iterations to run gradient descentReturnsw : (array_like Shape (n,)) Updated values of parameters of the model afterrunning gradient descentb : (scalar) Updated value of parameter of the model afterrunning gradient descent"""# number of training examplesm = len(X)# An array to store values at each iteration primarily for graphing laterhist={}hist["cost"] = []; hist["params"] = []; hist["grads"]=[]; hist["iter"]=[];w = copy.deepcopy(w_in) #avoid modifying global w within functionb = b_insave_interval = np.ceil(num_iters/10000) # prevent resource exhaustion for long runsprint(f"Iteration Cost w0 w1 w2 w3 b djdw0 djdw1 djdw2 djdw3 djdb ")print(f"---------------------|--------|--------|--------|--------|--------|--------|--------|--------|--------|--------|")for i in range(num_iters):# Calculate the gradient and update the parametersdj_db,dj_dw = gradient_function(X, y, w, b) # Update Parameters using w, b, alpha and gradientw = w - alpha * dj_dw b = b - alpha * dj_db # Save cost J,w,b at each save interval for graphingif i == 0 or i % save_interval == 0: hist["cost"].append(cost_function(X, y, w, b))hist["params"].append([w,b])hist["grads"].append([dj_dw,dj_db])hist["iter"].append(i)# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10) == 0:#print(f"Iteration {i:4d}: Cost {cost_function(X, y, w, b):8.2f} ")cst = cost_function(X, y, w, b)print(f"{i:9d} {cst:0.5e} {w[0]: 0.1e} {w[1]: 0.1e} {w[2]: 0.1e} {w[3]: 0.1e} {b: 0.1e} {dj_dw[0]: 0.1e} {dj_dw[1]: 0.1e} {dj_dw[2]: 0.1e} {dj_dw[3]: 0.1e} {dj_db: 0.1e}")return w, b, hist #return w,b and history for graphingdef run_gradient_descent(X,y,iterations=1000, alpha = 1e-6):m,n = X.shape# initialize parametersinitial_w = np.zeros(n)initial_b = 0# run gradient descentw_out, b_out, hist_out = gradient_descent_houses(X ,y, initial_w, initial_b,compute_cost, compute_gradient_matrix, alpha, iterations)print(f"w,b found by gradient descent: w: {w_out}, b: {b_out:0.2f}")return(w_out, b_out, hist_out)# compact extaction of hist data
#x = hist["iter"]
#J = np.array([ p for p in hist["cost"]])
#ws = np.array([ p[0] for p in hist["params"]])
#dj_ws = np.array([ p[0] for p in hist["grads"]])#bs = np.array([ p[1] for p in hist["params"]]) def run_gradient_descent_feng(X,y,iterations=1000, alpha = 1e-6):m,n = X.shape# initialize parametersinitial_w = np.zeros(n)initial_b = 0# run gradient descentw_out, b_out, hist_out = gradient_descent(X ,y, initial_w, initial_b,compute_cost, compute_gradient_matrix, alpha, iterations)print(f"w,b found by gradient descent: w: {w_out}, b: {b_out:0.4f}")return(w_out, b_out)def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): """Performs batch gradient descent to learn theta. Updates theta by taking num_iters gradient steps with learning rate alphaArgs:X : (array_like Shape (m,n) matrix of examples y : (array_like Shape (m,)) target value of each examplew_in : (array_like Shape (n,)) Initial values of parameters of the modelb_in : (scalar) Initial value of parameter of the modelcost_function: function to compute costgradient_function: function to compute the gradientalpha : (float) Learning ratenum_iters : (int) number of iterations to run gradient descentReturnsw : (array_like Shape (n,)) Updated values of parameters of the model afterrunning gradient descentb : (scalar) Updated value of parameter of the model afterrunning gradient descent"""# number of training examplesm = len(X)# An array to store values at each iteration primarily for graphing laterhist={}hist["cost"] = []; hist["params"] = []; hist["grads"]=[]; hist["iter"]=[];w = copy.deepcopy(w_in) #avoid modifying global w within functionb = b_insave_interval = np.ceil(num_iters/10000) # prevent resource exhaustion for long runsfor i in range(num_iters):# Calculate the gradient and update the parametersdj_db,dj_dw = gradient_function(X, y, w, b) # Update Parameters using w, b, alpha and gradientw = w - alpha * dj_dw b = b - alpha * dj_db # Save cost J,w,b at each save interval for graphingif i == 0 or i % save_interval == 0: hist["cost"].append(cost_function(X, y, w, b))hist["params"].append([w,b])hist["grads"].append([dj_dw,dj_db])hist["iter"].append(i)# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10) == 0:#print(f"Iteration {i:4d}: Cost {cost_function(X, y, w, b):8.2f} ")cst = cost_function(X, y, w, b)print(f"Iteration {i:9d}, Cost: {cst:0.5e}")return w, b, hist #return w,b and history for graphingdef load_house_data():data = np.loadtxt("./data/houses.txt", delimiter=',', skiprows=1)X = data[:,:4]y = data[:,4]return X, ydef zscore_normalize_features(X,rtn_ms=False):"""returns z-score normalized X by columnArgs:X : (numpy array (m,n)) ReturnsX_norm: (numpy array (m,n)) input normalized by column"""mu = np.mean(X,axis=0) sigma = np.std(X,axis=0)X_norm = (X - mu)/sigma if rtn_ms:return(X_norm, mu, sigma)else:return(X_norm)
相关文章:

【机器学习】Feature Engineering and Polynomial Regression
Feature Engineering and Polynomial Regression 1. 多项式特征2. 选择特征3. 缩放特征4. 复杂函数附录 首先,导入所需的库: import numpy as np import matplotlib.pyplot as plt from lab_utils_multi import zscore_normalize_features, run_gradien…...

Rust- 变量绑定
In Rust, you bind values to a variable name using the let keyword. This is often referred to as “variable binding” because it’s like binding a name to a value. Here’s a simple example: let x 5;In this example, x is bound to the value 5. By default, …...
向“数”而“深”,联想凌拓的“破局求变”底气何来?
前言:要赢得更多机遇,“破局求变”尤为重要。 【全球存储观察 | 热点关注】2019年2月25日,承袭联想集团与NetApp的“双基因”,联想凌拓正式成立。历经四年多的发展,联想凌拓已成为中国企业级数据管理领域的…...
pytorch实战-图像分类(二)(模型训练及验证)(基于迁移学习(理解+代码))
目录 1.迁移学习概念 2.数据预处理 3.训练模型(基于迁移学习) 3.1选择网络,这里用resnet 3.2如果用GPU训练,需要加入以下代码 3.3卷积层冻结模块 3.4加载resnet152模 3.5解释initialize_model函数 3.6迁移学习网络搭建 3.…...
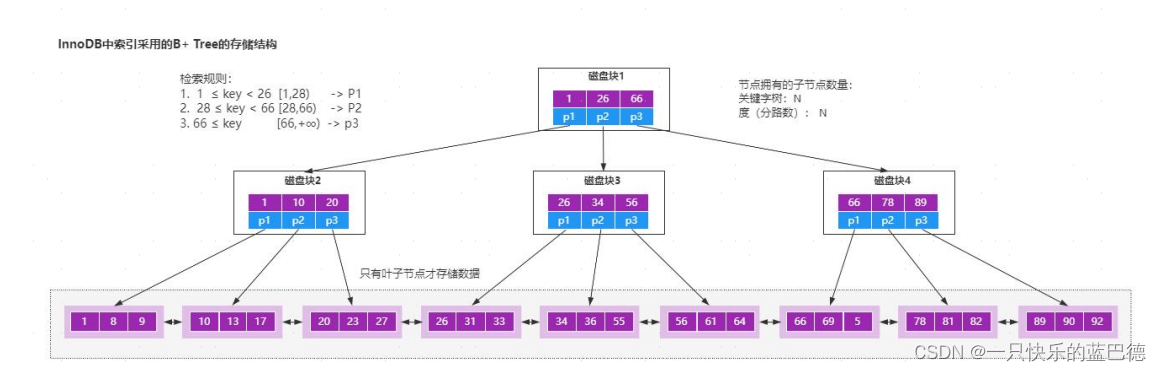
b 树和 b+树的理解
项目场景: 图灵奖获得者(Niklaus Wirth )说过: 程序 数据结构 算法, 也就说我们无时无刻 都在和数据结构打交道。 只是作为 Java 开发,由于技术体系的成熟度较高,使得大部分人认为࿱…...

正则表达式 —— Awk
Awk awk:文本三剑客之一,是功能最强大的文本工具 awk也是按行来进行操作,对行操作完之后,可以根据指定命令来对行取列 awk的分隔符,默认分隔符是空格或tab键,多个空格会压缩成一个 awk的用法 awk的格式…...

国芯新作 | 四核Cortex-A53@1.4GHz,仅168元起?含税?哇!!!
创龙科技SOM-TLT507是一款基于全志科技T507-H处理器设计的4核ARM Cortex-A53全国产工业核心板,主频高达1.416GHz。核心板CPU、ROM、RAM、电源、晶振等所有元器件均采用国产工业级方案,国产化率100%。 核心板通过邮票孔连接方式引出MIPI CSI、HDMI OUT、…...
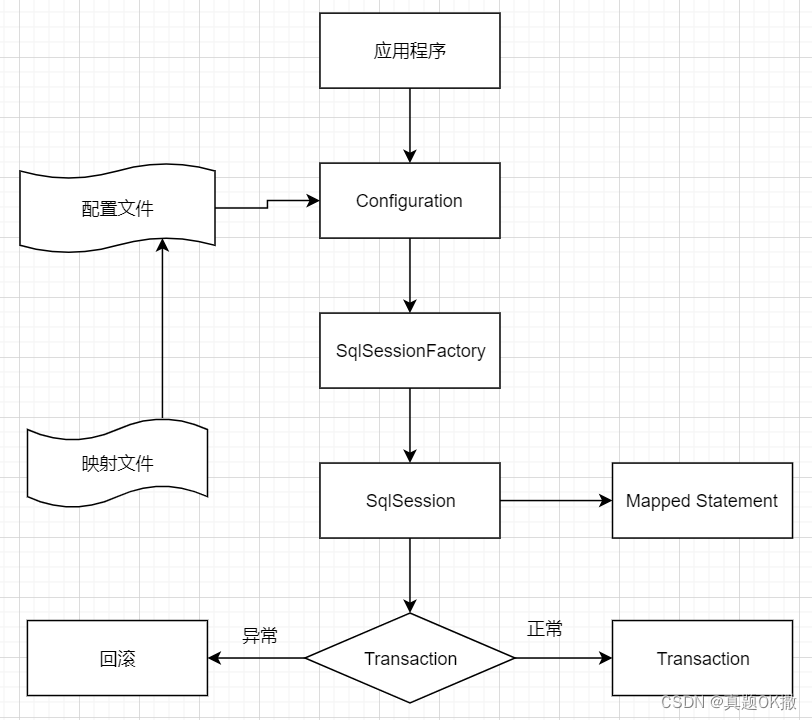
【MyBatis】 框架原理
目录 10.3【MyBatis】 框架原理 10.3.1 【MyBatis】 整体架构 10.3.2 【MyBatis】 运行原理 10.4 【MyBatis】 核心组件的生命周期 10.4.1 SqlSessionFactoryBuilder 10.4.2 SqlSessionFactory 10.4.3 SqlSession 10.4.4 Mapper Instances 与 Hibernate 框架相比&#…...

三、线性工作流
再生产的各个环节,正确使用gamma编码及gamma解码,使得最终得到的颜色数据与最初输入的物理数据一致。如果使用gamma空间的贴图,在传给着色器前需要从gamma空间转到线性空间。 如果不在线性空间下进行渲染,会产生的问题:…...

2023华数杯数学建模A题思路 - 隔热材料的结构优化控制研究
# 1 赛题 A 题 隔热材料的结构优化控制研究 新型隔热材料 A 具有优良的隔热特性,在航天、军工、石化、建筑、交通等 高科技领域中有着广泛的应用。 目前,由单根隔热材料 A 纤维编织成的织物,其热导率可以直接测出;但是 单根隔热…...
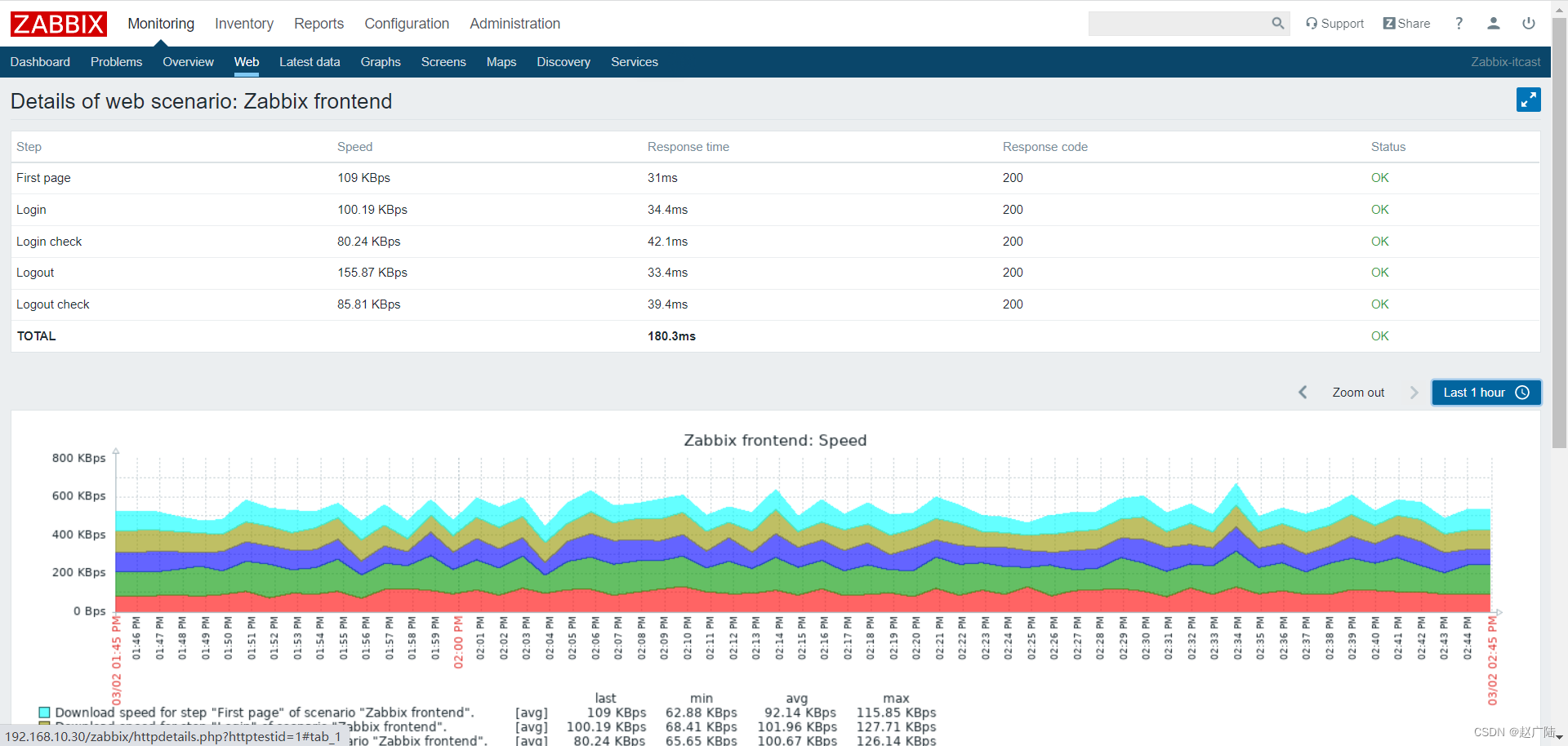
Zabbix分布式监控Web监控
目录 1 概述2 配置 Web 场景2.1 配置步骤2.2 显示 3 Web 场景步骤3.1 创建新的 Web 场景。3.2 定义场景的步骤3.3 保存配置完成的Web 监控场景。 4 Zabbix-Get的使用 1 概述 您可以使用 Zabbix 对多个网站进行可用性方面监控: 要使用 Web 监控,您需要定…...
PHP从入门到精通—PHP开发入门-PHP概述、PHP开发环境搭建、PHP开发环境搭建、第一个PHP程序、PHP开发流程
每开始学习一门语言,都要了解这门语言和进行开发环境的搭建。同样,学生开始PHP学习之前,首先要了解这门语言的历史、语言优势等内容以及了解开发环境的搭建。 PHP概述 认识PHP PHP最初是由Rasmus Lerdorf于1994年为了维护个人网页而编写的一…...

【LeetCode-中等】722. 删除注释
题目链接 722. 删除注释 标签 字符串 步骤 Step1. 先将source合并为一个字符串进行处理,中间补上’\n’,方便后续确定注释开始、结束位置。 string combined; for (auto str : source) {combined str "\n"; }Step2. 定义数组 toDel&am…...

rust里如何判断字符串是否相等呢?
在 Rust 中,有几种方法可以判断字符串是否相等。下面是其中几种常见的方法: 使用 运算符:可以直接使用 运算符比较两个字符串是否相等。例如: fn main() {let str1 "hello";let str2 "world";if str1 …...

python基本知识学习
一、输出语句 在控制台输出Hello,World! print("Hello,World!") 二、注释 单行注释:以#开头 # print("你好") 多行注释: 选中要注释的代码Ctrl/三单引号三双引号 # print("你好") # a1 # a2 print("Hello,World!&…...
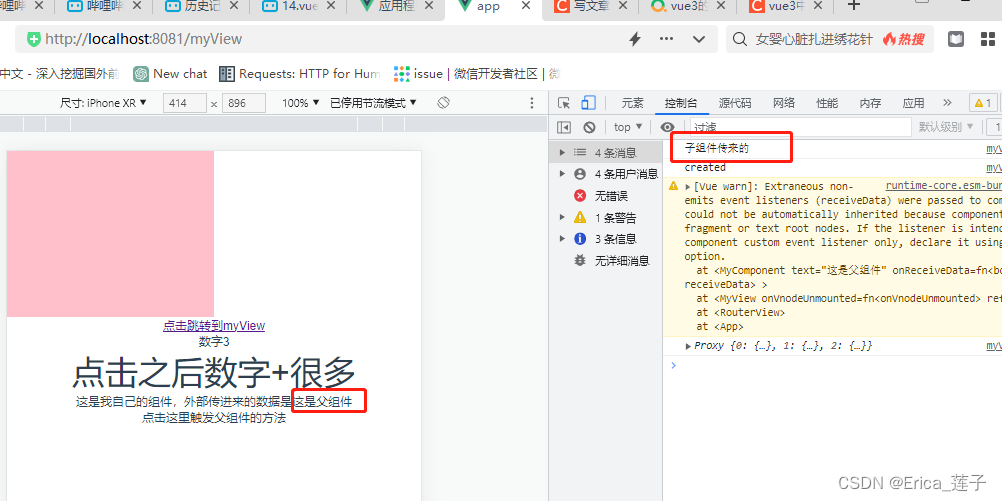
vue3和typescript_组件
1 components下新建myComponent.vue 2 页面中引入组件,传入值,并且绑定事件函数。 3...

Qt+联想电脑管家
1.自定义按钮类 效果: (1)仅当未选中,未悬浮时 (2)其他三种情况,均如图 #ifndef BTN_H #define BTN_H#include <QPushButton> class btn : public QPushButton {Q_OBJECT public:btn(QWidget * parent nullptr);void set_normal_icon(…...
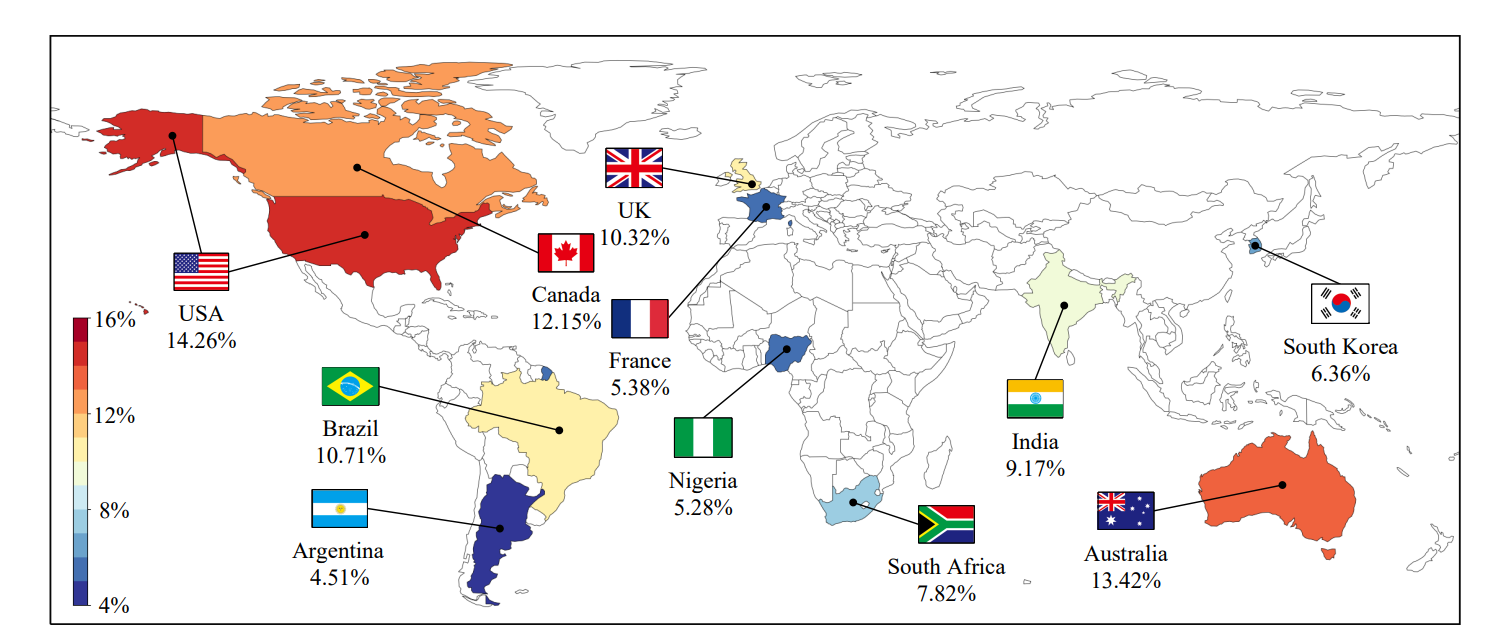
论文阅读-BotPercent: Estimating Twitter Bot Populations from Groups to Crowds
目录 摘要 引言 方法 数据集 BotPercent架构 实验结果 活跃用户中的Bot数量 Bot Population among Comment Sections Bot Participation in Content Moderation Votes Bot Population in Different Countries’ Politics 论文链接:https://arxiv.org/pdf/23…...
用于永磁同步电机驱动器的自适应SDRE非线性无传感器速度控制(MatlabSimulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台免费搭建 qt
Java版知识付费源码 Spring CloudSpring BootMybatisuniapp前后端分离实现知识付费平台 提供职业教育、企业培训、知识付费系统搭建服务。系统功能包含:录播课、直播课、题库、营销、公司组织架构、员工入职培训等。 提供私有化部署,免费售…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
