LA@行列式性质
文章目录
- 行列式性质🎈
- 转置不变性质
- 交换性质
- 多重交换@移动(抽出插入)👺
- 因子提取性质
- 拆和性质
- 倍加性质
- 手算行列式的主要方法
- 原理:任何行列式都可以化为三角行列式
行列式性质🎈
- 设行列式 ∣ A ∣ = d e t ( a i j ) |A|=\mathrm{det}(a_{ij}) ∣A∣=det(aij),行列式性质主要有5条
转置不变性质
-
行列式与它的转置行列式相等
-
或说经过转置,行列式的值不变(方阵 A A A转置前后取行列式的值相等)
-
∣ A T ∣ = ∣ A ∣ |A^T|=|A| ∣AT∣=∣A∣
-
n n n阶方阵 B = A T B=A^T B=AT的内容构成: b i j = a j i b_{ij}=a_{ji} bij=aji, i , j = 1 , 2 , ⋯ , n i,j=1,2,\cdots,n i,j=1,2,⋯,n
-
-
行列式的行性质和列性质是等同的
- 假设方阵 A , B A,B A,B满足: A A A= B T B^T BT,由于转置不改变行列式的值可知,可以通过研究转置矩阵来代替被转置矩阵,从而行性质和列性质就相互等同.
交换性质
- 两行交换位置,行列式值取反 exchange ( ∣ A ∣ , i , j ) = − ∣ A ∣ , i ≠ j \text{exchange}(|A|,i,j)=-|A|,i\neq{j} exchange(∣A∣,i,j)=−∣A∣,i=j
- 如果某个行列式存在有两行相同,那么|A|=0
- 设A存在2行相同的行(分别记为行i,j),这种情况下,将行i,j对调后行列式记为|B|
- 方阵A,B满足关系:B=A,即 ∣ B ∣ = ∣ A ∣ |B|=|A| ∣B∣=∣A∣
- 而上一条性质告诉我们,交换了行列式中的任意2行,结果都要取反; ∣ B ∣ = − ∣ A ∣ |B|=-|A| ∣B∣=−∣A∣
- 综上, ∣ B ∣ = ∣ A ∣ = − ∣ A ∣ |B|=|A|=-|A| ∣B∣=∣A∣=−∣A∣,从而 ∣ A ∣ = 0 |A|=0 ∣A∣=0
- 如果某个行列式存在有两行相同,那么|A|=0
多重交换@移动(抽出插入)👺
-
假设某个操作将行列式的第i行抽出,并插入到第j行的位置( j ≠ i j\neq{i} j=i)
-
这个操作可以通过执行若干次相邻行之间的位置交换实现
-
例如,可以把副对角三角行列式执行若干次行交换得到主对角三角行列式
-
∣ λ n ⋮ λ 2 λ 1 ∣ → ∣ λ 1 λ 2 ⋮ λ n ∣ \begin{vmatrix} {} & {} & {} & {{\lambda _n}} \cr {} & {} & {{\vdots}} & {} \cr {} & {{\lambda _2}} & {} & {} \cr {{\lambda _1}} & {} & {} & {} \cr \end{vmatrix} \to \begin{vmatrix} {{\lambda _1}} & {} & {} & {} \cr {} & {{\lambda _2}} & {} & {} \cr {} & {} & {{\vdots}} & {} \cr {} & {} & {} & {{\lambda_n}} \cr \end{vmatrix} λ1λ2⋮λn → λ1λ2⋮λn
-
将第 n n n行和前 n − 1 n-1 n−1行依次交换位置(第n行逐次上升,执行 n − 1 n-1 n−1次交换后变成第一行,原先其他所有行的行号减1),此时的行列式记为 ∣ A 1 ∣ |A_1| ∣A1∣
- ∣ λ 1 λ n ⋮ λ 2 ∣ \begin{vmatrix} {{\lambda _1}} & {} & {} & {} \cr {} & {} & {} & {{\lambda _n}} \cr {} & {} & {{\vdots}} & {} \cr {} & {{\lambda _2}} & {} & {} \cr \end{vmatrix} λ1λ2⋮λn
-
操作对象变为 A 1 A_1 A1,将 A 1 A_1 A1的最后一行( λ 2 \lambda_2 λ2)通过逐行交换,使其行号变为2,得到 ∣ A 2 ∣ |A_2| ∣A2∣行行列式
-
反复操作( n − 1 n-1 n−1)次,最后得到的主对角线三角行列式为 ∣ A n − 1 ∣ |A_{n-1}| ∣An−1∣,简记为 ∣ A ′ ∣ |A'| ∣A′∣
- n − 1 n-1 n−1次:对于 n , n − 1 , ⋯ , 2 , 1 n,n-1,\cdots,2,1 n,n−1,⋯,2,1n个逆序的数,需要排序n-1次才能从逆序变为正序
- 注意n个数中的n-1个数如果都处在正序结果的正确位置上,那么剩下一个必然也处在正确位置上,所以排序n-1次而不是n次(冒泡排序)
-
∣ A ′ ∣ = ( − 1 ) ∑ i = 1 n − 1 i ∣ A ∣ = ( − 1 ) 1 2 n ( n − 1 ) ∣ A ∣ |A'|=(-1)^{\sum_{i=1}^{n-1}i}|A|=(-1)^{\frac{1}{2}n(n-1)}|A| ∣A′∣=(−1)∑i=1n−1i∣A∣=(−1)21n(n−1)∣A∣
-
因子提取性质
-
行列式的某行(记为第i行)中的每个元素具有公因子k,则k可以提取到行列式之外作为行列式因子
-
∣ ⋮ ⋮ ⋯ ⋮ k a i 1 k a i 2 ⋯ k a i n ⋮ ⋮ ⋯ ⋮ ∣ = k ∣ ⋮ ⋮ ⋯ ⋮ a i 1 a i 2 ⋯ a i n ⋮ ⋮ ⋯ ⋮ ∣ \begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ ka_{i1}& ka_{i2}& \cdots & ka_{in} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix} =k\begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ a_{i1}& a_{i2}& \cdots & a_{in} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix} ⋮kai1⋮⋮kai2⋮⋯⋯⋯⋮kain⋮ =k ⋮ai1⋮⋮ai2⋮⋯⋯⋯⋮ain⋮
-
某行的元素全为0,则行列式 ∣ A ∣ = 0 |A|=0 ∣A∣=0
-
某两行成比例关系,那么 ∣ A ∣ = 0 |A|=0 ∣A∣=0
- 因为根据公因子提取性质,假设成比例的两行的比例系数为k,那么提取k后,行列式内出现相同的2行,由上述性质可知,行列式的值为0
-
拆和性质
-
如果行列式的第i行每个元素拆分为两个元素之和
-
a i , j = b i , j + c i , j a_{i,j}=b_{i,j}+c_{i,j} ai,j=bi,j+ci,j
-
则行列式|A|可以拆成两个行列式之和
- ∣ A ∣ = ∣ A b ∣ + ∣ A c ∣ |A|=|A_{b}|+|A_{c}| ∣A∣=∣Ab∣+∣Ac∣
- ∣ A b ∣ 和 ∣ A c ∣ |A_b|和|A_c| ∣Ab∣和∣Ac∣分别表示|A|的第i行被替换为行b和行c后的行列式
-
∣ a 11 + b 11 a 12 + b 12 ⋯ a 1 n + b 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ + ∣ b 11 b 12 ⋯ b 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ \begin{vmatrix} a_{11}+b_{11}& a_{12}+b_{12}& \cdots & a_{1n}+b_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}& a_{n2}& \cdots & a_{nn} \end{vmatrix} =\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}& a_{n2}& \cdots & a_{nn} \end{vmatrix} +\begin{vmatrix} b_{11}& b_{12}& \cdots & b_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}& a_{n2}& \cdots & a_{nn} \end{vmatrix} a11+b11a21⋮an1a12+b12a22⋮an2⋯⋯⋱⋯a1n+b1na2n⋮ann = a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann + b11a21⋮an1b12a22⋮an2⋯⋯⋱⋯b1na2n⋮ann
-
倍加性质
-
把第i行的k倍加到第j行列式,行列式的值不变
-
i ≠ j i\neq{j} i=j
-
k ∈ R k\in{R} k∈R
-
∣ ⋮ ⋮ ⋯ ⋮ a j 1 + k a i 1 a j 2 + k a i 2 a j n + k a i n ⋮ ⋮ ⋯ ⋮ ∣ = ∣ ⋮ ⋮ ⋯ ⋮ a j 1 a j 2 a j n ⋮ ⋮ ⋯ ⋮ ∣ , ( i ≠ j ) \begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ a_{j1}+ka_{i1}& a_{j2}+ka_{i2}& & a_{jn}+ka_{in} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix} =\begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ a_{j1} & a_{j2} & & a_{jn} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix},(i\neq{j}) ⋮aj1+kai1⋮⋮aj2+kai2⋮⋯⋯⋮ajn+kain⋮ = ⋮aj1⋮⋮aj2⋮⋯⋯⋮ajn⋮ ,(i=j)
-
-
因为,根据上一条性质:
-
∣ ⋮ ⋮ ⋯ ⋮ a i 1 a i 2 a i n ⋮ ⋮ ⋯ ⋮ a j 1 + k a i 1 a j 2 + k a i 2 a j n + k a i n ⋮ ⋮ ⋯ ⋮ ∣ = ∣ ⋮ ⋮ ⋯ ⋮ a i 1 a i 2 a i n ⋮ ⋮ ⋯ ⋮ a j 1 a j 2 a j n ⋮ ⋮ ⋯ ⋮ ∣ + ∣ ⋮ ⋮ ⋯ ⋮ a i 1 a i 2 a i n ⋮ ⋮ ⋯ ⋮ k a i 1 k a i 2 k a i n ⋮ ⋮ ⋯ ⋮ ∣ = ∣ A ∣ + 0 = ∣ A ∣ \\ \begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ a_{i1}& a_{i2}& & a_{in} \\ \vdots & \vdots & \cdots & \vdots\\ a_{j1}+ka_{i1}& a_{j2}+ka_{i2}& & a_{jn}+ka_{in} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix}\\ =\begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ a_{i1}& a_{i2}& & a_{in} \\ \vdots & \vdots & \cdots & \vdots\\ a_{j1}& a_{j2}& & a_{jn} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix} +\begin{vmatrix} \vdots & \vdots & \cdots & \vdots\\ a_{i1}& a_{i2}& & a_{in} \\ \vdots & \vdots & \cdots & \vdots\\ ka_{i1}& ka_{i2}& & ka_{in} \\ \vdots & \vdots & \cdots & \vdots \\ \end{vmatrix} \\ =|A|+0=|A| ⋮ai1⋮aj1+kai1⋮⋮ai2⋮aj2+kai2⋮⋯⋯⋯⋮ain⋮ajn+kain⋮ = ⋮ai1⋮aj1⋮⋮ai2⋮aj2⋮⋯⋯⋯⋮ain⋮ajn⋮ + ⋮ai1⋮kai1⋮⋮ai2⋮kai2⋮⋯⋯⋯⋮ain⋮kain⋮ =∣A∣+0=∣A∣
-
上述性质对于列同样成立🎈
-
用上述性质化简计算行列式时,可以行列混用
-
但是在矩阵(方阵)初等变换中有类似的操作中,是模拟线性方程组高斯消元法的操作
-
如果方程组E1: A x = b A\boldsymbol{x}=b Ax=b的某两个变量 x i , x j x_i,x_j xi,xj位置做交换(连同他们的系数一起),得到的方程组记为E2: A ′ x ′ = b ′ A'\boldsymbol{x'}=b' A′x′=b′,与变换前的方程组是同解的(但是 x i , x j x_i,x_j xi,xj相应的对调)
-
A x = b { ⋯ + a 1 i x i + ⋯ + a 1 j x j + ⋯ = b 1 , ⋯ + a 2 i x i + ⋯ + a 2 j x j + ⋯ = b 2 , ⋮ ⋯ + a n i x i + ⋯ + a n j x j + ⋯ = b n A\boldsymbol{x}=b \\ \left \{ \begin{aligned}{} \cdots+a_{1i} x_{i}+\cdots+a_{1j} x_{j}+\cdots&=b_{1}, \\ \cdots+a_{2i}x_{i}+\cdots+a_{2j} x_{j}+\cdots&=b_{2}, \\ &\vdots\\ \cdots+a_{ni} x_{i}+\cdots+a_{nj} x_{j}+\cdots&=b_{n} \end{aligned} \right. Ax=b⎩ ⎨ ⎧⋯+a1ixi+⋯+a1jxj+⋯⋯+a2ixi+⋯+a2jxj+⋯⋯+anixi+⋯+anjxj+⋯=b1,=b2,⋮=bn
-
{ ⋯ + a 1 j x j + ⋯ + a 1 i x i + ⋯ = b 1 , ⋯ + a 2 j x j + ⋯ + a 2 i x i + ⋯ = b 2 , ⋮ ⋯ + a n j x j + ⋯ + a n i x i + ⋯ = b n A ′ x ′ = b \\ \left \{ \begin{aligned}{} \cdots+a_{1j} x_{j}+\cdots+a_{1 i} x_{i}+\cdots&=b_{1}, \\ \cdots+a_{2j}x_{j}+\cdots+a_{2 i} x_{i}+\cdots&=b_{2}, \\ &\vdots\\ \cdots+a_{nj} x_{j}+\cdots+a_{n i} x_{i}+\cdots&=b_{n} \end{aligned} \right. \\ A'\boldsymbol{x'}=b ⎩ ⎨ ⎧⋯+a1jxj+⋯+a1ixi+⋯⋯+a2jxj+⋯+a2ixi+⋯⋯+anjxj+⋯+anixi+⋯=b1,=b2,⋮=bnA′x′=b
-
上述两个方程组的等价性基于加法交换律
-
从集合的角度来讲 x , x ′ \boldsymbol{x},\boldsymbol{x'} x,x′中的元素构成的集合是等价的( s e t ( x ) = s e t ( x ′ ) set(\boldsymbol{x})=set(\boldsymbol{x'}) set(x)=set(x′),只是顺序上有所不同 x ≠ x ′ \boldsymbol{x}\neq{\boldsymbol{x'}} x=x′
-
-
但是执行倍乘和倍加操作通常会导致方程组的解发生变化,
-
如果系数矩阵的某两列发生交换
-
-
例如,可以先将某两列交换,这可能使得行列式很容易化为上三角行列式
- 将普通行列式等值变形为上三角行列式,往往使得首行的元素尽可能小,再逐列进行化0
- 当第一列符合上三角行列式后,开始处理第二列,此时可以看做n-1阶的,右下角的行列式
- 情况转化为了上一种情况,类似的手法
- 也可通过按行/列展开降维
- 将普通行列式等值变形为上三角行列式,往往使得首行的元素尽可能小,再逐列进行化0
手算行列式的主要方法
原理:任何行列式都可以化为三角行列式
-
∣ A ∣ n = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ |A|_{n}= \begin{vmatrix} a_{11}& a_{12}& \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}& a_{n2}& \cdots & a_{nn} \end{vmatrix} ∣A∣n= a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann
-
以下三角为例
-
∣ A ∣ → ∣ a 11 ′ a 21 ′ a 22 ′ ⋮ ⋮ ⋱ a n 1 ′ a n 2 ′ ⋯ a n n ′ ∣ |A|\to \begin{vmatrix} a_{11}'& & & \\ a_{21}'& a_{22}'& & \\ \vdots & \vdots & \ddots & \\ a_{n1}'& a_{n2}'& \cdots & a_{nn}' \end{vmatrix} ∣A∣→ a11′a21′⋮an1′a22′⋮an2′⋱⋯ann′
-
∣ A ∣ = ∏ i = 1 n a i i ′ |A|=\prod_{i=1}^{n}a_{ii}' ∣A∣=∏i=1naii′
-
-
这个方法是计算行列式的重要方法,通常手算行列式就是采用这个方法👺
-
假设n阶行列式 ∣ A ∣ |A| ∣A∣的最后一行的最后一个元素( a n n a_{nn} ann)是非0元素
- 如果不是,那么可以通过行调整把 a i n , i = 1 , 2 , ⋯ , n a_{in},i=1,2,\cdots,n ain,i=1,2,⋯,n中满足 a i n ≠ 0 a_{in}\neq0 ain=0的任意一行调整到最后一行,使得 a n n ≠ 0 a_{nn}\neq{0} ann=0
- 执行 r i − a i n a n n r n \huge{r_{i}-\frac{a_{in}}{a_{nn}}r_n} ri−annainrn,将各行的结果记为 r i ′ r_i' ri′,此时 r i ′ r_i' ri′的最后一个元素 a i n ′ a_{in}' ain′= a i n − a i n a n n a n n = 0 a_{in}-\frac{a_{in}}{a_{nn}}a_{nn}=0 ain−annainann=0, i = 1 , 2 , ⋯ , n − 1 i=1,2,\cdots,n-1 i=1,2,⋯,n−1
- 即 a 1 , n , ⋯ , a n − 1 , n a_{1,n},\cdots,a_{n-1,n} a1,n,⋯,an−1,n全为0( a n n a_{nn} ann正上方的元素全为0)
- 如果 a 1 , n , ⋯ , a n − 1 , n a_{1,n},\cdots,a_{n-1,n} a1,n,⋯,an−1,n本身就全为0,那么更简单,直接处理前一列(并且这种情况下, ∣ A ∣ = 0 |A|=0 ∣A∣=0)
- 如果不是,那么可以通过行调整把 a i n , i = 1 , 2 , ⋯ , n a_{in},i=1,2,\cdots,n ain,i=1,2,⋯,n中满足 a i n ≠ 0 a_{in}\neq0 ain=0的任意一行调整到最后一行,使得 a n n ≠ 0 a_{nn}\neq{0} ann=0
-
类似的,对于行列式的 1 , ⋯ , n − 1 1,\cdots,n-1 1,⋯,n−1行和列构成的 n − 1 n-1 n−1阶行列式( ∣ A ∣ |A| ∣A∣的余子式 A n n A_{nn} Ann)可以执行类似的行变换,使得
- a 1 , n − 1 , ⋯ , a n − 2 , n − 1 a_{1,n-1},\cdots,a_{n-2,n-1} a1,n−1,⋯,an−2,n−1全为0( a n − 1 , n − 1 a_{n-1,n-1} an−1,n−1正上方的元素全为0)
-
不断执行 r i + a i p a p p r j r_i+\frac{a_{ip}}{a_{pp}}r_j ri+appaiprj,( i = 1 , 2 , ⋯ , p − 1 i=1,2,\cdots,p-1 i=1,2,⋯,p−1; p = n , n − 1 , ⋯ , 2 p=n,n-1,\cdots,2 p=n,n−1,⋯,2),就能够使得 ∣ A ∣ |A| ∣A∣转换为下三角行列式
-
Note:上述操作只涉及到行倍增就可以达到化一般行列式为三角行列式的目的,类似的仅执行列倍增也可以化为三角行列式
相关文章:

LA@行列式性质
文章目录 行列式性质🎈转置不变性质交换性质多重交换移动(抽出插入)👺 因子提取性质拆和性质倍加性质 手算行列式的主要方法原理:任何行列式都可以化为三角行列式 行列式性质🎈 设行列式 ∣ A ∣ d e t ( a i j ) |A|\mathrm{det}(a_{ij}) …...
【java安全】原生反序列化利用链JDK7u21
文章目录 【java安全】原生反序列化利用链JDK7u21前言原理equalsImpl()如何调用equalsImpl()?HashSet通过反序列化间接执行equals()方法如何使hash相等? 思路整理POCGadget为什么在HashSet#add()前要将HashMap的value设为其他值? 【java安全】…...

[SQL智慧航行者] - SQL刷题规划
前言: 不知不觉, 慢慢的把一些基础知识整理到了现在. SQL挖掘机系列可能就要到此结束了. 目前是规划把这部分SQL练习部分放到SQL刷题的专栏, 就不放到SQL专栏了. 因为后续如果接触更多的知识点和题目也好分类. 请大家如果关注的话, 想看SQL知识点 --> SQL专栏; 想看SQL刷…...

概率论与数理统计:第一章:随机事件及其概率
文章目录 概率论Ch1. 随机事件及其概率1.基本概念(1)随机试验、随机事件、样本空间(2)事件的关系和运算①定义:互斥(互不相容)、对立②运算法则:德摩根率 (3)概率的定义(4)概率的性质(5)概率计算排列组合 2.等可能概型1.古典概型 (离散)2.几何概型 (连续…...

elementUi重置Select选择器样式、option、deep、vue3、plus
文章目录 前言select选框样式(element-plus)option选项面板样式(element-plus) 前言 样式标签属性为<style scoped lang"scss"></style> select选框样式(element-plus) // 设置选择框的背景样式 ::v-deep .el-input__wrapper {background: transparent;b…...
jar命令的安装与使用
场景: 项目中经常遇到使用WinR软件替换jar包中的文件,有时候存在WinRAR解压替换时提示没有权限,此时winRAR不能用还有有什么方法替换jar包中的文件。 方法: 使用jar命令进行修改替换 问题: 执行jar命令报错jar 不…...

windows系统多线程多进程下应用函数CloseHandle的一些细节
Windows CloseHandle()函数调用之后,对应的内核对象的句柄计数器减去1。如果此内核对象的句柄的计数器计数变为0,系统会回收此内核对象。所以,如果创建了内核对象(例如可调用了CreateThread创建一个线程内核对象。此对象创建成功后此线程内核…...

微服务——elasticsearch
初识ES——什么是elasticsearch elasticsearch的发展 初识ES——正向索引和倒排索引 初识ES——es与mysql的概念对比 类比到mysql中是表结构约束 概念对比 初始ES——安装es和kibana 1.部署单点es 1.1创建网络 要安装es容器和kibana容器并让他们之间相连,这里…...
paddlenlp:社交网络中多模态虚假媒体内容核查
初赛之环境配置篇 一、背景二、任务三、数据集1、初赛阶段2、评分标准 四、环境操作五、写在最后 一、背景 随着新媒体时代信息媒介的多元化发展,各种内容大量活跃在媒体内中,与此同时各类虚假信息也充斥着社交媒体,影响着公众的判断和决策。…...

Centos系统有哪些特点呢
CentOS 是一个基于 Red Hat Enterprise Linux (RHEL) 的免费的开源操作系统,由 CentOS 项目维护。CentOS 项目是一个社区驱动的项目,旨在为用户提供一个稳定的、可扩展的 Linux 发行版。 CentOS 系统具有以下特点: 稳定性:CentOS 系统非常稳定,即使是在高负载的环境下也是如此…...
一文学会git常用命令和使用指南
文章目录 0. 前言1.分支分类和管理1. 分支分类规范:2. 最佳实践3. 分支命名规范示例:4. 分支管理方法: 2. commit 注释规范1. 提交注释结构:2. 提交注释的准则: 3. git 常用命令1. git pull 核心用法2. git push 命令1…...
[PyTorch][chapter 46][LSTM -1]
前言: 长短期记忆网络(LSTM,Long Short-Term Memory)是一种时间循环神经网络,是为了解决一般的RNN(循环神经网络)存在的长期依赖问题而专门设计出来的。 目录: 背景简介 LSTM C…...
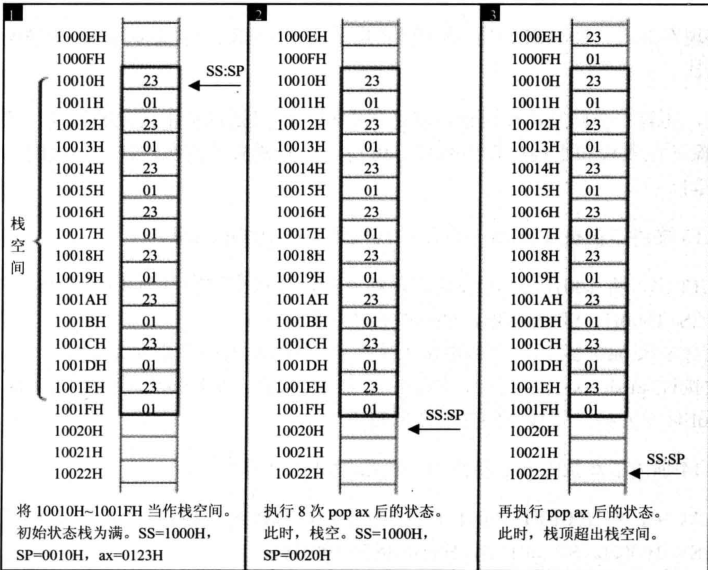
寄存器详解(二)
目录 内存中字的存储 示例: 数据段寄存器DS与[address] 字的传送 数据段简介 CPU提供的栈机制 栈段寄存器SS和栈顶指针寄存器SP PUSH AX指令的完整描述 示例图 POP AX指令的完整描述 示例图 栈顶超界问题 示例一: 示例二: 内存中字…...

Java AIO
在Java中,AIO代表异步I/O(Asynchronous I/O),它是Java NIO的一个扩展,提供了更高级别的异步I/O操作。AIO允许应用程序执行非阻塞I/O操作,而无需使用Selector和手动轮询事件的方式。 与传统的NIO和Java NIO…...

java集合总结
1.常见集合 Collection List:有序可重复集合,可直接根据元素的索引来访问 Vector-StackArrayListLinkedList Queue:队列集合 Deque-LinkedList、ArrayDequePriorityQueue Set:无序不可重复集合,只能根据元素本身来访问…...

list交并补差集合
list交并补差集合 工具类依赖 <dependency><groupId>org.apache.commons</groupId><artifactId>commons-lang3</artifactId><version>3.8.1</version> </dependency><dependency><groupId>commons-collections&…...

【微信小程序】父组件修改子组件数据或调用子组件方法
一、使用场景 页面中用到了自定义组件形成父子组件关系,在父组件某个特定时期想要操作子组件中的数据或方法,比如离开页面的时候清空子组件的数据。 二、方法 父组件可以通过this.selectComponent方法获取子组件实例对象,这样就可以直接访…...

frp通过nginx映射multipart/x-mixed-replace; boundary=frame流媒体出外网访问
要通过Nginx访问multipart/x-mixed-replace流媒体协议,并通过FRP进行映射访问,你可以按照以下步骤进行操作: 配置Nginx以支持multipart/x-mixed-replace流媒体协议。你需要编辑Nginx的配置文件(通常是nginx.conf)&…...
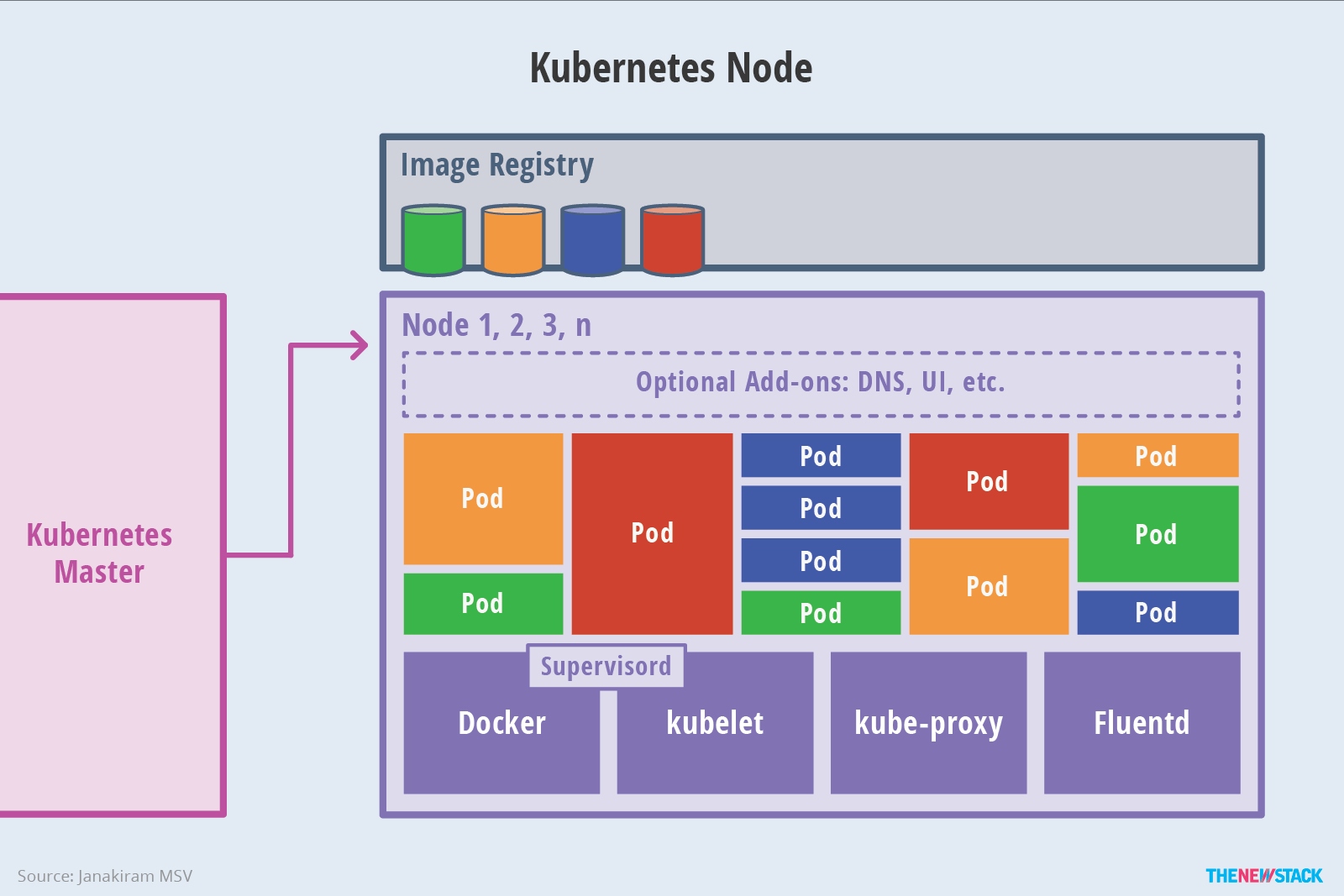
Kubernetes概述
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...

Jmeter教程
目录 安装与配置 一:下载jdk——配置jdk环境变量 二:下载JMeter——配置环境变量 安装与配置 一:下载jdk——配置jdk环境变量 1.新建环境变量变量名:JAVA_HOME变量值:(即JDK的安装路径) 2.编辑Path%J…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
