概率论与数理统计:第一章:随机事件及其概率
文章目录
- 概率论
- Ch1. 随机事件及其概率
- 1.基本概念
- (1)随机试验、随机事件、样本空间
- (2)事件的关系和运算
- ①定义:互斥(互不相容)、对立
- ②运算法则:德摩根率
- (3)概率的定义
- (4)概率的性质
- (5)概率计算
- 排列组合
- 2.等可能概型
- 1.古典概型 (离散)
- 2.几何概型 (连续)
- 3.七大公式
- (1)逆事件概率公式
- (2)加法公式
- (3)减法公式
- (4)条件概率公式
- (5)乘法公式
- (6)全概率公式
- (7)贝叶斯公式 (先验概率)
- 4.独立性
- (1)事件的独立性
- (2)n重伯努利概型 (独立试验序列概型)
概率论


Ch1. 随机事件及其概率
1.基本概念
①古典概型求概率
②几何概型求概率
③七大公式求概率
④独立性
(1)随机试验、随机事件、样本空间
1.随机试验 E

2.随机事件 A、B、C
①必然事件 Ω: P ( Ω ) = 1 P(Ω)=1 P(Ω)=1
②不可能事件 Ø: P ( Ø ) = 0 P(Ø)=0 P(Ø)=0

3.样本空间
①样本点 ω = 基本事件
②样本空间 Ω:样本点的全体组成的集合

(2)事件的关系和运算
①定义:互斥(互不相容)、对立
(一) 关系:包含、相等、相容、(互不相容)互斥、对立
(二) 运算:和(并)、差、积(交)
(一) 事件的关系
1.包含
(1)概念:

(2)性质:
① A ⊂ B A \subset B A⊂B,则 P ( A ) ≤ P ( B ) P(A)≤P(B) P(A)≤P(B)
② A B ⊂ A AB\subset A AB⊂A且 A B ⊂ B AB\subset B AB⊂B,即 P(AB)≤P(A)且P(AB)≤P(B)
(3)若事件C发生必然导致事件A与B同时发生,则A、B、C事件关系为: C ⊂ A B C\subset AB C⊂AB
2.相等

3.相容

4.互不相容(互斥)
(1)定义:
若事件A,B互斥,则
①事件角度:AB=Ø
②概率角度:P(AB)=0
(2)性质:
AB=Ø,则 A ⊂ B ‾ A\subset \overline B A⊂B, P ( A ) ≤ P ( B ‾ ) P(A)≤P(\overline B) P(A)≤P(B)

5.对立:对立事件、逆事件
① A B = Ø AB=Ø AB=Ø 且 A ∪ B = Ω A∪B=Ω A∪B=Ω (即 A ˉ \bar{A} Aˉ=B)
②P(AB)=0 且 P(A)+P(B)=1

(二)事件的运算
1.和(并):A∪B
2.差:$A-B=A∩\overline{B} $

3.积(交):A∩B 或 AB
例题1:12年14.
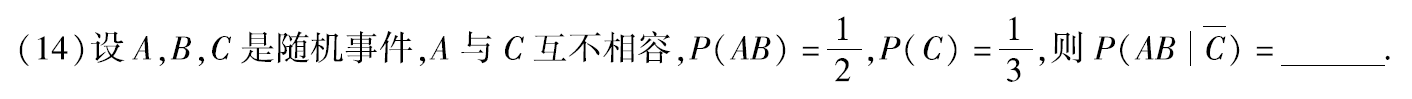
答案:3/4
②运算法则:德摩根率
5.德摩根率(对偶律) 【长杠变短杠,开口换方向】
(1) A ∪ B ‾ = A ‾ ∩ B ‾ = A ‾ B ‾ \overline{A∪B}=\overline{A}∩\overline{B}=\overline{A}\ \overline{B} A∪B=A∩B=A B:A、B均不发生
(2) A B ‾ = A ‾ ∪ B ‾ \overline{AB}=\overline{A}∪\overline{B} AB=A∪B:A、B至少有一个不发生
方法:转化为带并的来看含义
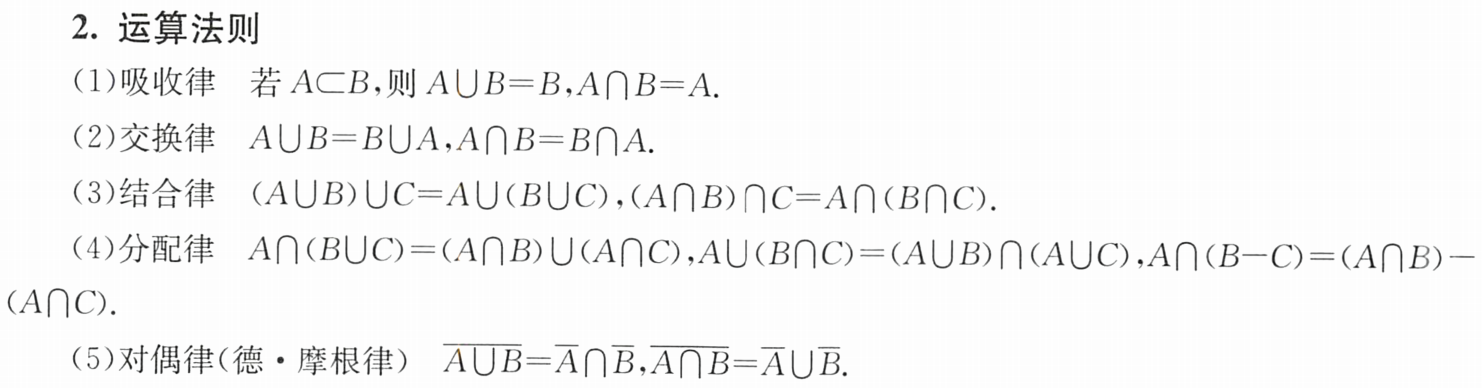
例题1:

分析:
A={甲畅销,乙滞销}=B∩C
A ˉ = B ∩ C ‾ = B ‾ ∪ C ‾ \bar{A}=\overline{B∩C}=\overline{B}∪\overline{C} Aˉ=B∩C=B∪C=甲滞销 或 乙畅销
答案:C
例题2:

法一:推导
法二:画图
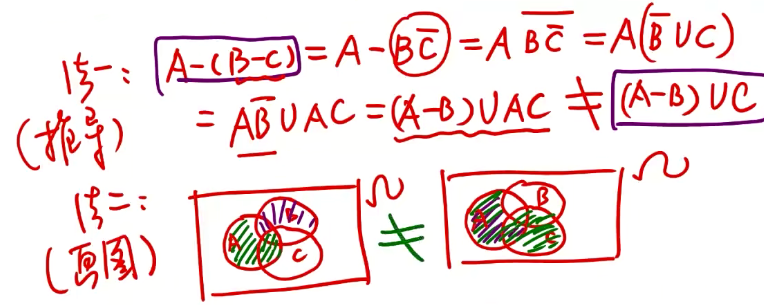
(3)概率的定义
1.用频率去估计概率

2.概率的公理化定义
①非负性: P ( A ) ≥ 0 P(A)≥0 P(A)≥0
②规范性: P ( Ω ) = 1 P(Ω)=1 P(Ω)=1
③可列可加性:任意可列个两两互不相容的事件 A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An,有 P ( A 1 ∪ A 2 ∪ . . . ∪ A n ) = P ( A 1 ) + P ( A 2 ) + . . . + P ( A n ) P(A_1∪A_2∪...∪A_n)=P(A_1)+P(A_2)+...+P(A_n) P(A1∪A2∪...∪An)=P(A1)+P(A2)+...+P(An) 【完备事件组】
(4)概率的性质
(1)有界性:
对任意事件A,有 0 ≤ P ( A ) ≤ 1 0≤P(A)≤1 0≤P(A)≤1。
注:对于几何概型:若P(A)=0,不能断言 A=Ø;若P(A)=1,不能断言 A=Ω;
但反之则对:若A是空集Ø,则P(A)=0;若A是全集Ω,则P(A)=1。即一定有 P ( Ø ) = 0 , P ( Ω ) = 1 P(Ø)=0,P(Ω)=1 P(Ø)=0,P(Ω)=1。
(2)单调性:
对于A,B两个事件,若有 A ⊂ B A\subset B A⊂B,则有:
①P(A)≤P(B)
②P(B-A)=P(B)-P(A)
(5)概率计算
跳转链接
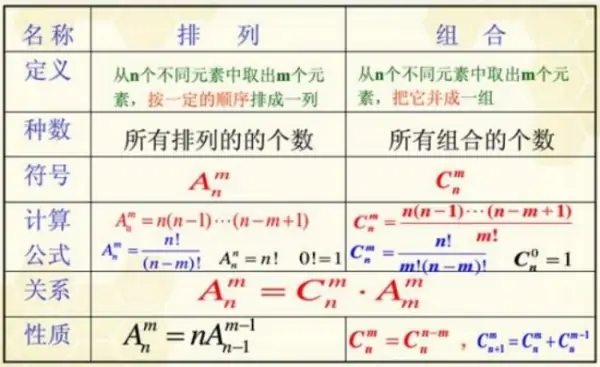
排列组合
| 排列 | 组合 | |
|---|---|---|
| 符号 | A n m A_n^m Anm | C n m C_n^m Cnm |
| 公式 | A n m = n ( n − 1 ) . . . ( n − m − 1 ) A_n^m=n(n-1)...(n-m-1) Anm=n(n−1)...(n−m−1) | C n m = n ( n − 1 ) . . . ( n − m − 1 ) m ! C_n^m=\dfrac{n(n-1)...(n-m-1)}{m!} Cnm=m!n(n−1)...(n−m−1) |
| 关系 | A n m = A_n^m= Anm= | C n m ⋅ m ! C_n^m·m! Cnm⋅m! |
2.等可能概型
1.古典概型 (离散)
古典概型(离散),研究工具:①排列组合 ②加法原理、乘法原理 ③直接数数

求法:
(1)直接用定义求概率: P ( A ) = k n P(A)=\dfrac{k}{n} P(A)=nk
(2)随机分配:m个可辩质点,放到n个盒子中
①每个盒子可以放任意多个质点:有 n m n^m nm 种放法
②每个盒子只能放一个质点:有 A n m = n ( n − 1 ) . . . ( n − m + 1 ) A_n^m=n(n-1)...(n-m+1) Anm=n(n−1)...(n−m+1) 种放法

(3)简单随机抽样
| 含义 | 共有多少种不同的取法 | |
|---|---|---|
| ①先后有放回 | m个球,先后有放回地取n次 | m n m^n mn |
| ②先后无放回 | m个球,先后无放回地取n次 | A m n = m ( m − 1 ) . . . ( m − n + 1 ) A_m^n=m(m-1)...(m-n+1) Amn=m(m−1)...(m−n+1) |
| ③任取(一次性同时拿出) | 从n中一次性取m个球 | C n m C_n^m Cnm |

2.几何概型 (连续)
几何概型(连续),研究工具:几何方法、微积分
P ( A ) = S A 的几何度量 Ω 的几何度量 P(A)=\dfrac{S_A的几何度量}{Ω的几何度量} P(A)=Ω的几何度量SA的几何度量
几何度量:长度、面积、体积

例题1:07年16. 几何概型

分析:
法一:直接观察,使得 x-y绝对值小于0.5

显然,概率应为 3 4 \dfrac{3}{4} 43
法二:随机变量的概率
| 文字语言 | 数学语言 |
|---|---|
| 两个数之差的绝对值 | ∣ X − Y ∣ \lvert X-Y\rvert ∣X−Y∣ |
| 两个数之差的绝对值小于 1 2 \dfrac{1}{2} 21 | ∣ X − Y ∣ < 1 2 \lvert X-Y\rvert<\dfrac{1}{2} ∣X−Y∣<21 |
| 两个数之差的绝对值小于 1 2 \dfrac{1}{2} 21的概率 | P { ∣ X − Y ∣ < 1 2 } P\{\ \lvert X-Y\rvert<\dfrac{1}{2}\ \} P{ ∣X−Y∣<21 } |
则 P { ∣ X − Y ∣ < 1 2 } = P { − 1 2 < X − Y < 1 2 } = P { − 1 2 < Y − X < 1 2 } = P { x − 1 2 < Y < x + 1 2 } P\{|X-Y|<\dfrac{1}{2}\}=P\{-\dfrac{1}{2}<X-Y<\dfrac{1}{2}\}=P\{-\dfrac{1}{2}<Y-X<\dfrac{1}{2}\}=P\{x-\dfrac{1}{2}<Y<x+\dfrac{1}{2}\} P{∣X−Y∣<21}=P{−21<X−Y<21}=P{−21<Y−X<21}=P{x−21<Y<x+21}
即在 0 < x < 1 , 0 < y < 1 0<x<1,0<y<1 0<x<1,0<y<1区域内,落在 y = x + 1 2 y=x+\dfrac{1}{2} y=x+21 和 y = x − 1 2 y=x-\dfrac{1}{2} y=x−21 之间的概率。

答案: 3 4 \dfrac{3}{4} 43
3.七大公式
(1)逆事件概率公式
P ( A ‾ ) = 1 − P ( A ) P(\overline A)=1-P(A) P(A)=1−P(A)
(2)加法公式
1.任意事件
①两事件和的概率: P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) P(A∪B)=P(A)+P(B)-P(AB) P(A∪B)=P(A)+P(B)−P(AB)
②三事件和的概率: P ( A ∪ B ∪ C ) = P ( A ) + P ( B ) + P ( C ) − P ( A B ) − P ( B C ) − P ( A C ) + P ( A B C ) P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) P(A∪B∪C)=P(A)+P(B)+P(C)−P(AB)−P(BC)−P(AC)+P(ABC)
③四事件和的概率: P ( A ∪ B ∪ C ∪ D ) = [ P ( A ) + P ( B ) + P ( C ) + P ( D ) ] − [ P ( A B ) + P ( A C ) + P ( A D ) + P ( B C ) + P ( B D ) + P ( C D ) ] + [ P ( A B C ) + P ( A B D ) + P ( A C D ) + P ( B C D ) ] − P ( A B C D ) P(A∪B∪C∪D)=[P(A)+P(B)+P(C)+P(D)]-[P(AB)+P(AC)+P(AD)+P(BC)+P(BD)+P(CD)]+[P(ABC)+P(ABD)+P(ACD)+P(BCD)]-P(ABCD) P(A∪B∪C∪D)=[P(A)+P(B)+P(C)+P(D)]−[P(AB)+P(AC)+P(AD)+P(BC)+P(BD)+P(CD)]+[P(ABC)+P(ABD)+P(ACD)+P(BCD)]−P(ABCD)
2.两两互不相容事件:
互斥条件下的加法公式,和的概率 = 概率的和

(3)减法公式
P ( A − B ) = P ( A ) − P ( A B ) = P ( A B ‾ ) P(A-B)=P(A)-P(AB)=P(A\overline{B}) P(A−B)=P(A)−P(AB)=P(AB)

(4)条件概率公式
条件概率:A发生条件下,B发生的概率,记为 P ( B ∣ A ) P(B|A) P(B∣A),前提要求P(A)>0 【垂帘听政】
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\dfrac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
注:①条件概率也是概率,概率的性质仍都满足
(5)乘法公式
① P ( A B ) = P ( A ) ⋅ P ( B ∣ A ) P(AB)=P(A)·P(B|A) P(AB)=P(A)⋅P(B∣A)
② P ( A 1 A 2 A 3 ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) P(A_1A_2A_3)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2) P(A1A2A3)=P(A1)P(A2∣A1)P(A3∣A1A2) 【上过台的,到帘子后面】
(6)全概率公式
1.完备事件组:任意两两互斥,概率有可列可加性
2.全概率公式 【全集分解公式,由因导果】
P ( B ) = ∑ i = 1 n P ( B A i ) = P ( B A 1 ) + P ( B A 2 ) + . . . P ( B A n ) = P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) + . . . + P ( A n ) P ( B ∣ A n ) P(B) = \sum\limits_{i=1}^nP(BA_i)=P(BA_1)+P(BA_2)+...P(BA_n)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n) P(B)=i=1∑nP(BAi)=P(BA1)+P(BA2)+...P(BAn)=P(A1)P(B∣A1)+P(A2)P(B∣A2)+...+P(An)P(B∣An) 【谁去干的概率×干成功的概率】
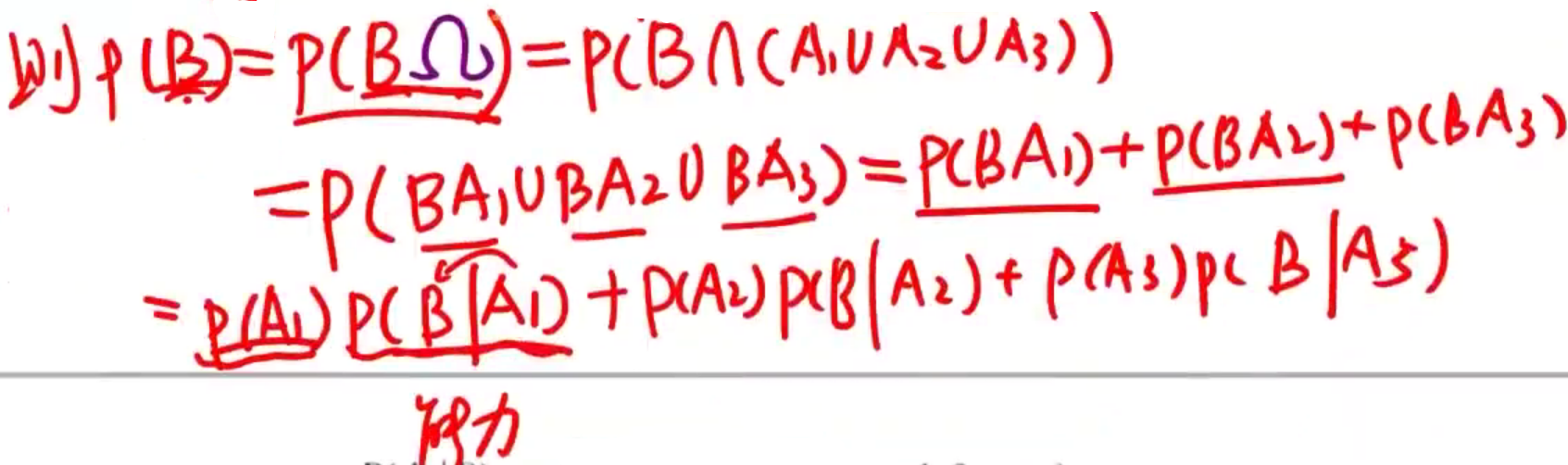
例: P { Y ≤ y } = P { X = 1 } ⋅ P { Y ≤ y ∣ X = 1 } + P { X = 2 } ⋅ P { Y ≤ y ∣ X = 2 } P\{Y≤y\} = P\{X=1\}·P\{Y≤y|X=1\}+ P\{X=2\}·P\{Y≤y|X=2\} P{Y≤y}=P{X=1}⋅P{Y≤y∣X=1}+P{X=2}⋅P{Y≤y∣X=2}
对y的取值进行分类讨论:①y<0 ②0≤y<1 ③1≤y<2 ④y>2
(7)贝叶斯公式 (先验概率)
贝叶斯公式(逆概率公式,执果索因):已知B发生了,求是谁干的?
P ( A k ∣ B ) = P ( B A k ) P ( B ) = P ( A k ) P ( B ∣ A k ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) = 全概率的某一项 全概率公式 P(A_k|B)=\dfrac{P(BA_k)}{P(B)}=\dfrac{P(A_k)P(B|A_k)}{\sum\limits_{i=1}^nP(A_i)P(B|A_i)}=\dfrac{全概率的某一项}{全概率公式} P(Ak∣B)=P(B)P(BAk)=i=1∑nP(Ai)P(B∣Ai)P(Ak)P(B∣Ak)=全概率公式全概率的某一项
在全概率时,每个人干的可能性一般是等可能的。但当事件发生后,每个人干的可能性就发生了变化。
即贝叶斯公式:增加信息,概率的大小可能要修正
例题1:随机事件的概率

分析: 德摩根律(对偶率)
A
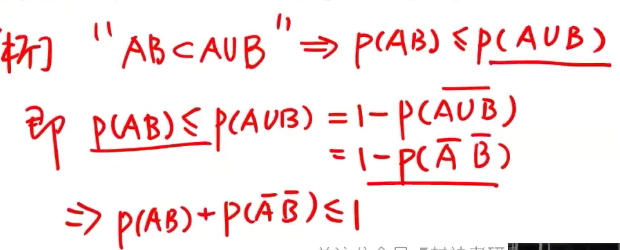
C 包含的性质
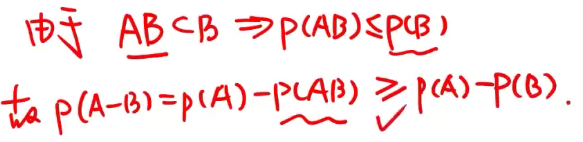
D 逆事件概率公式 + 德摩根律(对偶率)
答案:A
例题2:18年14. 条件概率、事件的独立性
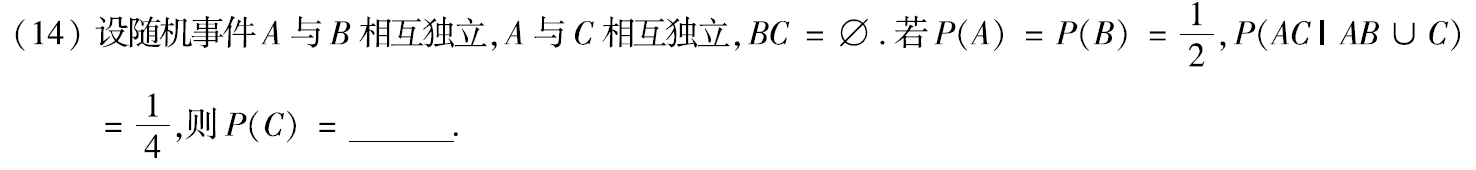
分析:关键是分析出P(AC(AB∪C))=P(AC)
因为BC=Ø,∴P(BC)=0,P(ABC)=0
P ( A C ∣ A B ∪ C ) = P ( A C ( A B ∪ C ) ) P ( A B ∪ C ) = P ( A B C ∪ A C ) ) P ( A B ∪ C ) = P ( A C ) ) P ( A B ) + P ( C ) − P ( A B C ) = P ( A ) P ( C ) ) P ( A ) P ( B ) + P ( C ) = 1 4 P(AC|AB∪C)=\dfrac{P(AC(AB∪C))}{P(AB∪C)}=\dfrac{P(ABC∪AC))}{P(AB∪C)}=\dfrac{P(AC))}{P(AB)+P(C)-P(ABC)}=\dfrac{P(A)P(C))}{P(A)P(B)+P(C)}=\dfrac{1}{4} P(AC∣AB∪C)=P(AB∪C)P(AC(AB∪C))=P(AB∪C)P(ABC∪AC))=P(AB)+P(C)−P(ABC)P(AC))=P(A)P(B)+P(C)P(A)P(C))=41
∴ P ( C ) = 1 4 ∴P(C)=\dfrac{1}{4} ∴P(C)=41

答案: 1 4 \dfrac{1}{4} 41
例题3:15年7. 交与并、加法公式

分析:交的概率大于等于并的概率
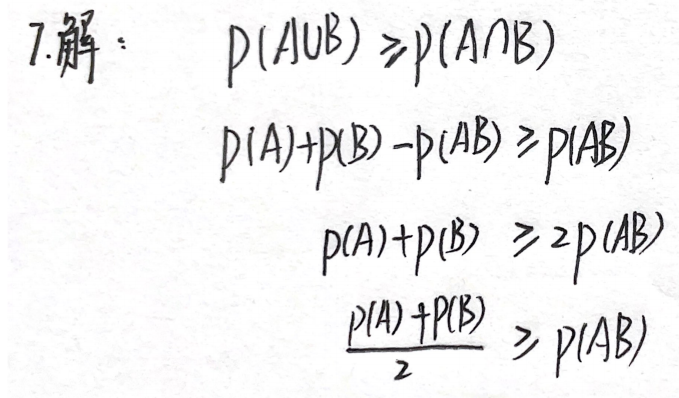
答案:C
例题4:21年16. 全概率公式 + 条件概率

分析:

答案: 1 5 \dfrac{1}{5} 51
例题5:23李林六(三)16.
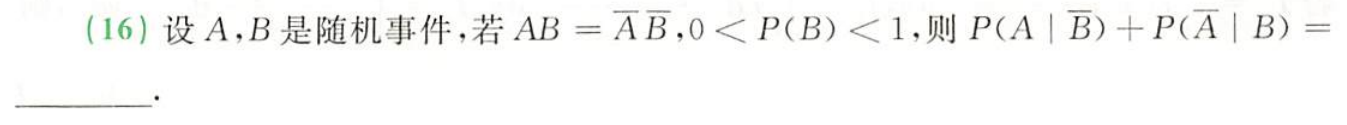
分析:法1:特殊值 法2:正面解

答案:2
例题6:全概率公式

分析:分两次全概率:①抽验样本为正品 ②该箱通过验收

答案:0.887
例题7:贝叶斯公式

分析:

答案: 3 28 \dfrac{3}{28} 283
4.独立性
(1)事件的独立性
(1)数学定义:事件A、B独立 ⇔ P ( A B ) = P ( A ) ⋅ P ( B ) \Leftrightarrow P(AB)=P(A)·P(B) ⇔P(AB)=P(A)⋅P(B)
不可能事件Ø,与任意事件独立
(2)可推得A、B独立条件下的条件概率公式: P ( A ∣ B ) = P ( A ) , P ( B ∣ A ) = P ( B ) P(A|B)=P(A),P(B|A)=P(B) P(A∣B)=P(A),P(B∣A)=P(B) 【描述性定义:结果不受影响 】

(3)n个事件相互独立、n个事件两两独立

例题1:
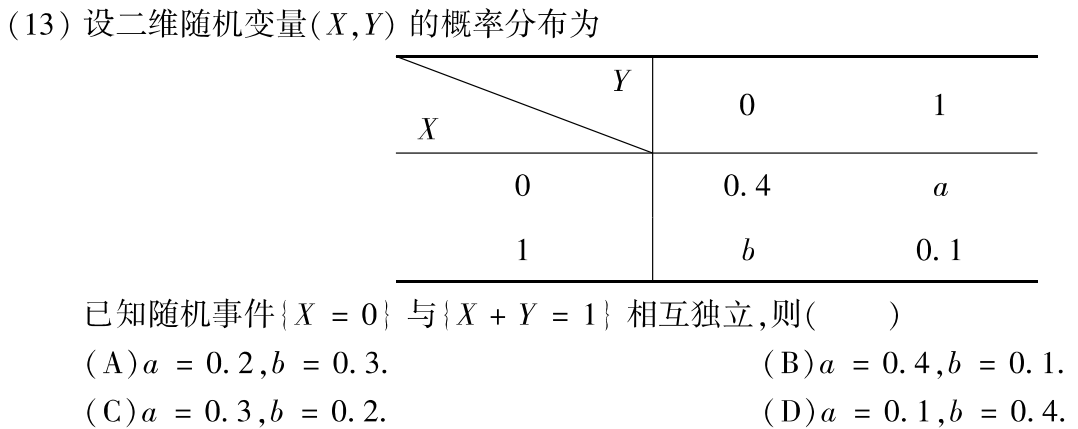
分析:

答案:B
(2)n重伯努利概型 (独立试验序列概型)
相关文章:

概率论与数理统计:第一章:随机事件及其概率
文章目录 概率论Ch1. 随机事件及其概率1.基本概念(1)随机试验、随机事件、样本空间(2)事件的关系和运算①定义:互斥(互不相容)、对立②运算法则:德摩根率 (3)概率的定义(4)概率的性质(5)概率计算排列组合 2.等可能概型1.古典概型 (离散)2.几何概型 (连续…...

elementUi重置Select选择器样式、option、deep、vue3、plus
文章目录 前言select选框样式(element-plus)option选项面板样式(element-plus) 前言 样式标签属性为<style scoped lang"scss"></style> select选框样式(element-plus) // 设置选择框的背景样式 ::v-deep .el-input__wrapper {background: transparent;b…...
jar命令的安装与使用
场景: 项目中经常遇到使用WinR软件替换jar包中的文件,有时候存在WinRAR解压替换时提示没有权限,此时winRAR不能用还有有什么方法替换jar包中的文件。 方法: 使用jar命令进行修改替换 问题: 执行jar命令报错jar 不…...

windows系统多线程多进程下应用函数CloseHandle的一些细节
Windows CloseHandle()函数调用之后,对应的内核对象的句柄计数器减去1。如果此内核对象的句柄的计数器计数变为0,系统会回收此内核对象。所以,如果创建了内核对象(例如可调用了CreateThread创建一个线程内核对象。此对象创建成功后此线程内核…...

微服务——elasticsearch
初识ES——什么是elasticsearch elasticsearch的发展 初识ES——正向索引和倒排索引 初识ES——es与mysql的概念对比 类比到mysql中是表结构约束 概念对比 初始ES——安装es和kibana 1.部署单点es 1.1创建网络 要安装es容器和kibana容器并让他们之间相连,这里…...
paddlenlp:社交网络中多模态虚假媒体内容核查
初赛之环境配置篇 一、背景二、任务三、数据集1、初赛阶段2、评分标准 四、环境操作五、写在最后 一、背景 随着新媒体时代信息媒介的多元化发展,各种内容大量活跃在媒体内中,与此同时各类虚假信息也充斥着社交媒体,影响着公众的判断和决策。…...

Centos系统有哪些特点呢
CentOS 是一个基于 Red Hat Enterprise Linux (RHEL) 的免费的开源操作系统,由 CentOS 项目维护。CentOS 项目是一个社区驱动的项目,旨在为用户提供一个稳定的、可扩展的 Linux 发行版。 CentOS 系统具有以下特点: 稳定性:CentOS 系统非常稳定,即使是在高负载的环境下也是如此…...
一文学会git常用命令和使用指南
文章目录 0. 前言1.分支分类和管理1. 分支分类规范:2. 最佳实践3. 分支命名规范示例:4. 分支管理方法: 2. commit 注释规范1. 提交注释结构:2. 提交注释的准则: 3. git 常用命令1. git pull 核心用法2. git push 命令1…...
[PyTorch][chapter 46][LSTM -1]
前言: 长短期记忆网络(LSTM,Long Short-Term Memory)是一种时间循环神经网络,是为了解决一般的RNN(循环神经网络)存在的长期依赖问题而专门设计出来的。 目录: 背景简介 LSTM C…...
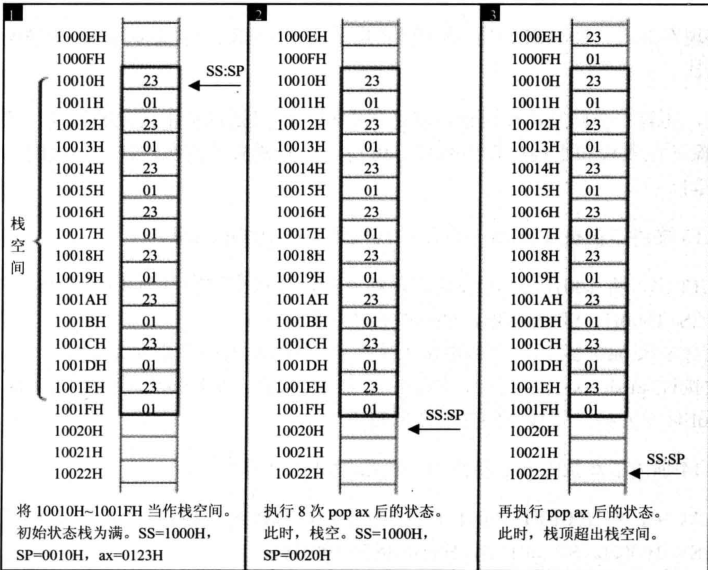
寄存器详解(二)
目录 内存中字的存储 示例: 数据段寄存器DS与[address] 字的传送 数据段简介 CPU提供的栈机制 栈段寄存器SS和栈顶指针寄存器SP PUSH AX指令的完整描述 示例图 POP AX指令的完整描述 示例图 栈顶超界问题 示例一: 示例二: 内存中字…...

Java AIO
在Java中,AIO代表异步I/O(Asynchronous I/O),它是Java NIO的一个扩展,提供了更高级别的异步I/O操作。AIO允许应用程序执行非阻塞I/O操作,而无需使用Selector和手动轮询事件的方式。 与传统的NIO和Java NIO…...

java集合总结
1.常见集合 Collection List:有序可重复集合,可直接根据元素的索引来访问 Vector-StackArrayListLinkedList Queue:队列集合 Deque-LinkedList、ArrayDequePriorityQueue Set:无序不可重复集合,只能根据元素本身来访问…...

list交并补差集合
list交并补差集合 工具类依赖 <dependency><groupId>org.apache.commons</groupId><artifactId>commons-lang3</artifactId><version>3.8.1</version> </dependency><dependency><groupId>commons-collections&…...

【微信小程序】父组件修改子组件数据或调用子组件方法
一、使用场景 页面中用到了自定义组件形成父子组件关系,在父组件某个特定时期想要操作子组件中的数据或方法,比如离开页面的时候清空子组件的数据。 二、方法 父组件可以通过this.selectComponent方法获取子组件实例对象,这样就可以直接访…...

frp通过nginx映射multipart/x-mixed-replace; boundary=frame流媒体出外网访问
要通过Nginx访问multipart/x-mixed-replace流媒体协议,并通过FRP进行映射访问,你可以按照以下步骤进行操作: 配置Nginx以支持multipart/x-mixed-replace流媒体协议。你需要编辑Nginx的配置文件(通常是nginx.conf)&…...
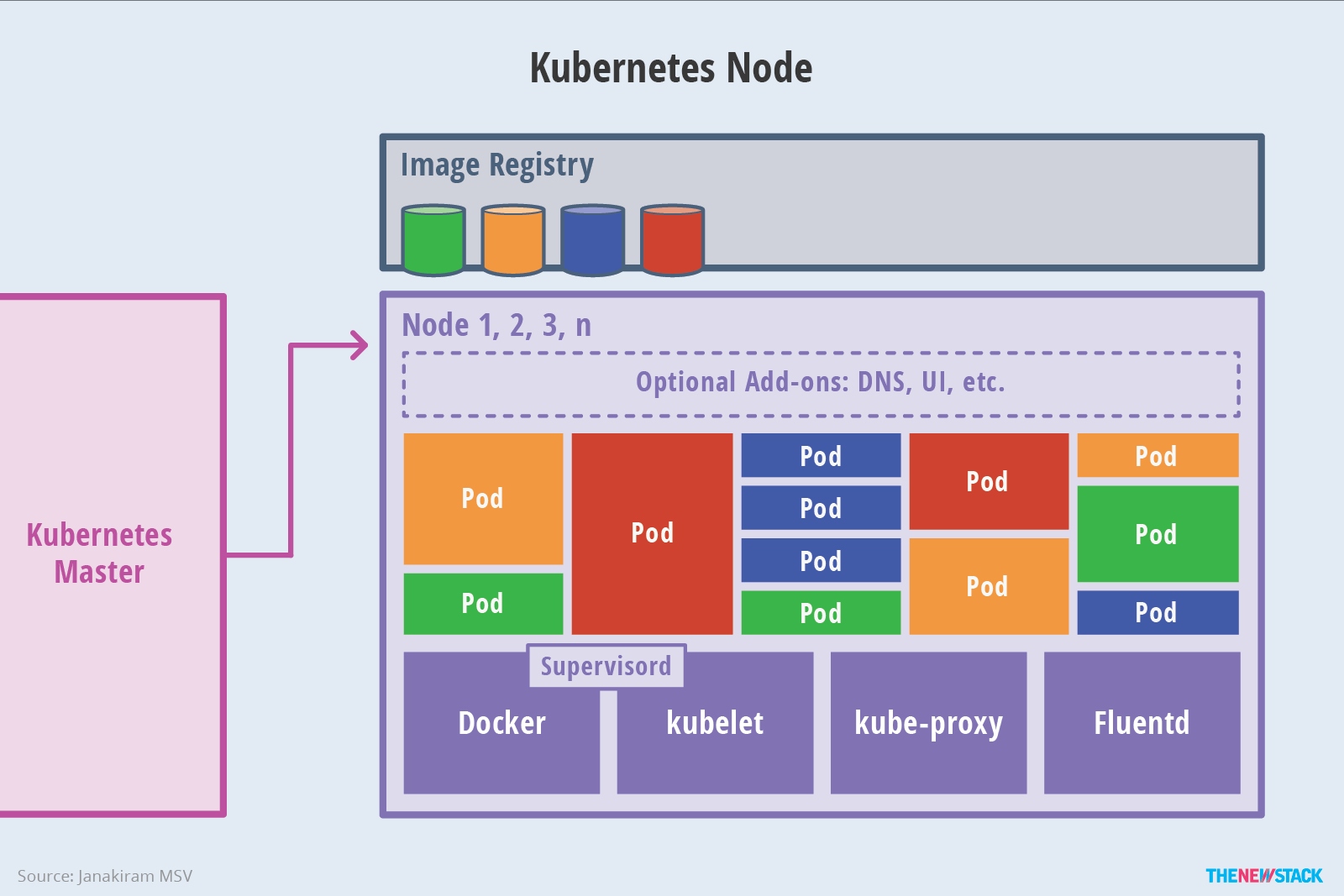
Kubernetes概述
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...

Jmeter教程
目录 安装与配置 一:下载jdk——配置jdk环境变量 二:下载JMeter——配置环境变量 安装与配置 一:下载jdk——配置jdk环境变量 1.新建环境变量变量名:JAVA_HOME变量值:(即JDK的安装路径) 2.编辑Path%J…...

用Rust实现23种设计模式之建造者模式
当使用 Rust 实现建造者模式时,我们可以通过结构体和方法链来实现。建造者模式是一种创建型设计模式,它允许你按照特定的顺序构建复杂对象,同时使你能够灵活地构建不同的变体。下面是一个使用 Rust 实现建造者模式的示例, 在示例中…...

聚观早报 | 腾讯字节等企业驰援防汛救灾;新能源车7月销量单出炉
【聚观365】8月4日消息 腾讯字节等企业驰援防汛救灾新能源车7月销量成绩单出炉Model Y等车型低温续航衰减严重华为Mate60系列猜想图曝光支付宝做短视频引来羊毛党 腾讯字节等企业驰援防汛救灾 近日,京津冀地区遭遇极端降雨天气,引发洪涝和地质灾害&…...
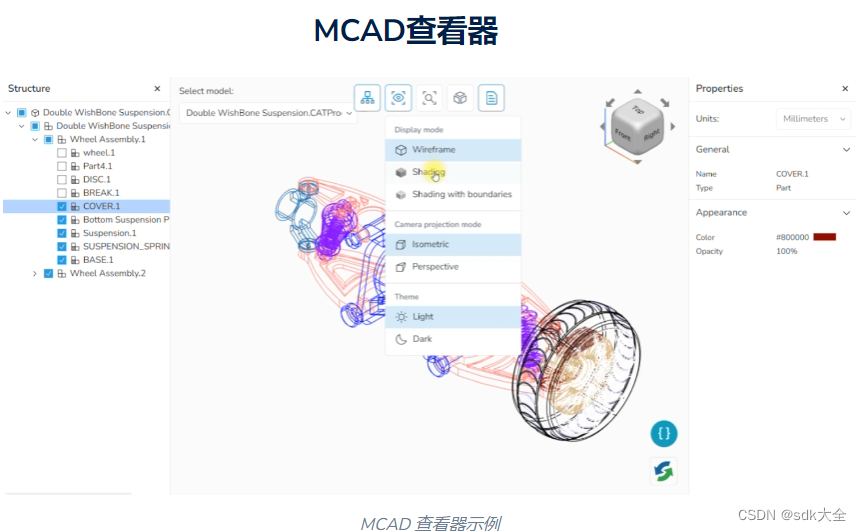
Crack:CAD Exchanger SDK 3.20 Web Toolkit 应用
在CAD Exchanger SDK 版本 3.20.0中,我们在 Web Toolkit 中包含了绘图、BIM 和 MCAD 查看器的示例,以展示如何使用每个工具可视化数据。这些查看器具有显示不同类型数据的特定功能,允许用户根据自己的需求单独使用它们。我们将继续增强每个查…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...