pktgen-dpdk arm编译问题 “Platform must be built with RTE_FORCE_INTRINSICS“
编译报错
/usr/include/rte_atomic_32.h:9:4: error: #error Platform must be built with RTE_FORCE_INTRINSICS
解决办法:
我是在 arm架构服务器上编译出现这个,要定义 RTE_FORCE_INTRINSICS
在meson.build中 增加gcc编译参数
add_project_arguments('-DRTE_FORCE_INTRINSICS', language: 'c')
相关文章:

pktgen-dpdk arm编译问题 “Platform must be built with RTE_FORCE_INTRINSICS“
编译报错 /usr/include/rte_atomic_32.h:9:4: error: #error Platform must be built with RTE_FORCE_INTRINSICS解决办法: 我是在 arm架构服务器上编译出现这个,要定义 RTE_FORCE_INTRINSICS 在meson.build中 增加gcc编译参数 add_project_arguments(…...

用html+javascript打造公文一键排版系统12:删除附件说明中“附件:”里的空格
如果我们在输入附件说明时在“附件:”之间加入空格,那么排版时就要删除这些空格。 因为string对象replace()支持正则表达式,于是考虑用replace()来完成。 写了一段只有一个多余空格的代码来测试: <!DOCTYPE HTML> <HT…...

容器技术:Docker搭建(通俗易懂)
目录 Docker搭建环境准备Docker安装1、查看服务器是否安装Docker2、卸载Docker3、安装Dokcer依赖环境4、配置Docker国内阿里云镜像5、安装Docker6、查看Docker信息7、配置阿里云镜像加速8、镜像安装10、运行实例11、查看实例状态12、测试 Docker命令集合 Docker搭建 环境准备 …...
)
Day 16 C++ 友元(friend)
目录 什么是友元(friend) 友元的三种实现 全局函数做友元 类做友元 成员函数做友元 什么是友元(friend) 友元是一种访问控制的机制,它允许一个类或函数访问另一个类的私有成员。通过友元关系,可以在需要…...

步进电机1
引脚说明: VCC:电源输入口 DC:9-42VDC:电源的取值范围 AB组:用于连接电机的四条线 STEP&PUL:脉冲信号接口,用于控制速度。无细分的情况下一个脉冲步进电机走一步。 DIR:方向信号接口&#x…...

PHP-简单项目引起的大麻烦--【白嫖项目】
强撸项目系列总目录在000集 PHP要怎么学–【思维导图知识范围】 文章目录 本系列校训本项目使用技术 首页小插曲小插曲完了么?必要的项目知识PHPThinkPHPThinkPHP的MVCThinkTemplateThinkPHP 6和ThinkPHP 5 phpStudy 设置导数据库展示页面数据库表结构项目目录如图…...
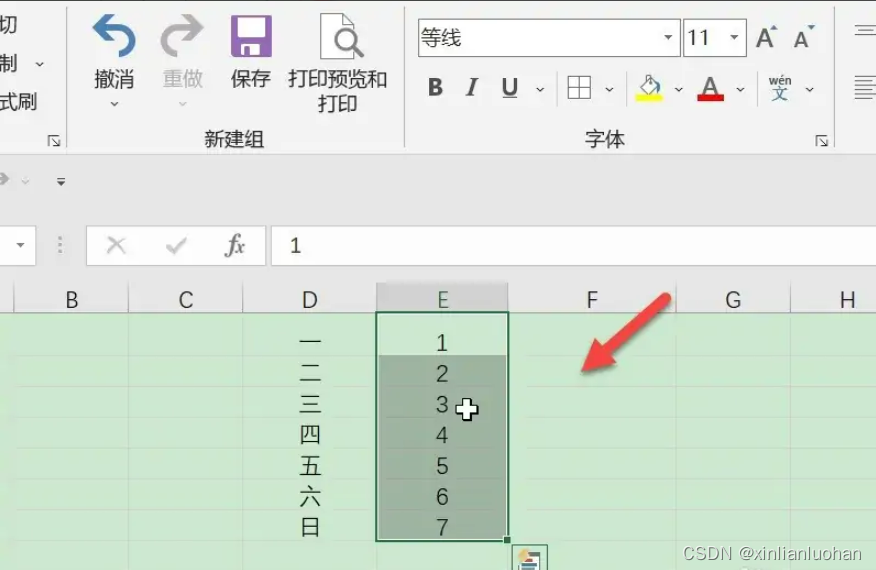
Excel如何把两列互换
第一步:选择一列 打开excel,选中一列后将鼠标放在列后,让箭头变成十字方向。 第二步:选择Shift键 按住键盘上的Shift键,将列往后移动变成图示样。 第三步:选择互换 完成上述操作后,松开鼠标两…...
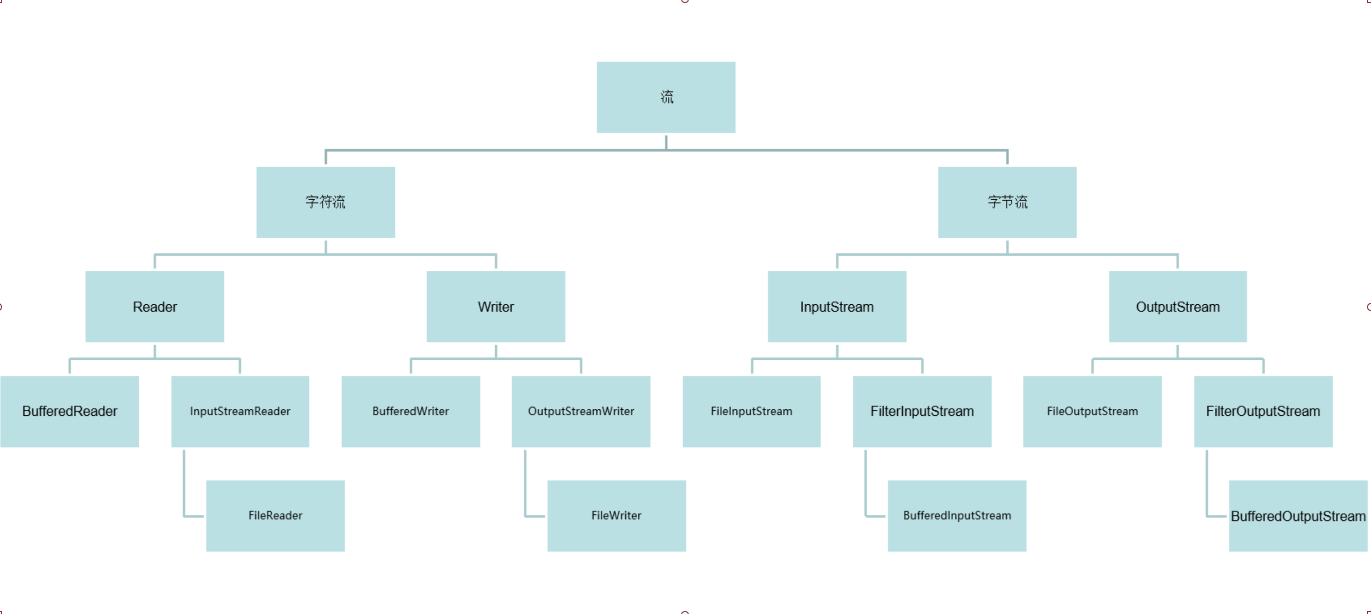
Java基础面试题2
Java基础面试题 一、IO和多线程专题 1.介绍下进程和线程的关系 进程:一个独立的正在执行的程序 线程:一个进程的最基本的执行单位,执行路径 多进程:在操作系统中,同时运行多个程序 多进程的好处:可以充…...
)
Typescript 第八章 异步编程,并行和并发(JavaScript事件循环,异步流,多线程类型安全)
Typescript第八章 异步编程,并发和并行 异步API,比如说回调,promise和流。 JavaScript引擎在一个线路中多路复用任务,而其他任务则处于空闲状态。这种事件循环是JavaScript引擎的标准线程模型。 多路复用是指在一个线程中同时处…...
)
c++ 打印当前时间(精确到毫秒)
打印时间精确到毫秒好实现,但是那种对用户可读性不好,更适合开头记一次结尾记一次,打印中间减出来的程序运行时间。 但是因为一些情况,我开多线程开的不方便打印结束时间,同事跟我说那你把开始时间打印一下࿰…...
mapstruct 错误 java.lang.NoSuchMethodError: Ljava/lang/Double 错误
问题描述 在使用 mapstruct 的过程中遇到错误 java.lang.NoSuchMethodError: Ljava/lang/Double 错误 问题解决 maven clean, 然后 maven install Build -> Rebuild Project 执行 maven install 时, 如果报错 找不到 xxx 类, 但 ctrl鼠标左键 发现可以点进去这个类, 那…...
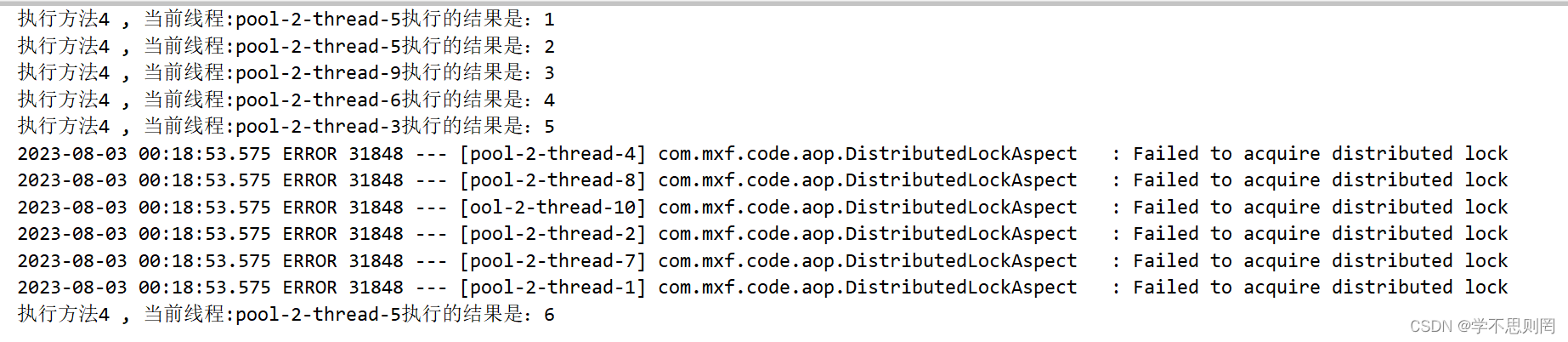
SpringBoot+AOP+Redission实战分布式锁
文章目录 前言一、Redission是什么?二、使用场景三、代码实战1.项目结构2.类图3.maven依赖4.yml5.config6.annotation7.aop8.model9.service 四、单元测试总结 前言 在集群环境下非单体应用存在的问题:JVM锁只能控制本地资源的访问,无法控制…...

Linux系统---进程概念
文章目录 冯诺依曼体系结构操作系统(OS)进程的理解 进程状态 进程优先级 环境变量 进程地址空间 Linux2.6内核进程调度队列 一、冯诺依曼体系结构 我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系。 如图…...

ELK常用语法和线上问题排查
ELK常用语法及线上问题排查 速查问题 1.全文搜索 在搜索栏输入目标值,查询所有字段中包含该值的文档 案例:用户反馈了一串id或者其他同事给了一个jobid,还没有头绪怎么查的时候,直接全局搜索 jobid 2.字段 限定字段全文搜索…...

session-cookies 三个缓存 localStorage、sessionStorage、Cookies。
session-cookies session-cookies This plugin is used to summarize the browser’s three caches localStorage, sessionStorage, Cookies.The plugin is designed to be quick and easy to use. Below is a summary of some apis. session-cookies 这个插件是用来汇总浏览…...

LA@行列式性质
文章目录 行列式性质🎈转置不变性质交换性质多重交换移动(抽出插入)👺 因子提取性质拆和性质倍加性质 手算行列式的主要方法原理:任何行列式都可以化为三角行列式 行列式性质🎈 设行列式 ∣ A ∣ d e t ( a i j ) |A|\mathrm{det}(a_{ij}) …...
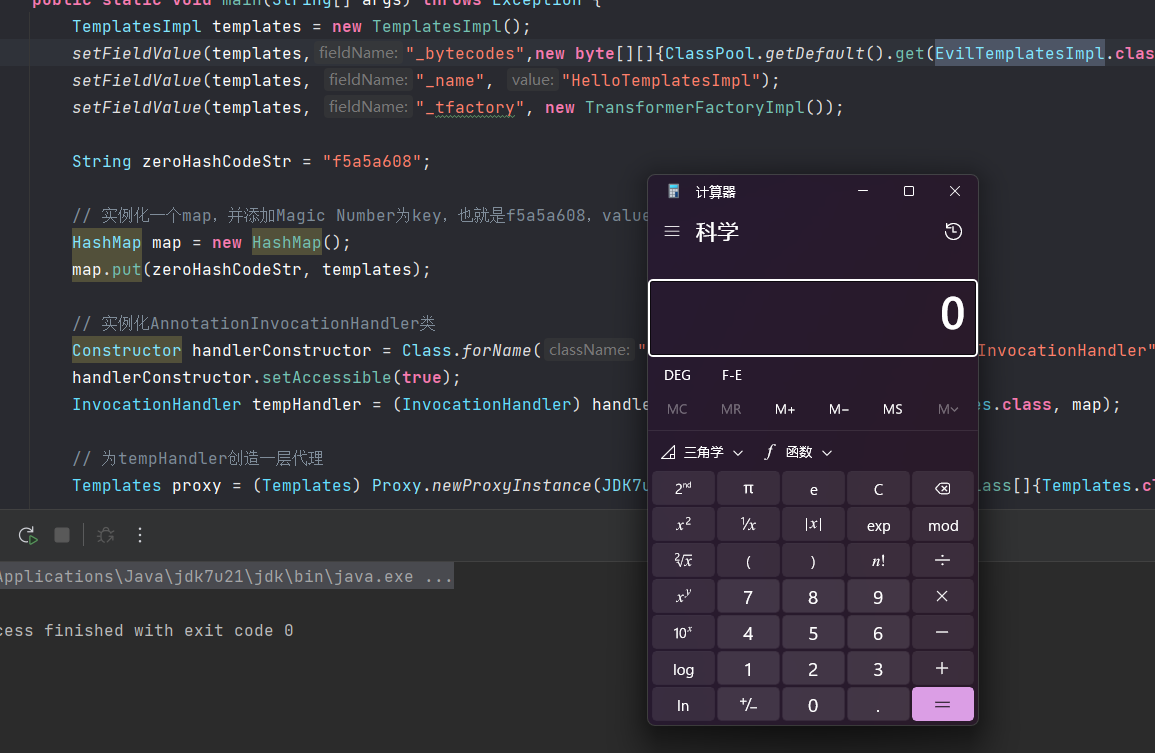
【java安全】原生反序列化利用链JDK7u21
文章目录 【java安全】原生反序列化利用链JDK7u21前言原理equalsImpl()如何调用equalsImpl()?HashSet通过反序列化间接执行equals()方法如何使hash相等? 思路整理POCGadget为什么在HashSet#add()前要将HashMap的value设为其他值? 【java安全】…...

[SQL智慧航行者] - SQL刷题规划
前言: 不知不觉, 慢慢的把一些基础知识整理到了现在. SQL挖掘机系列可能就要到此结束了. 目前是规划把这部分SQL练习部分放到SQL刷题的专栏, 就不放到SQL专栏了. 因为后续如果接触更多的知识点和题目也好分类. 请大家如果关注的话, 想看SQL知识点 --> SQL专栏; 想看SQL刷…...

概率论与数理统计:第一章:随机事件及其概率
文章目录 概率论Ch1. 随机事件及其概率1.基本概念(1)随机试验、随机事件、样本空间(2)事件的关系和运算①定义:互斥(互不相容)、对立②运算法则:德摩根率 (3)概率的定义(4)概率的性质(5)概率计算排列组合 2.等可能概型1.古典概型 (离散)2.几何概型 (连续…...

elementUi重置Select选择器样式、option、deep、vue3、plus
文章目录 前言select选框样式(element-plus)option选项面板样式(element-plus) 前言 样式标签属性为<style scoped lang"scss"></style> select选框样式(element-plus) // 设置选择框的背景样式 ::v-deep .el-input__wrapper {background: transparent;b…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
