数据结构—哈夫曼树及其应用
5.6哈夫曼树及其应用
5.6.1哈夫曼树的基本概念
路径:从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。
结点的路径长度:两结点间路径上的分支数。
树的路径长度:从树根到每一个结点的路径长度之和。记作 TL
结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树
权(weight):将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
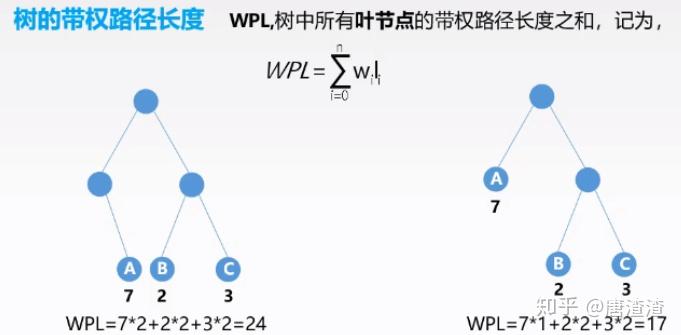
哈夫曼树:最优树 带权路径长度(WPL)最短的树
注意:“带权路径长度最短”是在“度相同”的树中比较而得的结果,因此有最优二叉树、最优三叉树之称等等。
哈夫曼树:最优二叉树 带权路径长度(WPL)最短的二叉树
因为构造这种树的算法是由哈夫曼教授于1952年提出的,所以被称为哈夫曼树,相应的算法称为哈夫曼算法。
哈夫曼树的特点:
满二叉树不一定是哈夫曼树
哈夫曼树中权越大的叶子离根越近
具有相同带权结点的哈夫曼树不唯一
5.6.2哈夫曼树的构造算法
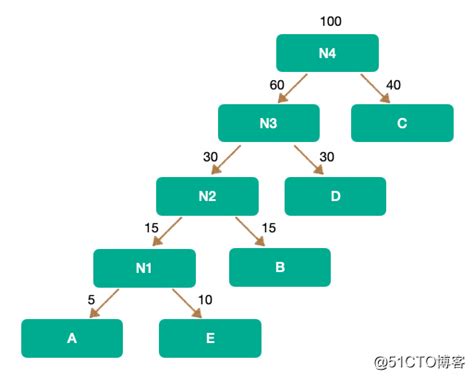
哈夫曼树中权越大的叶子离根越近
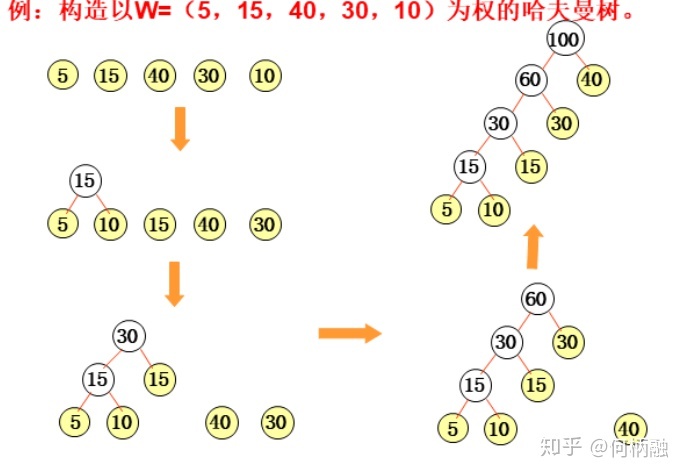
贪心算法:构造哈夫曼树时首先选择权值小的。
哈夫曼算法(构造哈夫曼树的方法)
- 根据 n 个给定的权值{W1,W2,…,Wn}构成 n 棵二叉树的森林F={T1,T2,…,Tn},其中Ti只有一个带权为Wi的根结点。
- 构造森林全是根
- 在F中选取两棵根结点的权值最小的树作为左右子树,构造一棵新的二叉树,且设置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
- 选用两小造新树
- 在F中删除这两棵树,同时将新得到的二叉树加入森林中。
- 删除两小添新人
- 重复(2)和(3),直到森林中只有一棵树为止,这棵树即为哈夫曼树。
- 重复2、3剩单根
哈夫曼树的结点的度数为0或2,没有度为1的结点。
包含 n 个叶子结点的哈夫曼树中共有 2n-1 个结点。
包含 n 棵树的森林要经过 n-1 次合并才能形成哈夫曼树,共产生 n-1 个新结点。

总结:
- 在哈夫曼算法中,初始时有 n 棵二叉树,要经过 n-1 次合并最终形成哈夫曼树。
- 经过 n-1 次合并产生 n-1 个新结点,且这 n-1 个新结点都是具有两个孩子的分支结点。
- 哈夫曼树中共有 n+n-1=2n-1 个结点,且其所有的分支结点的度均不为1。
5.6.3哈夫曼树构造算法的实现
采用顺序存储结构——一维结构数组
结点类型定义:
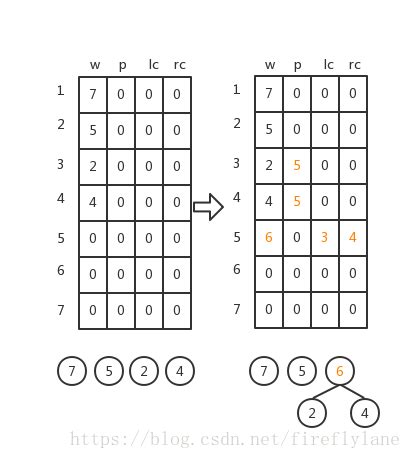
typedef struct{int weight;int parent,lch,rch;
}HTNode,*HuffmanTree;
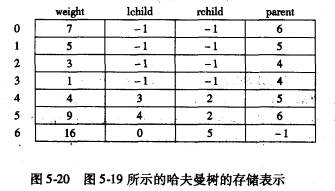
-
初始化HT[1…2n-1]:lch = rch = parent = 0;
-
输入初始 n 个叶子结点:置HT[1…n]的weight值;
-
进行一下n-1次合并,依次产生n-1个结点HT[i],i=n+1…2n-1:
a)在HT[1…i-1]中选两个未被选中(从parent==0的结点中选)的weight最小的两个结点HT[s1]和HT[s2],s1,s2为两个最小结点下标;
b)修改HT[s1]和HT[s2]的parent值:HT[s1].parent=i;HT[s2].parent=i;
c)修改新产生的HT[i]:
- HT[i].weight=HT[s1].weight + HT[s2].weight;
- HT[i].lch=s1;HT[i].rch=s2
void CreatHuffmanTree (HuffmanTree HT,int n){if(n<=1)return;m=2*n-1;//数组共有2n-1个元素HT=new HTNode[m+1];//0号单元未用,HT[m]表示根结点for(i=0;i<=m;++i){//将2n-1个元素的lch,rch,parent置为0HT[i].lch=0;HT[i].rch=0;HT[i].parent=0;}for(i=1;i<=n;++i)//输入前n个元素的weightcin>>HT[i].weight;for(i=n+1;i<=m;i++){Select(HT,i-1;s1,s2);//在HT[k]中选择两个其双亲域为0,且权值最小的结点,并返回他们在HT中的序号s1和s2HT[s1].parent=i;//表示从F中删除s1,s2HT[s2].parent=i;HT[i].lch=s1;HT[i].rch=s2;HT[i].weigth=HT[s1].weigth+HT[s2].weigth;}
}
5.6.4哈夫曼编码
在远程通讯中,要将待传字符转换成由二进制表示的字符串:
若将编码设计为长度不等的二进制编码,即让待传字符串中出现次数较多的字符采用尽可能短的编码,则转换的二进制字符串便可能减少。
关键:要设计长度不等的编码,则必须使任一字符的编码都不是另一个字符的编码的前缀。——这种编码称做前缀编码。
问题:什么样的前缀码能使得电文总长最短?——哈夫曼编码
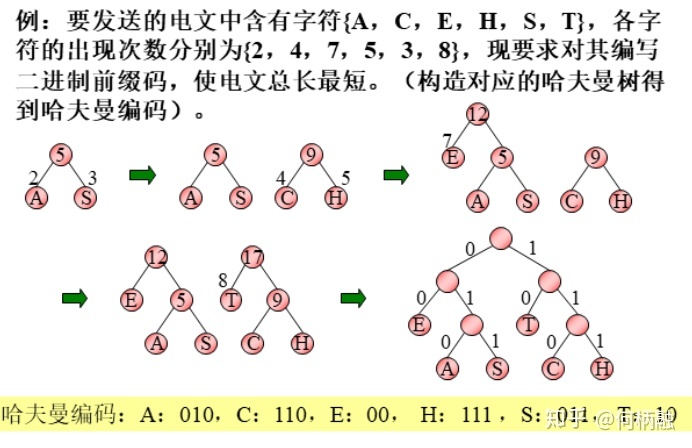
- 统计字符集中每个字符在电文中出现的平均概率(概率越大,要求编码越短)。
- 利用哈夫曼树的特点:权越大的叶子离根越近;将每个字符的概率值作为权值,构造哈夫曼树。则概率越大的结点,路径越短。
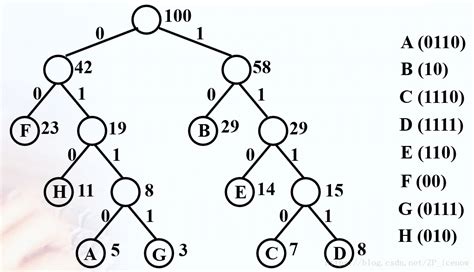
- 在哈夫曼树的每个分支上标上0或1:
- 结点的左分支标0,右分支标1
- 把从根到每个叶子的路径上的标号连接起来,作为该叶子代表的字符的编码。
两个问题:
为什么哈夫曼编码能够保证是前缀编码?
因为没有一片树叶是另一片树叶的祖先,所以每个叶节点的编码就不可能是其他叶节点编码的前缀。
为什么哈夫曼编码能够保证字符编码总长最短?
因为哈夫曼树的带权路径长度最短,故字符编码的总长最短。
哈夫曼编码的性质
- 性质1:哈夫曼编码是前缀码
- 性质2:哈夫曼编码是最优前缀码
5.6.5哈夫曼编码的算法实现

void CreatHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n){//从叶子到根逆向求每个字符的哈夫曼编码,存储在编码表HC中HC=new char*[n+1];//分配n个字符编码的头指针矢量cd=new char [n];//分配临时存放编码的动态数组空间cd[n-1]='\0';//编码结束符for(i=1;i<=n;i++){//逐个字符求哈夫曼编码start=n-1;c=i;f=HT[i].parent;while(f!=0){//从叶子结点开始向上回溯,直到根结点--start;//回溯一次start向前指一个位置if(HT[f].lchild==c)cd[start]='0';//结点c是f的左孩子,则生成代码0else cd[start]='1';//结点c是f的右孩子,则生成代码1c=f;//继续向上回溯f=HT[f].parent;}HC[i]=new char[n-start];//为第i个字符串编码分配空间strcpy(HC[i],&cd[start]);//将求得的编码从临时空间cd复制到HC的当前行中}delete cd;
}
5.6.6文件的编码和解码
1、编码
① 输入各字符及其权值
② 构造哈夫曼树——HT[i]
③ 进行哈夫曼编码——HC[i]
④ 查HC[i],得到各字符的哈夫曼编码
2、解码
① 构造哈夫曼树
② 依次读入二进制码
③ 读入0,则走向左孩子;读入1,则走向右孩子
④ 一旦到达某叶子时,即可译出字符
⑤ 然后再从根出发继续译码,直到结束。
相关文章:

数据结构—哈夫曼树及其应用
5.6哈夫曼树及其应用 5.6.1哈夫曼树的基本概念 路径:从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。 结点的路径长度:两结点间路径上的分支数。 树的路径长度:从树根到每一个结点的路径长度之和。记作 TL 结点数目相同的…...

NeRF-SLAM: Real-Time Dense Monocular SLAM with Neural Radiance Fields 论文阅读
论文信息 题目:NeRF-SLAM: Real-Time Dense Monocular SLAM with Neural Radiance Fields 作者:Antoni Rosinol, John J. Leonard, Luca Carlone 代码:https://github.com/ToniRV/NeRF-SLAM 来源:arxiv 时间ÿ…...
)
机器学习之弹性网络(Elastic Net)
弹性网络 代码原文 下面代码参考scikit-learn中文社区,链接在上面。 但是由于scikit-learn中文社区上的代码有些地方跑不通,故对此代码做了修改,输出结果与社区中显示的结果相同。 对弹性网络进行简单的介绍: ElasticNet是一个训…...

嵌入式入门教学——C51
一、前期准备 1、硬件设备 2、软件设备 二、预备知识 1、什么是单片机? 在一片集成电路芯片上集成微处理器、存储器、IO接口电路,从而构成了单芯片微型计算机,及单片机。STC89C52单片机: STC:公司89:所属…...

2023-08-03力扣每日一题
链接: 722. 删除注释 题意: 如题,特殊规则见链接 解: 字符串处理,嗯写就完事了,主要是判断指针位置和特殊规则 实际代码: #include<bits/stdc.h> using namespace std; vector<string> …...

【蓝桥杯备考资料】如何进入国赛?
目录 写在前面注意事项数组、字符串处理BigInteger日期问题DFS 2013年真题Java B组世纪末的星期马虎的算式振兴中华黄金连分数有理数类(填空题)三部排序(填空题)错误票据幸运数字带分数连号区间数 2014年真题蓝桥杯Java B组03猜字…...
QtWebApp开发https服务器,完成客户端与服务器基于ssl的双向认证
引言:所谓http协议,本质上也是基于TCP/IP上服务器与客户端请求和应答的标准,web开发中常用的http server有apache和nginx。Qt程序作为http client可以使用QNetworkAccessManager很方便的进行http相关的操作。Qt本身并没有http server相关的库…...

动态IP代理的优势展现与应用场景
在当今数字化时代,网络安全和隐私保护变得愈发重要。作为一家动态IP代理产品供应商,我们深知在保护个人隐私和提高网络安全性方面的重要性。本文将会分享动态IP代理的优势及其在不同应用场景下的实际应用案例,帮助更好地了解和应用动态IP代理…...
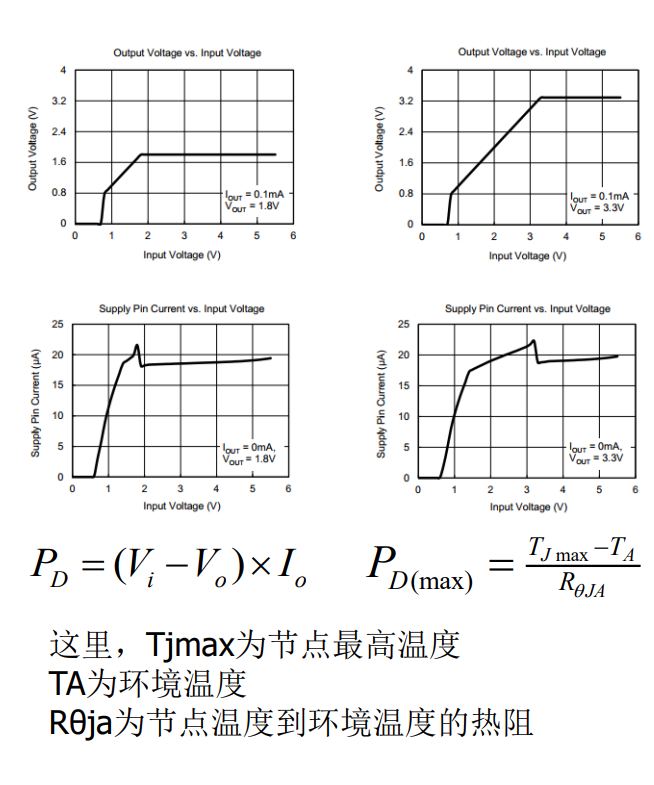
ad+硬件每日学习十个知识点(22)23.8.2(LDO datasheet手册解读)
文章目录 1.LDO的概述、features2.LDO的绝对参数(功率升温和结温)3.LDO的引脚功能4.LDO的电气特性5.LDO的典型电路(电容不能真用1uF,虽然按比例取输出值,但是R2的取值要考虑释放电流)6.LDO的开关速度和线性…...

这可是全网最全的网络工程师零基础实战视频整理,最新版分享
互联网中每一项傍身的技能都是需要从如何入门开始的,网络技术也是如此! 网络技术区别其他互联网技能的一点是学习需要从设备开始,只有认识了解了路由器、交换机、防火墙这些网络设备,才开始从网络通信原理开始,这使得网…...
笔记本WIFI连接无网络【实测有效解决方案,不用重启电脑】
笔记本Wifi连接无网络实测有效解决方案 问题描述: 笔记本买来一段时间后,WIFI网络连接开机一段时间还正常连接,但是过一段时间显示网络连接不上解决方案: 1.编写网络重启bat脚本,将以下内容写到文本文件,把…...

js 正则表达式配合replace进行过滤html字符串遇到的性能问题
问题场景复现: 博主要实现一个邮箱列表,其中列表中的每一封邮件都有一个摘要,但是摘要是要自己从后端提供的content内容区自己过滤掉所有,只留下纯文本内容的前面几行作为摘要。 性能问题 当我测试到一个邮箱,其中的…...

2022牛客寒假算法基础集训营1
B题 炸鸡块君与FIFA22 题目大意: 给出胜负序列,每次询问区间 (l,r,s) ,回答在经历 (l-r) 之后积分是多少,初始积分为 (s) 胜 (1) 积分,平 (0) 积分,败的时候如果此时积分为 (3) 的倍数则 (-0) ,…...

API对接:构建连接不同系统的技术桥梁
API(Application Programming Interface)是一种用于不同软件系统之间进行通信和数据交换的技术。本文将介绍API对接的基本概念和原理,并通过代码示例演示如何使用API对接不同系统,解决数据传输与通信的难题。 在当今数字化时代&a…...
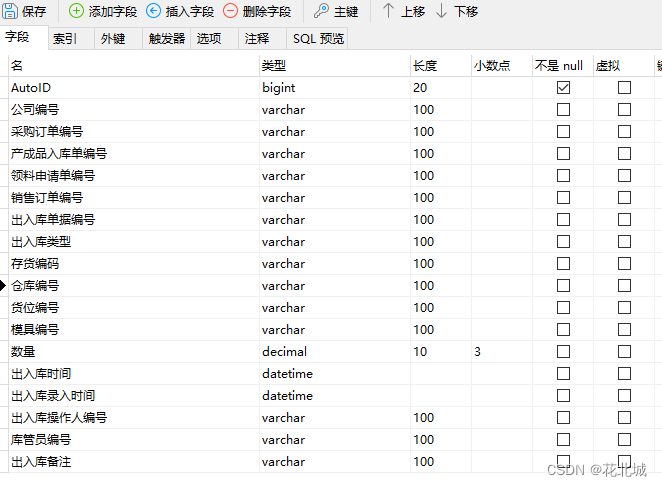
【MySQL】仓储--维护出入库流水、库存,去重数量逻辑修正
系列文章 C#底层库–MySQLBuilder脚本构建类(select、insert、update、in、带条件的SQL自动生成) 本文链接:https://blog.csdn.net/youcheng_ge/article/details/129179216 C#底层库–MySQL数据库操作辅助类(推荐阅读࿰…...

用Log4j 2记录日志
说明 maven工程中增加对Log4j 2的依赖 下面代码示例的maven工程中的pom.xml文件中需要增加对Log4j 2的依赖: <dependency><groupId>org.apache.logging.log4j</groupId><artifactId>log4j-core</artifactId><version>2.20.0&…...

【Java面试】Paxos和Raft协议的区别?
面试官:你简历上说了解Paxos和Raft协议,说一下你对这两个协议的了解? 我:Paxos算法和Raft算法都是用于实现分布式系统中的一致性的算法,确保不同节点之间的数据一致。 我:Paxos算法它的目标是使多个节点能…...

手机浏览器H5打开微信小程序支付,自定义传参
微信官方提供的开放文档如下: 静态网站 H5 跳小程序 | 微信开放文档 想必大家都能看懂官网提供的文档,但实战时却遇到很多问题,博主总结一下遇到的坑,如果您也有遇到,希望可以帮到您。 1.小程序已经发布上线了&…...
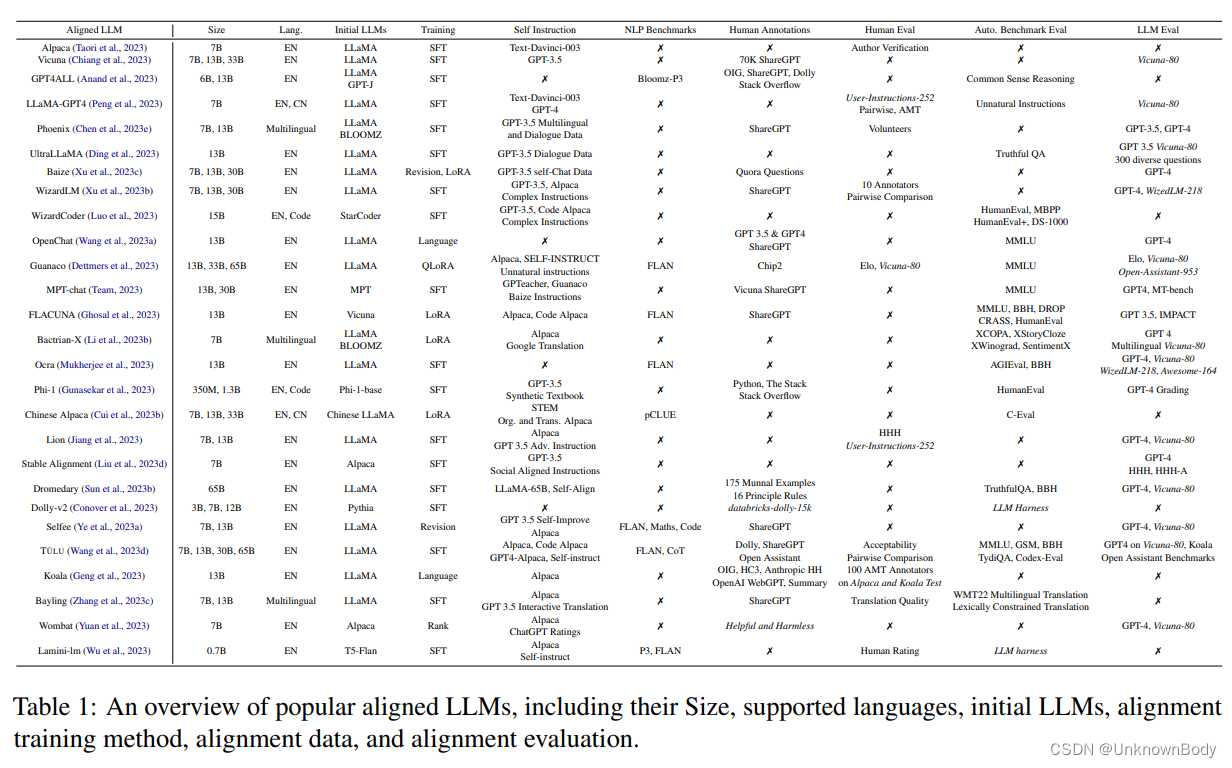
Aligning Large Language Models with Human: A Survey
本文也是LLM相关的综述文章,针对《Aligning Large Language Models with Human: A Survey》的翻译。 对齐人类与大语言模型:综述 摘要1 引言2 对齐数据收集2.1 来自人类的指令2.1.1 NLP基准2.1.2 人工构造指令 2.2 来自强大LLM的指令2.2.1 自指令2.2.2 …...
windows图标白了,刷新图标
1.进入C盘,user(用户文件夹),进入当前用户文件夹,再进入隐藏文件夹(AppDada),最后进入Local 2.删除Local文件夹里的IconCache.db文件 3.重启资源管理器 -------------------------------------------- 或者创建bat文件…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
