【深度学习_TensorFlow】误差函数
写在前面
搭建完网络层后,在每层网络中都要进行前向计算,下一步就是选择合适的误差函数来计算误差。其中均方差函数和交叉熵函数在深度学习中比较常见,均方差函数主要用于回归问题,交叉熵函数主要用于分类问题。
写在中间
均方差函数
( 1 )简单介绍
均方差函数(简称 MSE)把输出向量和真实向量映射到笛卡尔坐标系的两个点上,通过计算这两个点之间的欧式距离(准确地说是欧式距离的平方)来衡量两个向量之间的差距:
M S E ( y , o ) ≜ 1 d o u t ∑ i = 1 d o u t ( y i − o i ) 2 \mathrm{MSE}(\boldsymbol{y},\boldsymbol{o})\triangleq\frac{1}{d_{\mathrm{out}}}\sum_{i=1}^{d_{\mathrm{out}}}(y_i-o_i)^2 MSE(y,o)≜dout1∑i=1dout(yi−oi)2
MSE 误差函数的值总是大于等于 0,值越小,越接近真实值。
当 MSE 函数达到最小值 0 时,输出值等于真实标签,此时神经网络的参数达到最优状态。
( 2 )函数实现
# 均方差函数的实现有多种
import tensorflow as tf# 方法一:
tf.reduce_mean(tf.square(y_true - y_pred))# 方法二:
tf.keras.losses.MSE(y_true, y_pred)交叉熵函数
介绍交叉熵函数之前,我们先了解 熵 和 KL散度 这两个概念
熵
熵用来衡量信息的不确定度,熵越大,代表不确定性越大。
公式如下:
H ( P ) ≜ − ∑ i P ( i ) log 2 P ( i ) H(P)\triangleq-\sum_iP(i)\log_2P(i) H(P)≜−∑iP(i)log2P(i)
熵的计算
熵怎样计算?对于分类问题:
- 如果某个样本的标签的 One-hot 编码为[0, 0, 0, 1],即这张图片的分类是唯一确定的,不确定性为 0。它属于第 4 类的概率𝑃(𝑦为 4|𝒙) = 1,此标签的熵可以简单的计算为:
− 0 ⋅ log 2 0 − 0 ⋅ log 2 0 − 0 ⋅ log 2 0 − 1 ⋅ log 2 1 = 0 -0\cdot\log_20-0\cdot\log_20-0\cdot\log_20-1\cdot\log_21=0 −0⋅log20−0⋅log20−0⋅log20−1⋅log21=0
- 如果某个样本的标签的 One-hot 编码为[0.1, 0.1, 0.1, 0.7],即这张图片的分类属于第四类的概率较大,此标签的熵就可以计算为:
− 0.1 ⋅ log 2 0.1 − 0.1 ⋅ log 2 0.1 − 0.1 ⋅ log 2 0.1 − 0.7 ⋅ log 2 0.7 ≈ 1.356 -0.1\cdot\log_20.1-0.1\cdot\log_20.1-0.1\cdot\log_20.1-0.7\cdot\log_20.7\approx1.356 −0.1⋅log20.1−0.1⋅log20.1−0.1⋅log20.1−0.7⋅log20.7≈1.356
很明显,第二个结果的熵比第一个熵大,不确定度也大得多,因此最小化熵的过程也是最大化正确类别的预测概率的过程。从这个角度去理解交叉熵损失函数,非常地直观易懂。
KL散度
如果我们对于同一个随机变量 i 有两个单独的概率分布 p(i) 和 q(i),我们可以使用 KL 散度来衡量这两个分布的差异:
在深度学习中,我们通常把真实的标签分布(通常是 one-hot 编码)视为 p,把模型预测的概率分布视为 q。
KL散度的计算公式为
D K L ( p ∣ ∣ q ) = ∑ i p ( i ) l o g ( p ( i ) q ( i ) ) D_{KL}(p||q)=\sum_{i}p(i)\mathrm{log}\left(\frac{p(i)}{q(i)}\right) DKL(p∣∣q)=∑ip(i)log(q(i)p(i))
我们仍然使用上面的例子,标签的one-hot编码为[0, 0, 0, 1],预测值为[0.1, 0.1, 0.1, 0.7],KL散度计算结果为:
KL = 0 * log(0/0.1) + 0 * log(0/0.1) + 0 * log(0/0.1) + 1 * log(1/0.7)
= -log(0.7)
≈ 0.357
交叉熵
终于要介绍交叉熵了,你一定会猜到讲上面的知识会和交叉熵有关,对你猜的没错!
交叉熵损失函数的计算公式为:
H ( p ∣ ∣ q ) = H ( p ) + D K L ( p ∣ ∣ q ) H(p||q)=H(p)+D_{KL}(p||q) H(p∣∣q)=H(p)+DKL(p∣∣q)
其实就是熵和KL散度的加和,稍加变形就得到:
H ( p ∣ ∣ q ) ≜ − ∑ i p ( i ) log 2 q ( i ) H(p||q)\triangleq-\sum_ip(i)\log_2q(i) H(p∣∣q)≜−∑ip(i)log2q(i)
交叉熵函数的实现
import tensorflow as tf# 假设 y_true 是真实的标签,y_pred 是模型的预测值
y_true = [[0, 0, 0, 1], [0, 1, 0, 0]]
y_pred = [[0.1, 0.1, 0.1, 0.7], [0.1, 0.6, 0.1, 0.2]]loss = tf.keras.losses.categorical_crossentropy(y_true, y_pred)
写在最后
👍🏻点赞,你的认可是我创作的动力!
⭐收藏,你的青睐是我努力的方向!
✏️评论,你的意见是我进步的财富!
相关文章:

【深度学习_TensorFlow】误差函数
写在前面 搭建完网络层后,在每层网络中都要进行前向计算,下一步就是选择合适的误差函数来计算误差。其中均方差函数和交叉熵函数在深度学习中比较常见,均方差函数主要用于回归问题,交叉熵函数主要用于分类问题。 写在中间 均方差…...
mysql按照日期分组统计数据
目录 前言按天统计按周统计按月统计按年统计date_format参数 前言 mysql的date_format函数想必大家都使用过吧,一般用于日期时间转化 # 例如 select DATE_FORMAT(2023-01-01 08:30:50,%Y-%m-%d %H:%i:%s) # 可以得出 2023-01-01 08:30:50# 或者是 select DATE_FOR…...

19 | 分类模型评估指标
文章目录 Python分类模型评估指标准确率(Accuracy)精确率(Precision)召回率(Recall)F1值(F1 Score)混淆矩阵(Confusion Matrix)ROC曲线和AUC值1. 准备数据集2. 初始化并训练逻辑回归模型3. 获取预测概率并计算ROC曲线和AUC值4. 绘制ROC曲线5. 整合代码结论Python分类…...

【Pycharm2022.2.1】python编辑器最新版安装教程(包含2017-2022的所有版本win/mac/linux)
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 永久安装 Pycharm(2017-2022的win/mac/linux所有版本)/ IntelliJ IDEA也可以, 按照本文教程所写的,具体步骤跟着下面的图文教程一步一步来就行,一分钟即可搞定,过…...

深度学习-相关概念
Adam优化器 Adam,Adaptive Moment Estimation,自适应矩估计。是2014年提出的一种万金油式的优化器,使用起来非常方便,梯度下降速度快,但是容易在最优值附近震荡。竞赛中性能会略逊于SGD,毕竟最简单的才是最…...

眼科医生推荐的台灯 护眼台灯买什么好?
我家孩子需要一个护眼灯,就请教了我的一个医生朋友。大家都知道医生白天对着电脑长时间的工作,晚上还要看书,查文献,写论文,选一个对眼睛友好的高质量护眼台灯对他们是刚需,同时又是医生,所以他…...

如何使用 ChatGPT 为 Midjourney 或 DALL-E 等 AI 图片生成提示词
人工智能为创意产业开辟了一个充满可能性的全新世界。人工智能最令人兴奋的应用之一是生成独特且原创的艺术品。Midjourney 和 DALL-E 是人工智能生成艺术的两个突出例子,吸引了艺术家和艺术爱好者的注意。在本文中,我们将探索如何使用 ChatGPT 生成 AI …...
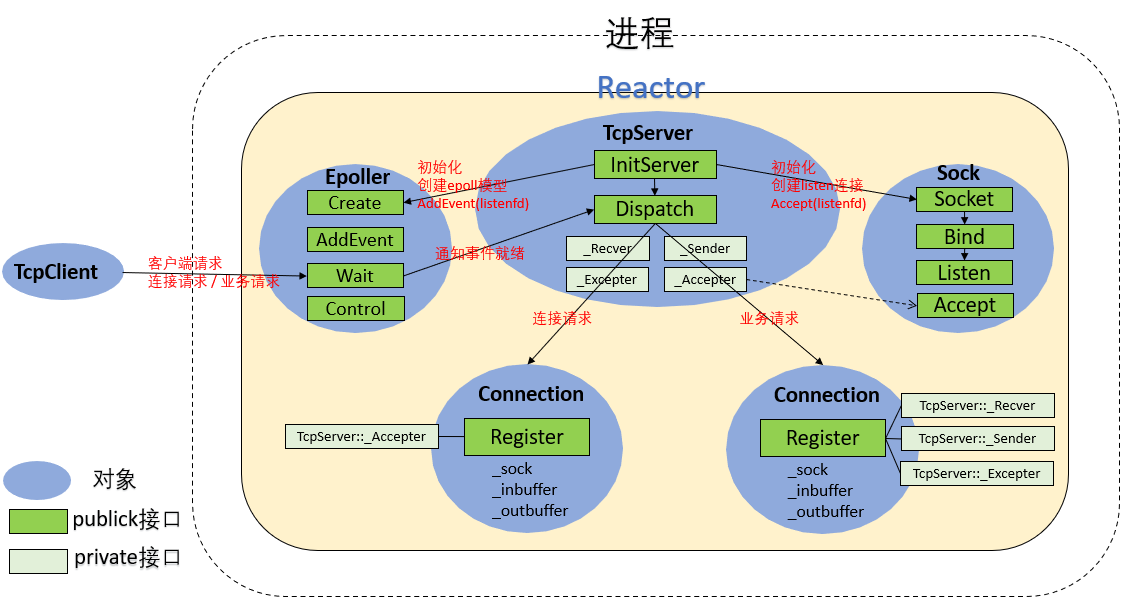
【Linux后端服务器开发】Reactor模式实现网络计算器
目录 一、Reactor模式概述 二、日志模块:Log.hpp 三、TCP连接模块:Sock.hpp 四、非阻塞通信模块:Util.hpp 五、多路复用I/O模块:Epoller.hpp 六、协议定制模块:Protocol.hpp 七、服务器模块:Server.…...

【WebRTC---源码篇】(二:一)PeerConnection详解
Track的添加 上图是整体流程图 RTCErrorOr<rtc::scoped_refptr<RtpSenderInterface>> PeerConnection::AddTrack(rtc::scoped_refptr<MediaStreamTrackInterface> track,const std::vector<std::string>& stream_ids) {RTC_DCHECK_RUN_ON(signal…...

使用tinyxml解析和修改XML文件
首先要清楚XML文件包含哪些元素: 他是由元素、文本或者两者混合物组成。元素可以拥有属性,元素是指从开始标签到结束标签的部分。 <?xml version"1.0" encoding"UTF-8" ?> <books><book id"1001">&…...
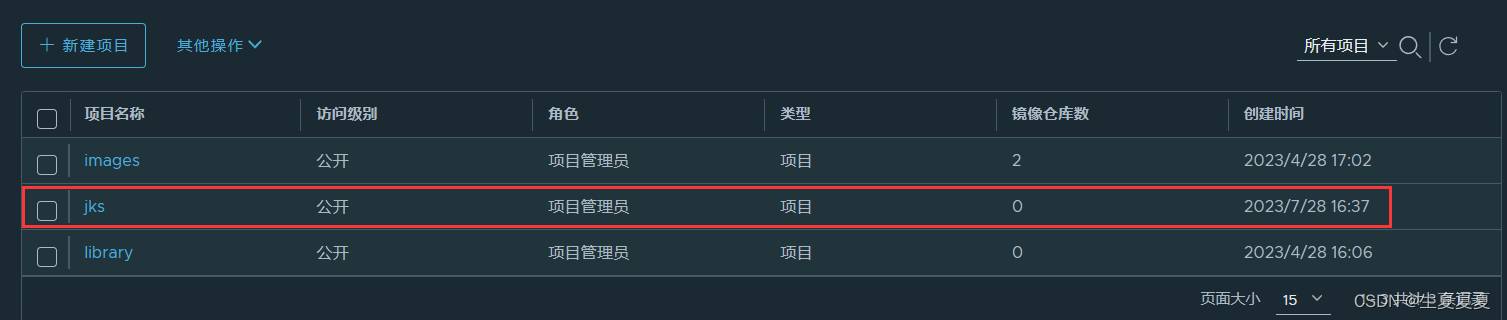
[Docker实现测试部署CI/CD----相关服务器的安装配置(1)]
目录 0、CI/CD系统最终架构图规划IP地址 1、git配置Git下载pycharm配置gitidea配置git 2、GitLab安装与配置主机要求拉取镜像定义 compose.yml启动gitlab浏览器访问并修改密码查看登录密码修改密码 3、SonarQube 安装与配置拉取镜像修改虚拟内存的大小启动SonarQube登录 SonarQ…...
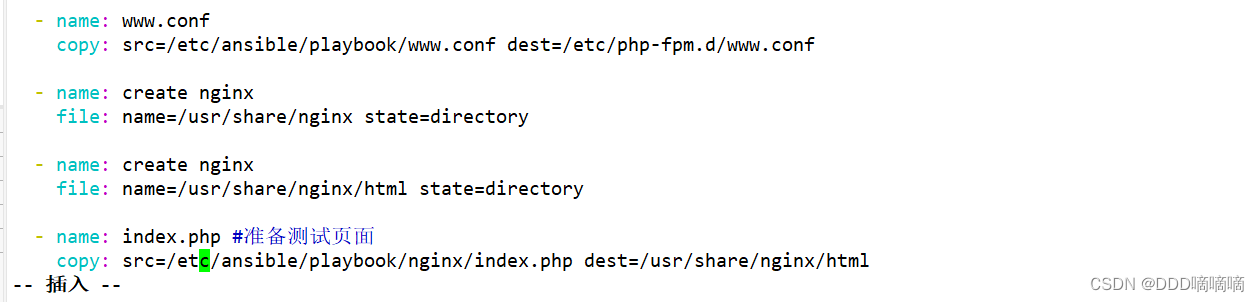
【自动化运维】编写LNMP分布式剧本
目录 一 playbook编写LNMP1.1环境设置1.2编写Nginx剧本1.3、编写Mysql剧本1.4准备PHP剧本 一 playbook编写LNMP 1.1环境设置 ip服务192.168.243.100ansible192.168.243.102nginx192.168.243.103PHP192.168.243.104mysql 1.2编写Nginx剧本 1.编写Nginx源 mkdir -p /etc/ans…...

用Rust实现23种设计模式之单例
话不多说,上代码! 1. 使用Arc Mutex 在这个例子中,我们使用了 Arc (原子引用计数)和 Mutex (互斥锁)来实现线程安全的单例。通过 get_instance 方法,我们可以获取到单例实例&…...
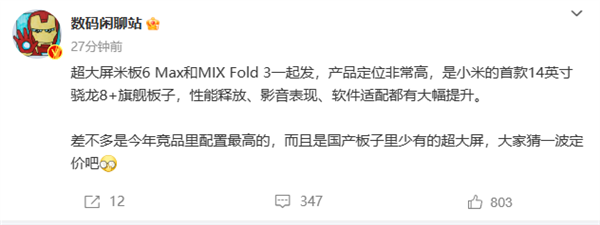
小米平板6将推14英寸版!与MIX Fold 3同步推出
今天,知名数码博主数码闲聊站爆料消息,称小米平板6将推出一款Max版本,预计与小米MIX Fold 3同步推出。 据介绍,小米平板6 Max将是小米首款14英寸大屏的旗舰平板,平板搭载骁龙8处理器,在性能释放、影音表现、…...

webpack 的一点知识
多个入口共享多个模块 在使用webpack搭建多页面应用时候需要多个入口,这个时候需要考虑到模块共享问题了 可以使用entry.dependOn 来处理 entry: {home: {import: "./pages/home/index.js",// 其中vendors里边使用到模块,不会打入home对应的…...
)
Python 双目摄像机控制(windows + linux)
一、Windows 下载 Download libusb-win32-devel-filter-1.2.6.0.exe (libusb-win32) 安装,在弹出框中选择摄像机usb设备 pip install pyusb pip install libusb 代码如下,注意如果报错要以管理员权限运行: import cv2 import usb.corecam…...
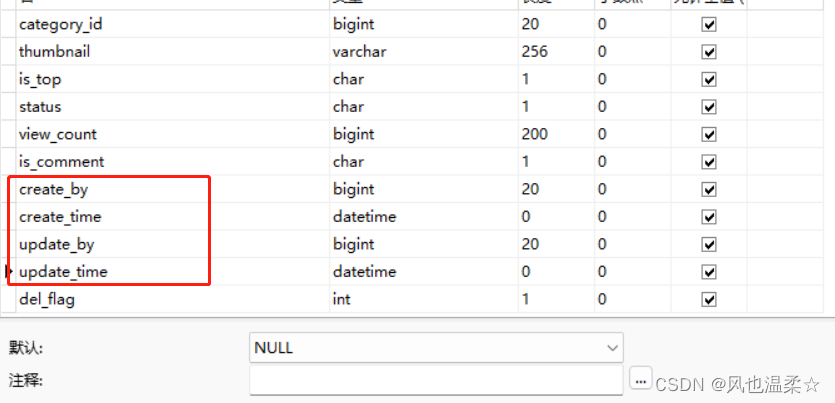
mybatisplus实现自动填充 时间
mybatisplus实现自动填充功能——自动填充时间 数据库表中的字段 创建时间 (createTime)更新时间 (updateTime) 每次 增删改查的时候,需要通过对Entity的字段(createTime,updateTime)进行set设置,但是,每…...

P5732 【深基5.习7】杨辉三角
题目描述 给出 n ( n ≤ 20 ) n(n\le20) n(n≤20),输出杨辉三角的前 n n n 行。 如果你不知道什么是杨辉三角,可以观察样例找找规律。 输入格式 输出格式 样例 #1 样例输入 #1 6样例输出 #1 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 11.题目…...
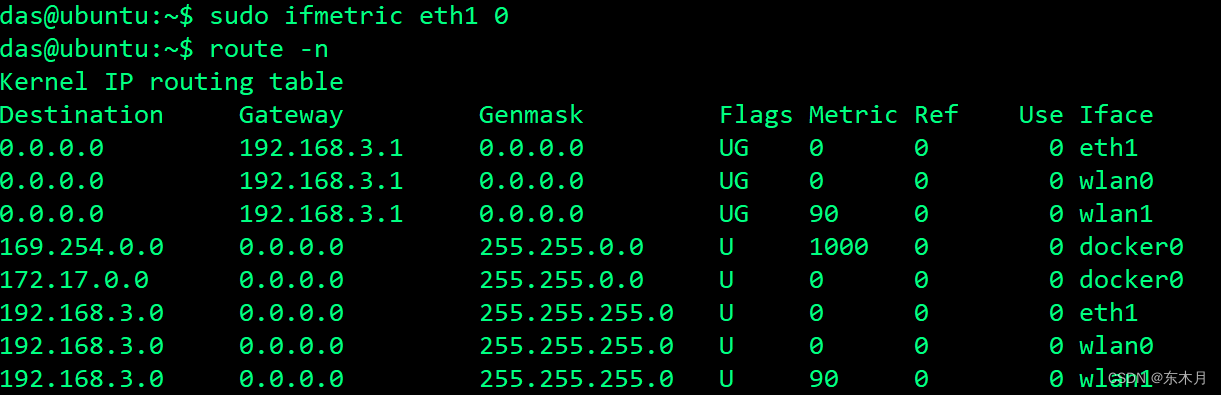
ubuntu调整路由顺序
Ubuntu系统跳转路由顺序 1、安装ifmetric sudo apt install ifmetric2、查看路由 route -n3、把Iface下面的eth1调到第一位 sudo ifmetric eth1 0命令中eth1是网卡的名称,更改网卡eth1的跃点数(metric值)为0(数值越小…...
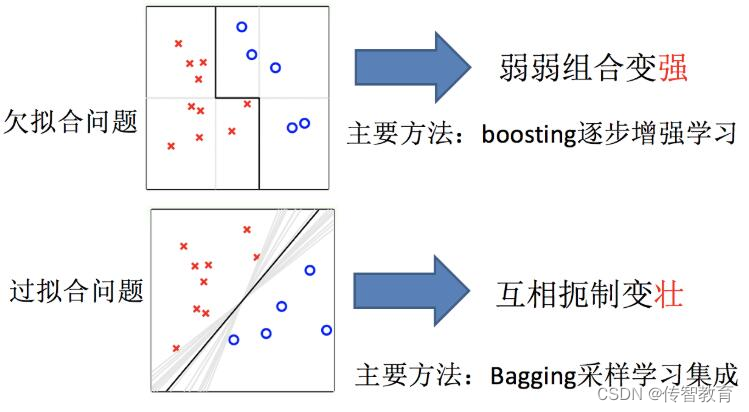
集成学习算法是什么?如何理解集成学习?
什么是集成学习? 集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测。 机器学习的两个核心任务 任务一࿱…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
