【力扣刷题 | 第二十四天】

目录
前言:
416. 分割等和子集 - 力扣(LeetCode)
总结
前言:
今晚我们爆刷动态规划类型的题目。
416. 分割等和子集 - 力扣(LeetCode)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。

这道题其实可以用我们之前讲过的回溯算法暴力搜索来做,其基本思想为:我们先对这个数组求和,之后再除以二,此时如果我们如果我们得到了一个整数,就说明这个数组是可以分为两个元素和一样的子集的,如果得不到就说明这个数组根本就没有办法被均分,自然也就无法得到两个元素和一样的子集。
那么也就是说把这个集合的总和的一半target求出来,然后在集合中搜索,如果可以在原集合中找到一个子集的和==target,那么另一半子集的和自然也就是target。
因此我们简化了这个问题,现在我们要做的是:
在这个集合中找出一个子集,使得子集的和等于target
但问题是使用回溯算法暴力搜索的话,就这道题而言,会超时。因此我们就要再想想还有没有别的方法
答案是有的。其实我们可以把他想为一个背包问题:一共有这么多的数,能否把容量为target的包满
那么不就是一个动态规划的问题嘛那么我们就开始动态规划的五步:
1.确定dp数组的含义以及下标含义:
dp[j] 容量为j的背包 能够容纳的最多价值为 dp[j],而这道题我们可以认为每一个元素的数值即是容量也是价值
如果我们把11这个背包装满之后,他的价值也是11,那么就说明存在一个子集,他的元素和为target
2.状态转移方程:dp[j]= max(dp[j] , dp[j-nums[i]]+nums[i[);
因此我们可以得到代码:
class Solution {
public:bool canPartition(vector<int>& nums) {int sum=0;vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {sum += nums[i];}if(sum%2==1){return false;}int target = sum/2;for(int i=0;i<nums.size();i++){for(int j=target;j>=nums[i];j--){dp[j]= max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[target]==target){return true;}else{return false;}}
};总结
动态规划的题目更加灵活多变,有的时候很难想出来这还能用动态规划的思路来做,因此我们要多做多练,才可以学好动态规划。
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!

相关文章:

【力扣刷题 | 第二十四天】
目录 前言: 416. 分割等和子集 - 力扣(LeetCode) 总结 前言: 今晚我们爆刷动态规划类型的题目。 416. 分割等和子集 - 力扣(LeetCode) 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这…...
(常用库))
PyTorch使用(一)(常用库)
1.各大模型库 hub:简单来说就是专门为PyTorch集成的算法模型库 网站:GitHub - pytorch/hub: Submission to https://pytorch.org/hub/ Model Zoo:这个平台上提供预训练模型,在每个模型上,会标注出这个模型在GitHub的标…...

React ~ React Router 6
React Router 6 VS React Router 5.x 内置组件的变化; 移除<Switch /> , 新增<Routes />语法的变化; component { About } 变为 element { <About /> }新增多个hook官方明确推荐函数式组件了! 一级路由(变化) 安装路由 npm i react-router-dom (默认是最…...
【LeetCode每日一题】——304.二维区域和检索-矩阵不可变
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 矩阵 二【题目难度】 中等 三【题目编号】 304.二维区域和检索-矩阵不可变 四【题目描述】 …...
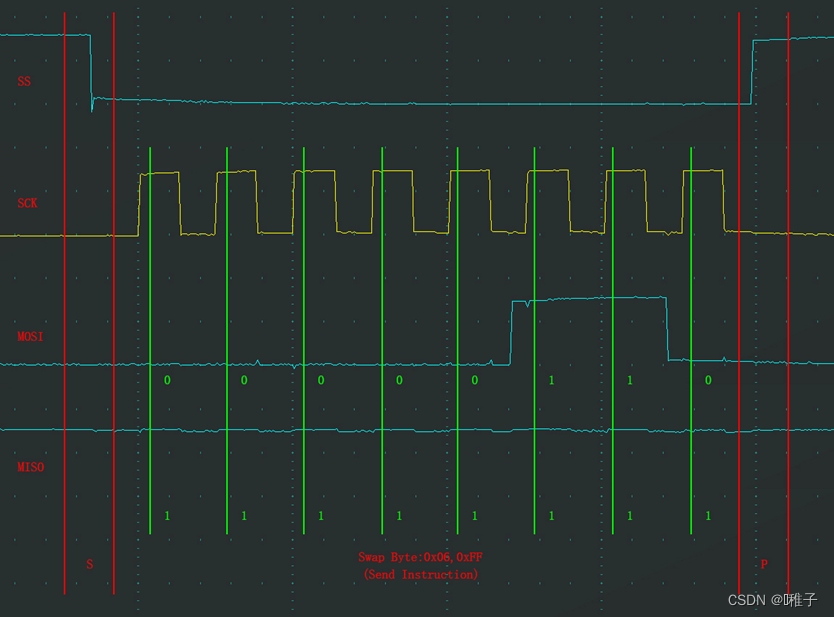
硬件串口通信协议学习(UART、IIC、SPI、CAN)
0.前言 学习资料:江协科技的个人空间-江协科技个人主页-哔哩哔哩视频 通信的目的:将一个设备的数据传送到另一个设备,扩展硬件系统通信协议:制定通信的规则,通信双方按照协议规则进行数据收发 全双工:通信…...

第一章-JavaScript基础进阶part2:事件
文章目录 概念一、注册事件(绑定事件)1.1 addEventListener事件监听 二、删除事件(解绑)三、DOM事件流四、事件对象event4.1 e.target与this与e.currentTarget的区别4.2 事件对象的常见属性 五、阻止事件默认行为及冒泡六、事件委…...

如何优雅的使用后端接口
优雅的后端接口 一个后端接口大致分为四个部分:接口地址(url)、接口请求方式(get、post等)、请求数据(request)、响 应数据(response)。 一、URL & Method Rest 设计风格 》 Restful API 简单理解: URI 是用来唯一标志一个互联网资源;Me…...
)
QEMU源码全解析25 —— QOM介绍(14)
接前一篇文章:QEMU源码全解析24 —— QOM介绍(13) 本文内容参考: 《趣谈Linux操作系统》 —— 刘超,极客时间 《QEMU/KVM》源码解析与应用 —— 李强,机械工业出版社 特此致谢! 本文开始对于…...

TopK问题
topK问题: N个数找最大或者最小的前k个。 例子: 优质筛选(店面的排名) 10000个数,找出最大的前10个数 解决思路:建立大堆,然后pop9次 但是有些场景,上面的思路…...
接口自动化测试-Postman+Newman+Git+Jenkins实战集成(详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Postman 创建…...
)
CMake 学习笔记 (Generator Expressions)
CMake 学习笔记 (Generator Expressions) Generator Expressions 可以认为是一种特殊的变量,它会在编译阶段求值。通常用在 target_link_libraries(), target_include_directories(), target_compile_definitions() 上。 用 Generator Expr…...
提高测试用例质量的6大注意事项
在软件测试中,经常会遇到测试用例设计不完整,用例没有完全覆盖需求等问题,这样往往容易造成测试工作效率低下,不能及时发现项目问题,无形中增加了项目风险。 因此提高测试用例质量,就显得尤为重要。一般来说…...

2023牛客暑期多校训练营6 A-Tree (kruskal重构树))
文章目录 题目大意题解参考代码 题目大意 ( 0 ≤ a i ≤ 1 ) , ( 1 ≤ c o s t i ≤ 1 0 9 ) (0\leq a_i\leq 1),(1 \leq cost_i\leq 10^9) (0≤ai≤1),(1≤costi≤109) 题解 提供一种新的算法,kruskal重构树。 该算法重新构树,按边权排序每一条边…...
软件测试—支付功能测试
有人问过我这样一个问题:作为一个支付平台,接入了快钱、易宝或直连银行等多家的渠道,内在的产品流程是自己的。业内有什么比较好的测试办法,来测试各渠道及其支持的银行通道呢? 回答:对支付平台而言&#…...

自动化测试的统筹规划
背景 回顾以前自动化测试编写的经历,主要是以开发者自驱动的方式进行,测试的编写随心而动,没有规划,也没有章法,这样就面临如下的一些问题: 测试用例设计不到位,覆盖不全,或者不够…...
、django中如何开启事务)
外键字段的增删改查、多表查询(子查询和连表查询、正反向、聚合查询、 分组查询、 F与Q查询)、django中如何开启事务
一、 外键字段的增删改查 1.多对多的外键增删改查图书和作者是多对多,借助于第三张表实现的,如果想绑定图书和作者的关系,本质上就是在操作第三方表2.如何操作第三张表问题:让你给图书添加一个作者,他俩的关系可是多对…...
【学习笔记】生成式AI(ChatGPT原理,大型语言模型)
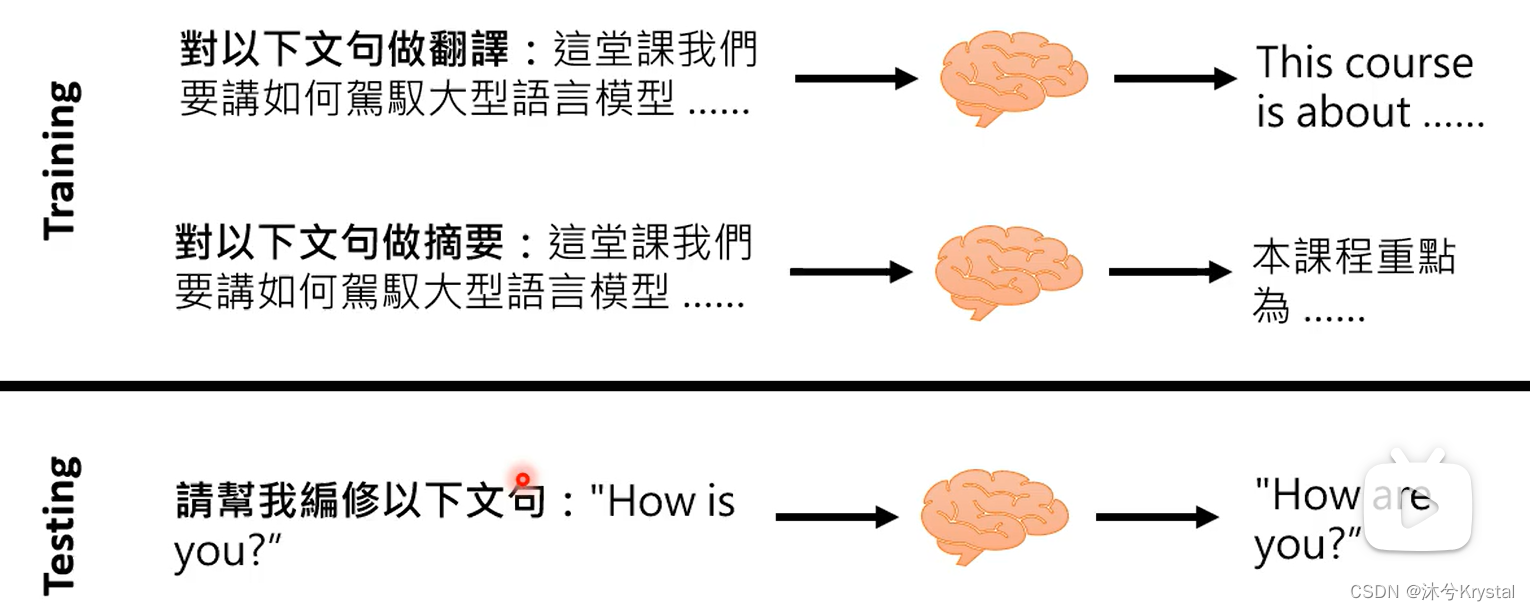
ChatGPT原理剖析 语言模型 文字接龙 ChatGPT在测试阶段是不联网的。 ChatGPT背后的关键技术:预训练(Pre-train) 又叫自监督式学习(Self-supervised Learning),得到的模型叫做基石模型(Founda…...

【Opencv入门到项目实战】(三):图像腐蚀与膨胀操作
文章目录 1.腐蚀操作2.膨胀操作3.开运算和闭运算4.礼帽与黑帽5.梯度运算 1.腐蚀操作 腐蚀操作是图像处理中常用的一种形态学操作,我们通常用于去除图像中的噪声、分割连通区域、减小目标物体的尺寸等。腐蚀操作的原理是,在给定的结构元素下,…...
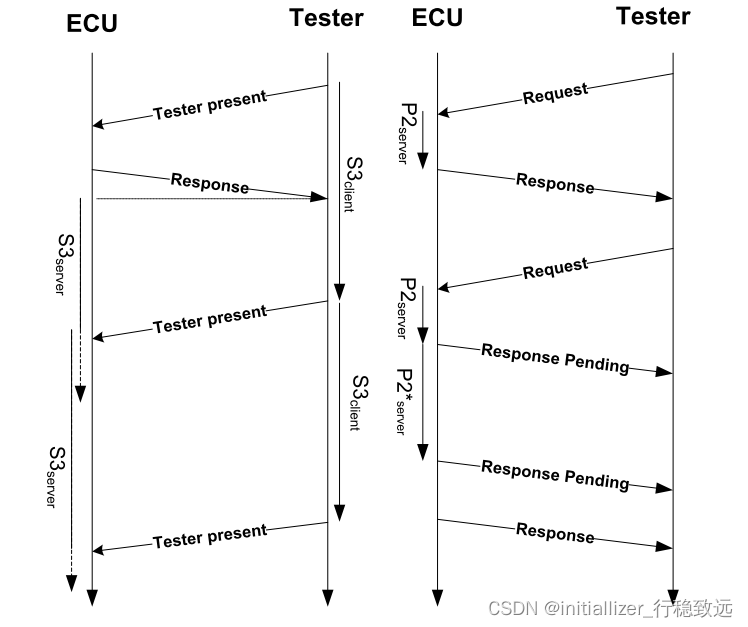
Autosar诊断系列介绍20 - UDS应用层P2Server/P2Client等时间参数解析
本文框架 1. 前言2.几个时间参数含义2.1 P2Client与P2Server2.2 P2*Client与P2*Server2.3 P3Client_Phys与P3Client_Func2.4 S3Client与S3Server 1. 前言 本系列Autosar 诊断入门介绍,会详细介绍诊断相关基础知识,如您对诊断实战有更高需求,…...
【iOS】json数据解析以及简单的网络数据请求
文章目录 前言一、json数据解析二、简单的网络数据请求三、实现访问API得到网络数据总结 前言 近期写完了暑假最后一个任务——天气预报,在里面用到了简单的网络数据请求以及json数据的解析,特此记录博客总结 一、json数据解析 JSON是一种轻量级的数据…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...
)
window 显示驱动开发-如何查询视频处理功能(三)
D3DDDICAPS_GETPROCAMPRANGE请求类型 UMD 返回指向 DXVADDI_VALUERANGE 结构的指针,该结构包含特定视频流上特定 ProcAmp 控件属性允许的值范围。 Direct3D 运行时在D3DDDIARG_GETCAPS的 pInfo 成员指向的变量中为特定视频流的 ProcAmp 控件属性指定DXVADDI_QUER…...

VUE3 ref 和 useTemplateRef
使用ref来绑定和获取 页面 <headerNav ref"headerNavRef"></headerNav><div click"showRef" ref"buttonRef">refbutton</div>使用ref方法const后面的命名需要跟页面的ref值一样 const buttonRef ref(buttonRef) cons…...
