通信原理复习公式整理(自用/持续更新)
目录
- 符号表
- 欧拉公式
- 第一章
- 平均信息量
- 传信率(信息速率)
- 传码率(码元速率)
- 第二章
- 第三章
- 第四章
- 第五章
- 第六章 数字信号的载波传输
- 2ASK带宽
- 余弦滚降基带信号-2ASK带宽
- 2FSK带宽
- 余弦滚降基带信号-2ASK带宽
- 2PSK带宽
- 匹配滤波器最大输出信噪比
- 最佳线性滤波器传输特性
- ASK系统信号能量
- FSK系统信号能量
- 二进制最佳接收信噪比
- 多进制绝对相移MPSK带宽
- 余弦滚降基带信号-MPSK带宽
参考书:现代通信原理(第二版) 沈保锁 侯春萍 等编著
注意:有的公式并不是所有的情况都满足,这里只给出书上还有我自己总结的公式,用之前要想一想能否适用
符号表
| 符号 | 含义 |
|---|---|
| τ \tau τ | 脉冲宽度 |
| T s T_s Ts | 码元宽度 |
欧拉公式
e j x = c o s ( x ) + j s i n ( x ) e^{jx}=cos(x)+jsin(x) ejx=cos(x)+jsin(x)
第一章
平均信息量
H ( x ) = P ( x 1 ) l o g 2 1 P ( x 1 ) + P ( x 2 ) l o g 2 1 P ( x 2 ) + . . . + P ( x n ) l o g 2 1 P ( x n ) = − ∑ n i = 1 P ( x i ) l o g 2 1 P ( x i ) (比特 / 符号) H(x)=P(x_1)log_{2}\frac{1}{P(x_1)} +P(x_2)log_{2}\frac{1}{P(x_2)}+...+P(x_n)log_{2}\frac{1}{P(x_n)}\\=-\sum_{n}^{i=1}P(x_i)log_{2}\frac{1}{P(x_i)} (比特/符号) H(x)=P(x1)log2P(x1)1+P(x2)log2P(x2)1+...+P(xn)log2P(xn)1=−n∑i=1P(xi)log2P(xi)1(比特/符号)
传信率(信息速率)
R b = R B l o g 2 N = 1 T s ( b / s ) R_b=R_Blog_{2}N=\frac{1}{T_s} (b/s) Rb=RBlog2N=Ts1(b/s)
N为进制数
传码率(码元速率)
R B = R b l o g 2 N ( B , 波特) R_B=\frac{R_b}{log_2N}(B,波特) RB=log2NRb(B,波特)
Ts为码元持续时间
第二章
第三章
第四章
第五章
第六章 数字信号的载波传输
2ASK带宽
B 2 A S K = 2 f s = 2 T s B_{2ASK}=2f_{s}=\frac{2}{T_{s}} B2ASK=2fs=Ts2
余弦滚降基带信号-2ASK带宽
B 2 A S K = 2 B = ( α + 1 ) f s = α + 1 T s B_{2ASK}=2B=(\alpha +1)f_{s}=\frac{\alpha +1}{T_{s}} B2ASK=2B=(α+1)fs=Tsα+1
B为基带信号带宽
2FSK带宽
B F S K = ∣ f 2 − f 1 ∣ + 2 f s B_{FSK}=\left |f_{2}-f_{1} \right | +2f_{s} BFSK=∣f2−f1∣+2fs
余弦滚降基带信号-2ASK带宽
B F S K = ∣ f 2 − f 1 ∣ + ( α + 1 ) f s B_{FSK}=\left |f_{2}-f_{1} \right | +(\alpha +1)f_{s} BFSK=∣f2−f1∣+(α+1)fs
2PSK带宽
B P S K = 2 f s = 2 T s B_{PSK}=2f_{s}=\frac{2}{T_{s}} BPSK=2fs=Ts2
匹配滤波器最大输出信噪比
r o m a x = 2 E n 0 r_{omax}=\frac{2E}{n_0} romax=n02E
n0是单边带噪声功率谱密度
最佳线性滤波器传输特性
H ( ω ) = K ⋅ S ∗ ( ω ) e − j ω t 0 H(\omega )=K \cdot S^{\ast }(\omega )e^{-j\omega t_{0}} H(ω)=K⋅S∗(ω)e−jωt0
ASK系统信号能量
E 1 = A 2 T 2 = E E_1=\frac{A^2T}{2}=E E1=2A2T=E
FSK系统信号能量
E 1 = E 2 = A 2 T s 2 E_1=E_2=\frac{A^2T_s}{2} E1=E2=2A2Ts
二进制最佳接收信噪比
S N = E b R b n 0 B \frac{S}{N} =\frac{E_bR_b}{n_0B} NS=n0BEbRb
多进制绝对相移MPSK带宽
B M P S K = 2 f s = 2 T s B_{MPSK}=2f_{s}=\frac{2}{T_{s}} BMPSK=2fs=Ts2
余弦滚降基带信号-MPSK带宽
相关文章:
)
通信原理复习公式整理(自用/持续更新)
目录 符号表欧拉公式第一章平均信息量传信率(信息速率)传码率(码元速率) 第二章第三章第四章第五章第六章 数字信号的载波传输2ASK带宽余弦滚降基带信号-2ASK带宽2FSK带宽余弦滚降基带信号-2ASK带宽2PSK带宽匹配滤波器最大输出信噪比最佳线性滤波器传输特性ASK系统信号能量FSK系…...

TypeScript实战篇 - TS实战: 服务层开发 - 完整的聊天服务
目录 huatian-svc/src/main.ts huatian-svc/src/context/ChatContext.ts huatian-svc/src/ChatSession.ts huatian-svc/src/service/ChatIDService.ts huatian-svc/src/dao/DB.ts huatian-svc/src/dao/Dao.ts huatian-svc/src/dao/create_db.ts huatian-svc/src/main.ts…...
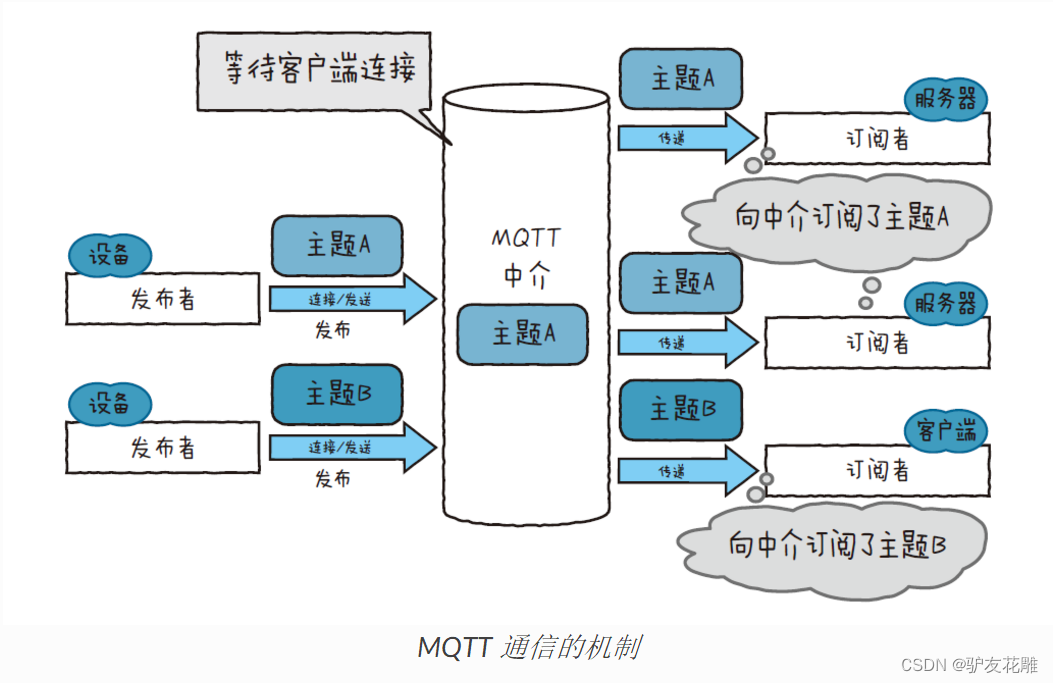
【雕爷学编程】MicroPython动手做(32)——物联网之MQTT
MQTT (Message Queuing Telemetry Transport)消息队列遥测传输协议,是一种基于发布/订阅(publish/subscribe)模式的"轻量级"通讯协议,该协议构建于TCP/IP协议上,由IBM在1999年发布。M…...
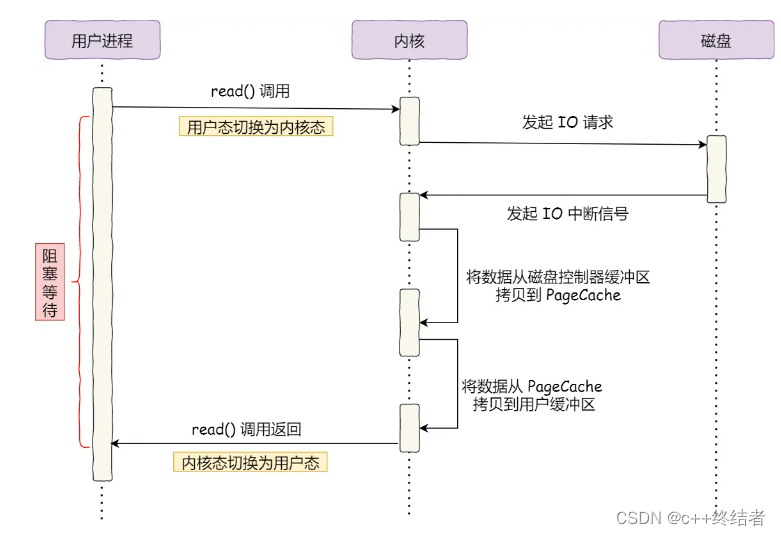
操作系统专栏4-网络专题from小林coding
网络专题 文件传输mmapwritesend file大文件传输过程 文件传输 传统的文件传输过程 在这个过程中发生了4次用户态与内核态之间的切换,4次数据拷贝分别是 read系统调用陷入内核,read完成返回write调用陷入内核,write返回 4次数据拷贝分别是 磁盘->内核缓冲区->用户缓冲…...
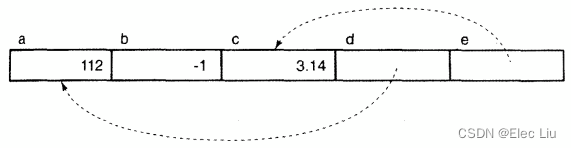
《C和指针》(6)指针
1、内存和地址 计算机的内存是由数以亿万计的位(bit)组成,每一个位可以容纳值0、1值。由于一个位所能表示的值的范围太有限,所以单独的位用处不大。通常许多为合成一组作为一个单位,这样就可以存储范围较大的值。下图…...

零基础强化学习入门分享
(一)前言:强化学习入门顺序。 以前主要学习硬件PCB单片机等知识,后来接触的项目也大多与电气相关,从一窍不通到稍微找到点门道,中间走过不少弯路,误打误撞中,也留下了一些经验。 我的…...

QT快捷键
--------------------------------------------------- --------------------------------------------------- QT断点调试 Ctrl B 编译程序 F5 调试运行程序 F10 单步调试 F11 进入函数调试 --------------------------------------------------- -----------------------…...
LabVIEW 开发在不确定路况下自动速度辅助系统
LabVIEW 开发在不确定路况下自动速度辅助系统 智能驾驶辅助系统是汽车行业最先进的升级和尖端技术,智能交通系统依靠智能驾驶辅助系统在公共交通部门工作。该智能驾驶辅助系统技术包括自适应巡航控制,防抱死制动系统,安全气囊展开࿰…...

《面试1v1》ElasticSearch 和 Lucene
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...

P5727 【深基5.例3】冰雹猜想
【深基5.例3】冰雹猜想 题目描述 给出一个正整数 n n n,然后对这个数字一直进行下面的操作:如果这个数字是奇数,那么将其乘 3 3 3 再加 1 1 1,否则除以 2 2 2。经过若干次循环后,最终都会回到 1 1 1。经过验证很…...

ConcurrentHashMap1.7 源码浅析
分析过HashMap的1.7的版本的结构,但是HashMap是线程不安全的,多线程触发扩容还会发生死循环问题,那么ConcurrentHashMap 就是解决这个问题的,这是一个线程安全的Map,那么对应的内部实现是怎么样的,简单分析…...

跨境电商时代的安全护航
随着跨境电商业务的蓬勃发展,网络安全问题日益突出。为了保障个人信息的安全和商业竞争的公平性,防关联浏览器和多开浏览器的需求日益增长。本文将为您介绍隐擎fox指纹浏览器,探讨其在跨境电商时代的重要作用,以及如何通过该浏览器…...

JavaScript Es6 _1 笔记
JavaScript Es6 _1 笔记 学习作用域、变量提升、闭包等语言特征,加深对 JavaScript 的理解,掌握变量赋值、函数声明的简洁语法,降低代码的冗余度。 理解作用域对程序执行的影响能够分析程序执行的作用域范围理解闭包本质,利用闭包…...

结构体和 Json 相互转换(序列化反序列化)
关于 JSON 数据 JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式。易于人阅读和编写。同时也 易于机器解析和生成。RESTfull Api 接口中返回的数据都是 json 数据。 Json 的基本格式如下: { "a": "Hello", "b": "…...

【力扣刷题 | 第二十四天】
目录 前言: 416. 分割等和子集 - 力扣(LeetCode) 总结 前言: 今晚我们爆刷动态规划类型的题目。 416. 分割等和子集 - 力扣(LeetCode) 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这…...
(常用库))
PyTorch使用(一)(常用库)
1.各大模型库 hub:简单来说就是专门为PyTorch集成的算法模型库 网站:GitHub - pytorch/hub: Submission to https://pytorch.org/hub/ Model Zoo:这个平台上提供预训练模型,在每个模型上,会标注出这个模型在GitHub的标…...

React ~ React Router 6
React Router 6 VS React Router 5.x 内置组件的变化; 移除<Switch /> , 新增<Routes />语法的变化; component { About } 变为 element { <About /> }新增多个hook官方明确推荐函数式组件了! 一级路由(变化) 安装路由 npm i react-router-dom (默认是最…...
【LeetCode每日一题】——304.二维区域和检索-矩阵不可变
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 矩阵 二【题目难度】 中等 三【题目编号】 304.二维区域和检索-矩阵不可变 四【题目描述】 …...
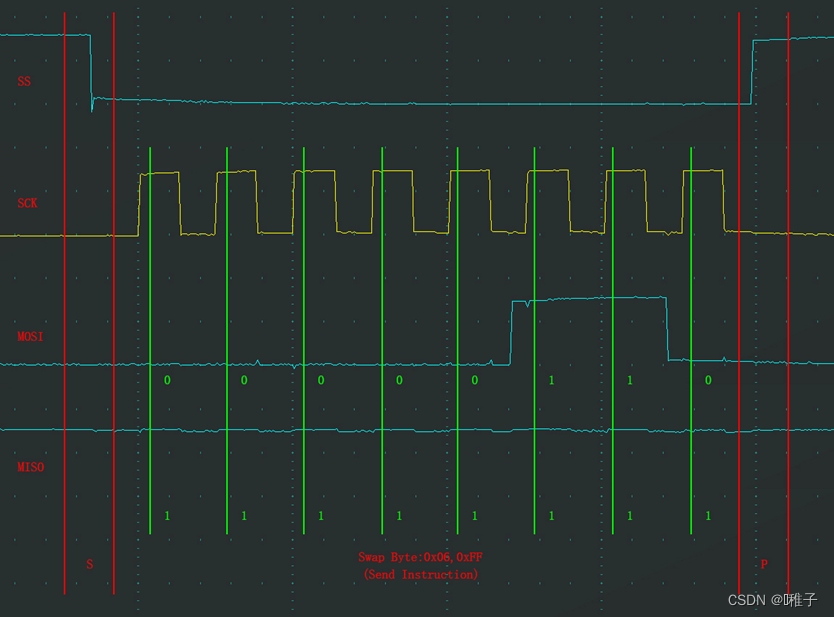
硬件串口通信协议学习(UART、IIC、SPI、CAN)
0.前言 学习资料:江协科技的个人空间-江协科技个人主页-哔哩哔哩视频 通信的目的:将一个设备的数据传送到另一个设备,扩展硬件系统通信协议:制定通信的规则,通信双方按照协议规则进行数据收发 全双工:通信…...

第一章-JavaScript基础进阶part2:事件
文章目录 概念一、注册事件(绑定事件)1.1 addEventListener事件监听 二、删除事件(解绑)三、DOM事件流四、事件对象event4.1 e.target与this与e.currentTarget的区别4.2 事件对象的常见属性 五、阻止事件默认行为及冒泡六、事件委…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
