C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig-zag/左右双旋/3+4重构)
目录
- 00.BBST——平衡二叉搜索树
- 01.AVL树
- 02.AVL的插入
- 2.1单旋——zig 与 zag
- 2.2插入节点后的单旋实例
- 2.3手玩小样例
- 2.4双旋实例
- 2.5小结
- 03.AVL的删除
- 3.1单旋删除
- 3.2双旋删除
- 3.3小结
- 04.3+4重构
- 05.综合评价AVL
- 5.1优点
- 5.2缺点
00.BBST——平衡二叉搜索树
本文是介绍众多平衡二叉搜索树(BBST)的第一篇——介绍AVL树。故先来引入BBST的概念。由于上一篇介绍的二叉搜索树(BST)在极度退化的情况下,十分不平衡,不平衡到只朝一侧偏,成为一条链表,复杂度可达 O ( n ) O(n) O(n),所以我们要在“平衡”方面做一些约束,以防我们的树结构退化得那么严重。
具体来说,含 n n n个节点,高度为 h h h的BST,若满足 h = O ( l o g 2 n ) h=O(log_2 n) h=O(log2n),则称为称为平衡二叉搜索树。
01.AVL树
AVL树是一种BBST(稍后会证明)。它约束自己是否平衡,主要靠一个指标——平衡因子。定义:平衡因子=左子树高度-右子树高度。如果满足 − 2 < 全部平衡因子 < 2 -2<全部平衡因子<2 −2<全部平衡因子<2,则该AVL树处于平衡状态;否则,需要靠一系列措施,将其恢复平衡。
首先先证明AVL树满足BBST的要求,即 h = O ( l o g 2 n ) h=O(log_2 n) h=O(log2n)(下式)。我们可转而证明n=Ω(Φh)(即,AVL的节点数不会太少)

结论:高度为h的AVL Tree 至少有 fib((h+3)-1 个节点
证明:



02.AVL的插入
插入一个节点会导致一串祖先的失衡,删除一个节点至多导致一个祖先失衡。但是,通过后续代码就可发现,删除节点比插入节点复杂的多。原因是,插入节点只要调整好了一处,这条路径上的所有祖先都可平衡,复杂度是
O(1)。而删除节点是,调整好了一处平衡,另一处就会不平衡,自下而上层层调整,复杂度是O(n)。
2.1单旋——zig 与 zag
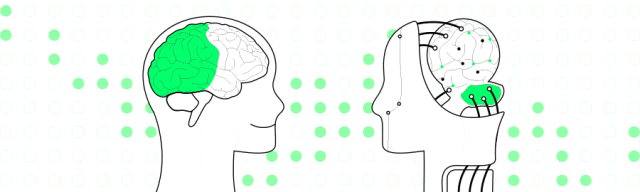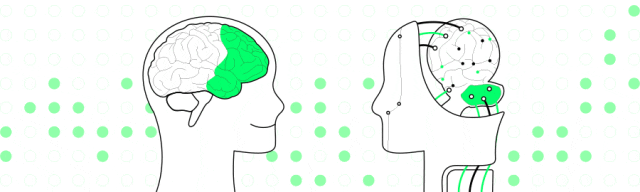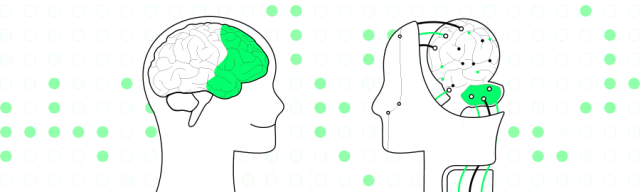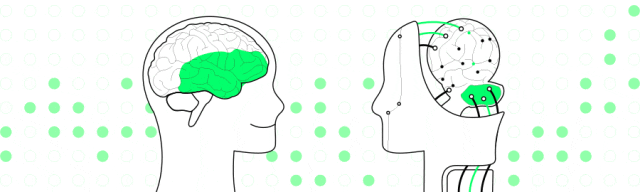
zig 与 zag 分别对应右单旋和左单旋。单旋的操作改变的是两个节点的相对位置。改变的是三条线:一上一下一子树。新树根上行指向原根,新树根原子树给到原根。如下图,V到Y那去,Y到C那去。

2.2插入节点后的单旋实例
在下图 处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈一条线,而非“之”字,所以用单旋调整(之字形对应双旋)。具体来说,对g左单旋。
处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈一条线,而非“之”字,所以用单旋调整(之字形对应双旋)。具体来说,对g左单旋。
2.3手玩小样例
例题:将1,2,3,4,5,6依次插入空的AVL Tree,最终AVL Tree长成什么样?
过程:
首先正常插入1,2;插入3时,1是第一个发现不平衡的节点,zag(1),即对1进行左单旋,成功解决;正常插入4

插入5时,3是第一个发现不平衡的节点,zag(3),即对3进行左单旋,成功解决

插入6时,2是第一个发现不平衡的节点,zag(2),即对2进行左单旋,成功解决

2.4双旋实例
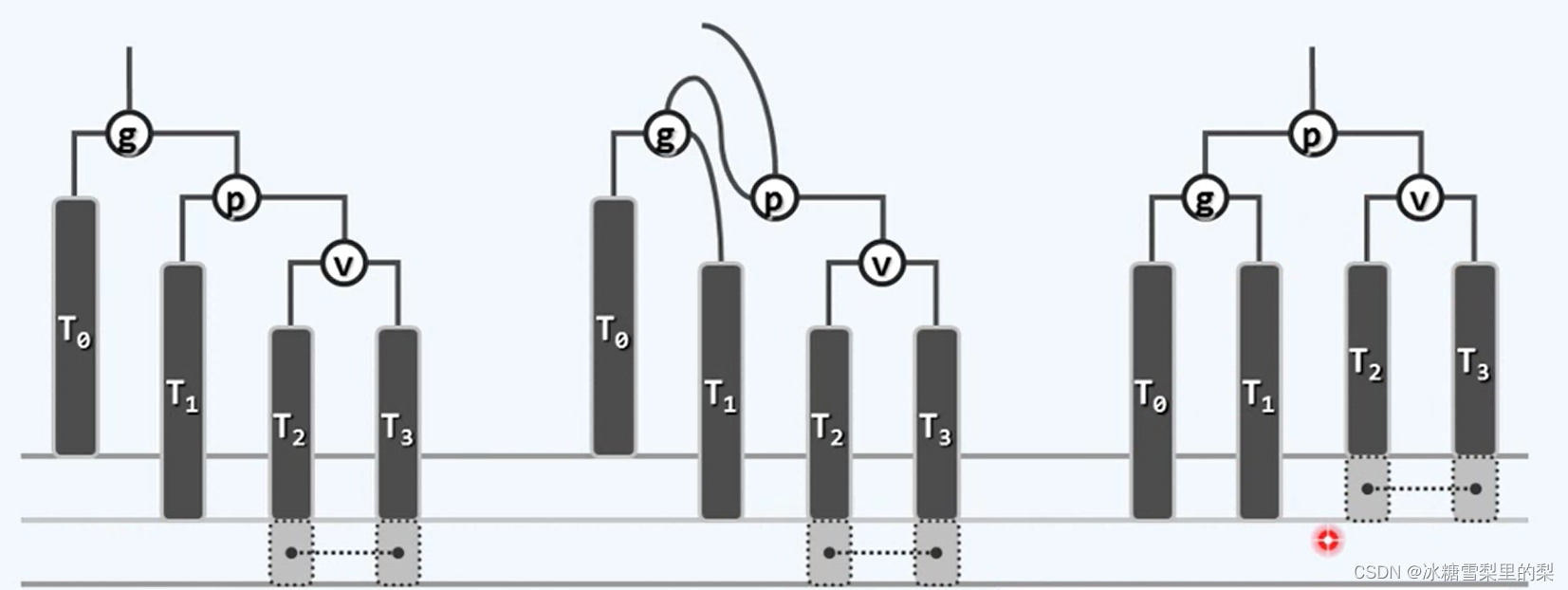
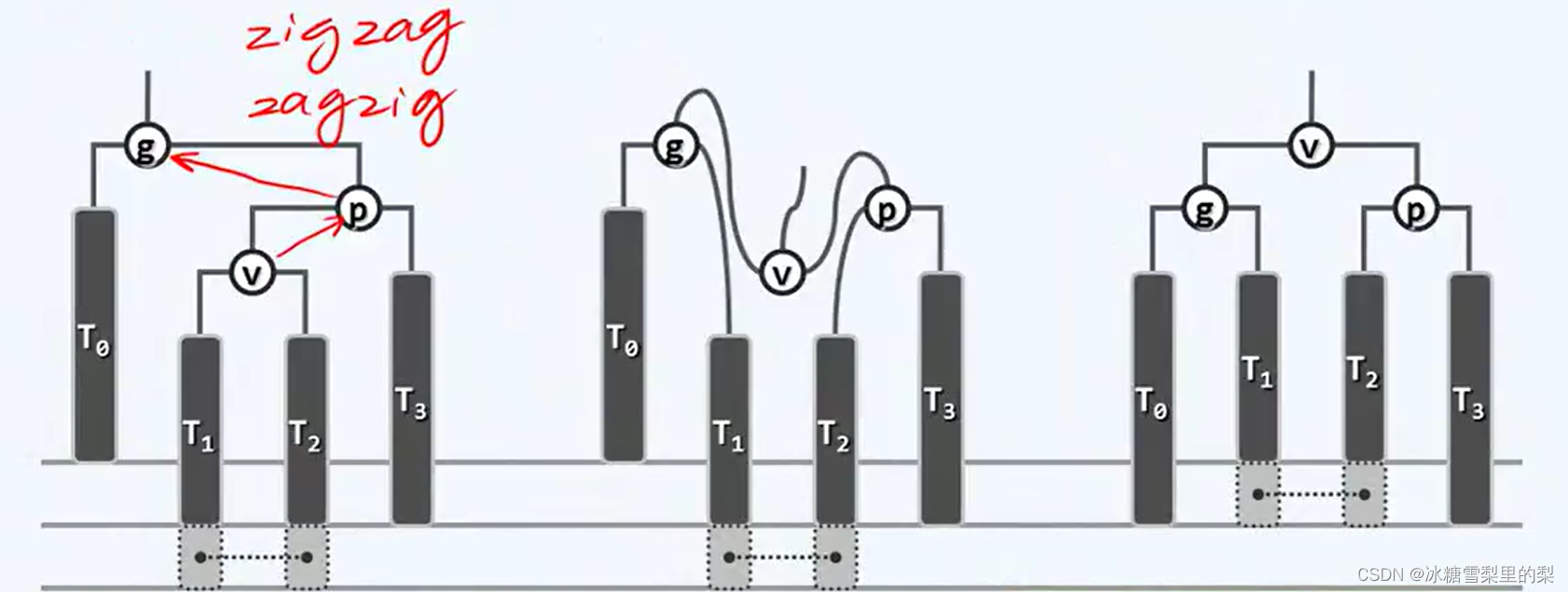
双旋的操作改变的是三个节点的相对位置。分为两种情况——zig-zag与zag-zig。
在下图 处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈“之”字,所以用双旋。具体来说,先zig§,再zag(g).
处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈“之”字,所以用双旋。具体来说,先zig§,再zag(g).
2.5小结
AVL树中插入节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度是不变的,子树高度复原,更高祖先也必平衡,全树复衡。故在AVL树中修正插入节点引发的失衡不会出现失衡传播。
03.AVL的删除
删除一个节点至多导致一个祖先失衡。
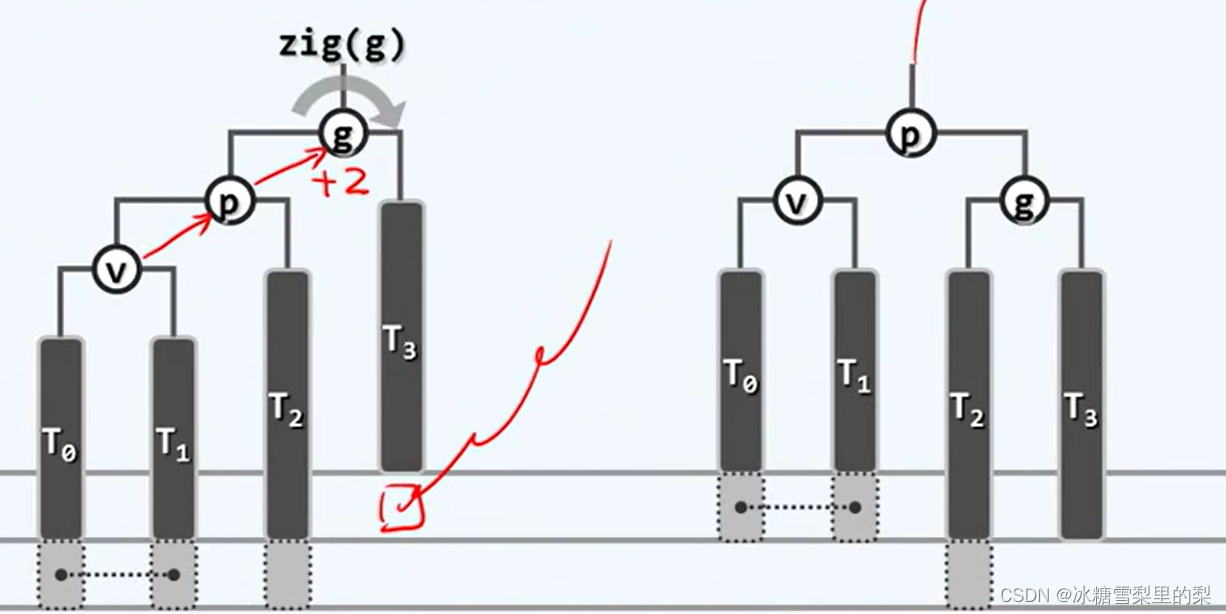
3.1单旋删除
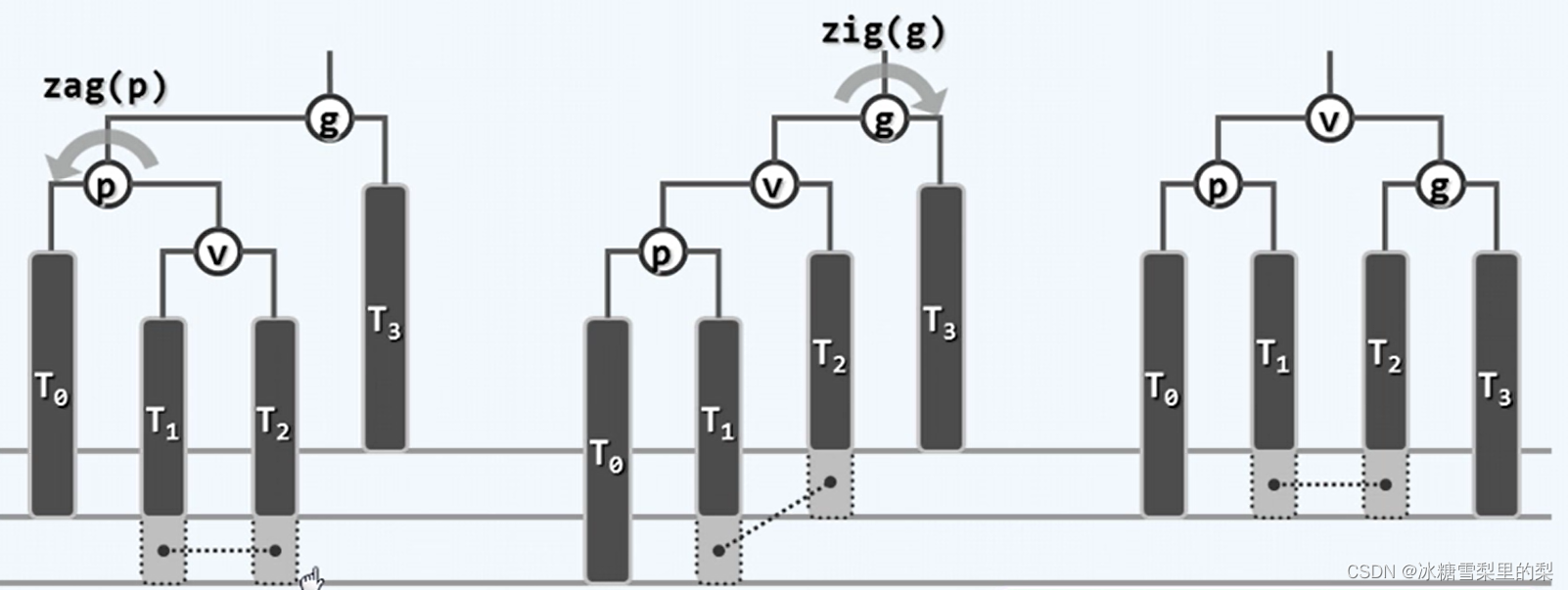
3.2双旋删除
3.3小结
AVL树中删除节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度有可能不变也有可能减小1,故在AVL树中修正删除节点引发的失衡有可能出现失衡传播。
04.3+4重构
通过观察以上插入和删除的结果示意图,发现结构是一样的——三个节点按顺序呈三角形,四个子树按原来的顺序分别挂在两个孩子节点的下边。(如下图)

那我们就不必关注具体的技巧了,而是将三个节点和四个子树拆开,像暴力组装魔方那样(先拆散)拼上。
05.综合评价AVL
5.1优点
- 查找、插入、删除,最坏时间复杂度为 O ( l o g n ) O(logn) O(logn)
- O ( n ) O(n) O(n)的存储空间
5.2缺点
- 需要额外维护高度或平衡因子这一指标(后续Splay Tree可改善这一问题)
- 删除操作后,最多需旋转 Ω ( l o g n ) \Omega(logn) Ω(logn)次
- 单次动态调整后,全树拓扑结构的变化量可能高达 Ω ( l o g n ) \Omega(logn) Ω(logn) (RedBlack Tree可缩到 O ( 1 ) O(1) O(1))
谢谢观看~
相关文章:

C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig-zag/左右双旋/3+4重构)
目录 00.BBST——平衡二叉搜索树01.AVL树02.AVL的插入2.1单旋——zig 与 zag2.2插入节点后的单旋实例2.3手玩小样例2.4双旋实例2.5小结 03.AVL的删除3.1单旋删除3.2双旋删除3.3小结 04.34重构05.综合评价AVL5.1优点5.2缺点 00.BBST——平衡二叉搜索树 本文是介绍众多平衡二叉搜…...
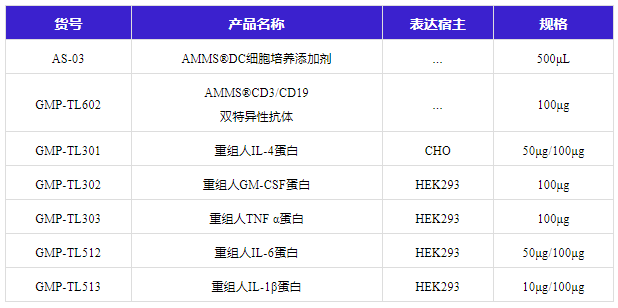
免疫疗法勘察兵——DC细胞
DC细胞又叫树状细胞或者树突细胞,1869年由保罗兰格尔翰斯发现,一开始被误以为是神经细胞的一种,直到1973年皮肤科医师Inga Silberberg发现了他的免疫功能,同年,被拉尔夫斯坦曼和赞威尔A科恩两人正式命名为“dendritic…...
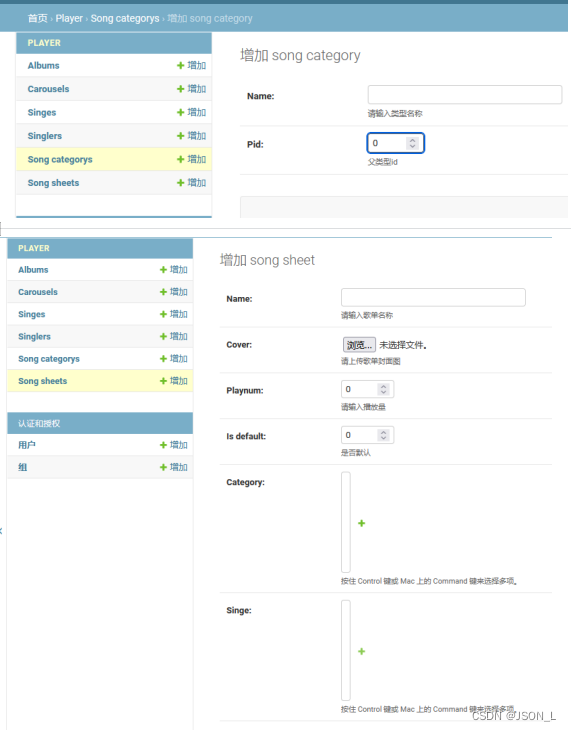
Django实现音乐网站 ⑷
使用Python Django框架制作一个音乐网站,在系列文章3的基础上继续开发, 本篇主要是后台歌曲类型表、歌单表模块功能开发。 目录 表结构设计 歌曲类型表结构 歌单表结构 创建表模型 创建表 后台注册表模型 引入表模型 后台自定义 总结 表结构设计…...
2023年华数杯数学建模C题思路 - 母亲身心健康对婴儿成长的影响
# 1 赛题 C 题 母亲身心健康对婴儿成长的影响 母亲是婴儿生命中最重要的人之一,她不仅为婴儿提供营养物质和身体保护, 还为婴儿提供情感支持和安全感。母亲心理健康状态的不良状况,如抑郁、焦虑、 压力等,可能会对婴儿的认知、情…...

openGauss学习笔记-30 openGauss 高级数据管理-别名
文章目录 openGauss学习笔记-30 openGauss 高级数据管理-别名30.1 语法格式30.1.1 列别名语法30.1.2 表别名语法 30.2 参数说明30.3 示例 openGauss学习笔记-30 openGauss 高级数据管理-别名 SQL可以重命名一张表或者一个字段的名称,这个名称为该表或该字段的别名。…...

C#实现多线程局域网扫描器的思路与具体代码
C#实现多线程局域网扫描器的思路与具体代码 思路: 获取局域网内所有 IP 地址遍历所有 IP 地址,使用 Ping 命令测试主机是否在线如果主机在线,则扫描主机上的所有端口,确定哪些端口是开放的输出扫描结果 在上述过程中࿰…...
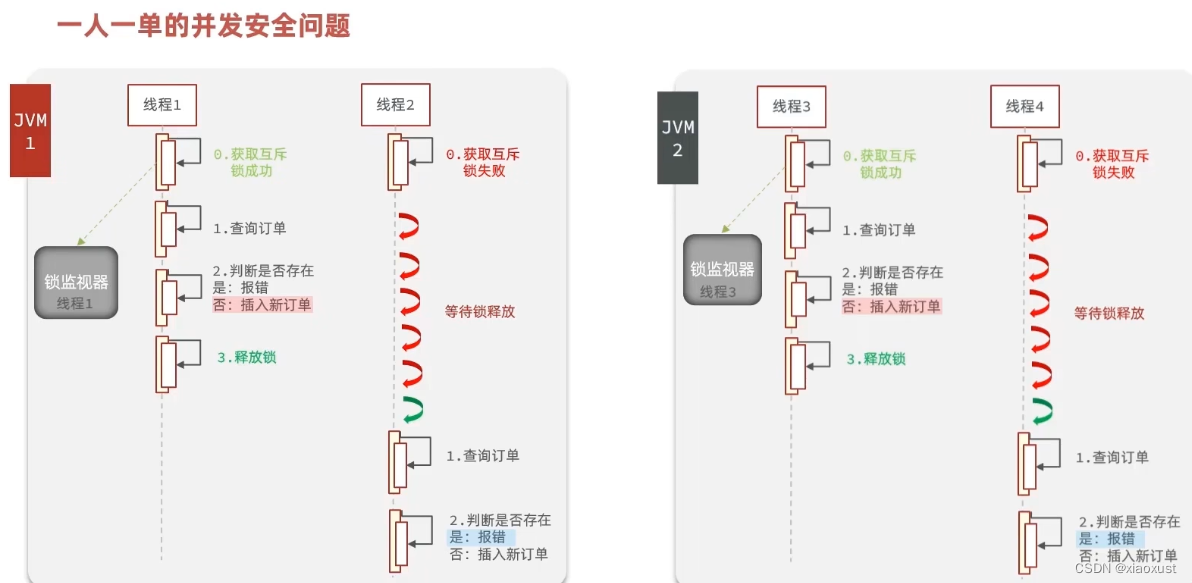
Redis秒杀:一人一单问题及初步解决
优惠券秒杀一人一单 前言一、需求以及之前存在的问题二、增加一人一单逻辑1.初步代码2.封装一人一单逻辑3.控制锁的粒度 三、事务控制问题四、总结 前言 跟随黑马虎哥学习redis: 这是我认为b站上最好的redis教程,各方面讲解透彻,知识点覆盖…...
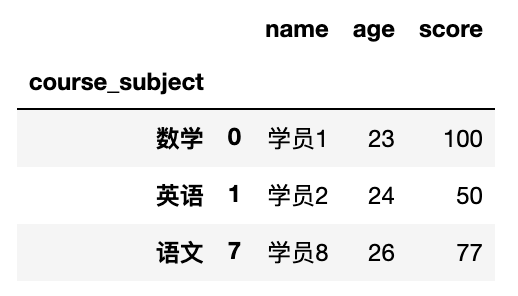
python 数据分析面试题:求分组排第n名的记录数据
近期面试遇到一个面试题,分享给大家。 文中会提供详细的解题思路以及问题延伸 一、面试题 面试题:输出各学科总分第一名的学员姓名、年龄、分数数据: class_a {name: [学员1, 学员2, 学员3, 学员4,学员5],age: [23, 24, 26, 27,25],course…...

eclipse常用快捷键
Eclipse常用快捷键 补全代码的声明:alt /快速修复: ctrl 1批量导包:ctrl shift o使用单行注释:ctrl /使用多行注释: ctrl shift /取消多行注释:ctrl shift \复制指定行的代码:ctrl alt down 或…...

什么是OCR?OCR技术详解
光学字符识别(Optical Character Recognition)简称为“OCR”。ORC是指对包含文本资料的图像文件进行分析识别处理,获取文字及版面信息的技术。 一般包括以下几个过程: 1.图像输入 针对不同格式的图像,有着不同的存储格式和压缩方式。目前&…...
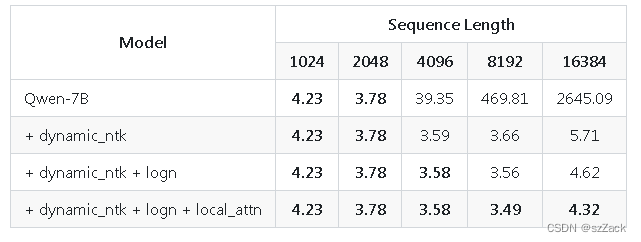
【大模型】开源且可商用的大模型通义千问-7B(Qwen-7B)来了
【大模型】开源且可商用的大模型通义千问-7B(Qwen-7B)来了 新闻通义千问 - 7B 介绍评测表现快速使用环境要求安装相关的依赖库推荐安装flash-attention来提高你的运行效率以及降低显存占用使用 Transformers 运行模型使用 ModelScope 运行模型 量化长文本…...

SQL分类及通用语法数据类型
一、SQL分类 DDL: 数据定义语言,用来定义数据库对象(数据库、表、字段)DML: 数据操作语言,用来对数据库表中的数据进行增删改DQL: 数据查询语言,用来查询数据库中表的记录DCL: 数据控制语言,用来创建数据库…...

亿欧智库:2023中国功效型护肤产品成分解析研究报告(附下载
关于报告的所有内容,公众【营销人星球】获取下载查看 核心观点 消费端:“纯净美妆〞概念火热,消费驱动因素向成分来源硬核转变 新冠疫情过后,消费者对于生活健康:自然,可持续的关注度持续上升。在消费者…...
主机准备和负载均衡器安装)
Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...

python与深度学习(十二):CNN和猫狗大战二
目录 1. 说明2. 猫狗大战的CNN模型测试2.1 导入相关库2.2 加载模型2.3 设置保存图片的路径2.4 加载图片2.5 图片预处理2.6 对图片进行预测2.7 显示图片 3. 完整代码和显示结果4. 多张图片进行测试的完整代码以及结果 1. 说明 本篇文章是对上篇文章猫狗大战训练的模型进行测试。…...

React(1)——快速入门
目录 一、React背景简介 ❤️ 官网和资料 📚 介绍描述 🐧 React的特点 🔨 React高效的原因 🙏🏻 二、React的基本使用 💻 三、React JSX(JSX:JavaScript XML)📦 …...
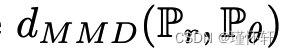
【论文】【生成对抗网络五】Wasserstein GAN (WGAN)
【题目、作者】: 紫色:要解决的问题或发现的问题 红色:重点内容 棕色:关联知识,名称 绿色:了解内容,说明内容 论文地址: 论文下载 本篇文章仅为原文翻译,仅作参考。…...
)
学习率Learn_rate是什么(深度学习)
学习率是指在训练神经网络时用于调整参数的步进大小,它决定了每次梯度更新时参数的调整程度。学习率的选择直接关系到模型的性能和训练过程的效果。 学习率变化可能带来的影响: 收敛速度:较高的学习率可以加快模型的收敛速度,因为…...
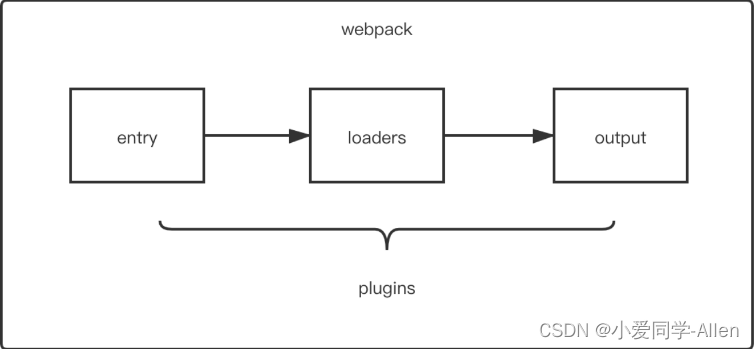
webpack基础知识五:说说Loader和Plugin的区别?编写Loader,Plugin的思路?
一、区别 前面两节我们有提到Loader与Plugin对应的概念,先来回顾下 loader 是文件加载器,能够加载资源文件,并对这些文件进行一些处理,诸如编译、压缩等,最终一起打包到指定的文件中plugin 赋予了 webpack 各种灵活的…...
AI大模型之花,绽放在鸿蒙沃土
随着生成式AI日益火爆,大语言模型能力引发了越来越多对于智慧语音助手的期待。 我们相信,AI大模型能力加持下的智慧语音助手一定会很快落地,这个预判不仅来自对AI大模型的观察,更来自对鸿蒙的了解。鸿蒙一定会很快升级大模型能力&…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
