21. 合并两个有序链表
题目链接:
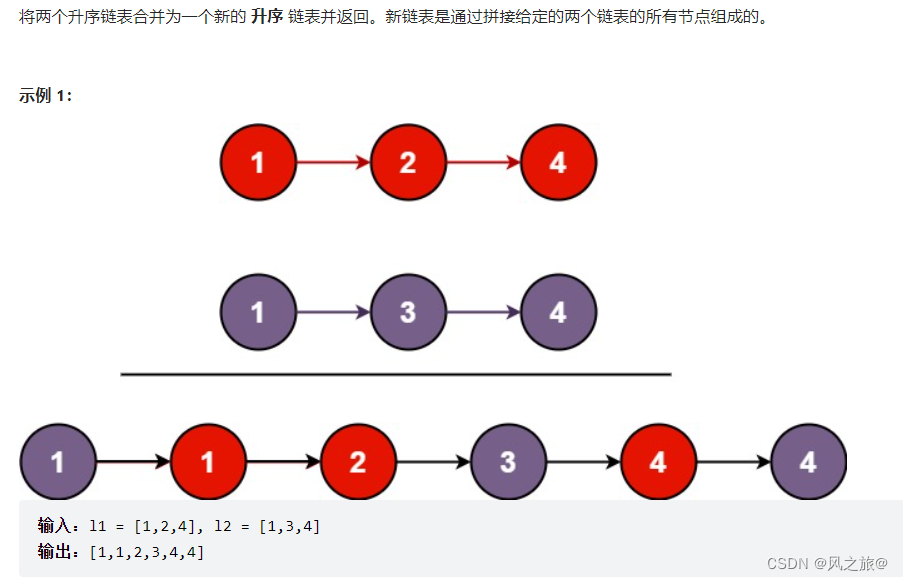
解题思路:
遍历,双指针:因为两个链表有序,所以只需要依次比较两个元素的大小,然后添加到新的链表中即可
first指针指向第一个链表l1,second指针指向第二个链表l2,answer保存合并后的链表的头节点的前驱,prev初值指向answer
如果fist和second当前指向的节点都不为null,循环遍历:
如果first.val<second.value,prev.next=first,first=first.next,prev=prev.next
否则,prev.next=second,second=second.next,prev=prev.next
循环结束之后,那么first和second只会有一个节点不为null,因为原链表已经有序,所以只需要将不为null的哪个链表添加到prev.next中即可
最终answer.next即所求
AC代码:
class Solution {public ListNode mergeTwoLists(ListNode list1, ListNode list2) {ListNode first = list1;ListNode second = list2;ListNode head = new ListNode();ListNode tem = head;while (first != null && second != null) {if (first.val < second.val) {tem.next = new ListNode(first.val);first = first.next;tem = tem.next;} else {tem.next = new ListNode(second.val);second = second.next;tem = tem.next;}}tem.next = first != null ? first : second;return head.next;}
}
递归解法
对于递归解法,首先需要定义递归函数的功能,然后定义递归的终止条件
递归函数mergeTwoLists(ListNode list1, ListNode list2):表示返回list1和list2有序合并之后的新链表的头节点
递归的终止条件:
如果其中任何一个链表为null,那么直接返回剩余的一个链表就可以了
否则:进行递归求解
如果list1.val<list2.val,这个时候list1就是合并后有序链表的头节点。也就是说递归函数返回的结果应该为list1,但是list1后面的节点和list2还没有合并,所以还不能直接返回list1,返回之前需要保证list1.next的值是list1后面的节点和list2合并之后的有序链表的头节点,这样list1才是满足结果的链表的头节点,查看递归函数的定义,经过mergeTwoLists(list.next,list2)后,list.next和list2也已经有序合并,并且递归函数的返回值就是list.next和list2有序合并后新链表的头节点,因此list1.next=mergeTwoLists(list.next,list2),然后return list1
否则,合并后有序链表的头节点为list2,list2.next的值就是list1和list2.next合并后有序链表的头节点,因此list2.next=mergeTwoLists(list, list2.next),然后return list2
AC代码
class Solution {public ListNode mergeTwoLists(ListNode list1, ListNode list2) {if (list1==null){return list2;}else if (list2==null){return list1;}else {if (list1.val< list2.val){list1.next=mergeTwoLists(list1.next,list2);return list1;}else {list2.next=mergeTwoLists(list1,list2.next);return list2;}}}
}相关文章:

21. 合并两个有序链表
题目链接:解题思路:遍历,双指针:因为两个链表有序,所以只需要依次比较两个元素的大小,然后添加到新的链表中即可first指针指向第一个链表l1,second指针指向第二个链表l2,answer保存合…...

产品经理知识体系:5.如何做好产品数据分析?
数据分析 思考 笔记 数据分析 思路 基于用户路径:用户的活动路径,操作流程等行为数据。 基于产品节点:转化率、占比 分析类型 先定性:先抛出问题、提出假设 再定量:数据验证问题、验证假设 先定性、再定量、最后得…...

详解垃圾回收算法,优缺点是什么?|金三银四系列
本文详细介绍了在 JVM 中如何判断哪些对象是需要回收的,以及不同的垃圾回收算法以及优缺点。点击上方“后端开发技术”,选择“设为星标” ,优质资源及时送达上篇文章详细介绍了 JVM 的结构以及其内存结构,需要阅读请移步。本文主要…...
 SnapshotManager 之标识文件)
Android 虚拟 A/B 详解(七) SnapshotManager 之标识文件
本文为洛奇看世界(guyongqiangx)原创,转载请注明出处。 原文链接:https://blog.csdn.net/guyongqiangx/article/details/129098176 Android 虚拟 A/B 分区《Android 虚拟 A/B 分区》系列,更新中,文章列表: Android 虚拟 A/B 详解(一) 参考资料推荐Android 虚拟 A/B 详解(二…...

LA@生成子空间@范数@衡量矩阵大小@正交化
文章目录线性组合与线性方程组生成子空间范数LpL^pLp范数向量点积用范数表示ref衡量矩阵大小特殊类型矩阵和向量对角阵向量长度性质单位向量向量单位化(正规化)正交向量正交正交向量组标准正交基正交化(schmidt)正交矩阵矩阵是正交矩阵的充要条件对称矩阵正交相似概念区分&…...

MT2012_竹鼠的白色季节
竹鼠的白色季节 #include<bits/stdc.h> #include<algorithm> using namespace std;/*思路:从小到大排序,然后依次往后遍历即可*/ int main( ) {int n,d;cin>>n>>d; int tmp;vector<int>nums;for(int i0;i<n;i){cin&…...

MySQL是什么?它有什么优势?
随着时间的推移,开源数据库在中低端应用中逐渐流行起来,占据了很大的市场份额。开源数据库具有免费使用、配置简单、稳定性好、性能优良等特点,而 MySQL 数据库正是开源数据库中的杰出代表。 开源全称为“开放源代码”。很多人认为开源软件最…...
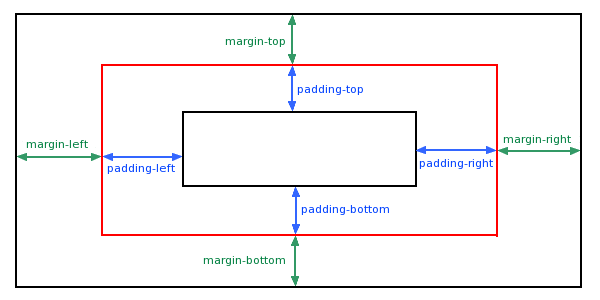
基础篇—CSS padding(填充\内边距)解析
CSS padding(填充) CSS padding(填充)是一个简写属性,定义元素边框与元素内容之间的空间,即上下左右的内边距。 属性说明padding使用简写属性设置在一个声明中的所有填充属性padding-bottom设置元素的底部填充padding-left设置元素的左部填充padding-right设置元素的右部…...

二进制枚举
一、左移:用来将一个数的各二进制位全部左移n位,低位以0补充,高位越界后舍弃。n左移1位,n<<1,相当于2*n1左移n位,1<<n,相当于2^n二、右移:将一个数的各二进制位右移N位&…...
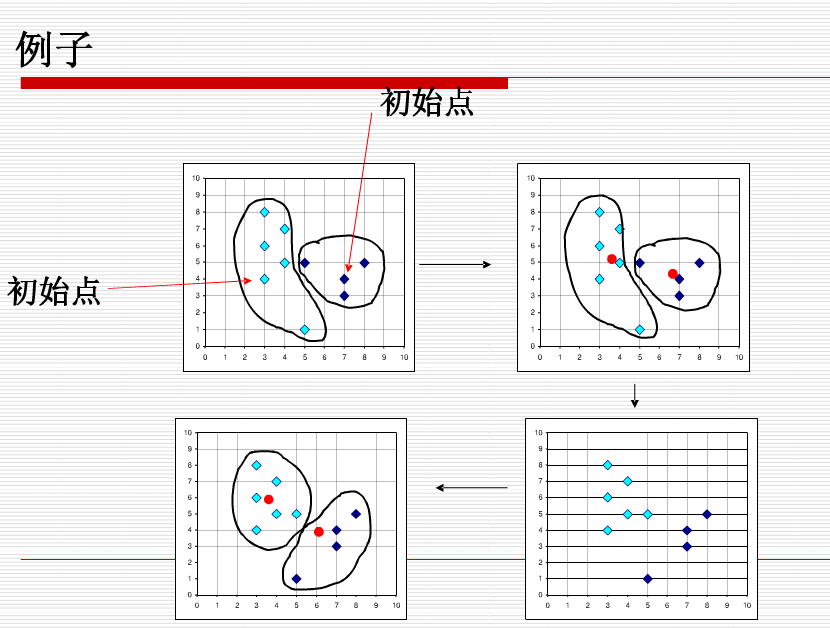
2|数据挖掘|聚类分析|k-means/k-均值算法
k-means算法k-means算法,也被称为k-平均或k-均值,是一种得到最广泛应用的聚类算法。算法首先随机选择k个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇。然后重新计…...
使用和制作动、静态库
文章目录什么是库?静态库打包方式使用方式生成并执行可执行程序粗暴方式优化方式动态库不一样的.o文件打包方式使用方式生成可执行程序运行可执行程序无法运行时的解决方案动静态库与动静态链接什么是库? 从一开始的helloworld,到现在熟练使…...

【Java基础】023 -- 集合进阶(List、Set、泛型、树)
目录 一、集合的体系结构 1、单列集合(Collection) 二、Collection集合 1、Collection常见方法 ①、代码实现: ②、contains方法重写equals方法示例:(idea可自动重写) 2、Collection的遍历方式(…...
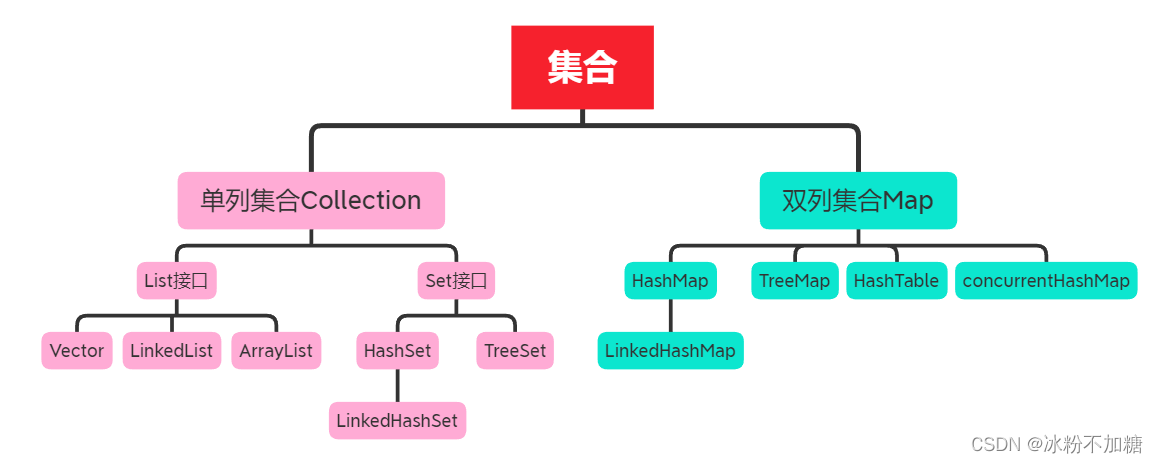
面试题整理01-集合详解
文章目录前言一、集合的整体结构单列集合接口:双列集合接口:二、单列集合详解1.List接口1.1 ArrayList集合特点:扩容:添加元素遍历1.2 LinkedList集合特点:添加元素:2.Set接口2.1 HashSet集合特点ÿ…...
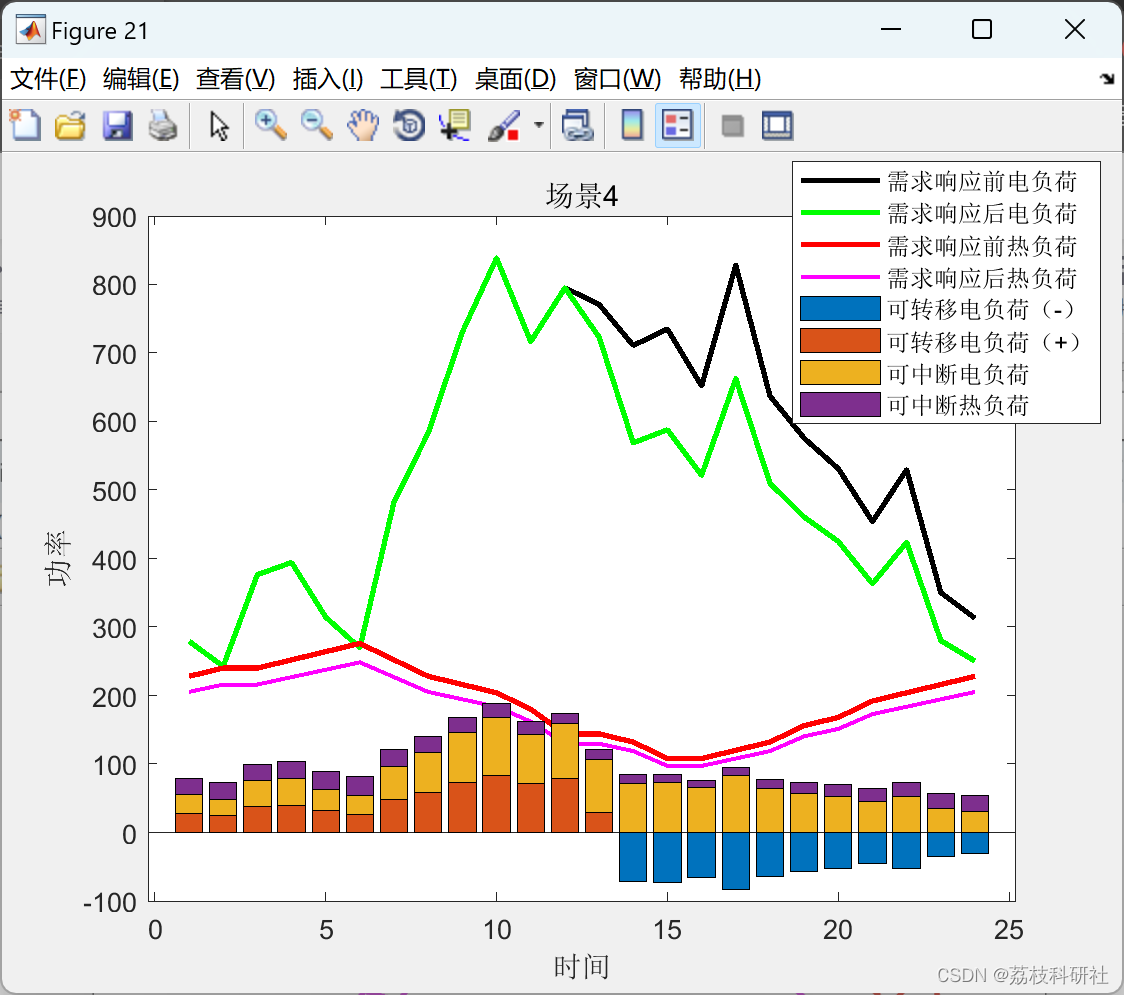
数据驱动的两阶段分布鲁棒(1-范数和∞-范数约束)的电热综合能源系统研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

ArcGIS网络分析之发布网络分析服务(二)
在上一篇中讲述了如何构建网络分析数据集,本篇将讲解如何发布网络分析服务。本文将使用上一篇中建立的网络数据集,下载地址在上一篇博文的最后已给出。 之前我们已经实现了基于ArcMap中的网络分析,但是仅仅支持本地是万万不够的,这里我们的目的就是将我们建好的网络分析图…...

js实现元素样式切换的基本功能
需求:用户第一次点击某些元素,改变元素的某些样式,比如背景颜色,字体颜色。用户第二次点击某些元素,恢复之前的样式。.....思路:准备一定量的div盒子,并取相同的类名<div class"box&quo…...

java 策略模式 + 工厂模式 实例
一 前言 经常听说各种设计模式,知道理论,也知道应该使用,但具体怎么用,什么时候用,使用的优点一直比较模糊,今天写一个项目中经常用到的模式,来具体理解。项目中经常用到工厂模式或者策略模式&…...
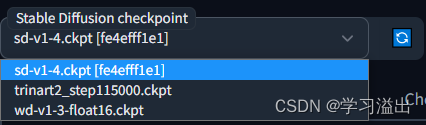
本地生成动漫风格 AI 绘画 图像|Stable Diffusion WebUI 的安装和部署教程
Stable Diffusion WebUI 的安装和部署教程1. 简介2. Windows安装环境3. 运行4. 模型下载链接5. 其他资源1. 简介 先放一张WebUI的图片生成效果图,以给大家学习的动力 :) 怎么样,有没有小小的心动?这里再补充一下&…...

华为OD机试 - 异常的打卡记录 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
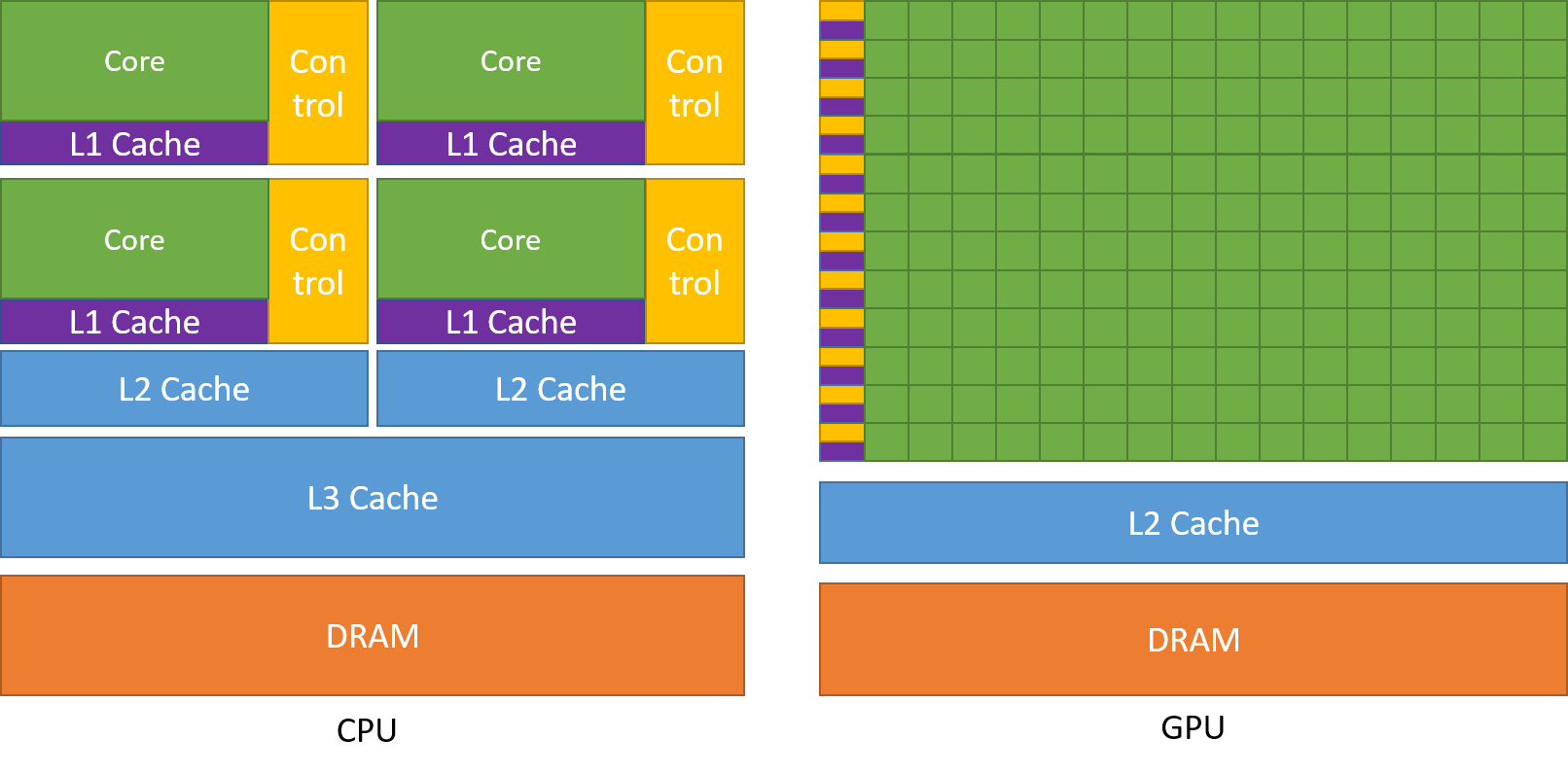
「机器学习笔记」之深度学习基础概念(基于Pytorch)
本文以 Pytorch 为线索,介绍人工智能和深度学习相关的一些术语、概念。 关于发展历史您也可以阅读深度学习神经网络之父 Jrgen Schmidhuber 所写的《Annotated History of Modern AI and Deep Learning(现代人工智能和深度学习的注释版历史)…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
