Sequence 2023牛客暑期多校训练营6 E
登录—专业IT笔试面试备考平台_牛客网
题目大意:有一长度为n的数组a,有q次询问,每次要求将[l,r]的区间分成k个连续区间,满足每个区间和都是偶数,能满足要求就输出YES
1<=n,q<=1e5;0<=ai<=1e10;1<=l<=r<n;1<=k<=1e5
思路:要想和为偶数,那么奇数的数量必须是偶数个,所以我们把数组中的数都变成%2后的结果,也就是整个数组只有0和1构成,每个0可以作为一个合法的区间,而每个1必须要和其相邻的一个1组合才能构成一个最小的合法区间,而如果一个1和其相邻的一个1组成一个区间,那这两个1中间的0都不能作为合法的区间。
所以我们要分两种情况讨论,一种是数组中从左往右第二个1和第一个1组合,另一种是第二个和第三个1组合,然后分别对合法区间数求前缀和,每个0的贡献都是1,每个含有两个1的区间,整个区间贡献是1,例如对于0 0 1 0 0 1 0 0 1 0 0 1 0这个数组,第一个前缀和数组sum1求出来的是1 2 3 3 3 3 4 5 6 6 6 6 7,第二个数组sum2是0 0 0 1 2 3 3 3 3 4 5 6 6,另外,还要特判一下每个区间内1的数量是否是偶数,如果是奇数就可以直接输出no了。
对于其他情况,我们要看每个询问的区间适用于哪个数组,如果a[r]是1,那么哪个数组的sum[r]=sum[r-1],说明哪个数组是合法的,如果a[r]是0,那么就看哪个sum[r]!=sum[r-1],不等的那个数组提供贡献
#include<bits/stdc++.h>
//#include<__msvc_all_public_headers.hpp>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
const ll MOD = 998244353;
ll a[N];
ll sum[N];
ll sum2[N];
ll sum3[N];
void solve()
{int n, q;cin >> n >> q;for (int i = 1; i <= n; i++){cin >> a[i];a[i] %= 2;//将数组按奇偶转换成1和0sum[i] = sum[i - 1] + a[i];//统计区间奇偶性sum2[i] = sum3[i] = 0;}int flag = 0;for (int i = 1; i <= n; i++){if (!a[i]){if(!flag)sum2[i] = 1;//在两个1中间以外的0贡献为1}else{if (!flag){flag = i;//记录上一个1的位置}else{sum2[flag]++;//上一个1到这一个1之间总共贡献1flag = 0;}} }if (flag)//末尾没有匹配的1要+1贡献与前面的0区分开sum2[flag]++;flag = 0;int fi=0;for (int i = 1; i <= n; i++){if (!a[i]){if(!fi)//在遇到第一个1之前不记录贡献continue;if (!flag)sum3[i] = 1;}else{if(!fi){fi=i;//遇到第一个1之后,后面的统计与上一个数组相同continue;}if (!flag){flag = i;}else{sum3[flag]++;flag = 0;}}}if (flag)sum3[flag]++;for (int i = 2; i <= n; i++){//求前缀和得到区间内的合法区间数sum2[i] = sum2[i - 1] + sum2[i];sum3[i] = sum3[i - 1] + sum3[i];}for (int i = 1; i <= q; i++){int l, r, k;cin >> l >> r >> k;if ((sum[r] - sum[l - 1]) % 2!=0){cout << "NO" << endl;continue;}ll ans3 = sum3[r] - sum3[l - 1];ll ans2 = sum2[r] - sum2[l - 1];if (a[r] == 1){//右端点是1,哪个数组r=r-1就说明哪个合法if (sum2[r] == sum2[r - 1]){cout << (ans2 >= k ? "YES" : "NO") << endl;}else{cout << (ans3 >= k ? "YES" : "NO") << endl;}}else{//右端点是0,哪个数组r!=r-1就说明哪个合法if (sum2[r] != sum2[r - 1]){cout << (ans2 >= k ? "YES" : "NO") << endl;}else{cout << (ans3 >= k ? "YES" : "NO") << endl;}}}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin >> t;while (t--){solve();}return 0;
}相关文章:

Sequence 2023牛客暑期多校训练营6 E
登录—专业IT笔试面试备考平台_牛客网 题目大意:有一长度为n的数组a,有q次询问,每次要求将[l,r]的区间分成k个连续区间,满足每个区间和都是偶数,能满足要求就输出YES 1<n,q<1e5;0<ai<1e10;1<l<r&l…...

【ASP.NET MVC】使用动软(二)(10)
一、添加动软生成工程 按前文添加动态到工程 双击动软 完成新建数据库服务器后 ,需要关闭重新打开 选择简单三层,注意保存位置 注意切换数据库: 生成后拷贝五个文件夹到工程目录 注意目录结构: 添加四个项目到原来的工程&…...

STM32入门学习之独立看门狗(IWDG)
1.STM32的独立看门狗是一个具有独立时钟的片上外设。通常,为了防止程序卡死,可以设置看门狗定时复位。当看看门狗被使能之后,会按初始化时设置的计数值进行计数。当根据计数值计数的倒数时间为0时,便会自动复位程序,即…...

抖音seo矩阵系统源码搭建开发详解
抖音SEO矩阵系统是一个用于提高抖音视频在搜索引擎排名的工具。如果你想开发自己的抖音SEO矩阵系统,以下是详细的步骤: 开发步骤详解: 确定你需要的功能和算法 抖音SEO矩阵系统包含很多功能,比如关键词研究、内容优化、链接建设、…...
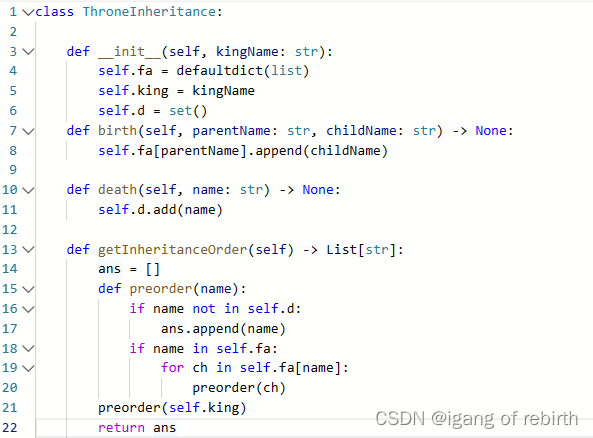
2685. 统计完全连通分量的数量;2718. 查询后矩阵的和;1600. 王位继承顺序
2685. 统计完全连通分量的数量 核心思想:枚举所有的连通分量,然后判断这些连通分量是不是完全连通分量,完全连通分量满足边数2e 点数v(v-1)。 2718. 查询后矩阵的和 核心思想:后面的改变更重要,所以我们直接逆向思维…...

SpringBoot统一功能处理(AOP思想实现)(统一用户登录权限验证 / 异常处理 / 数据格式返回)
主要是三个处理: 1、统一用户登录权限验证; 2、统一异常处理; 3、统一数据格式返回。 目录 一、用户登录权限校验 🍅 1、使用拦截器 🎈 1.1自定义拦截器 🎈 1.2 设置自定义拦截器 🎈创建cont…...

git stash 用法
起始 今天在看一个bug,之前一个分支的版本是正常的,在新的分支上上加了很多日志没找到原因,希望回溯到之前的版本,确定下从哪个提交引入的问题,但是还不想把现在的修改提交,也不希望在Git上看到当前修改的…...

生鲜蔬果小程序的完整教程
随着互联网的发展,线上商城成为了人们购物的重要渠道。其中,小程序商城在近年来的发展中,备受关注和青睐。本文将介绍如何使用乔拓云网后台搭建生鲜果蔬配送小程序,并快速上线。 首先,登录乔拓云网后台,进入…...

De Bruijin序列与魔术(二)——魔术《De Bruijin序列》
早点关注我,精彩不错过! 上一篇我们介绍了De Bruijin序列的基本数学内容以及其如何应用在魔术上的一些基本内容,今天我们就来学习一下这个经典的《De Bruijin序列》魔术。 De bruijin序列魔术 先看视频。 视频1 De Bruijin序列的魔术 魔术来源…...
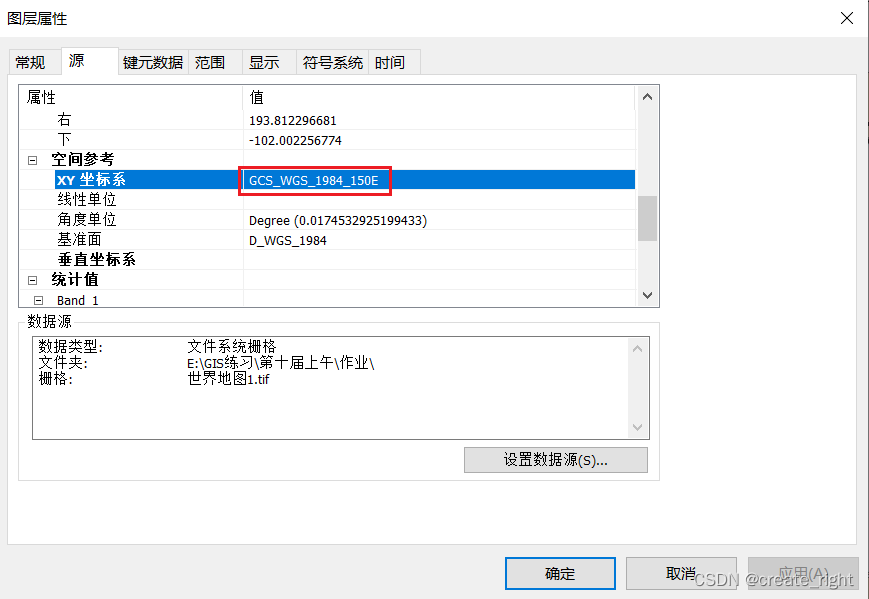
ARCGIS地理配准出现的问题
第一种。已有省级行政区矢量数据,在网上随便找一个相同省级行政区图片,利用地理配准工具给图片添加坐标信息。 依次添加省级行政区选择矢量数据、浙江省图片。 此时,图层默认的坐标系与第一个加载进来的省级行政区选择矢量数据的坐标系一致…...
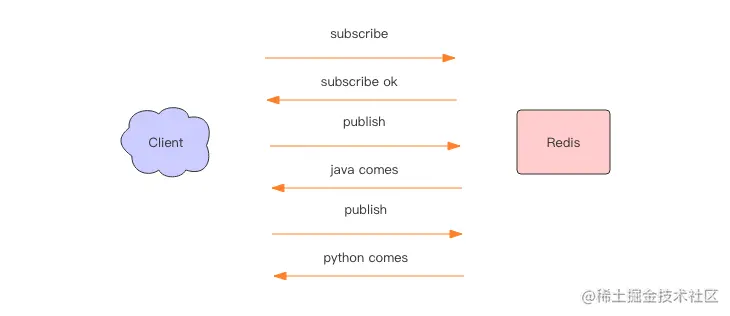
redis原理 6:小道消息 —— PubSub
前面我们讲了 Redis 消息队列的使用方法,但是没有提到 Redis 消息队列的不足之处,那就是它不支持消息的多播机制。 img 消息多播 消息多播允许生产者生产一次消息,中间件负责将消息复制到多个消息队列,每个消息队列由相应的消费组…...
Android Studio 的Gradle版本修改
使用Android Studio构建项目时,需要配置Gradle,与Gradle插件。 Gradle是一个构建工具,用于管理和自动化Android项目的构建过程。它使用Groovy或Kotlin作为脚本语言,并提供了强大的配置能力来定义项目的依赖关系、编译选项、打包方…...

Redis的部分面试题
1.Redis是什么?简述它的优缺点? Redis的字符串类型是通过简单动态字符串SDS来实现的。简单动态字符串是Redis自己实现的一种字符串表示方式,相比于C语言中的传统字符串,它具有以下几个特点: 1. 动态调整大小:简单动态字符串可…...

单通道 6GSPS 16位采样DAC子卡模块--【资料下载】
FMC147是一款单通道6.4GSPS(或者配置成2通道3.2GSPS)采样率的12位AD采集、单通道6GSPS(或配置成2通道3GSPS)采样率16位DA输出子卡模块,该板卡为FMC标准,符合VITA57.4规范,该模块可以作为一个理想…...

Python 文件操作详解
概要 Python进行文件操作,在日常编程中是很常用的。为了方便大家,这里对各种文件操作的知识进行汇总。一文在手,无须它求!来一起学习吧。 一、文件的打开和关闭 open()函数 f1 open(rd:\测试文件.txt, moder, encodingutf-8) c…...

【Rust 基础篇】Rust Never类型:表示不会返回的类型
导言 Rust是一种以安全性和高效性著称的系统级编程语言,其设计哲学是在不损失性能的前提下,保障代码的内存安全和线程安全。在Rust中,Never类型是一种特殊的类型,它表示一个函数永远不会返回。Never类型在Rust中有着重要的应用场…...

error “Component name “*****“ should always be multi-word”解决方案
问题 在 vue-cli 创建的项目中,创建文件并命名后,会报 “Component name "*****" should always be multi-word” 报错; Component name "index" should always be multi-word.eslintvue/multi-word-component-names原…...

前后端开发的区别是什么?
VUE的开发方式为什么和后端的MVC开发方式不一样呢? 实际上,Vue 和后端开发的 MVC(Model-View-Controller)方式是不同的,因为它们面对的问题和场景也不同。 前端与后端的职责不同: 前端和后端的职责和任务不…...
小白电脑装机(自用)
几个月前买了配件想自己装电脑,结果最后无法成功点亮,出现的问题是主板上的DebugLED黄灯常亮,即DRAM灯亮。对于微星主板的Debug灯,其含义这篇博文中有说明。 根据另一篇博文,有两种可能。 我这边曾将内存条和主板一块…...

Quic协议 0-RTT
目录 1、Quic协议 2、Quic直接通过TLS握手进行建立链接,TLS是1.3版本 3.1、通过缓存服务器公钥实现0-RTT,服务器 通过kdf密钥派生机制,来产生会话加密key,保证数据向前安全性 3.2、通过PKN来实现数据重传保证数据完整性&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
