强化学习基础知识

强化学习是一种机器学习方法,通过agent与environment的互动,学习适当的action policy以取得更大的奖励reward。本篇博客介绍强化学习的基础知识,与两类强化学习模型。
目录
- 强化学习的基础设定
- policy based 强化学习的目标
- 3个注意事项
- 实际训练过程
- 重要性采样
- value based 强化学习的目标
- Temporal Differential learning (TD learning)
- 参考
强化学习的基础设定
强化学习和监督学习,非监督学习一样是一种基本学习模式,在强化学习的框架中,一共有2个主体:agent与environment。environment会给agent一些状态信息state,agent可以根据state的情况进行action的选择,并从environment获得一些奖励reward。

强化学习分为2类:policy based和value based。二者并非互斥关系,存在一些模型既是policy based又是value based 例如:A3C[ICML2016]。
policy based 强化学习的目标
强化学习的目标是学习一个policy使得最终全场决策下来得到的总reward最大。具体展开而言,给定一个state,agent决策采取action的策略模型,用π\piπ表示,π\piπ的参数是θ\thetaθ,由于policy根据state采取action,我们可以用公式:a=πθ(s)a=\pi_\theta(s)a=πθ(s)表示。当agent做出action操作后,environment会给出一个reward并更新状态,至此一轮决策结束。多轮决策组成一个由state, action, reward组成的序列,我们定义为τ=(s1,a1,r1,...sT,aT,rT)\tau=(s_1, a_1,r_1,...s_T,a_T,r_T)τ=(s1,a1,r1,...sT,aT,rT)。RτR_\tauRτ是整场决策结束后总共的奖励,Rτ=∑t=1TrtR_\tau=\sum_{t=1}^Tr_tRτ=∑t=1Trt,强化学习的目的是最大化RτR_\tauRτ。
在实际决策过程中,即便π\piπ和environment不变,每一步的action依旧有随机性,因而最终的奖励RτR_\tauRτ也不会完全一致,而是具有一些随机性。因此强化学习的目标为最大化一个π\piπ下的平均RτR_\tauRτ,即E[Rτ]=∑τR(τ)p(τ∣θ)E[R_\tau]=\sum_{\tau}R(\tau)p(\tau|\theta)E[Rτ]=∑τR(τ)p(τ∣θ),很显然我们无法得到准确的期望,因为我们无法把一个参数设定下所有的决策路径全都取一个遍,因而实际使用中,通过采样取平均值的方法得到一个期望的近似值。R(θ)≈1N∑n=1NR(τn)R(\theta)\approx \frac{1}{N}\sum_{n=1}^{N}R(\tau_n)R(θ)≈N1∑n=1NR(τn)。
强化学习的优化目标即为:R(θ)≈1N∑n=1NR(τn)R(\theta)\approx \frac{1}{N}\sum_{n=1}^{N}R(\tau_n)R(θ)≈N1∑n=1NR(τn)。
通过梯度下降提升优化目标,这一步需要求R(θ)R(\theta)R(θ)的导数。∇Rθ=∑τR(τ)∇p(τ∣θ)=∑τR(τ)p(τ∣θ)∇p(τ∣θ)p(τ∣θ)=∑τR(τ)p(τ∣θ)∇log(p(τ∣θ))p(τ∣θ)=p(s1)p(a1∣s1)p(s2,r1∣s1,a1)...p(sT,rT−1∣sT−1,aT)log(p(τ∣θ))=log(p(s1))+∑t=1Tlog(p(at∣st,θ))+∑t=1Tlog(p(rt,st−1∣st,at))∇log(p(τ∣θ))=∑t=1T∇log(p(at∣st,θ))\nabla R_\theta=\sum_{\tau}R(\tau)\nabla p(\tau|\theta)=\sum_{\tau} R(\tau)p(\tau|\theta)\frac{\nabla p(\tau|\theta)}{p(\tau|\theta)}=\sum_{\tau}R(\tau)p(\tau|\theta)\nabla log(p(\tau|\theta))\\ p(\tau|\theta)=p(s_1)p(a_1|s_1)p(s_2,r_1|s_1,a_1)...p(s_T,r_{T-1}|s_{T-1},a_{T})\\ log(p(\tau|\theta))=log(p(s_1))+\sum_{t=1}^Tlog(p(a_t|s_t,\theta))+\sum_{t=1}^Tlog(p(r_t,s_{t-1}|s_t,a_t))\\ \nabla log(p(\tau|\theta))=\sum_{t=1}^T\nabla log(p(a_t|s_{t},\theta))∇Rθ=τ∑R(τ)∇p(τ∣θ)=τ∑R(τ)p(τ∣θ)p(τ∣θ)∇p(τ∣θ)=τ∑R(τ)p(τ∣θ)∇log(p(τ∣θ))p(τ∣θ)=p(s1)p(a1∣s1)p(s2,r1∣s1,a1)...p(sT,rT−1∣sT−1,aT)log(p(τ∣θ))=log(p(s1))+t=1∑Tlog(p(at∣st,θ))+t=1∑Tlog(p(rt,st−1∣st,at))∇log(p(τ∣θ))=t=1∑T∇log(p(at∣st,θ))
最终得到∇Rθ\nabla R_\theta∇Rθ的表达式:∇Rθ≈1N∑n=1N∑t=1TR(τn)∇log(p(at∣st,θ))\nabla R_\theta \approx \frac{1}{N}\sum_{n=1}^N\sum_{t=1}^TR(\tau_n) \nabla log(p(a_t|s_{t},\theta))∇Rθ≈N1∑n=1N∑t=1TR(τn)∇log(p(at∣st,θ)) (*)
3个注意事项
- 为什么要构成log的形式:进行归一化,降低采样偶然性对于低
reward但高频对梯度的影响 - 由于采样具有偶然性,考虑到不被采样到的点以及R(τ)R(\tau)R(τ)有时候可能一直取正数,将公式里的R(τ)R(\tau)R(τ)替换为R(τ)−bR(\tau)-bR(τ)−b进行修正
- (*)给每个梯度的权重只考虑了整场决策的
reward,忽略了每个action的独特性,对其进行改进,我们引入advantage function:Aθ(st,at)A^\theta(s_t,a_t)Aθ(st,at)用于衡量sts_tst状态下采用ata_tat相对于其他action有多好的程度。
实际训练过程
给定初始化的参数θ0\theta_0θ0,采样NNN个τ\tauτ计算每个τ\tauτ的reward,计算当前参数下的∇log(p(at∣st,θ))\nabla log(p(a_t|s_{t},\theta))∇log(p(at∣st,θ)),进行参数θ\thetaθ的梯度更新得到θ1\theta_1θ1,然后对新得到的参数进行下一轮的采样与梯度更新直至训练停止。
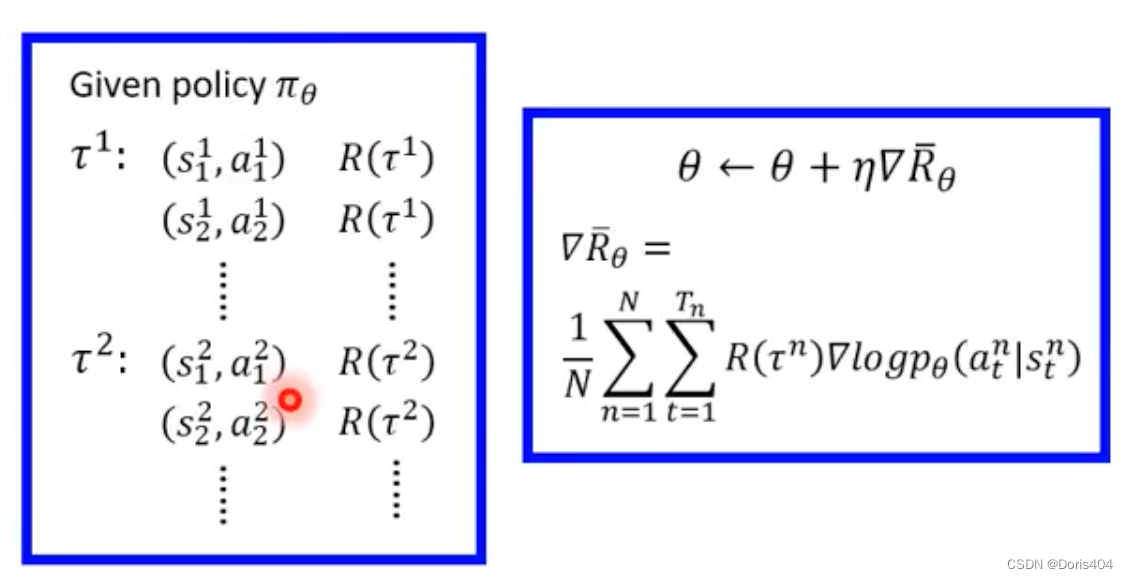
这种训练方法被有一个问题:每次更新参数都需要重新采样,消耗了大量的时间。因而提出了off policy的方法减少采样带来的时间开销。
重要性采样
重要性采样(importance sampling)方法可以减小采样的个数,极大地提升了采样的效率。其具体实现如下:假定我们有一个分布ppp,我们从分布ppp中进行采样得到xxx,我们希望计算得到函数f(x)f(x)f(x)的期望值,即Ex∼p[f(x)]E_{x\sim p}[f(x)]Ex∼p[f(x)]。一个直观的思路是我们先根据分布ppp采样NNN个点,然后计算这NNN个点的均值作为期望的估计。然而有时候我们无法直接从分布ppp进行采样,这种时候可以从一个与分布ppp接近的分布qqq进行采样,然后将结果转化为依据分布ppp采样的均值。
Ex∼p[f(x)]=Ex∼q[f(x)p(x)q(x)]E_{x\sim p}[f(x)]=E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]Ex∼p[f(x)]=Ex∼q[f(x)q(x)p(x)]这里的分布qqq应该尽可能接近分布ppp时,公式才能在采样意义下成立。
off policy的方法使用重要性采样的方法降低了采样的次数进而减小了采样带来的时间开销。on policy方法与off policy方法最大的区别就是二者采样的方式是不同的,on policy方法使用梯度下降方法更新参数后按照新参数进行采样,而off policy方法依旧使用之前旧参数采样的结果(这里假设了参数更新并未很多因而分布变化并不大)。
on policy:∇Rθ=Eτ∼pθ(τ)[R(τn)∇log(pθ(τ))]\nabla R_\theta=E_{\tau \sim p_\theta(\tau)}[R(\tau_n)\nabla log(p_\theta(\tau))]∇Rθ=Eτ∼pθ(τ)[R(τn)∇log(pθ(τ))]
off policy:∇Rθ=Eτ∼pθ′(τ)[R(τn)pθ(τ)pθ′(τ)∇log(pθ(τ))]\nabla R_\theta=E_{\tau \sim p_{\theta '}(\tau)}[R(\tau_n)\frac{p_\theta(\tau)}{p_{\theta '}(\tau)}\nabla log(p_\theta(\tau))]∇Rθ=Eτ∼pθ′(τ)[R(τn)pθ′(τ)pθ(τ)∇log(pθ(τ))]
可以发现off policy在参数设定为θ′\theta 'θ′下进行采样,梯度下降更新的是θ\thetaθ而非θ′\theta 'θ′,因此采样可以复用。
value based 强化学习的目标
与policy based强化学习不同,value based模型通过神经网络学习environment针对给定state以及action的reward,帮助agent进行当前state进行action的决策。value based强化学习假定存在一个类似于先知的函数Q(s,a;θ)Q(s,a;\theta)Q(s,a;θ)它可以在给定state的条件下计算出每个action的奖励期望是多大,并且用一个神经网络来学习它。有了这样的先知后,模型自然可以通过选择当前state下reward最高的action进行操作。
Temporal Differential learning (TD learning)
TD learning是训练上述Q(s,a;θ)Q(s,a;\theta)Q(s,a;θ)模型的方法,其训练思想基于监督学习,需要一个“真实标签”。但由于真实标签在这个训练场景下获取需要大量时间开销,因此我们会用TD target来拟合真实的标签即拟合真实的rewardyt=rt+maxγQ(st+1,at+1;θ)y_t=r_t+\max \gamma Q(s_{t+1}, a_{t+1}; \theta)yt=rt+maxγQ(st+1,at+1;θ),并使用梯度下降方法来使得Q(st,at;θ)Q(s_t,a_t;\theta)Q(st,at;θ)接近yty_tyt。
参考
- 价值学习__Value-Based_Reinforcement_Learning(ps:这个up也出了视频介绍policy-based reinforcement learning视频不长,讲的很清晰)
- 李弘毅老师强化学习教学视频合集(ps:里面有一些视频内容是重合的可以挑着看)
相关文章:

强化学习基础知识
强化学习是一种机器学习方法,通过agent与environment的互动,学习适当的action policy以取得更大的奖励reward。本篇博客介绍强化学习的基础知识,与两类强化学习模型。 目录强化学习的基础设定policy based 强化学习的目标3个注意事项实际训练…...
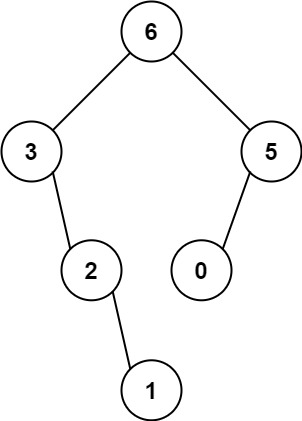
LeetCode230218_148、654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums 构建的 最大二叉树…...

WordPress 是什么?.com 和 .org 的 WordPress 有什么差异?
本篇文章会介绍这次WordPress 5.8核心版本所带来的其中一项新功能:内存块小工具(Widget)此次更新把小工具编辑设定的页面也改成用「内存块编辑」的概念,就跟内置的「古腾堡」编辑器一样,把所有元件都内存块化ÿ…...

java8新特性【2023】
Lambda表达式 新的一套语法规则 是一个匿名函数 Testpublic void test1(){Runnable r1 new Runnable(){Overridepublic void run() {System.out.println("线程A");}};r1.run();System.out.println("");Runnable r2 () -> System.out.println("…...

刷题记录:牛客NC51101Lost Cows
传送门:牛客 题目描述: (2≤N≤8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment, they visited the neighborhood watering hole and drank a few too many beers before dinner. When it was time to line up for their ev…...

华为OD机试 - 不等式 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 最小叶子节点 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 最近的点 | 备考思路,刷题要点,答疑 【新解法】华…...

GuLi商城-SpringCloud-OpenFeign测试远程调用
1. Feign 简介 Feign 是一个声明式的 HTTP 客户端,它的目的就是让远程调用更加简单。Feign 提供了HTTP请 求的模板,通过编写简单的接口和插入注解,就可以定义好 HTTP 请求的参数、格式、地址等信 息。Feign 整合了 Ribbon(负载…...
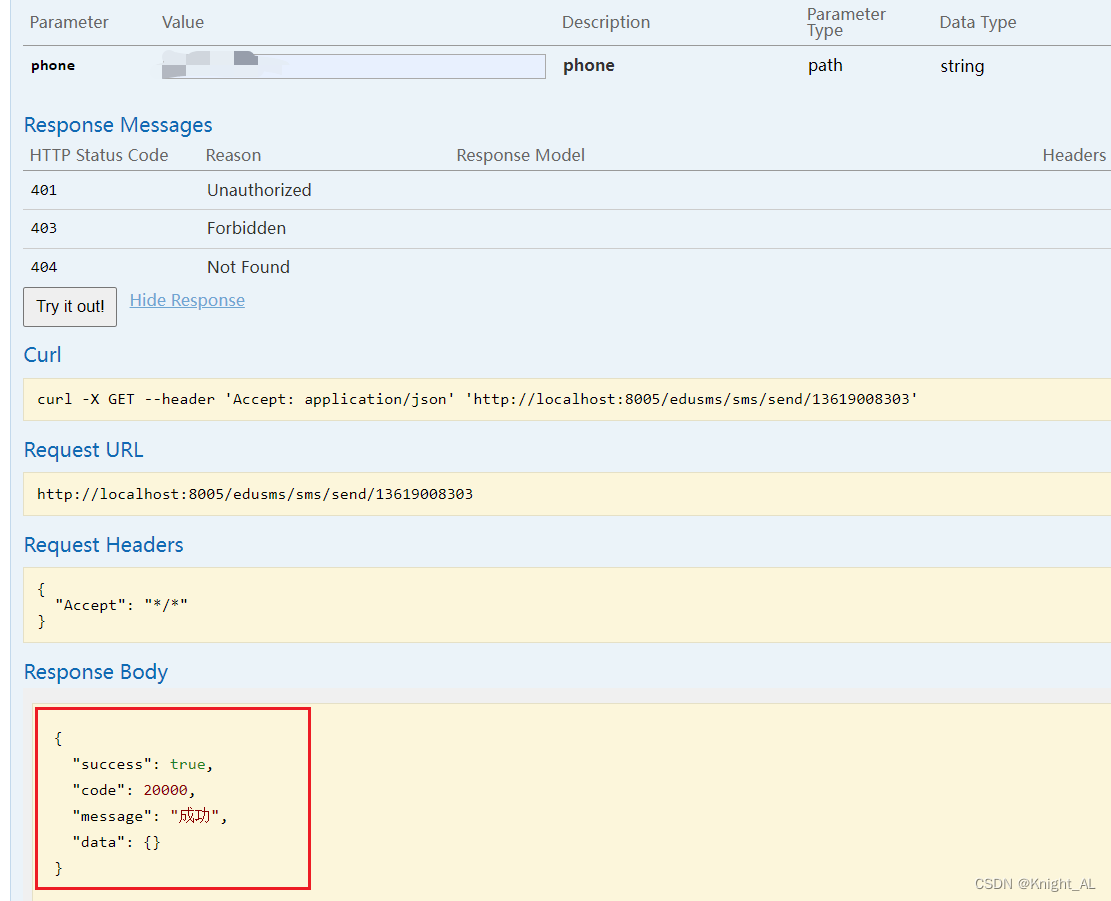
阿里云_山东鼎信短信的使用(云市场)
目录山东鼎信API工具类随机验证码工具类进行测试Pom依赖(可以先导入依赖)创建controllerSmsServiceSmsServiceImplswagger测试(也可以使用postman)山东鼎信API工具类 山东鼎信短信官网 找到java的Api,复制下来 适当改了一下,为了调用(类名SmsUtils) p…...

基于虚拟机机的代码保护技术
虚拟机保护技术是基于x86汇编系统的可执行代码转换为字节码指令系统的代码,以达到保护原有指令不被轻易逆向和篡改的目的。 字节码(Byte-code)是一种包含执行程序,由一序列 op 代码/数据对组成的 ,是一种中间码。字节是…...
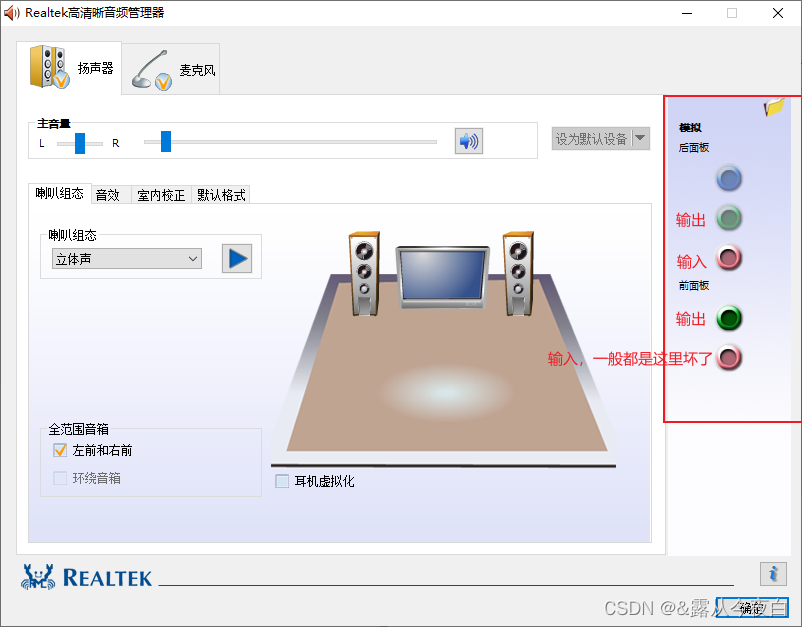
Win10耳机有声音麦不能说话怎么办?麦克风说话别人听不到解决方法
网上找了一些解决办法,一般都是重复的,几个设置调来调去也就那样,没什么用 这种问题一般是“老式”一点的台式机会出现,提供的解决办法如下: 首先下载带面板的音频管理器,如realtek高清晰音频管理器&…...
 Final Round 题解)
The 22nd Japanese Olympiad in Informatics (JOI 2022/2023) Final Round 题解
交题:https://cms.ioi-jp.org/documentation A 给一个序列 a1,⋯,ana_1,\cdots,a_na1,⋯,an。 执行nnn个操作,第iii个操作为找出第iii个数前离其最近且与它相同的数的位置,把这两个数之间的数全部赋值aia_iai。求最后的序列。 考虑第…...

openEuler RISC-V 成功适配 VisionFive 2 单板计算机
近日,RISC-V SIG 成功在 VisionFive 2 开发板上适配欧拉操作系统,目前最新版本的 openEuler RISC-V 22.03 V2 镜像已在 VisionFive 2 开发板上可用,这是 openEuler 推动 RISC-V 生态演进的又一新进展。下载链接https://mirror.iscas.ac.c…...
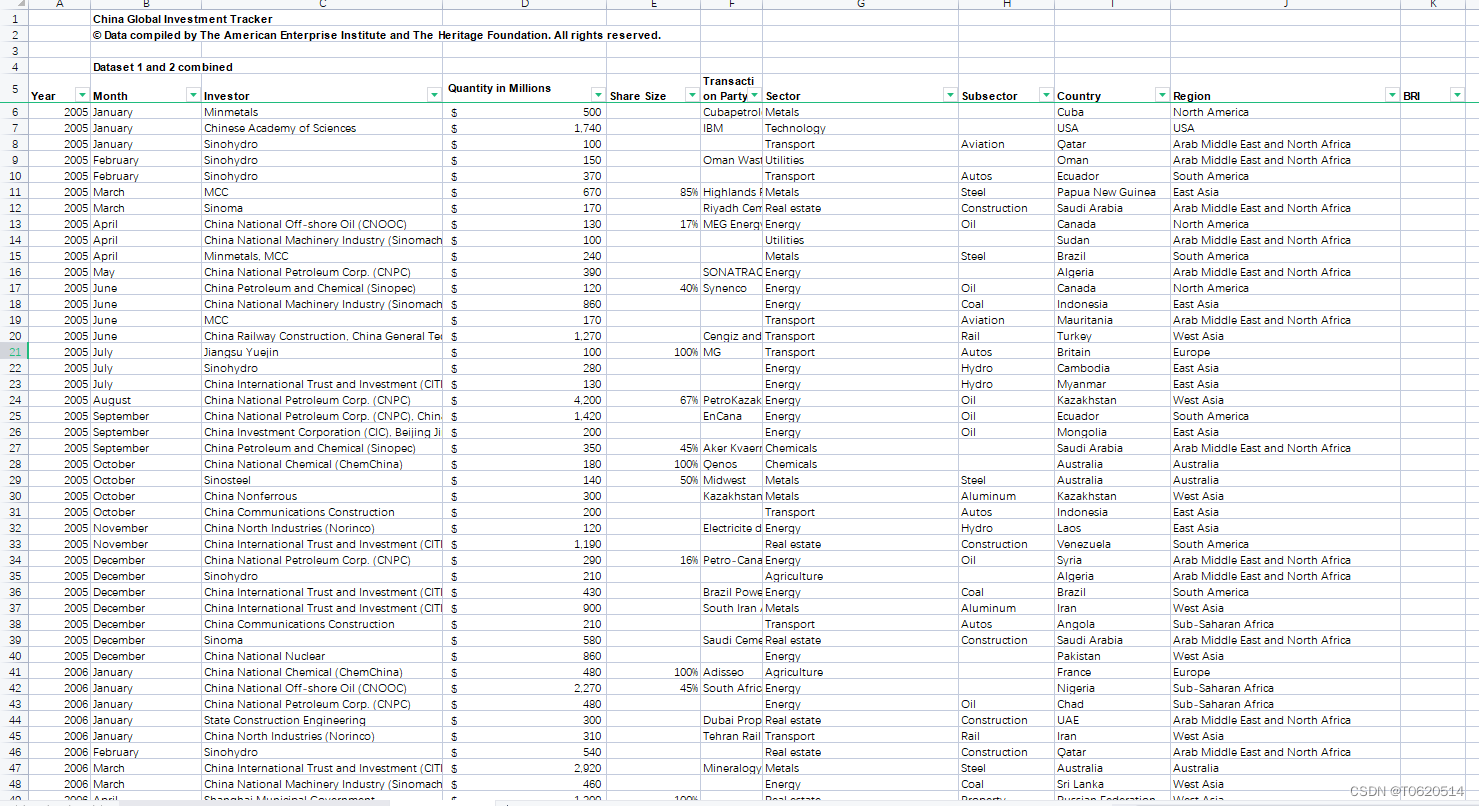
2005-2022中国企业对外直接投资、OFDI海外投资明细、中国全球投资追踪数据CGIT(含非建筑施工类问题投资)
中国全球投资跟踪”(China Global Investment Tracker),数据库,美国企业研究所于1月28日发布。数据库显示,2005年以来,中国对外投资和建设总额已接近2万亿美元。该数据库是唯一一套涵盖中国全球投资和建设的…...
PCB学习笔记——使用嘉立创在线绘制原理图与PCB
嘉立创软件地址:https://lceda.cn/ 新建工程-新建原理图,在元件库中可以搜索元器件,可以直接放置在原理图上。 原理图绘制完成后,保存文件,设计-原理图转PCB,可以直接生成对应的PCB,设置边框&…...

【C++】类型转化
🌈欢迎来到C专栏~~类型转化 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&…...

Mybatis -- resultMap以及分页
查询为null问题 要解决的问题:属性名和字段名不一致 环境:新建一个项目,将之前的项目拷贝过来 1、查看数据库的字段名 2、Java中的实体类设计 public class User { private int id; //id private String name; //姓名 private String passwo…...
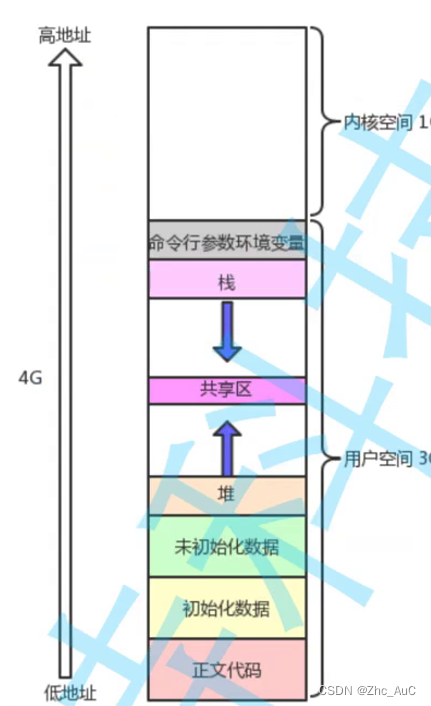
Linux之进程
一.冯诺依曼体系 在计算机中,CPU(中央处理器)是不直接跟外部设备直接进行通信的,因为CPU处理速度太快了,而设备的数据读取和输入有太慢,而是CPU以及外设直接跟存储器(内存)打交道&am…...

结构体——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是结构体噢,之前我们在初始C语言中其实就已经学习过了结构体的知识,但是不是很全面,这次,我们也只是稍微详细一点,敬请期待小雅兰之后的博客ÿ…...

CCNP350-401学习笔记(51-100题)
51、Which statement about a fabric access point is true?A. It is in local mode and must be connected directly to the fabric edge switch. B. It is in local mode and must be connected directly to the fabric border node C. It is in FlexConnect mode and must …...
C语言学习_DAY_4_判断语句if_else和分支语句switch_case【C语言学习笔记】
高质量博主,点个关注不迷路🌸🌸🌸! 目录 1.案例引入 2.if判断语句的语法与注意事项 3.switch多分支语句的语法与注意事项 前言: 书接上回,我们已经学习了所有的数据类型、运算符,并且可以书写…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
