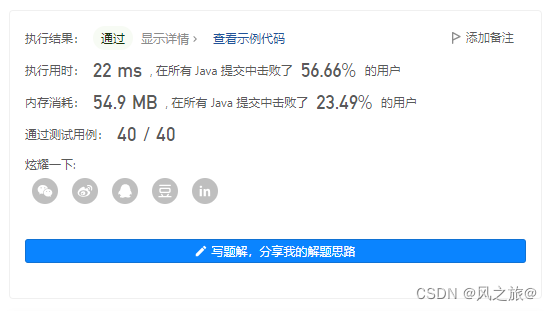
215. 数组中的第K个最大元素(快排+大根堆+小根堆)
题目链接:力扣
解题思路:
方法一:基于快速排序
因为题目中只需要找到第k大的元素,而快速排序中,每一趟排序都可以确定一个最终元素的位置。
当使用快速排序对数组进行降序排序时,那么如果有一趟排序过程中,确定元素的最终位置为k-1(索引从0开始),那么,该元素就是第k大的元素。
具体思想下:
- 利用快排,对数组num[left,...,right]进行降序排序,在一趟排序过程中,可以确定一个元素的最终位置p,将数组划分为三部分,num[left,...,p-1],nums[p],nums[p+1,right],并且满足
- num[left,...,p-1] >= nums[p]
- num[p+1,right] <=nums[p]
- 即p位置以前的元素是数组中比p位置元素大的元素(此时p位置以前的元素不一定有序,但是肯定都大于等于p位置的元素),而num[p]是第p+1大的元素
- 因为需要找到的是第k大的元素:
- 如果k < p,那么第k大的元素肯定在num[left,...,p-1]内,这个时候只需要对右半部分区间进行快排
- 如果k > p,那么第k大的元素肯定在nums[p+1,right]区间内,这个时候只需要对左半部分区间进行快排
- 如果 p= k-1,那么nums[p]就是第k大的元素
- 注意这种方式并不要求最终数组中的元素有序,每次只会对左半部分或者右半部分进行快排,减少了一半的快排调用
AC代码:
class Solution {public static int findKthLargest(int[] nums, int k) {return quickSortFindK(nums, 0, nums.length - 1, k);}public static int quickSortFindK(int[] nums, int left, int right, int k) {//选取枢轴元素int pivot = nums[left];int low = left;int high = right;while (low < high) {while (low < high && nums[high] <= pivot)high--;nums[low] = nums[high];while (low < high && nums[low] >= pivot)low++;nums[high] = nums[low];}//low(或者right)就是这趟排序中枢轴元素的最终位置nums[low] = pivot;if (low == k - 1) {return pivot;} else if (low > k - 1) {return quickSortFindK(nums, left, low - 1, k);} else {return quickSortFindK(nums, low + 1, right, k);}}
} 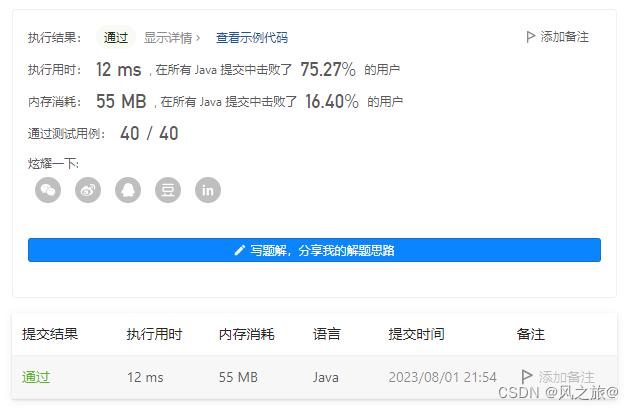
快速排序的最好时间复杂度是O(nlogn),最坏时间复杂度为O(n^2),平均时间复杂度为O(nlogn)
快速排序在元素有序的情况下效率是最低。
不过可以通过在某些情况下,快速排序可以达到期望为线性的时间复杂度,即O(n),也就是在每次排序前随机的交换两个元素(个人理解可能是为了让元素变乱,不那么有序,越乱越快,算法导论中在9.2 期望为线性的选择算法进行了证明,还没有学习,先在此记录下),它的时间代价的期望是 O(n)
具体代码实现,就是在排序前,加上下面的代码
//随机生成一个位置,该位置的范围为[left,right]
//然后将该位置的元素与最后一个元素进行交换,让数组变得不那么有序,
//放置出现有序的情况下快排的时间复杂度退化为o(n^2)
int randomIndex = random.nextInt(right - left + 1) + left;
int tem = nums[randomIndex];
nums[randomIndex] = nums[right];
nums[right] = tem;AC代码:
class Solution {static Random random = new Random();public static int findKthLargest(int[] nums, int k) {return quickSortFindK(nums, 0, nums.length - 1, k);}public static int quickSortFindK(int[] nums, int left, int right, int k) {int randomIndex = random.nextInt(right - left + 1) + left;int tem = nums[randomIndex];nums[randomIndex] = nums[right];nums[right] = tem;int pivot = nums[left];int low = left;int high = right;while (low < high) {while (low < high && nums[high] <= pivot)high--;nums[low] = nums[high];while (low < high && nums[low] >= pivot)low++;nums[high] = nums[low];}nums[low] = pivot;if (low == k - 1) {return pivot;} else if (low > k - 1) {return quickSortFindK(nums, left, low - 1, k);} else {return quickSortFindK(nums, low + 1, right, k);}}
}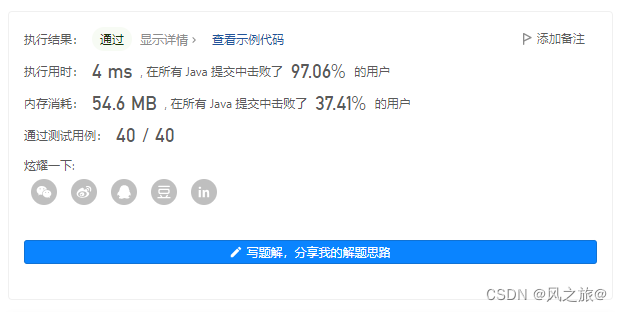
时间上确实有了一些提升
解法二:堆排序。
建立小根堆,最后让小根堆里的元素个数保持在k个,那么此时栈顶的元素就是k个元素中最小的,即第k大的元素
可以通过优先级队列来模拟小根堆
AC代码
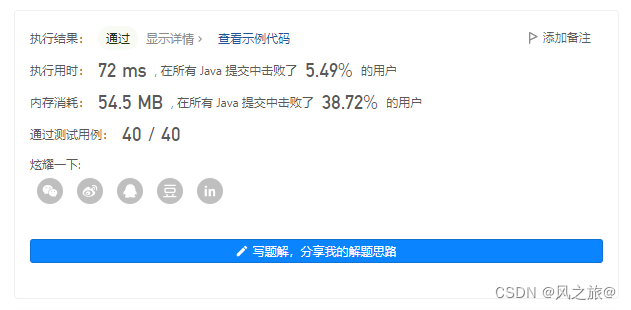
class Solution {public int findKthLargest(int[] nums, int k) {PriorityQueue<Integer> queue = new PriorityQueue<>();for (int num : nums) {//已经有k个元素了,当前元素比堆顶元素还小,不可能是第k大的元素,跳过if (queue.size()==k&&queue.peek()>=num){continue;}queue.offer(num);}while (queue.size()>k){queue.poll();}return queue.peek();}
}
解法三:大根堆
- 对于区间[0,n]建立大根堆后,此时堆顶元素nums[0]为最大值,可以将堆顶元素与最后一个元素交换,即将最大值移动到数组最后,
- 然后将[0,n-1]区间调整为大根堆,此时堆顶nums[0]就是第二大的值,将堆顶元素与倒数第二个元素交换,即倒数第二大的值移动到数组倒数第二个位置
- 然后将[0,n-2]区间调整为大根堆...
- 调整 k-1此后的大根堆,此时的堆顶元素就是第k大的元素
大根堆可以使用优先级队列实现,传递一个降序的比较器。
这里复习下堆排序,手动写了一个大根堆
AC代码:
class Solution {public static int findKthLargest(int[] nums, int k) {createHeap(nums);for (int i = nums.length - 1; i > nums.length - k; i--) {int tem = nums[0];nums[0] = nums[i];nums[i] = tem;heapAdjust(nums, 0, i - 1);}return nums[0];}//建初堆public static void createHeap(int[] nums) {for (int i = nums.length / 2 - 1; i >= 0; i--) {heapAdjust(nums, i, nums.length-1);}}/*调整成大根堆nums[begin+1,end]已经是大根堆,将nums[begin,end]调整为以nums[begin]为根的大根堆*/public static void heapAdjust(int[] nums, int begin, int end) {int tem = nums[begin];for (int i = 2 * begin + 1; i <= end; i = i * 2 + 1) {if (i+1 <= end && nums[i] < nums[i+1])//j为左右子树中较大的子树的下标i++;//tem大于左右子树,已经是大根堆,退出if (tem >= nums[i])break;nums[begin] = nums[i];//更新待插入的位置begin = i;}//tem应该存放的位置nums[begin] = tem;}
}
相关文章:

215. 数组中的第K个最大元素(快排+大根堆+小根堆)
题目链接:力扣 解题思路: 方法一:基于快速排序 因为题目中只需要找到第k大的元素,而快速排序中,每一趟排序都可以确定一个最终元素的位置。 当使用快速排序对数组进行降序排序时,那么如果有一趟排序过程…...

Ubuntu18.04配置ZED_SDK 4.0, 安装Nvidia显卡驱动、cuda12.1
卸载错误的显卡驱动、cuda 首先卸载nvidia相关的、卸载cuda sudo apt-get purge nvidia* sudo apt-get autoremove sudo apt-get remove --auto remove nvidia-cuda-toolkit sudo apt-get purge nvidia-cuda-toolkit 官方卸载cuda的方法: sudo apt-get --purge re…...

张量Tensor 深度学习
1 张量的定义 张量tensor理论是数学的一个分支学科,在力学中有重要的应用。张量这一术语源于力学,最初是用来表示弹性介质中各点应力状态的,后来张量理论发展成为力学和物理学的一个有力数学工具。 张量(Tensor)是一个…...

用Rust实现23种设计模式之桥接模式
桥接模式的优点: 桥接模式的设计目标是将抽象部分和实现部分分离,使它们可以独立变化。这种分离有以下几个优点: 解耦和灵活性:桥接模式可以将抽象部分和实现部分解耦,使它们可以独立地变化。这样,对于抽象…...
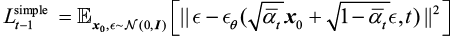
扩散模型实战(一):基本原理介绍
扩散模型(Diffusion Model)是⼀类⼗分先进的基于物理热⼒学中的扩散思想的深度学习⽣成模型,主要包括前向扩散和反向扩散两个过程。⽣成模型除了扩散模型之外,还有出现较早的VAE(Variational Auto-Encoder,…...

解决npm ERR! code ERESOLVE -npm ERR! ERESOLVE could not resolve
当使用一份vue源码开发项目时,npm install 报错了 npm ERR! code ERESOLVEnpm ERR! ERESOLVE could not resolvenpm ERR!npm ERR! While resolving: vue-admin-template4.4.0npm ERR! Found: webpack4.46.0npm ERR! node_modules/webpacknpm ERR! webpack"^4.0…...
HttpServletRequest和HttpServletResponse的获取与使用
相关笔记:【JavaWeb之Servlet】 文章目录 1、Servlet复习2、HttpServletRequest的使用3、HttpServletResponse的使用4、获取HttpServletRequest和HttpServletResponse 1、Servlet复习 Servlet是JavaWeb的三大组件之一: ServletFilter 过滤器Listener 监…...
css在线代码生成器
这里收集了许多有意思的css效果在线代码生成器适合每一位前端开发者 布局,效果类: 网格生成器https://cssgrid-generator.netlify.app/ CSS Grid Generator可帮助开发人员使用CSS Grid创建复杂的网格布局。网格布局是创建Web页面的灵活和响应式设计的强…...
在java中如何使用openOffice进行格式转换,word,excel,ppt,pdf互相转换
1.首先需要下载并安装openOffice,下载地址为: Apache OpenOffice download | SourceForge.net 2.安装后,可以测试下是否可用; 3.build.gradle中引入依赖: implementation group: com.artofsolving, name: jodconverter, version:…...
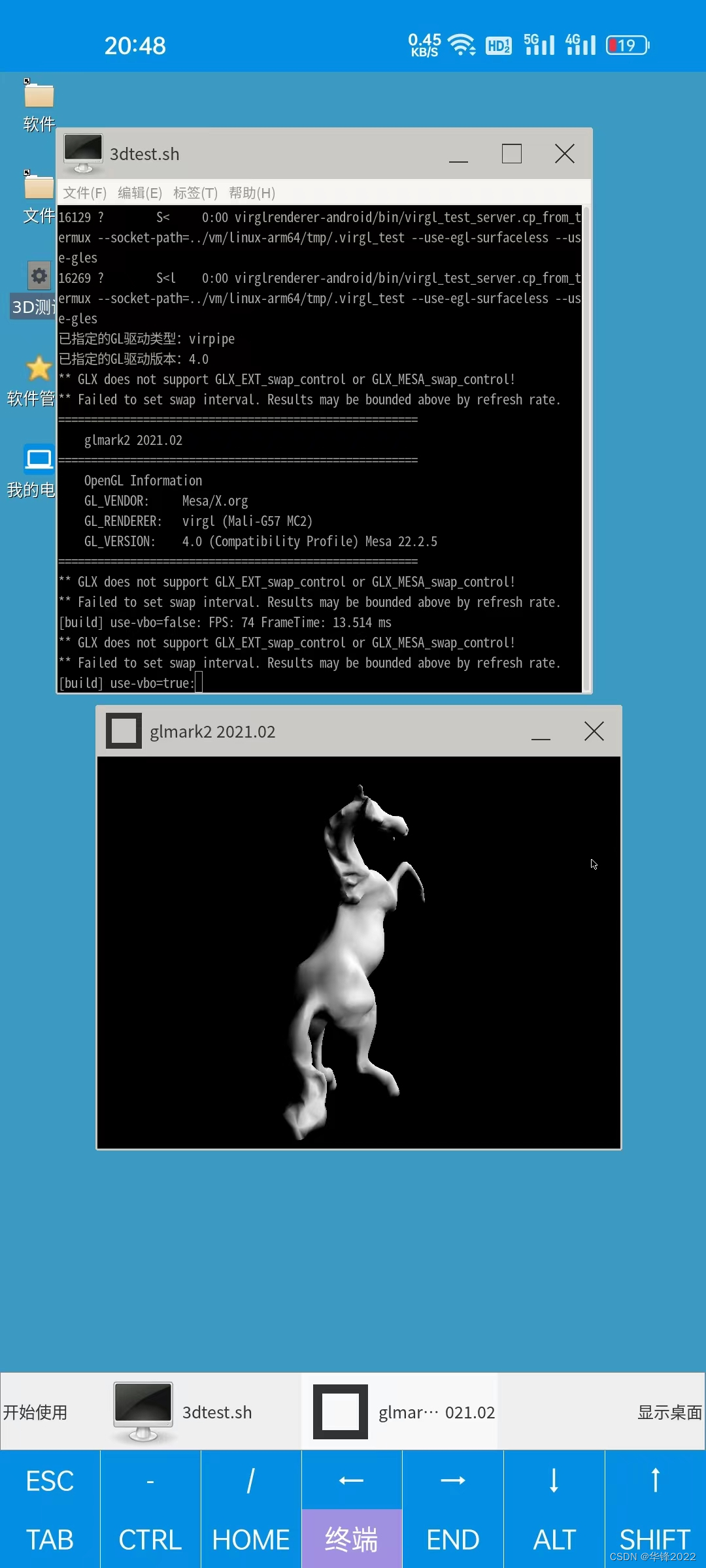
手机变电脑2023之虚拟电脑droidvm
手机这么大的内存,装个app来模拟linux,还是没问题的。 app 装好后,手指点几下确定按钮,等几分钟就能把linux桌面环境安装好。 不需要敲指令, 不需要对手机刷机, 不需要特殊权限, 不需要找驱…...

HDFS中的sequence file
sequence file序列化文件 介绍优缺点格式未压缩格式基于record压缩格式基于block压缩格式 介绍 sequence file是hadoop提供的一种二进制文件存储格式一条数据称之为record(记录),底层直接以<key, value>键值对形式序列化到文件中 优…...
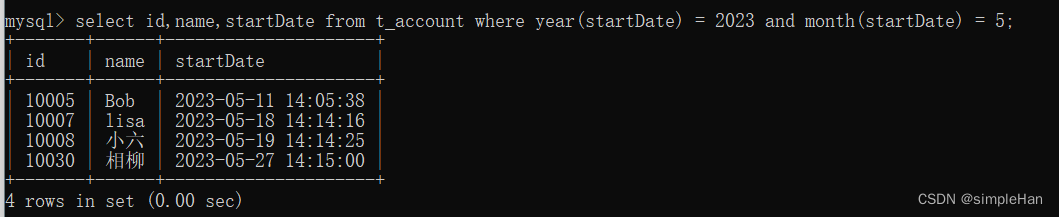
【MySQL】检索数据使用数据处理函数
函数 与其他大多数计算机语言一样,SQL支持利用函数来处理数据。函数一般是在数据上执行的,它给数据的转换和处理提供了方便。 函数没有SQL的可移植性强:能运行在多个系统上的代码称为可移植的。多数SQL语句是可移植的,而函数的可…...

【嵌入式学习笔记】嵌入式入门6——定时器TIMER
1.定时器概述 1.1.软件定时原理 使用纯软件(CPU死等)的方式实现定时(延时)功能有诸多缺点,如CPU死等、延时不精准。 void delay_us(uint32_t us) {us * 72;while(us--); }1.2.定时器定时原理 使用精准的时基&#…...
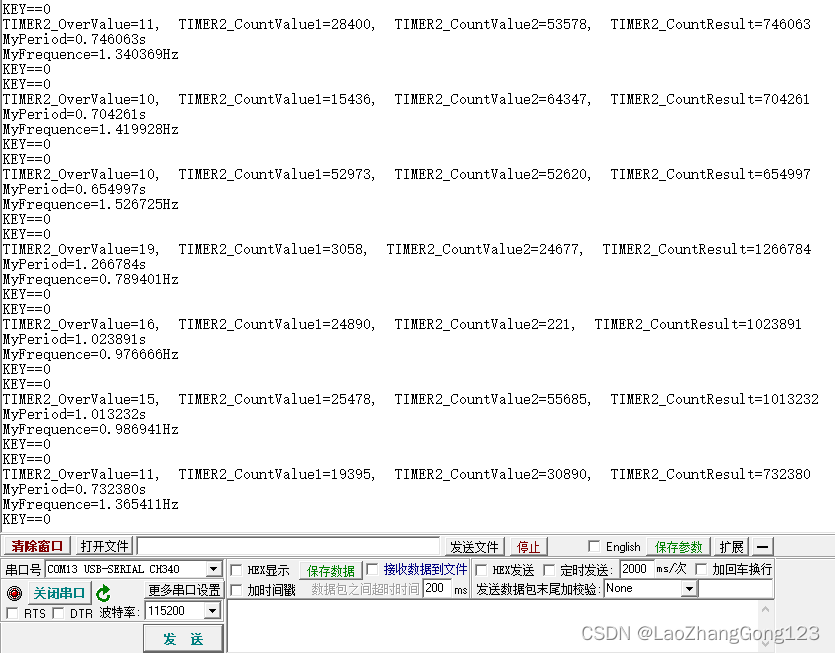
GD32F103输入捕获
GD32F103输入捕获程序,经过多次测试,终于完成了。本程序将TIMER2_CH2通道映射到PB0引脚,捕获PB0引脚低电平脉冲时间宽度。PB0是一个按钮,第1次按下采集一个值保存到TIMER2_CountValue1中,第2次按下采集一个值保存到TIM…...
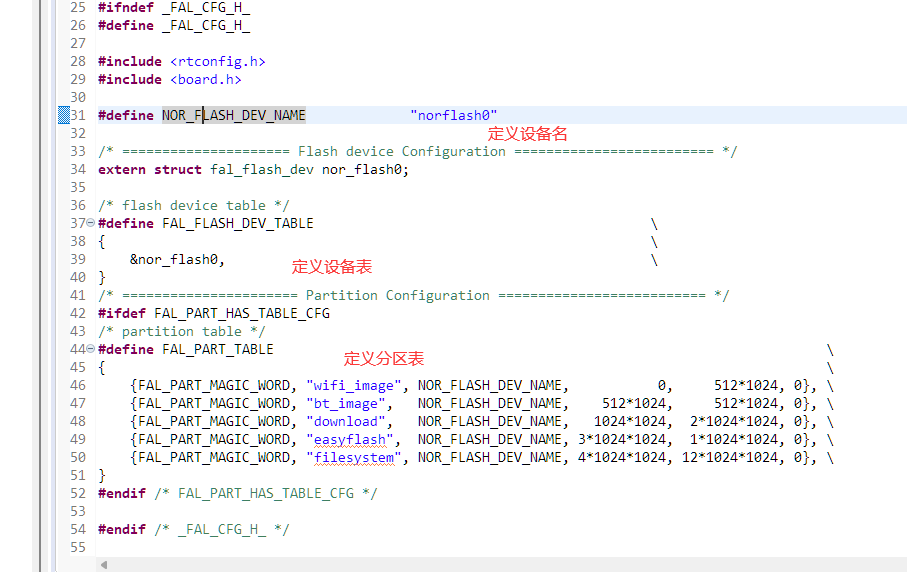
[RT-Thread]基于ARTPI的文件系统认识与搭建
[写作为了记忆,个人最终输出的内容往往是遗忘后最容易捡起的内容,故以此作文] 目录 [写作为了记忆,个人最终输出的内容往往是遗忘后最容易捡起的内容,故以此作文] 前提 内容 认识 基于ARTPI的文件系统的挂载 ROMFS与LFS. (默认自动挂载,romfs可读不可写) 搭…...

动态规划+二分查找
题目描述:给定一个区间数组,[[1,2,3],[3,4,2],[2,4,4]],每个区间有价值,求在获取k个区间的条件下面,求获得的最大的价值,关键是dp的定义和二分查找的写法(小于tar额最右下标) import…...

8.2小非农ADP数据来袭黄金将会如何表现?
近期有哪些消息面影响黄金走势?黄金多空该如何研判? 黄金消息面解析: 周二(8月1日)现货黄金价格回落,原因是美元指数升创7月10日以来新高至102.43.美联储官员乐观言论夯实美国经济软着陆预期。此外,中国刺激措施将…...

linux启动oracle
一、启动方法 方法1: Sql代码 cd $ORACLE_HOME/bin #进入到oracle的安装目录 ./dbstart #重启服务器 ./lsnrctl start #重启监听器 ----------------------------------- 方法2: (1) 以oracle身份登录数据库&am…...

AssetBundleBrowser导入报错解决方案
第一次导入AssetBundleBrowser遇到报错有 Assets\Scenes\AssetBundles-Browser-master\AssetBundles-Browser-master\Tests\Editor\ABModelTests.cs(13,7): error CS0246: The type or namespace name Boo could not be found (are you missing a using directive or an assem…...
vue-baidu-map-3x 使用记录
在 Vue3 TypeScript 项目中,为了采用 标签组件 的方式,使用百度地图组件,冲浪发现了一个开源库 ovo,很方便!喜欢的朋友记得帮 原作者 点下 star ~ vue-baidu-map-3xbaidu-map的vue3/vue2版本(支持v2.0、v…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
